Методом линейного программирования, целочисленного программирования
методом ветвей и границ, симплекс-методом, транспортная задача,
задача по оптимизации производства
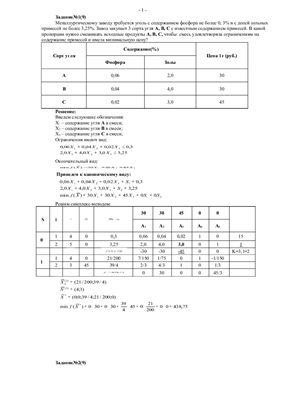
1. Металлургическому заводу требуется уголь с содержанием фосфора не более 0, 3% и с долей зольных примесей не более 3,25%. Завод закупает 3 сорта угля А, В, С с известным содержанием примесей. В какой пропорции нужно смешивать исходные продукты А, В, С, чтобы смесь удовлетворяла ограничениям на содержание примесей и имела минимальную цену?
2. Предприятие производит три вида продукции А1, А2, А3, используя сырье двух видов: В1 и В
2. Известны затраты сырья i-го вида на единицу изделия j-го вида aij, количество сырья каждого вида bi (i=1,2), а так же прибыль полученная от единицы изделия j-го вида сj (j=1,2,3). Сколько изделий каждого вида необходимо произвести, что бы получить: max прибыли; max товарной продукции.
3. Предприятию необходимо выпустить по плану продуции А1 – 500 единиц, А2 – 300, А3 –
450. Каждый вид изделия может производиться на двух машинах. Полезное затрачиваемое время каждой машины 5000 мин. Как распределить работу машин, чтобы общие затраты времени на выполнение плана были минимальными, если задана матрица затрат. Учитывать возможность перевыполнение плана.
4. Из четырех видов кормов необходимо составить рацион, в состав которого должно входить не менее В1 единиц вещества А, В2 единиц вещества В и В3 единиц вещества С. Количество единиц вещества, содержащегося в одном килограмме каждого вида, указано в таблице. В ней же приведена цена одного кг. корма каждого вида.
Составить рацион, содержащий не менее нужного количества указанных питательных веществ и имеющих минимальную стоимость.
5. Решить задачи двухэтапным симплекс-методом без учета возможности перевыполнения плана. Предприятию необходимо выпустить по плану продуции А1 – 500 единиц, А2 – 300, А3 –
450. Каждый вид изделия может производиться на двух машинах. Полезное затрачиваемое время каждой машины 5000 мин. Как распределить работу машин, чтобы общие затраты времени на выполнение плана были минимальными, если задана матрица затрат. Учитывать возможность перевыполнение плана.
6. Решить задачу целочисленного программирования методом ветвей и границ, учитывая цело численность переменных.
1. Металлургическому заводу требуется уголь с содержанием фосфора не более 0, 3% и с долей зольных примесей не более 3,25%. Завод закупает 3 сорта угля А, В, С с известным содержанием примесей. В какой пропорции нужно смешивать исходные продукты А, В, С, чтобы смесь удовлетворяла ограничениям на содержание примесей и имела минимальную цену?
2. Предприятие производит три вида продукции А1, А2, А3, используя сырье двух видов: В1 и В
2. Известны затраты сырья i-го вида на единицу изделия j-го вида aij, количество сырья каждого вида bi (i=1,2), а так же прибыль полученная от единицы изделия j-го вида сj (j=1,2,3). Сколько изделий каждого вида необходимо произвести, что бы получить: max прибыли; max товарной продукции.
3. Предприятию необходимо выпустить по плану продуции А1 – 500 единиц, А2 – 300, А3 –
450. Каждый вид изделия может производиться на двух машинах. Полезное затрачиваемое время каждой машины 5000 мин. Как распределить работу машин, чтобы общие затраты времени на выполнение плана были минимальными, если задана матрица затрат. Учитывать возможность перевыполнение плана.
4. Из четырех видов кормов необходимо составить рацион, в состав которого должно входить не менее В1 единиц вещества А, В2 единиц вещества В и В3 единиц вещества С. Количество единиц вещества, содержащегося в одном килограмме каждого вида, указано в таблице. В ней же приведена цена одного кг. корма каждого вида.
Составить рацион, содержащий не менее нужного количества указанных питательных веществ и имеющих минимальную стоимость.
5. Решить задачи двухэтапным симплекс-методом без учета возможности перевыполнения плана. Предприятию необходимо выпустить по плану продуции А1 – 500 единиц, А2 – 300, А3 –
450. Каждый вид изделия может производиться на двух машинах. Полезное затрачиваемое время каждой машины 5000 мин. Как распределить работу машин, чтобы общие затраты времени на выполнение плана были минимальными, если задана матрица затрат. Учитывать возможность перевыполнение плана.
6. Решить задачу целочисленного программирования методом ветвей и границ, учитывая цело численность переменных.