220 стр. Представлены лекции профессора, доктора
физико-математических наук, зав. кафедрой высшей математика
Белорусского государственного экономического университета М. П.
Дымкова.
Содержание:
Основные теоремы дифференциального исчисления.
Формулы Маклорена и Тейлора.
Разложение в ряд Маклорена элементарных функций.
Исследование функций с помощью производных.
Функции многих переменных.
Неопределенный интеграл.
Определенный интеграл.
Геометрические приложения определенного интеграла.
Двойные интегралы.
Примера задач, приводящие к дифференциальными уравнениям.
Комплексные числа.
Линейные дифференциальные уравнения 1-го порядка.
Линейные дифференциальные уравнения 2-го порядка.
Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
Понятие устойчивости решений ДУ.
Ряды (примеры и решения).
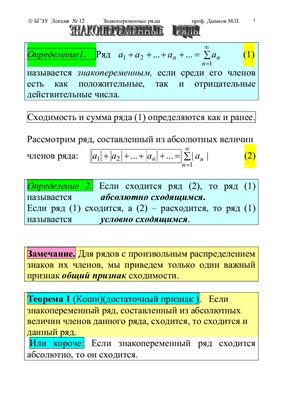
Ряды. Знакопеременные ряды (примеры и решения).
Разложение обратных тригонометрических функций в степенные ряды.
Содержание:
Основные теоремы дифференциального исчисления.
Формулы Маклорена и Тейлора.
Разложение в ряд Маклорена элементарных функций.
Исследование функций с помощью производных.
Функции многих переменных.
Неопределенный интеграл.
Определенный интеграл.
Геометрические приложения определенного интеграла.
Двойные интегралы.
Примера задач, приводящие к дифференциальными уравнениям.
Комплексные числа.
Линейные дифференциальные уравнения 1-го порядка.
Линейные дифференциальные уравнения 2-го порядка.
Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
Понятие устойчивости решений ДУ.
Ряды (примеры и решения).
Ряды. Знакопеременные ряды (примеры и решения).
Разложение обратных тригонометрических функций в степенные ряды.