Владыкина Н.Д., Ермаков А.И., Курчанова С.С., Хмеленко Г.И. Методич. указания по курсу высшей математики. Часть 1
Подождите немного. Документ загружается.

УДК 517
Методические указания по курсу высшей математики: линейная алгебра,
аналитическая геометрия, дифференциальное исчисление функций одной
переменной (для студентов заочного отделения экономических и технических
специальностей)
/Сост. Н.Д. Владыкина, А.И. Ермаков, С.С. Курчанова, Г.И. Хмеленко. –
Луганск: изд. Восточноукр. Нац. ун-та им. В. Даля, 2002. - 100 стр.
Методические указания содержат примеры решения типовых задач
контрольной работы по высшей математике и варианты самой контрольной
работы.
Составители: Н. Д. Владыкина, асс.
А.И. Ермаков, доц.
С.С. Курчанова, асс.
Г.И. Хмеленко, ст. преп.
Рецензент Кучма В. Я., доц.
Ответственный Ю. М. Арлинский, проф.
за выпуск
1
Курс высшей математики можно освоить только при активном решении
задач. Особенно это касается техники дифференцирования и интегрирования
функций, решения дифференциальных уравнений. В процессе
самостоятельного выполнения семестровой работы студенту необходимо
изучить теоретический материал, способствующий осмысленному решению
задач. Полезно и эффективно после выполнения контрольной работы еще раз
вернуться к изучению теории с целью ее более глубоко усвоения, осознания
взаимосвязи основных фактов и теорем. У студентов заочной формы обучения
меньше возможностей (во времени) непосредственного общения с
преподавателем. Методические указания и призваны восполнить этот
недостаток общения. Конечно, без хорошего учебника не обойтись. Их много.
Наиболее популярные и рекомендуемые следующие:
1. Д. В. Беклемишев. Курс аналитической геометрии и линейной алгебры.
– М.: Наука, 1984
2. В. А. Ильин, Э. В. Позняк. Аналитическая геометрия. – М.: Наука, 1981
3. В. А. Ильин, Э. В. Позняк. Линейная алгебра. – М.: Наука, 1984
4. А. І. Єрмаков, М. М. Крамар. Лінійна алгебра. – Л.: СУДУ, 2000
5. В. В. Пак, Ю. Л. Носенко. Высшая математика. – Д.: Сталкер, 1987
6. Н. С. Пискунов. Дифференциальное и интегральное исчисления для
вузов, т. 1. – М.: Наука, 1985
7. Высшая математика для экономистов. Под редакцией проф. Н. Ш.
Крамера. – М.: «Биржи и банки», 1997
8. П. Е. Данко, А. Г. Попов, Т. Л. Кожевникова. Высшая математика в
упражнениях и задачах. В 2-х ч. – М.: Высш. Шк., 1986
2
Программа
для подготовки к экзамену по математике
(I семестр)
1. Матрицы. Основные понятия. Линейные операции над матрицами.
2. Умножение матриц.
3. Обратная матрица.
4. Определители, их вычисление и свойства.
5. Миноры. Алгебраические дополнения. Теорема Лапласа о разложении
определителя по строке (столбцу).
6. Ранг матрицы. Элементарные преобразования матриц. Теоремы о ранге
матрицы.
7. Системы линейных уравнений. Теорема Крамера.
8. Решение систем линейных уравнений методом обратной матрицы.
9. Метод Гаусса.
10. Система m линейных уравнений с n неизвестными. Теорема Кронекера-
Капелли.
11. Системы линейных однородных уравнений. Фундаментальная система
решений.
12. Векторы. Действия над векторами: сложение, вычитание, умножение на
число.
13. Скалярное произведение векторов.
14. Векторное произведение векторов.
15. Смешанное произведение векторов.
16. Линейное пространство. Основные понятия и определения. Размерность.
Базис.
17. Переход к новому базису в линейном пространстве.
18. Евклидово пространство. Ортонормированный базис в евклидовом
пространстве.
19. Линейные операторы.
20. Собственные векторы и собственные значения линейного оператора.
21. Квадратичные формы. Приведение к каноническому виду.
22. Виды уравнений прямой на плоскости.
23. Условия параллельности и перпендикулярности прямых на плоскости.
Расстояние от точки до прямой.
24. Окружность и эллипс.
25. Гипербола.
26. Парабола.
27. Уравнение прямой в пространстве.
28. Уравнение плоскости. Расстояние от точки до плоскости.
29. Взаимное расположение прямой и плоскости.
30. Поверхности второго порядка.
31. Основные понятия теории множеств.
3
32. Понятие функции. Основные свойства функций.
33. Элементарные функции. Классификация функций.
34. Предел числовой последовательности. Предел функции в точке и в
бесконечности.
35. Бесконечно малые и бесконечно большие величины и связь между ними.
36. Основные теоремы о пределах. Признаки существования предела.
37. Первый и второй замечательные пределы.
38. Непрерывность функций. Свойства функций, непрерывных в точке и на
отрезке.
39. Задачи, приводящие к понятию производной. Определение производной.
40. Основные правила дифференцирования.
41. Производная сложной и обратной функций.
42. Производная неявной функции и функции, заданной параметрически.
43. Производные основных элементарных функций. Таблица производных.
44. Производные высших порядков.
45. Теоремы Ферма, Роля, Лагранжа и Коши.
46. Правило Лопиталя.
47. Формула Тейлора.
48. Возрастание и убывание функций. Экстремумы. Наибольшее и
наименьшее значения функции на отрезке.
49. Выпуклость функции. Точки перегиба.
50. Асимптоты графика функции.
51. Дифференциал функции. Его применение к приближенным вычислениям.
52. Понятие о дифференциалах высших порядков.
4
I. Линейная алгебра
Определители
Матрицей размера m x n называется прямоугольная таблица чисел a
ij
, i=1,
2, …, m, j=1, 2, …, n, состоящая из m строк и n столбцов.
А =
mnmm
n
n
aaa
aaa
aaa
...
............
...
...
21
22221
11211
(1)
При m = n матрица называется квадратной. Каждой квадратной матрице
по определённому правилу ставится в соответствие число, называемое
определителем матрицы и обозначаемое
| A | =
mnmm
n
n
aaa
aaa
aaa
...
............
...
...
21
22221
11211
При n = 2 по определению
| A | =
2221
1211
aa
aa
=
21122211
aaaa
.
При вычислении определителей порядка выше второго применяют
свойства, которые формулируются ниже.
1. Величина определителя не изменится, если все его строки заменить
столбцами с тем же номером, т.е.
.
332313
322212
312111
333231
232221
131211
aaa
aaa
aaa
aaa
aaa
aaa
2. Перестановка двух столбцов или двух строк определителя равносильна
умножению его на –1.
3. Если определитель имеет два одинаковых столбца или строки, то он равен
нулю.
4. Умножение всех элементов одного столбца или одной строки
определителя на любое число k равносильно умножению определителя на это
число k.
5
5. Если все элементы некоторой строки или столбца равны нулю, то сам
определитель равен нулю.
6. Если соответствующие элементы двух столбцов или двух строк
определителя пропорциональны, то сам определитель равен нулю.
7. Если каждый элемент k-го столбца или k-й строки определителя
представляет собой сумму двух слагаемых, то определитель может быть
представлен в виде суммы двух определителей, из которых один в k-м столбце
или соответственно в k-й строке имеет первые из упомянутых слагаемых, а
другой – вторые, элементы, стоящие на остальных местах, у всех трех
определителей одни и те же.
8. Если к элементам некоторого столбца (или некоторой строки) прибавить
соответствующие элементы другого столбца (или строки), умноженные на
любой общий множитель, то величина определителя не изменится.
Минором M
ij
элемента a
ij
называется определитель, получаемый из
данного определителя путем вычеркивания i-ой строки и j-ого столбца, на
пересечении которых расположен этот элемент.
Алгебраическим дополнением элемента a
ij
называется минор этого
элемента, взятый со своим знаком, если сумма номеров строки и столбца, на
пересечении которых расположен элемент, есть число четное, и с
противоположным знаком, если это число нечетное, т.е.
A
ij
= (-1)
i+j
M
ij
.
9. Определитель равен сумме произведений элементов какого-либо столбца
(или строки) на их алгебраические дополнения, т.е.:
|A| =
=
3
1
3,2,1,
j
ijij
iAa
или
3
1
,
ij ij
i
a A
3,2,1j
.
Пример:
11
1 1
1 2 4 1 2 1( 2) 4 1( 4) 1 0 0
2 3 3 2 3 2( 2) 3 2( 4) 2 1 5 1
3 1 2 3 1 3( 2) 2 3( 4) 3 5 10
1 5 1 5 1 1
( 1) 5 5(2 5) 15.
5 10 5 10 5 2
A
При решении использованы 8-е и 9-е свойства определителей.
Проверим результат вычисления, действуя иначе:
6
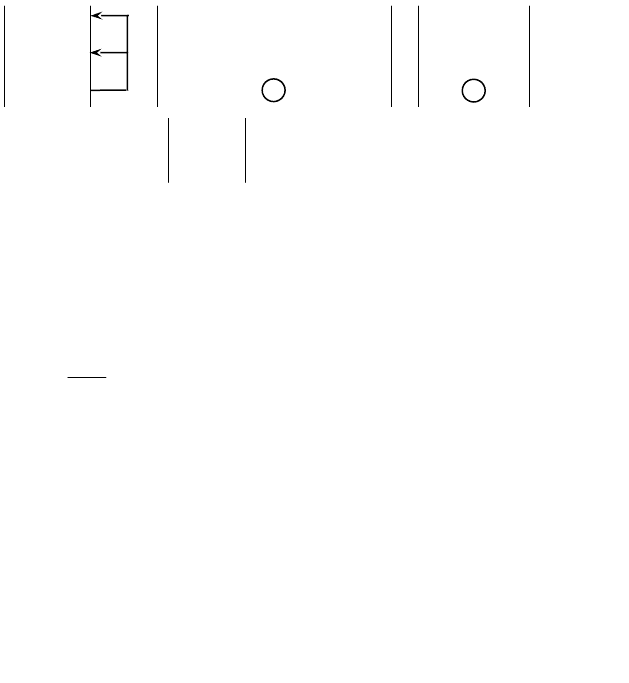
( 2)
( 3) 32
3 2
32
1 2 4 1 3( 2) 0 4 2( 2) 5 0 0
2 3 3 2 3( 3) 0 3 2( 3) 7 0 3 1
3 1 2 3 1 2 3 1 2
5 0
( 1) (15 7 0) 15.
7 3
A
M
Обратная матрица
Для квадратной невырожденной матрицы А, т.е. при |A|
0, существует
обратная матрица, вычисляемая по формуле:
nnnn
n
n
AAA
AAA
AAA
A
A
...
............
...
...
||
1
21
22212
12111
1
. Для неё A
-1
A = AA
-1
= E, где: E=
100
010
001
- единичная матрица.
Пример: Найти обратную матрицу для матрицы:
213
332
421
A
.
Решение: Так как |A|=-15
0, то матрица A невырожденная и для нее
существует обратная матрица A
-1
. Вычислим алгебраические дополнения
элементов a
ij
матрицы А по формуле A
ij
= (-1)
i+j
M
ij
.
7
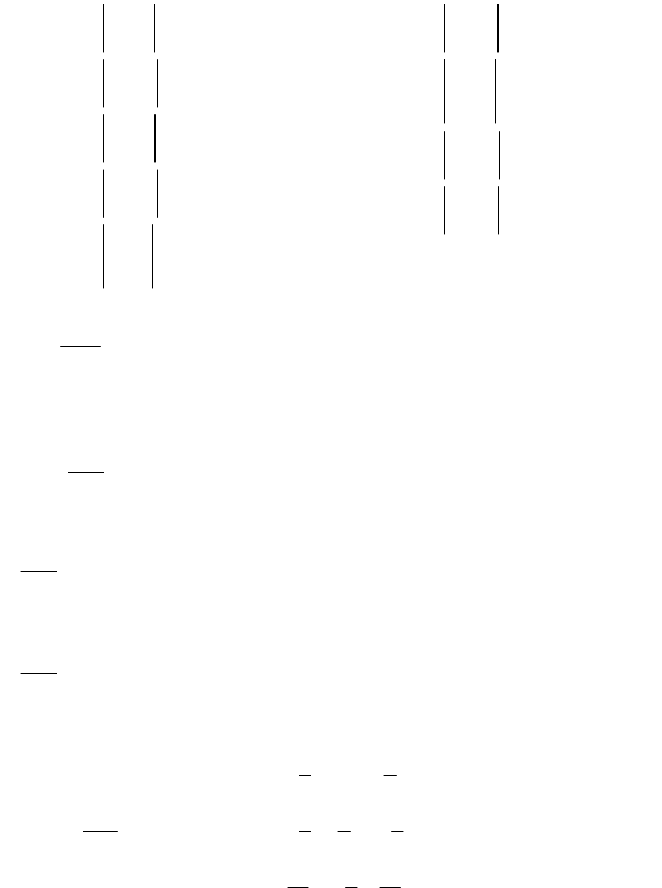
A
11
= (-1)
1+1
336
21
33
.
A
12
= (-1)
1+2
5)94(
23
32
.
A
13
= (-1)
1+3
792
13
32
.
A
21
= (-1)
2+1
0)44(
21
42
.
A
22
= (-1)
2+2
1 4
2 12 10
3 2
.
A
23
= (-1)
2+3
5)61(
13
21
.
A
31
= (-1)
3+1
2 4
6 12 6
3 3
.
A
32
= (-1)
3+2
5)83(
32
41
.
A
33
= (-1)
3+3
143
32
21
.
1
3 0 6
1
5 10 5
15
7 5 1
A
.
Убедимся в правильности вычислений: покажем, что A
-1
A = E.
1
3 0 6 1 2 4
1
5 10 5 2 3 3
15
7 5 1 3 1 2
A A
3 1 0 2 ( 6) 3 3 2 0 3 ( 6) 1 3 4 0 3 ( 6) 2
1
5 1 ( 10) 2 5 3 5 2 ( 10) 3 5 1 5 4 ( 10) 3 5 2
15
7 1 5 2 ( 1) 3 7 2 5 3 ( 1) 1 7 4 5 3 ( 1) 2
15 0 0 1 0 0
1
0 15 0 0 1 0
15
0 0 15 0 0 1
E
.
Вычисление выполнено верно:
A
-1
=
1 2
0
5 5
3 0 6
1 1 2 1
5 10 5
15 3 3 3
7 5 1
7 1 1
15 3 15
;
8

Ответ: A
-1
=
1 2
0
5 5
1 2 1
3 3 3
7 1 1
15 3 15
.
Системы линейных алгебраических уравнений
(СЛАУ)
Системы m линейных алгебраических уравнений относительно n
неизвестных x
1
, x
2
, …, x
n
имеют вид
....
...............
,...
,...
2211
22222121
11212111
mnmnmm
nn
nn
bxaxaxa
bxaxaxa
bxaxaxa
(2)
где a
ij
(i=1,2,…,m; j=1,2,…,n) – известные коэффициенты; b
1
, b
2
, …, b
m
–
свободные члены. Решением СЛАУ называется любая совокупность значений
неизвестных x
1
=d
1
, x
2
=d
2
, …, x
n
=d
n
, при подстановке которых все уравнения
СЛАУ обращаются в тождества. СЛАУ называется совместной, если она
имеет по крайней мере одно решение. В противном случае, по определению,
система несовместна.
Метод Крамера
Рассмотрим систему трех уравнений с тремя неизвестными.
.
,
,
3333231
2232221
1131211
bzayaxa
bzayaxa
bzayaxa
Выпишем главный определитель системы
и вспомогательные
определители
zyx
,,
.
9
,
333231
232221
131211
aaa
aaa
aaa
,
33323
23222
13121
aab
aab
aab
x
,
33331
23221
13111
aba
aba
aba
y
33231
22221
11211
baa
baa
baa
z
, тогда
,
x
x
,
y
y
.
z
z
Если
0
, то система имеет единственное решение.
Если
0
, а хотя бы один из
0,,
321
, то в этом случае
система решений не имеет.
Если
0
321
, то система также может совсем не иметь
решений; но если система при этих условиях имеет хотя бы одно решение, то
она имеет бесконечное множество решений.
Однородной системой трех уравнений первой степени с тремя
неизвестными называется система вида:
,0
,0
,0
333232131
323222121
313212111
xaxaxa
xaxaxa
xaxaxa
т.е. система уравнений, свободные члены которой равны нулю.
Однородная система уравнений имеет единственное нулевое решение
при
0
и бесчисленное множество решений при
0
.
Матричный способ решения
(решение с помощью обратной матрицы)
Систему трех уравнений с тремя неизвестными можно представить в
виде матричного уравнения:
AX = B, где
333231
232221
131211
aaa
aaa
aaa
A
,
z
y
x
X
,
3
2
1
b
b
b
B
.
В предположении, что A невырождена, решение этого матричного
уравнения находится умножением обеих его частей на обратную матрицу A
-1
:
A
-1
AX=A
-1
B.
Так как A
-1
A = E, AE=EA=A, то X = A
-1
B.
Пример: Решить систему трех уравнений с тремя неизвестными при
помощи определителей и с помощью обратной матрицы.
10
