Владыкина Н.Д., Ермаков А.И., Курчанова С.С., Хмеленко Г.И. Методич. указания по курсу высшей математики. Часть 1
Подождите немного. Документ загружается.

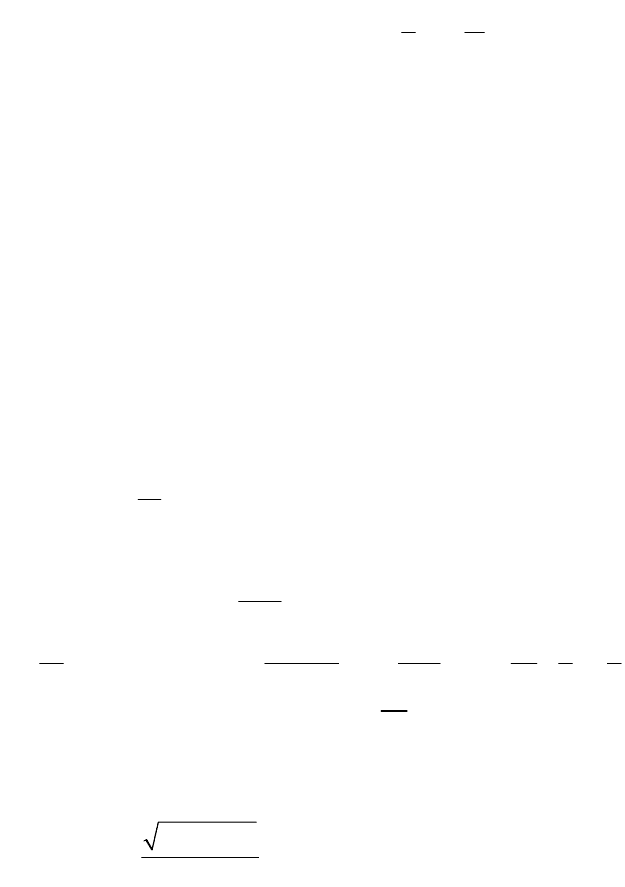
1)Отношение двух функций, каждая из которых стремиться к нулю или
бесконечности (имеет неопределенность вида
0
0
или
);
2)произведения двух функций, одна из которых стремится к нулю, а
другая - к бесконечности (неопределенность вида
0
);
3)разности двух функций, стремящихся к бесконечности
(неопределенность вида
);
4)степенно-показательной функции, основание которой стремится к.
единице, а показатель - к бесконечности (неопределенность вида
1
);
5)суммы функций, число слагаемых которой изменяется с изменением
аргумента.
В этих случаях для отыскания предела необходимо преобразовать
выражение, чтобы избавиться от неопределенности или свести вопрос к
известному случаю.
Рассмотрим некоторые приемы, используемые для вычисления пределов
при наличии неопределенностей.
I. Если выражение, предел которого нужно найти, представляет собой
сумму, число слагаемых которой возрастает с ростом
n
, то предел легко
вычисляется, если удается просуммировать эти слагаемые.
Пример.
Найти:
2
1
1 2 3 ...
n
im
n
n
.
Решение.
Выражение, записанное в скобках, есть сумма членов арифметической
прогрессии
n
n
n
2
1
...21
.
2 2
1
1 1 1 1 1
1 2 3 ...
2 2 2 2 2
n
n
n
n
n n
n
im
im
im
im
n n n n
.
Если в случае неопределенности
числитель и знаменатель
представлены в виде суммы нескольких слагаемых, одно из которых растет
быстрее остальных, то такое слагаемое (главный член суммы) нужно вынести
за скобки.
Пример 3:
Найти:
3
3
2 1
2
n
n n
im
n
.
Решение:
51
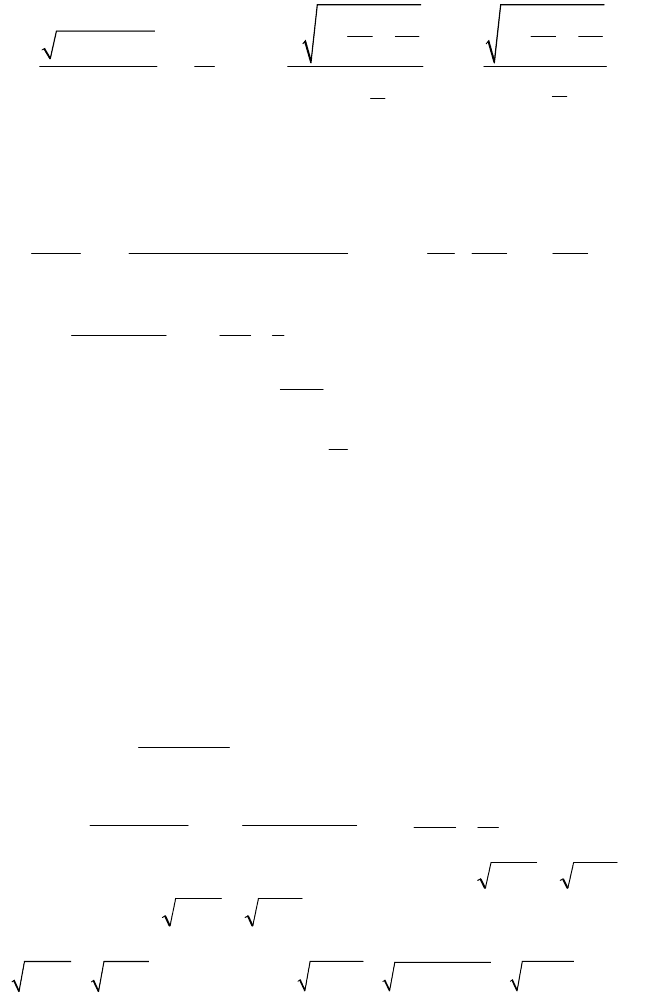
3 3
3
3
2 3 2 3
2 1 2 1
1 1
2 1
lim lim lim 1.
2
2
2
1
1
n n n
n
n n
n n n n
n
n
n
n
Можно также при нахождении таких пределов воспользоваться тем
фактом, что многочлен
n
-й степени от x
1 2
0 1 2
...
n n n
n
Ф x a x a x a x a
эквивалентен своему старшему члену
n
xa
0
при
x
, так как:
1 2
0 0 0 1 2
2
0 0 0 0 0
...
1 ... 1.
n n n
n
n n
n n n
x
x
x
Ф x
a x a x a x a a
a a
im
im
im
a x a x a x a x a x
Пример 4.
2 2
2 2
5 2 5 5
3 4 1 3 3
x
x
x x x
im
im
x x x
.
1. Если требуется найти
0x
f x
im
g x
, причем
0
x a
f x
im
;
0
x a
im
g x
,
то имеет место неопределенность
0
0
. Для вычисления таких пределов
можно использовать следующие примеры:
a) Если
xf
и
xg
- многочлены, имеющие корень
ax
, то в
числителе и знаменателе можно выделить общий множитель
k
x a
наибольшей степени и сократить на него. Сокращение на этот множитель
возможно, т.к. в определении предел функции при
ax
ставится условие
ax
.Выделение множителя
k
x a
осуществить либо путем деления
многочлена на
ax
"в столбик", либо путем группировки слагаемых.
Пример 5.
Найти:
2
2
5
7 10
25
x
x x
im
x
.
Решение:
1)
2
2
5
5
2 5
7 10
25 5 5
x
x
x x
x x
im
im
x x x
5
2 3
5 10
x
x
im
x
;
2)В случае, когда
xf
или
xg
имеет вид
0 xVxU
при
ax
или
0
33
xVxU
при
ax
, то выражение можно
умножить и разделить на сопряженное ему выражение: в первом случае на
U x V x
, во втором на
2 2
3 3
3
U x U x V x V x
.
52

Пример 6.
Найти:
2
7
2 3
49
x
x
im
x
.
Решение:
2
2
7
7
7
2 3 2 3
4 3
2 3
49
49 2 3 7 7 2 3
x
x
x
x x
x
x
im
im
im
x
x x x x x
7 7
7 1 1
.
56
7 7 2 3 7 2 3
x x
x
im im
x x x x x
Пример 7.
Найти
3 3
0h
x h x
im
h
.
Решение:
2
3
2
3 3
3
3
3 3
0
2
0
3 2
3
3
h
h
x h x x h x x h x
x h x
im
im
h
h x h x x h x
0
0
2
2
3 2
3 2
3
3
3
3
3 2
1
1
;
3
h
h
x h x
im
im
x h x x h x
h x h x x h x
x
3)очень удобным средством вычисления пределов отношения и
произведения функций является использование эквивалентных функций:
xsin
~
,x
0x
,
xarcsin
~
,x
0x
,
tgx
~
,x
0x
,
arctgx
~
,x
0x
,
xn 1
~
,x
0x
,
shx
~
,x
0x
,
1
x
e
~
,x
0x
,
thx
~
,x
0x
,
1
x
a
~
ln ,x a
0x
,
xcos1
~
2
,
2
x
0x
.
11
x
~
,x
0x
,
53
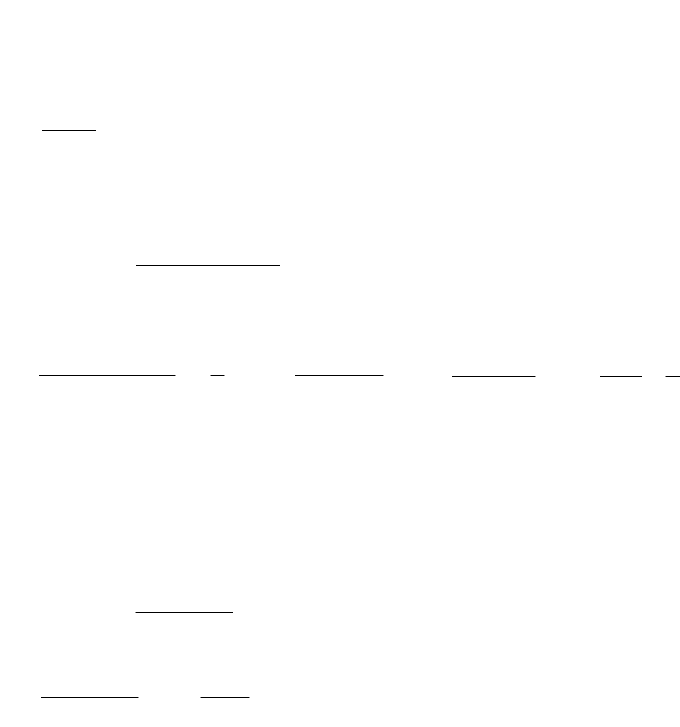
Если
0u x
при
0
xx
, то всюду в этой таблице можно вместо
x
писать
u x
, например,
xusin
~
xu
0
xx
,
0
x x
f x g x
im
,
0
x x
f x
im
g x
не изменяются, если любую из функций
xf
,
xg
заменить
эквивалентной ей функцией при
0
xx
.
Пример 8.
Найти
2
2
2
0
1
1
x
x
x n x x
im
e
.
Решение:
2 2
2
2 2
2
0 0
2
0
0
1
1
0
1 1
.
0
4 4 4
2
1
x x
x
x
x
x n x x x x x
x x
x
im im
im im
x
x
e
(здесь использованы соотношения
un 1
~
u
,
0u
и
1
u
e
~
,u
0 )u
.
Здесь следует помнить, что эквивалентными можно заменять
сомножители, числитель, знаменатель, если они не входят в слагаемые суммы
(разности) под знаком предела.
Пример 9.
Найти
3
sin
.
x u
tgx x
im
x
Неверно было бы делать следующим образом:
3 3
sin
0
x u
x u
tgx x x x
im
im
x x
.
54

Решение
2
3 3 3 3
1
sin 1
sin 1 cos
sin
cos
2
cos cos
1 1
.
2cos 2
x u
x u x u x u
x u
x
x
x
x x
tgx x
x
im
im im im
x x x x x x
im
x
Замена функций эквивалентными им функциями осуществляется обычно
после предварительных преобразований, из которых наиболее типичными
являются:
1. преобразование сумм тригонометрических функций в произведение;
2. замена переменной
tax
, если
ax
, с целью исследовать предел
при
0t
;
3. применение формул приведения для получения синуса иди тангенса
аргумента, стремящегося к нулю;
4. вынесение за скобки одного из слагаемых, чтобы в скобках получилось
выражение вида
1
u
a
, где
0u
;
5. использование основного тождества
eny
ey
для логарифма, в
частности в случае степенно-показательной функции:
v vlnu
u e
(например,
11
nxxx
ex
~
nxx
при
1x
).
Пример 10.
Найти:
xx
x
ee
xx
im
sinsin
0
.
Решение:
0 0
0 0
2sin cos
sin sin
2 2
1
2 cos cos
2 2 2
.
x x
x
x x
x
x x
x x
x x
x x
im im
e e
e e
x x x
im im
e x e
4.Неопределенности вида
и
0
обычно сводят к
неопределенностям
0
0
или
. Для этой цели часто используют
следующие преобразования:
1)приведение к общему знаменателю;
2)вынесение главного слагаемого за скобки;
55

3)умножение и деление на сопряженное выражение;
4)преобразование вида
xf
xf
1
1
.
Пример 11.
Найти:
3
2
1 3
2 8
x
im
x x
.
Решение:
3
2
2 2
1 3 1 3
2 8 2
2 4 2
x x
im
im
x x x
x x x
;
Приводим к общему знаменателю:
2 2
3 3
2
2
4 2 3 2 1
8 8
x
x
x x x x
im
im
x x
.
Пример 12.
Найти
nnim
x
2
.
Решение:
2 ;
x
im n n
Умножим и разделим на сопряженное выражение:
2 2
2
0
2 2
x x
n n n n
im im
n n n n
.
Пример 13.
Найти
x
a
xim
x
sin
.
Решение:
sin
sin 0 ;
1
x x
a
a
x
im x im
x
x
56

Воспользуемся эквивалентностью
usin
~
,u
0u
.
1
x
a
x
im a
x
.
5. В случае, если имеет место неопределенность
1
, для вычисления
предела используют число
x
x
x
ime
1
1
или
x
x
xime
1
1
.
Вычисление предела в случае неопределенности
1
производится по
следующей схеме:
0 0
0 0
1
.
x x x x
im v x nu x im v x u x
v x
v x nu x
x x x x
im u x im e e e
Здесь используется основное тождество для логарифма:
ny
ey
,
которое при
v
uy
дает
v
v nu v nu
u e e
.
Далее в силу непрерывности функции
x
e
имеем:
0
0
x x
im v x nu x
v x nu x
x x
im e e
.
Учитывая условие
1xu
при
0
xx
, делаем замену функции
xnu
эквивалентной бесконечно малой
1xu
в произведении под
знаком предела. Остается найти
0
1
x x
im v x u x
.
Здесь имеем неопределенность
0
, т.к. по условию
xv
, а
1xu
при
0
xx
.
Пример 14.
Найти
2
1
0
2cos
cos
x
x
x
x
im
.
Решение:
2
2
2 2
0
0
2 2 2
0 0 0
1
1 cos
1 cos 1 cos
1
cos2
cos2 cos 2
0 0
3 3
2sin sin 2
cos cos 2
3
2 2 2 2
cos2 cos2 cos 2
2
cos
1
cos 2
.
x
x
x x x
x
x x
im
n im n
x
x
x x
x
x x
x x
x x x x
x x
im im im
x x x x x x
x
im im e e e
x
e e e e
57
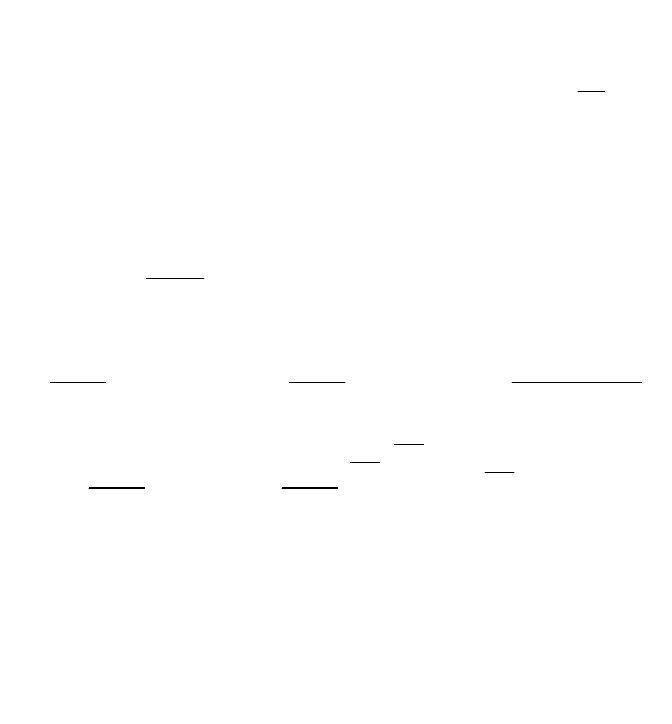
Вычисление предела в случае неопределенности
1
можно проводить
также по следующей схеме:
1
1
0 0 0
0
1
1
1 1 1 1
.
u x
x x
v x u x
v x
v x
x x x x x x
im v x u x
im u x im u x im u x
e
Пример 15.
Найти
2
2
2
5
5
x
x
x
im
x
.
Решение:
2
2 2
2
2
2
2
2
2
2 2 2 2
2 2 2
10
5
5
10
10
10
5
2 2
5 5 5 5
1 1 1 1
5 5 5
10 10
1 1 .
5 5
x
x
x x
x x x
x
x
x
x
x
im
x
x x
x x x x
im im im
x x x
im im e e
x x
При вычислении
xv
xx
xuim
0
встречаются неопределенности вида
0
и
0
0
.
Учитывая, что
xnuxvim
xv
xx
xx
exuim
0
0
, сводим эти
неопределенности к неопределенности
{0 }
в показателе.
58

14. НЕПРЕРЫВНОСТЬ И РАЗРЫВ ФУНКЦИЙ
Если функция
xf
непрерывна в точке
0
x
, то согласно определению
должно выполняться неравенство
0
00
00
xfxfimxfim
xxxx
.
Если в точке
0
x
нарушено хотя бы одно из условий, то
0
x
называется
точкой разрыва функции
xf
. При этом различают следующие случаи:
1)
xfimxfim
xxxx 00
00
, но функция не определена в точке
0
x
. В
этом случае
0
x
называется точкой устранимого разрыва;
2)обе односторонних предела существуют и конечны, но
0 0
0 0x x x x
im f x im f x
. В этом случае
0
x
называется точкой разрыва I
рода (скачок);
3)во всех остальных случаях
0
x
называется точкой разрыва II рода.
Пример 16.
Исследовать на непрерывность функцию
2
,
1,
1.
4 2,
x
при x
f x
при x
x x
Решение:
Так как все основные элементарные функции являются непрерывными
всюду в своей области определения, функция
xxf
1
при
;1x
является непрерывной и функция
24
2
2
xxf
при
1,x
также
является непрерывной. Следовательно, единственной точкой,
«подозрительной» на разрыв, является точка
1x
(точка стыка функции
xf
1
и
xf
2
). Исследуем функцию
xf
на непрерывность в точке
1x
.
1 0 1 0
1.
x x
im f x im x
2
1 0 1 0
2
1
4 2 1;
1 4 2 1.
x x
x
im f x im x x
f x x
Имеем
1 0 1 0
1 .
x x
im f x im f x f
59
Следовательно, точка
1x
является точкой непрерывности функции
xf
. Значит, функция
xf
является непрерывной при всех значениях
;x
.
Пример 17.
Исследовать на непрерывность функцию
x
x
xf
sin
.
Решение:
Числитель и знаменатель дроби определены и непрерывны при всех
значения
;x
.
Точкой, «подозрительной» на разрыв, является точка
0x
, т.к.
функция не определена при
0x
, т.е.
0f
не существует.
1
sinsin
0000
x
x
im
x
x
im
xx
.
Имеем
0 0 0 0x x
im f x im f x
, но
0f
не определена.
Следовательно,
0x
- точка устранимого разрыва функции
xf
т.е., если
функцию доопределить следующим образом
sin
0,
1 0.
x
при x
f x
x
при x
, то
она станет непрерывной при всех значениях
;x
.
Пример 18.
Исследовать на непрерывность функцию
2
2
3 .
x
x
f x
Решение:
Проведя рассуждения, аналогичные приведенным в предыдущих
примерах, определим, что точкой, «подозрительной» не разрыв, является
точка
2x
.
03
2
2
02
x
x
x
im
, т.к.
02 x
, при
02 x
,
2
2
x
x
, при
02 x
.
Аналогично
2
2
02
3
x
x
x
im
,
0f
не определена.
Имеем третий случай, т.е. точка
2x
является точкой разрыва II рода.
60
