Владыкина Н.Д., Ермаков А.И., Курчанова С.С., Хмеленко Г.И. Методич. указания по курсу высшей математики. Часть 1
Подождите немного. Документ загружается.

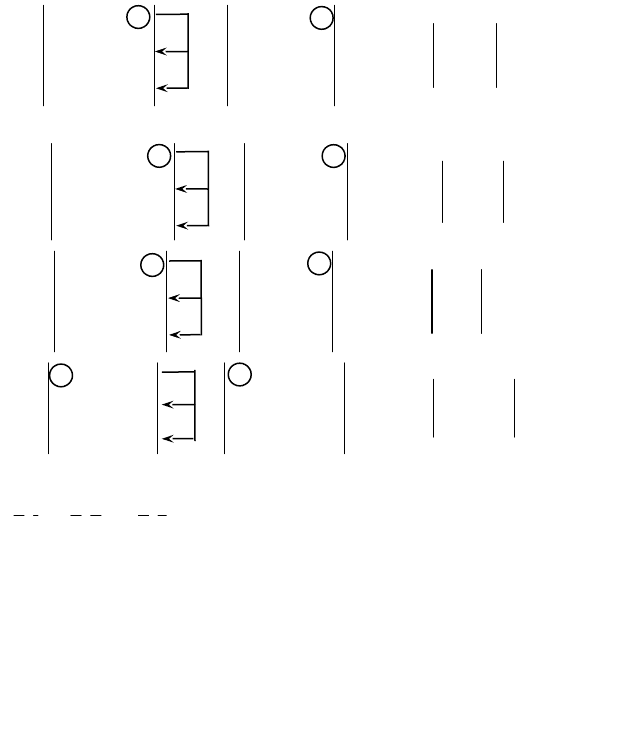
.2233
,72
,4
zyx
zyx
zyx
Решение.
Метод Крамера. Для решения системы найдем главный и побочные
определители:
4
( 1)
2
1 1 1 1 2 1
1 2
2 1 1 1 2 0 1 ( 1) 1 10 9
5 1
3 3 2 5 1 0
.
Так как
0
, система имеет единственное решение.
4
( 1)
2
4 1 1 4 1 1
3 2
7 1 1 3 2 0 1 ( 1) 3 12 9
6 1
2 3 2 6 1 0
x
,
4
( 1)
2
1 4 1 1 4 1
1 3
2 7 1 1 3 0 1 ( 1) 6 15 9
5 6
3 2 2 5 6 0
y
,
2
( 2)
( 3)
1 1 4 1 2 1
3 1
2 1 7 0 3 1 1 ( 1) 42 6 36
6 14
3 3 2 0 6 14
z
По правилу Крамера
4
9
36
;1
9
9
;1
9
9
z
y
x
zyx
.
Ответ: (1; -1; 4).
Метод обратной матрицы. Запишем систему в виде матричного
уравнения: AX = B, где
233
112
111
A
,
z
y
x
X
,
2
7
4
B
.
Так как
09|| A
, то существует обратная матрица A
-1
, тогда
решение X = A
-1
B.
Найдем алгебраические дополнения элементов матрицы.
.
11
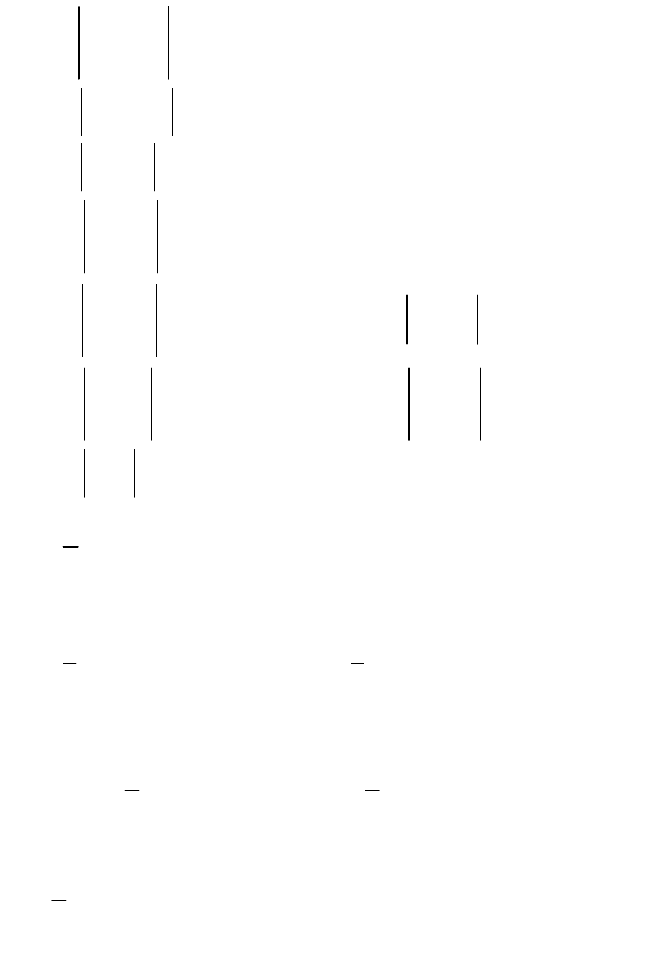
;532
23
11
11
A
;1)32(
23
11
21
A
;7)34(
23
12
12
A
;532
23
11
22
A
;336
33
12
13
A
;6)33(
33
11
23
A
;211
11
11
31
A
;321
12
11
33
A
;1)21(
12
11
32
A
363
157
215
9
1
1
A
.
Проверим выполнение равенства A
-1
A = E.
A
-1
A =
5 1 2 1 1 1 9 0 0 1 0 0
1 1
7 5 1 2 1 1 0 9 0 0 1 0
9 9
3 6 3 3 3 2 0 0 9 0 0 1
=E;
X=A
-1
B =
5 1 2 4 5 4 ( 1) 7 2 ( 2)
1 1
7 5 1 7 7 4 ( 5) 7 1 ( 2)
9 9
3 6 3 2 ( 3) 4 6 7 ( 3) ( 2)
=
9 1
1
9 1
9
36 4
.
Ответ: ( 1; -1; 4).
12
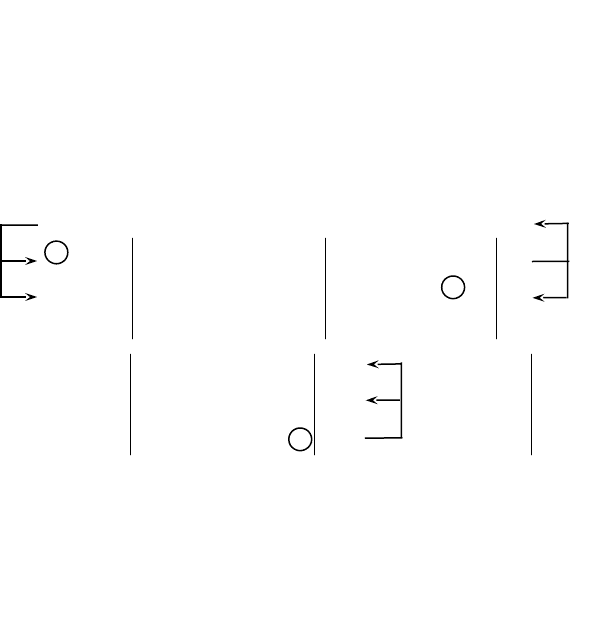
Решение № 41-60 аналогично решению приведенного примера.
Метод Жордана–Гаусса
Метод Жордана-Гаусса (метод последовательного исключения
неизвестных) применим для решения систем линейных алгебраических
уравнений при любом количестве решений. Он основан на элементарных
преобразованиях матриц:
- перестановках строк;
- умножении строки на число, отличное от нуля;
- прибавлении к элементам строки соответствующих элементов другой
строки, предварительно умноженных на некоторое число.
-
Рассмотрим случай единственного решения.
Пример:
Решить систему уравнений.
.1123
,17332
,1742
zyx
zyx
zyx
Решение.
Составим расширенную матрицу системы из коэффициентов при
неизвестных и свободных членов; последние отделим вертикальной чертой.
Приведем эту матрицу к диагональному виду, применяя метод элементарных
преобразований матриц. В итоге слева от черты получим единичную
матрицу.
( 2)
( 2)
( 3) ( 1)
1 2 4 17 1 2 4 17 1 2 4 17
2 3 3 17 ~ 0 1 5 17 ~ 0 1 5 17 ~
3 1 2 11 0 5 10 40 0 1 2 8
6
( 5)
1 0 6 17 1 0 6 17 1 0 0 1
~ 0 1 5 17 ~ 0 1 5 17 ~ 0 1 0 2
0 0 3 9 0 0 1 3 0 0 1 3
.
Ответ: (1; 2; 3).
Рассмотрим случай бесконечного множества решений.
Пример: Решить систему уравнений.
.3753
,2332
,142
zyx
zyx
zyx
13
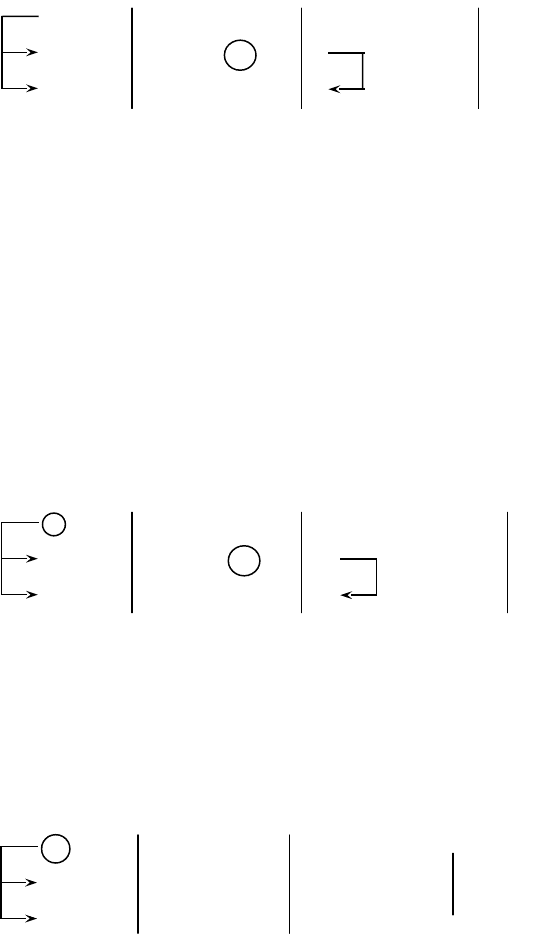
Решение:
( 2)
( 3) ( 1)
1 2 4 1 1 2 4 1 1 2 4 1
2 3 3 2 ~ 0 1 5 0 ~ 0 1 5 0
3 5 7 3 0 1 5 0 0 0 0 0
;
Так как одна строка состоит их нулей, то система имеет множество
решений. Запишем, учитывая последнюю матрицу, систему уравнений.
2 1 4 ; 1 6 ;
2 4 1;
5 ; 5 ; .
5 0.
. , .
x y t x t
x y z
y t y t
y z
z t z t t R
Ответ: (1+6t; -5t; t), где
Rt
.
Рассмотрим случай, когда система уравнений не имеет решений.
Пример: Решить систему уравнений.
.0753
,2332
,142
zyx
zyx
zyx
Решение.
( 2)
( 3) ( 1)
1 2 4 1 1 2 4 1 1 2 4 1
2 3 3 2 ~ 0 1 5 0 ~ 0 1 5 0
3 5 7 0 0 1 5 3 0 0 0 3
.
В последней строке пришли к противоречию 0x + 0y +0z = -3.
Ответ: система решений не имеет.
Пример: Решить систему уравнений.
.2936
,2624
,132
zyx
zyx
zyx
Решение.
( 2)
( 3)
2 1 3 1 2 1 3 1
2 1 3 1
4 2 6 2 ~ 0 0 0 0 ~
0 0 0 1
6 3 9 2 0 0 0 1
.
Ответ: система решений не имеет.
14

Решение номеров № 281-290 аналогично приведенным решениям.
Теорема Кронекера – Капелли
Ранг матрицы. Максимальный порядок r отличных от нуля миноров
матрицы А называется ее рангом, а любой минор порядка r, отличный от
нуля, называется базисным минором.
Элементарные преобразования матрицы не меняют ее ранга. Используя
эти преобразования, матрицу можно привести к такому виду, когда все ее
элементы, кроме a
11
, a
22
, …, a
rr
(r
min (m,n)) равны нулю. Очевидно, ранг
такой матрицы равен r.
Теорема. Для того, чтобы система алгебраических уравнений была
совместной, необходимо и достаточно, чтобы
.)|(, BAAгдеArangrangA
расширенная матрица системы
Пример:
Исследовать данные системы уравнений на совместность и решить их,
если они совместны.
2 2, 2 4 1, 2 3 1 7,
1) 2 3 1, 2) 2 5 1, 3) 4 2 1,
3 2 3. 2. 4 5.
x y z x y z x y z
x y z x y z x y z
x y z x y z x y
Решение.
Составим расширенную матрицу и методом элементарных
преобразований приведем ее к диагональному виду.
1)
( 2)
( 1)
2 1 1 2 1 2 3 1 1 2 3 1
1 2 3 1 ~ 2 1 1 2 ~ 0 5 5 0 ~
1 3 2 3 1 3 2 3 0 5 5 4
( 2)
5
1 2 3 1 1 0 1 1
~ 0 1 1 0 ~ 0 1 1 0
0 5 5 4 0 0 0 4
.
15
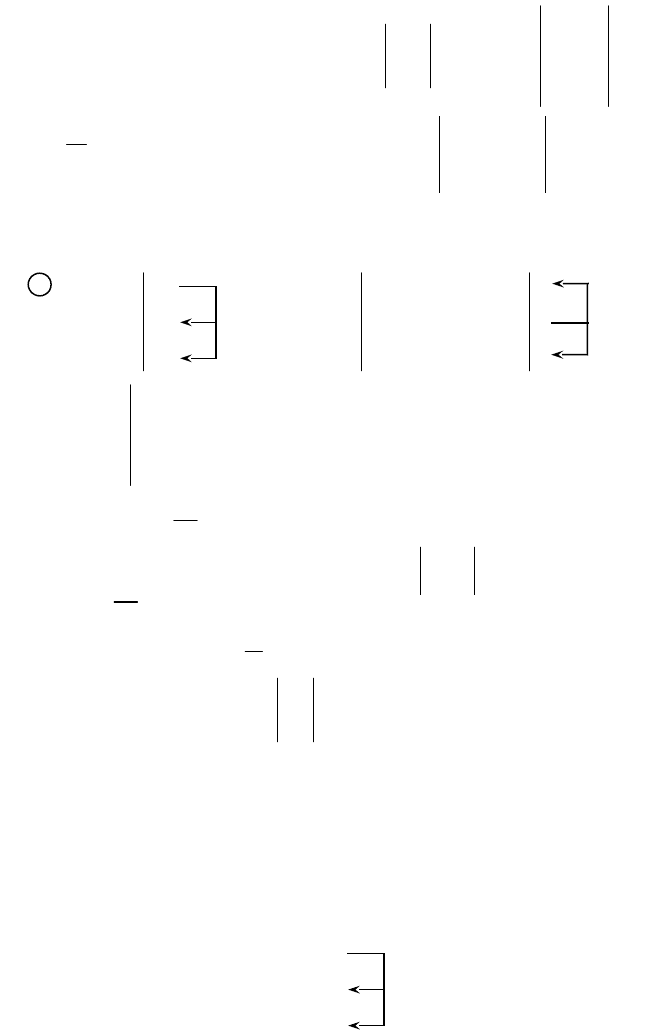
rang A = 2, так как минор второго порядка
1 0
1 0
0 1
, а:
1 0 1
0 1 1 0
0 0 0
, и
3Arang
, так как минор третьего порядка:
04
400
010
101
.
Так как
rangA rang A
, то по теореме Кронекера- Капелли система
несовместна, т.е. не имеет решений.
Ответ: система решений не имеет.
2)
( 2)
( 2)
( 1) ( 1)
1 2 4 1 1 2 4 1 1 2 4 1
2 1 5 1 ~ 0 3 3 3 ~ 0 1 1 1 ~
1 1 1 2 0 3 3 3 0 1 1 1
1 0 2 1
~ 0 1 1 1
0 0 0 0
.
Учитывая, что одна строка состоит из нулей, делаем заключение, что
rangA
и
Arang
не равны трём.
rangA
=2, так как минор второго порядка
01
10
01
.
Arang
=2, так как тот же минор, принадлежащий и расширенной
матрице, отличен от нуля.
Итак,
2 ArangrangA
. Исходная система совместна. Выберем в
качестве базисного минора M
2
=
1 0
0 1
. Тогда неизвестные x и y – базисные, z –
свободная переменная, а сокращенная система имеет вид:
.1
,12
zy
zx
Полагая z = c и решая сокращенную систему
относительно базисных неизвестных, получаем:
.1
,21
cy
cx
Следовательно, общее решение исходной системы имеет вид:
(-1+2c, 1+c, c).
16
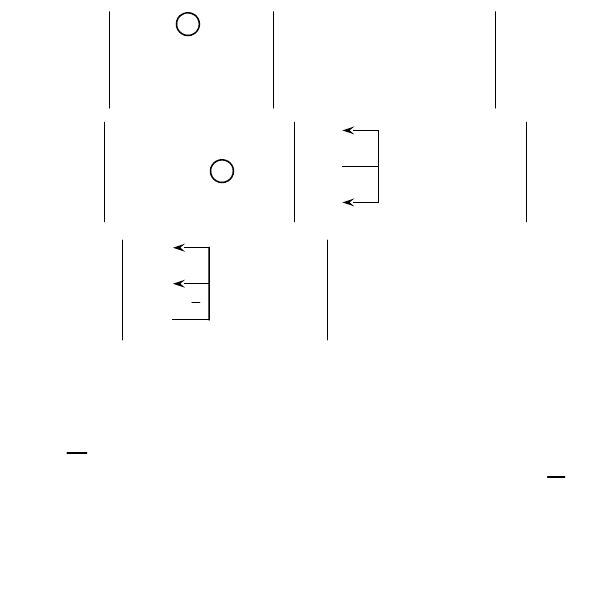
3)
( 2)
( 1)
2 3 1 7 1 4 2 1 1 4 2 1
1 4 2 1 ~ 2 3 1 7 ~ 0 11 3 5 ~
1 4 0 5 1 4 0 5 0 8 2 4
( 4)
( 11)
1 4 2 1 1 4 2 1 1 0 1 3
0 11 3 5 ~ 0 1 1/ 4 1/ 2 ~ 0 1 1/ 4 1/ 2 ~
0 4 1 2 0 11 3 5 0 0 1/ 4 1/ 2
.
2
1
1
100
010
001
~
2
2/1
3
100
4/110
101
)1(
)
4
1
(
3rangA
, так как минор третьего порядка
01
100
010
001
.
3Arang
, так как тот же минор не равен нулю и он же
принадлежит расширенной матрице. Так как
3 ArangrangA
и
равен количеству неизвестных системы, то система имеет единственное
решение.
Учитывая преобразованную матрицу, запишем систему в виде:
.2
,1
,1
z
y
x
Ответ: (-1; 1; -2).
Решение номеров 291-300 аналогично приведенным решениям.
17
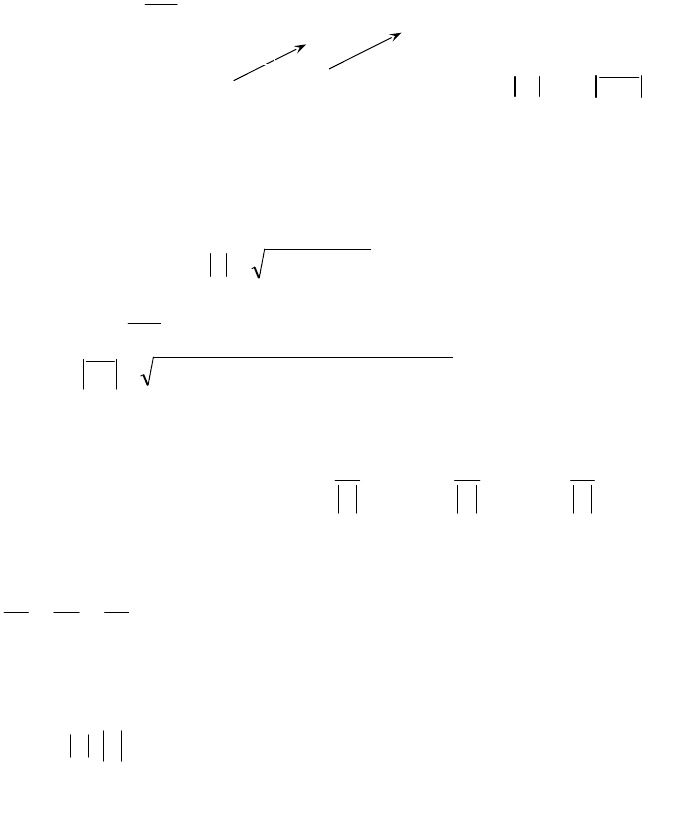
II. Векторная алгебра
Векторы в пространстве и на плоскости
Вектор
ABa
- это направленный отрезок.
Длина вектора называется модулем вектора; пишут
a
или
AB
.
Разложение вектора по координатным осям ОX, OY, OZ записывают в
виде
kajaiaa
zyx
, или
zyx
aaaa ,,
,где
zyx
aaa ,,
-
проекции вектора на оси ОX, OY, OZ;
kji
,,
- единичные векторы
(орты), совпадающие по направлению с этими осями. Проекции
zyx
aaa ,,
называются координатами вектора.
Длина вектора
222
:
zyx
aaaaa
. Если заданы начало вектора
111
,, zyxA
и конец
222
,, zyxB
, то координаты вектора находятся
по формуле
121212
;; zzyyxxAB
, а модуль вектора - по
формуле
2
12
2
12
2
12
zzyyxxAB
.
Если
,,
- углы между вектором
a
и осями ОX, OY, OZ, то
cos,cos,cos
называются направляющими косинусами вектора
a
и вычисляются по формулам:
cos ; cos ; cos
y
x z
a
a a
a a a
.
Два вектора
zyx
aaaa ;;
и
zyx
bbbb ;;
коллинеарны тогда и
только тогда, когда их соответствующие координаты пропорциональны:
z
z
y
y
x
x
b
a
b
a
b
a
.
Скалярным произведением двух векторов
a
и
b
называется число,
равное произведению длин этих векторов на косинус угла между ними:
.
,cos bababa
Если векторы заданы своими координатами, то
zzyyxx
babababa
.
a
А
В
18
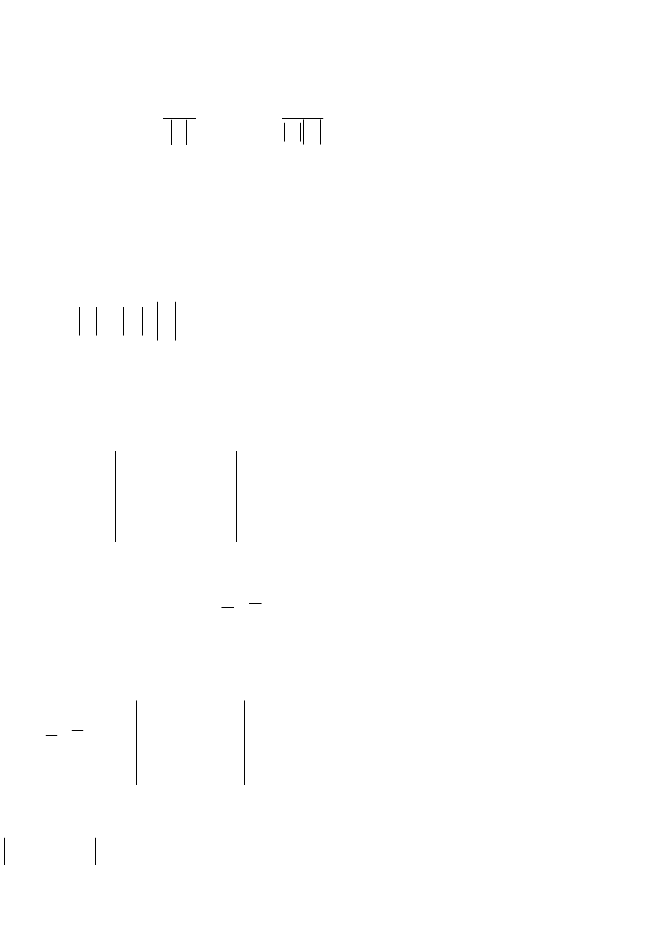
Два вектора
a
и
b
перпендикулярны тогда и только тогда, когда
0
zzyyxx
bababa
.
Проекция вектора
a
на вектор
b
и угол
вычисляются по
формулам:
b
ba
a
b
пр
;
.cos
ba
ba
Векторным произведением
a
b
двух векторов
a
и
b
называется
такой третий вектор
c
, длина которого численно равна площади
параллелограмма, построенного на двух данных векторах; этот вектор
перпендикулярен к плоскости параллелограмма и направлен так, что если
смотреть с его конца в основание, то кратчайший поворот от первого вектора
ко второму кажется совершающимся против хода часовой стрелки.
sinS c a b a b
.
Если векторы заданы своими координатами
, ,
x y z
a a a a
и
zyx
bbbb ,,
, то векторное произведение находится с помощью
определителя:
zyx
zyx
bbb
aaa
kji
ba
.
Смешанным произведением трех векторов
a
,
b
и
c
в указанном
порядке называется скалярное произведение векторного произведения
первых двух и третьего:
cba
.
Если векторы заданы своими координатами
zyx
aaaa ;;
,
zyx
bbbb ;;
,
zyx
cccc ;;
то смешанное произведение равно:
zyx
zyx
zyx
ccc
bbb
aaa
cba
;
Модуль смешанного произведения трех векторов равен объему
параллепипеда, построенного на этих векторах как на сторонах, т.е.
Vcba
. Три вектора
a
,
b
,
c
компланарны, т.е. параллельны
одной и той же плоскости, тогда и только тогда, когда их смешенное
произведение равно нулю:
0 cba
.
Пример:
Даны координаты вершин пирамиды ABCD. А(3;2;1), В(-2;1;-2), C(-1;2;3)
и D(1;-2;3). Требуется:
19
1) записать векторы
ACAB,
и
AD
в системе орт и найти модули этих
векторов;
2) найти угол между векторами
AB
и
AC
;
3) найти проекцию вектора
AD
на вектор
AB
;
4) найти площадь грани АВС;
5) найти объем пирамиды АВСD.
Решение.
1) Координаты векторов
ACAB,
и
AD
находим по формуле:
.;;
121212121212
kzzjyyixxzzyyxxAB
.242
);2;4;2()13;22;31(
;24
);2;0;4()13;22;31(
;35
kjiAD
AD
kiAC
AC
kjiAB
Модули векторов находим по формуле:
.622441642)4()2(
;522041620)4(
;359125)3()1()5(
.)()()(
222
222
222
2
12
2
12
2
12
AD
AC
AB
zzyyxxAB
Ответ:
,35 kjiAB
;35AB
kiAC
24
,
;52AC
kjiAD
242
,
.62AD
2) Угол между векторами находим по формуле:
ba
ba
cos
ba
bababa
zzyyxx
.
Тогда:
;
5
7
75
7
752
14
5257
620
2035
2)3(0)1()4)(5(
)cos(
ACAB
ACAB
ACAB
;
5
7
arccos
ACAB
20
