Владыкина Н.Д., Ермаков А.И., Курчанова С.С., Хмеленко Г.И. Методич. указания по курсу высшей математики. Часть 1
Подождите немного. Документ загружается.


Рекомендации к выполнению заданий №№ 201-220.
Геометрический смысл производной: число
)('
0
xf
равно угловому
коэффициенту касательной к кривой у = f (x) в точке М
0
(x
0
; f (x
0
)), т. е.
tgxf )('
0
.
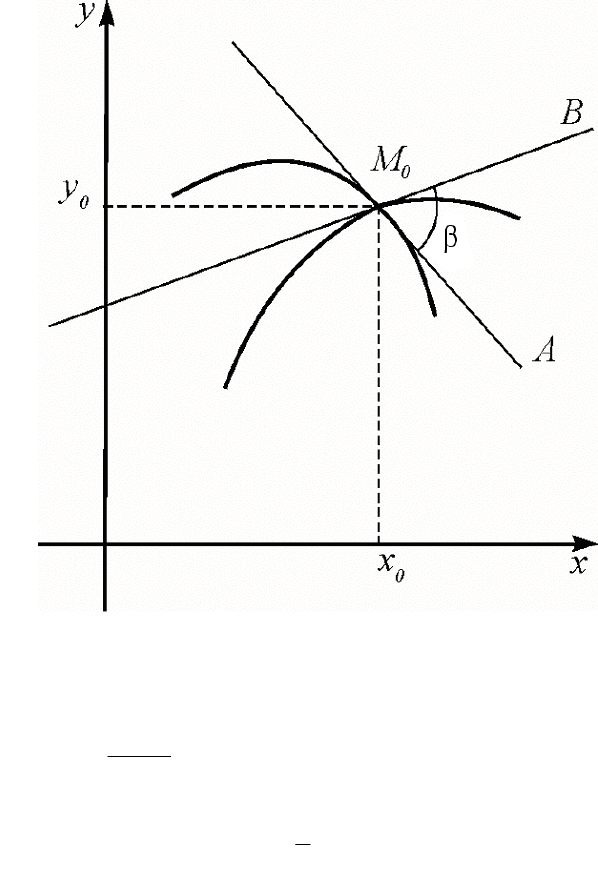
Под углом между кривыми y = f
1
(x) и y = f
2
(x) в их общей точке М
0
(x
0
; y
0
)
понимается угол β между касательной M
0
A и M
0
B к этим кривым в точке М
0
.
По известной формуле аналитической геометрии получаем:
tg β =
)(')('
)(')('
0102
0102
xfxfl
xfxf
71
Из геометрического смысла производной следует, что уравнение
касательной к кривой y = f (x) в точке M
0
(x
0
; y
0
) будет:
y – y
0
= y’(x
0
)(x-x
0
).
Прямая, проходящая через точку касания перпендикулярно к
касательной, называется нормалью. Для нормали получаем уравнение:
)(
)('
1
0
0
0
xx
xy
yy
или
0 0 0
'( ) ( ) 0x x y x y y
.
Пример:
Дано уравнение параболы
2
1
( 1)
2
y x
и точка C(0; 0), которая
является центром окружности R = 5. Требуется:
1) Найти точки пересечения параболы с окружностью;
2) Составить уравнение касательной и нормали к параболе в точках ее
пересечения с окружностью;
72

3) Найти острые углы, образуемые кривыми в точках их пересечения.
Сделать чертеж.
Решение:
1. Составим уравнение окружности с центром в точке C(0; 0) и радиусом
R = 5.
Каноническое уравнение окружности – (x – x
0
)
2
+ (y – y
0
)
2
= R
2
, где C(x
0
;
y
0
) - центр окружности, R – радиус. Т.к. C(0; 0) - центр окружности, то x
2
+
y
2
=25 - уравнение окружности с центром в начале координат и радиусом R =
5.
2. Находим точки пересечения параболы
2
1
( 1)
2
y x
и окружности x
2
+ y
2
=25, решив систему:
2
2 2
1
( 1), (1)
2
25. (2)
y x
x y
Из уравнения (1): x
2
= 2y + 1.
Подставим в уравнение (2)
2y + 1 + y
2
= 25 y
2
+ 2y – 24 y
1
= -6 и y
2
= 4
По теореме Виета, корни уравнения y
1
= – 6; y
2
= 4.
Найдем х используя, например, уравнение
2
2 1x y
2
1
2
2 1 2
6, 2( 6) 1 11
4, 2 4 1 9 3, 3
y x x
y x x x
Точки пересечения параболы
2
1
( 1)
2
y x
и окружности x
2
+ y
2
=25 –
точки A
1
(3; 4) и A
2
(-3; 4).
3. Чтобы составить уравнение нормали и касательной нужно знать
значение производной в точках касания
;2
2
1
))'1(
2
1
('
2
xxy
y’ = x
В точке A
1
(3; 4); y’(A
1
) = 3; y(A
1
) = 4
В точке A
2
(-3; 4) y’(A
2
) = -3; y(A
2
) = 4
Уравнение касательной:
)()('
000
xxxyyy
Уравнение нормали:
)(
)('
1
0
0
0
xx
xy
yy
В точке A
1
(3; 4) касательная имеет уравнение y – 4 = 3(x - 3) или y = 3x –
5, 3x – y – 5 = 0 уравнение нормали в точке A
1
(3; 4) имеет вид:
73
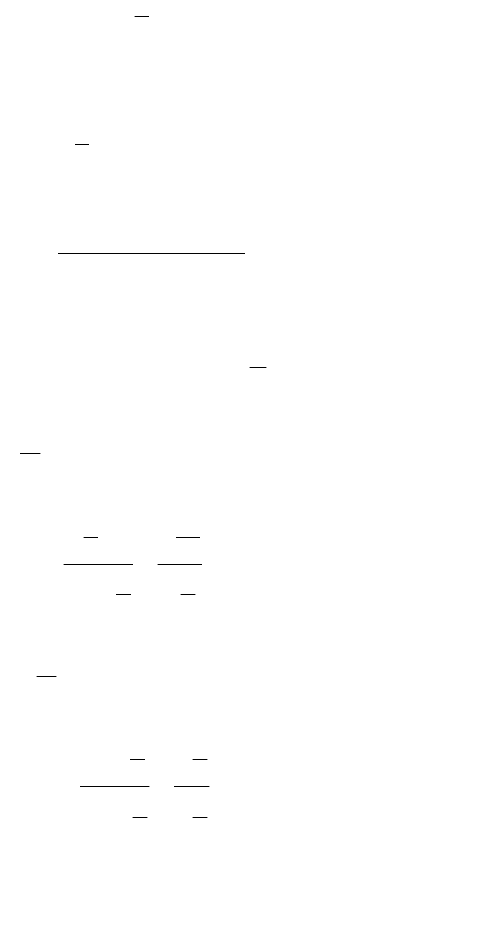
)3(
3
1
4 xy
или
3 15 0x y
.
В точке A
2
(-3; 4) касательная имеет уравнение:
y – 4 = – 3(x + 3) и 3x + y + 5 = 0.
Уравнение нормали в этой точке имеет вид:
1
4 ( 3)
3
y x
3 12 3 3 15 0y x x y
.
4. Найдем углы, образуемые кривыми в точках их пересечения, как углы
между касательными, воспользовавшись формулой:
tg β =
)()('1
)()('
0201
0102
xyxy
xyxy
.
Найдем угловые коэффициенты касательных к окружности и параболе.
Уравнение окружности x
2
+ y
2
=25. Продифференцируем это равенство:
2x
+ 2yy’ = 0. Отсюда
' .
x
y
y
Для параболы y’ = x.
В точке A
1
(3; 4) угловой коэффициент касательной к окружности y
2
’(A
1
) =
–
4
3
; угловой коэффициент касательной к параболе y
1
’(A
1
) =3.
Тогда угол между касательными в точке A
1
определим из формулы:
tg β
1
=
3 15
3
4 4
3;
3 5
1 3
4 4
tg β
1
= 3; β
1
= arctg 3
72
.
В точке A
2
(-3; 4) угловой коэффициент касательной к окружности y
2
’(A
1
)
= –
4
3
; угловой коэффициент касательной к параболе y
2
’(A
1
) = – 3;.
Тогда угол между касательными в точке A
2
равен
tg β
2
=
3 5
3
4 4
3;
3 5
1 3
4 4
tg β
2
=3;
β
2
= arctg β
2
arctg 3
72
.
Острые углы, образуемые кривыми в точках их пересечения
β
1
72
, β
2
72
.
74

Полное исследование функции и построение графика
Пример. Исследовать функцию
2
)1(
2
x
x
y
и построить ее график.
Решение:
1. Область существования функции: x – 2
0
x
2
. Значит D(y):
(x
; 2)
;2(
).
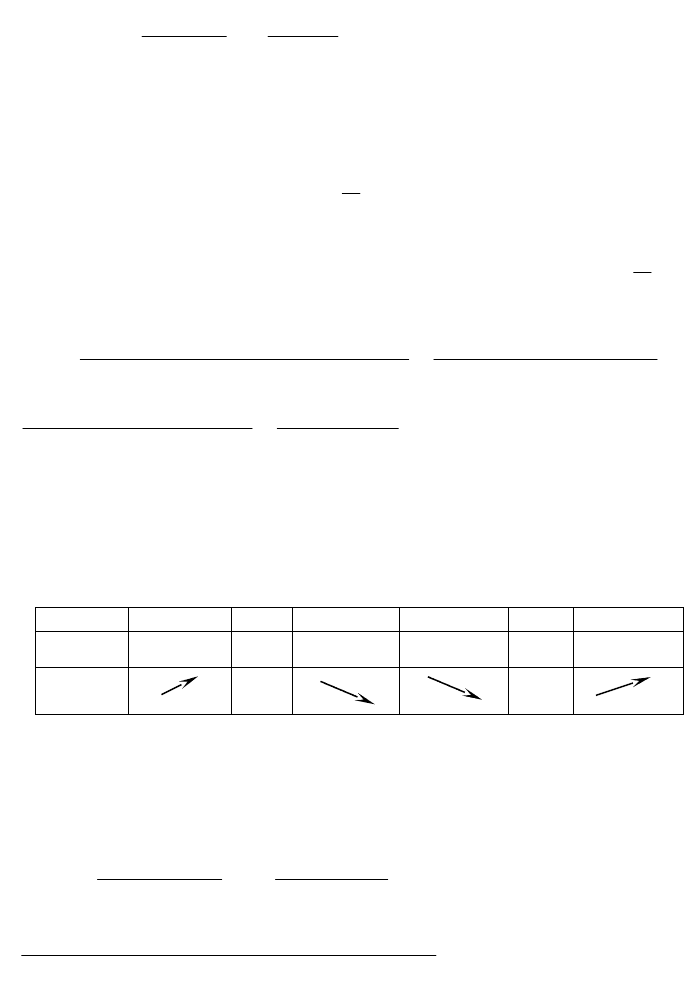
2. Точка x = 2 – точка разрыва второго рода, т.к.
2 2
2 0 2 0
( 1) ( 1)
lim , lim
2 2
x x
x x
x x
75
3.
2 2
( 1) ( 1)
( ) ;
2 2
x x
f x
x x
функции общего вида: ни четная, ни
нечетная. Для четной функции y(- x ) = y( x ); для нечетной функции y(- x ) = -
y( x ). Эти условия не выполнены.
4. Функция непериодическая:
xf (
Т)
)(xf
ни при каких Т.
5. Ищем точки пересечения графика функции с осями координат;
при x = 0, y =
2
1
.
при y = 0, (x+1)
2
= 0, x = – 1.
Следовательно, точки пересечения с осями координат: (-1; 0) и (0;
2
1
).
6. Найдем первую производную:
2 2 2
2 2
2 2
(( 1) ) ' ( 2) ( 2) ' ( 1) 2( 1)( 2) ( 1)
'( )
( 2) ( 2)
( 1)(2( 2) ( 1)) ( 1)( 5)
.
( 2) ( 2)
x x x x x x x
f x
x x
x x x x x
x x
7. Для нахождения критических точек решим уравнение f’(x) = 0, т.е (х+1)
(x – 5) = 0, откуда x
1
= - 1; x
2
= 5 (x = 2 - точка, в которой производная не
существует, но это значение не рассматривается, так как х = 2 не
принадлежит области определения функции). Точки x
1
= - 1, x
2
= 5, x
3
= 2
делят область определения функции на интервалы (- ; - 1); (- 1; 2); (2; 5); (5; +
), на которых производная сохраняет знаки «+» или «–».
x (- ∞; - 1) - 1 (- 1; 2) (2; 5) 5 (5; + ∞)
y' + 0 - - 0 +
y
0
max
12
min
Функция возрастает при
x
(- ; - 1)
(5; + )
Функция убывает при
x
(- 1; 2)
(2; 5).
При х = – 1 функция имеет максимум, y
max
= y (- 1) = 0
При х = 5 функция имеет минимум, y
min
= y(5) = 12.
8. Вторая производная
'
'
2
2 2
( 1)( 5) 4 5)
''( )
( 2) ( 2)
x x x x
f x
x x
2 2 2 2
4
4 5)'( 2) ( 4 5)(( 2) '
( 2)
x x x x x x
x
76

2 2 2
4 4
(2 4)( 2) ( 4 5) 2( 2) ( 2)((2 4)( 2) 2( 4 5)
( 2) ( 2)
x x x x x x x x x x
x x
2 2
3 3
2 8 8 2 8 10 18
( 2) ( 2)
x x x x
x x
Вторая производная не обращается в нуль, следовательно, критических
точек нет, точек перегиба нет. Замечаем, что f’’(x) < 0 на интервале (- ; 2)
(здесь функция выпукла) и f’’(x) > 0 на интервале (2; + ) (здесь функция
вогнута).
9. Определяем асимптоты. Вертикальная асимптота одна, ее уравнение х
= 2. Выясним наличие наклонных асимптот y = =kx+ b
2 2
2
( ) ( 1)
lim lim lim 1;
( 2)
x x x
f x x x
k
x x x x
2 1 4 1
lim( ( ) ) lim lim 4
2 2
x x x
x x x
b f x kx x
x x
Следовательно, y = x + 4 - наклонная асимптота. Строим график.
Наибольшее и наименьшее значения функции (№№241-260)
77
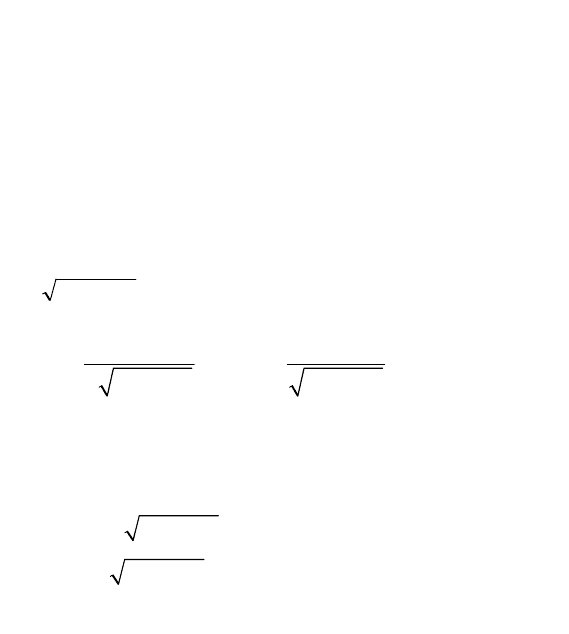
Своего наибольшего и наименьшего значения функция может достигать
либо в точках экстремума, либо на концах отрезка. Поэтому, для того, чтобы
найти наибольшее и наименьшее значения функции
xfy
на отрезке
,a b
, нужно:
1. найти критические точки функции, т.е. те точки, в которых
0' xf
, и
'f x
не существует
2. выбрать из них те, которые принадлежат отрезку
,a b
.
3. найти значение функции в выбранных точках и на концах интервала,
т.е.
af
и
bf
.
4. из полученных значений выбрать наименьшее и наибольшее.
Пример: найти наибольшее и наименьшее значение функции
2
100 xy
на отрезке
6; 8
.
Решение:
2 2
1
' 2 .
2 100 100
x
y x
x x
0'y
при
0x
6; 8
.
'y
-не существует при
10 [ 6; 8].x
0 10,
6 100 36 8,
8 100 64 6.
y
y
y
Отсюда видно:
. .
0 10; 8 6
наиб наим
y y y y
.
Решение текстовых задач на наибольшее и
наименьшее значение.
Пример 1.
Требуется изготовить коническую воронку с образующей, равной 20см.
Какова должна быть высота воронки, чтобы ее объем был наибольшим.
Решение.
78

1. Составим функцию, которая задает объем воронки.
2. В качестве аргумента
x
нужно взять высоту воронки.
2
1
3
конуса
V R H
, где
R
- радиус основания,
H
- высота конуса.
В нашем случае
xH
, тогда
222
20 xR
xxxV
22
20
3
1
. При этом
0; 20x
.
Дальше решаем задачу на нахождение наибольшего значения функции
xV
на отрезке
20;0
.
3
3 2
1
400 ;
3
1 1
' 400 ' (400 3 );
3 3
V x x x
V x x x x
0' xV
, если
2 2
400 20
400 3 0 3 400 ;
3
3
x x x
Учитывая условия задачи
20
;
3
x
2
0 20 0;
20 1 400 20 400 1 20 400 40 16000
400 1 .
3 3 3 3
3 3 3 3 3 9 3
V V
V
Ответ: высота =
3
20
см.
Пример 2.
Через данную точку
1; 4P
провести прямую так, чтобы сумма длин
положительных отрезков, отсекаемых ею на координатных осях, была
наименьшей.
Решение:
20
x
79

1)Функция должна задавать сумму длин отрезков
OA
и
OB
.
2)Провести прямую – значит записать ее уравнение.
Запишем уравнение прямой линии в отрезках:
1
x y
a b
, где
OAa
,
OBb
при этом сумма.
baS
должна быть наименьшей
S
является
функцией двух переменных
a
и
b
. Используем тот факт, что точка
1; 4P
лежит на прямой. Это означает, что ее координаты удовлетворяют
уравнению прямой:
1
41
ba
.
Выразим отсюда
b
:
ab
1
1
4
;
1
414
a
a
b
a
a
b
,
тогда
1
4
a
a
aS
,
1
4
a
a
aaS
,
(1; ).a
2
2 2 2
4 1 4 1 4
4
' 1 1 ;
1 1 1
a a a
S a
a a a
0' aS
, если
2
1
1 4 1 2 3;a a a
2
1 (1; );a
80
