Власов К.П., Анашкин А.С. Теория автоматического управления
Подождите немного. Документ загружается.


Размерность
управляемой части системы совпадает с
рангом матрицы:
knn
n
BABAABBU
12
...
.
При
n
система полностью управляема, при
n0
– не
полностью управляема, при
0
– неуправляема.
Размерность
наблюдаемой части системы совпадает с
рангом матрицы:
mnn
n
CACACACV
12
)(...)(
.
При
n
система полностью наблюдаема, при
n0
– не
полностью наблюдаема; при
0
– ненаблюдаема.
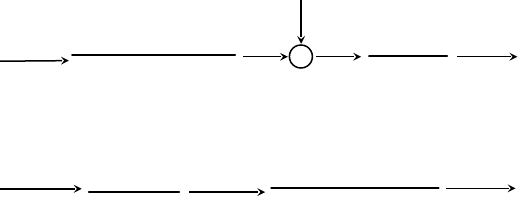
➢;;;Приме р11. Рассмотрим систему, изображенную на
рис.5.31,;а. Количество фазовых координат
3n
(они обусловлены
наличием в;системе емкостей
321
,, TTT
). В отсутствие
управляющего сигнала
2
u
управление
1
u
воздействует только на
две фазовые координаты, обусловленные емкостями
2
T
и
3
T
(
1
T
сокращается), т.е.
32 n
, и система не полностью управляема.
При подаче сигнала
2
u
появляется воздействие и на фазовую
координату
1
T
, система становится полностью управляемой (
3 n
).
Система, изображенная на рис.5.31,;б, не полностью
наблюдаема, так как в формировании выхода
y
участвуют только
две фазовые координаты из трех (
2
T
и
3
T
). При подаче
управляющего сигнала между двумя звеньями системы фазовая
координата
1
T
становится наблюдаемой, поскольку также
участвует в формировании выхода системы.
Таким образом, понятие управляемости системы
характеризует способность входа
)(tu
возбуждать все переменные
состояния (фазовые координаты) выхода
)(t
; понятие
наблюдаемости – способность состояния
)(t
создавать выходной
сигнал
)(ty
.
61
6. УСТОЙЧИВОСТЬ АСУ
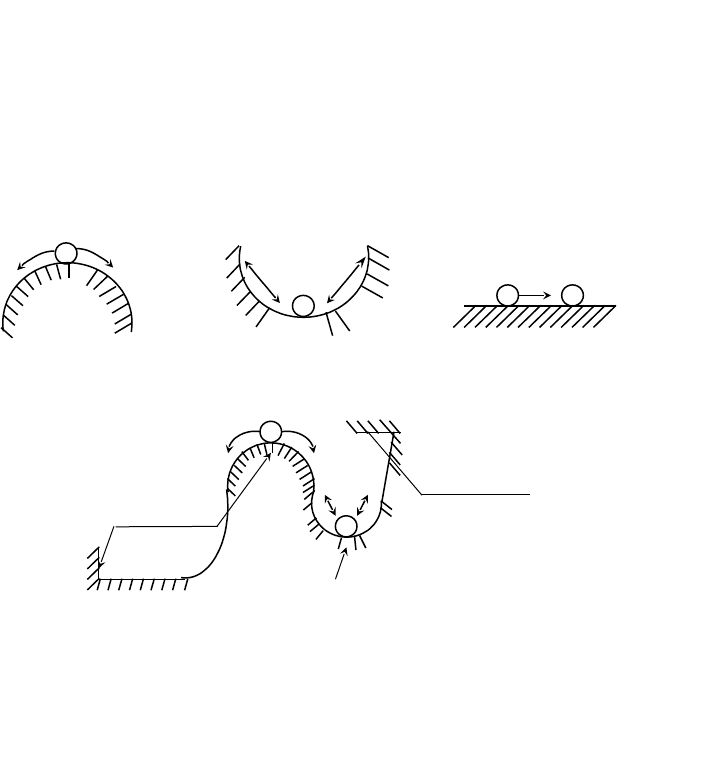
Устойчивость АСУ характеризует способность системы
возвращаться в состояние равновесия после исчезновения внешних
сил, которые вывели ее из этого состояния (рис.6.1).
Система устойчива в малом, если констатируют лишь факт
наличия области устойчивости, но не определяют каким-либо
образом ее границы. Система устойчива в большом, если
определены границы устойчивости, т.е. границы области начальных
отклонений, при которых система возвращается в состояние
равновесия, и выяснено, что реальные начальные отклонения
принадлежат этой области.
62
)1)(1(
1
32
1
pTpT
pT
1
1
1
pT
2
u
y
1
1
1
pT
)1)(1(
1
32
1
pTpT
pT
y
а
u
1
u
б
Рис.5.31
Когда система возвращается в состояние равновесия при
любых начальных отклонениях, ее называют устойчивой в целом,
т.е. в;малом и большом.
6.1. Переходные процессы в АСУ
В любой АСУ в результате воздействия возмущающих сил,
с;одной стороны, и восстанавливающего действия управляющего
устройства, с другой, возникает переходный процесс: переход АСУ
из одного состояния в другое. Рассмотрим различные типы
переходного процесса.
Пусть АСУ описывается дифференциальным уравнением вида
kxyyTyT
2
2
. (6.1)
63
Ограничения
Ограничение
Безразличное
равновесие
Неустойчивое
равновесие
Устойчивое
равновесие
Устойчивость в малом
Рис.6.1
Характеристическое уравнение ДУ (6.1)
012
22
pTpT
с корнями
Tp /1
2
2,1
.
Решение ДУ (6.1) представляет собой кривую переходного
процесса y(t), характер которого определяется коэффициентом .
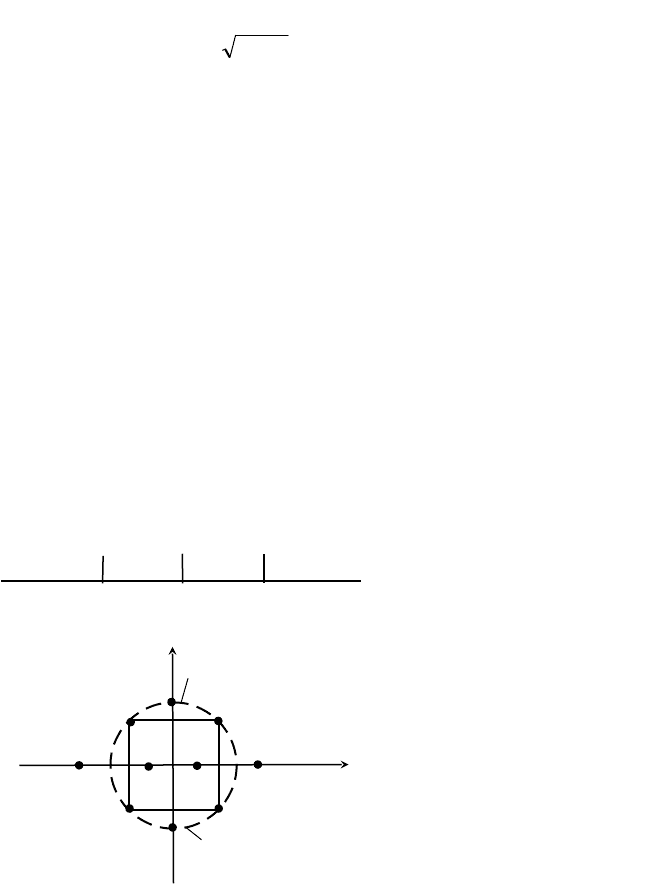
Расположение корней характеристического уравнения на
комплексной плоскости p при различных значениях показано на
рис.6.2. Рассмотрим переходные процессы, соответствующие
различным значениям .
I.;;<;–1. Переходная функция h(t) при подаче на вход
единичного ступенчатого сигнала
tp
cth
1
e)(
1
kc
tp
2
e
2
, при
этом корни вещественные положительные
0
I
2,1
p
, следовательно,
)(lim th
t
.
В данном случае система не может восстановить
равновесное состояние, значение управляемой координаты все
больше отклоняется от заданного. Такой переходный процесс
называется расходящимся монотонным (апериодическим)
64
I
II III
IV
1
–1
0
< –1
–
> 1
–1 < <0
0< <1
( = 1)
( = 0)
+j/T
+j
( = 0)
( = –1)
–j
III II
–j/T
1/T
–1/T
I
IV
Рис.6.2
p
1
II
p
1
III
p
2
II
p
2
I
p
1
I
p
2
III
p
1
IV
p
1
V
p
2
IV
p
2
V
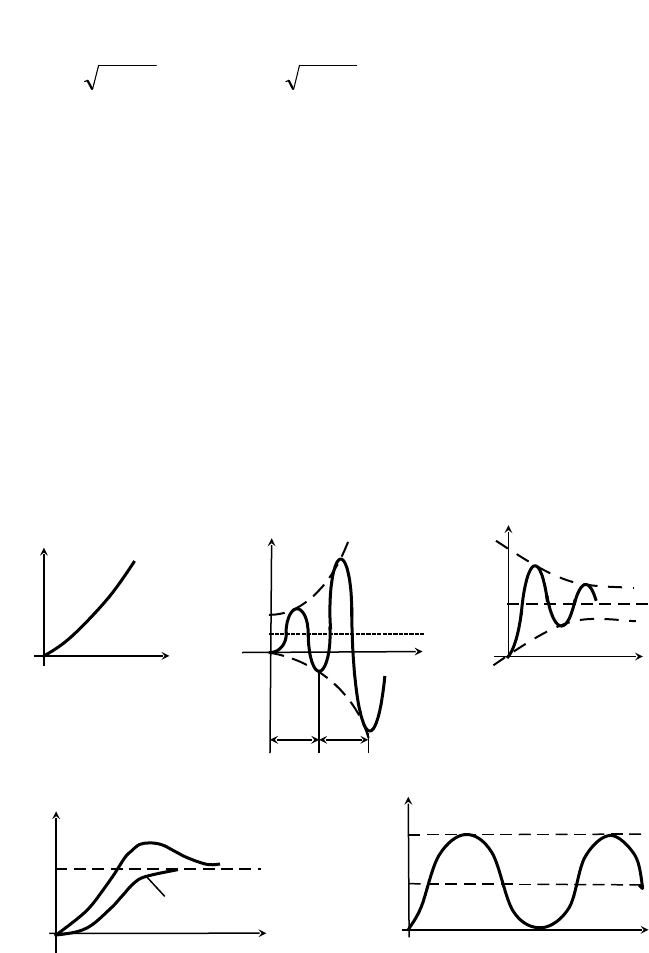
(рис.6.3,;а), а система неустойчивой (идет процесс накопления
энергии из внешней среды).
II.;–1;<;;<;0. При этом
II
1,2
p
=4;;j, ;>;0, а
переходная;;функция h(t)4=4k[14+4Ae
t
sin(t4+4)], где
,1/1
2
A
.1arcsin
2
Характеристики системы те
же, что и в предыдущем случае, но переходный процесс
колебательный (рис.6.3, б).
III.;0;<;;<;1. Передаточная функция h(t) та же, что и в
случае;II, но при ;<;0.
Система возвращается к равновесному состоянию. Значение
управляемой координаты приближается к заданному. Такой
переходный процесс называется сходящимся колебательным, а
система устойчивой (происходит диссипация энергии во внешнюю
среду) (рис.6.3, в).
65
t
h(t)
а
k
t
h(t)
в
= 1
> 1
k
h(t)
t
г
h(t)
t
2k
k
д
Рис.6.3
2k
k
e
t
t
h(t)
T T
б

IV.;;>;1. Переходная функция h(t) имеет тот же вид, что и в
случае I, но p
1,2
;<;0. Характеристика системы та же, что и в III случае,
но переходный процесс монотонный (апериодический) (рис.6.3, г).
V.;4=40;
V
1,2
p
=4j, 4=40, h(t)4=4k(1;–;cost).
В системе устанавливается периодическое движение,
процесс называется колебательным незатухающим, система
находится на границе устойчивости (рис.6.3, д). Она является
замкнутой (консервативной), автономной от внешней среды.
Все рассмотренные колебания (II, III и V случаев) относятся
к классу свободных, их параметры A и зависят от начальных
условий, т.е. от привнесенной энергии.
Для случаев II и III функция h(t);;h(t4+4T), где T– период,
следовательно, это колебания непериодические.
Периодические колебания наблюдаются только в случае;V.
Они являются собственными, а для линейной системы и свободными.
Если колебания вызваны периодическими внешними
воздействиями (x(t)4=4asint), их называют вынужденными.
Заметим, что периодические движения могут возникать и в
нелинейной системе, причем они не обусловлены внешними
воздействиями и не зависят от начальных условий. Эти колебания
относятся к собственным и несвободным и называются
автоколебаниями.
Сопоставление корней характеристического уравнения на
комплексной плоскости p с соответствующими переходными
процессами (рис.6.3) показывает, что линейная система
восстанавливает равновесное состояние, если корни
характеристического уравнения расположены слева от мнимой оси.
В общем случае условие устойчивости АСУ имеет вид
)0()(lim yty
t
,
где y(0) – начальное значение управляемой величины;
)0()( yy
– установившееся отклонение управляемой
величины или статическая ошибка, в случае астатической системы
4=40.
66
Реальные системы всегда нелинейны, однако если для анализа
поведения системы можно произвести линеаризацию уравнений, то о
ее устойчивости можно судить исходя из первой теоремы Ляпунова:
1.;Если характеристическое уравнение линеаризованной
системы имеет все корни с отрицательными вещественными
частями, то реальная система будет устойчива в малом.
2.;Если характеристическое уравнение линеаризованной
системы имеет хотя бы один корень с положительной вещественной
частью, то реальная система всегда неустойчива.
3.;Если характеристическое уравнение линеаризованной
системы имеет хотя бы один нулевой корень или пару чисто
мнимых корней, то поведение реальной системы не может
определяться ее;линеаризованным уравнением. В этом случае
отброшенные при линеаризации уравнения члены высшего порядка
малости определяют поведение системы и могут превратить ее как в
устойчивую, так и в;неустойчивую.
Анализ устойчивости линеаризованной системы сводится
к;нахождению расположения корней на комплексной плоскости,
которое однозначно определяется коэффициентами
характеристического уравнения. Однако не всегда можно вычислить
корни характеристического уравнения в аналитическом виде. В
соответствии с;теоремой Абеля, корни уравнения выше четвертого
порядка не могут быть найдены аналитически в принципе. Поэтому
желательно иметь такие критерии, с помощью которых можно было
судить об устойчивости системы непосредственно по
коэффициентам характеристического уравнения. Эти критерии
называют критериями устойчивости и подразделяют на
алгебраические (например, критерий Гурвица) и частотные
(критерии Михайлова и Найквиста).
6.2. Алгебраический критерий устойчивости
Гурвица
Пусть дано характеристическое уравнение системы вида
a
0
p
n
4+4a
1
p
n-1
4+4a
2
p
n-2
4+4…4+4a
n-1
p4+4a
n
4=40 при a
0
;>;0. (6.2)
67

Гурвиц предложил алгебраический критерий, который
основан на построении специальных определителей
характеристического уравнения (6.2), называемых определителями
Гурвица. Они составляются по следующим правилам:
1);по главной диагонали выписывают все коэффициенты от
a
1
до a
n
в порядке возрастания индекса;
2);дополняют столбцы определителя вверх от диагонали
с;коэффициентами последовательно возрастающими, а вниз – с
последовательно убывающими индексами;
3);на место коэффициентов, индексы которых больше n
и;меньше 0, ставят нули.
В соответствии с этими правилами, определитель Гурвица
n-го порядка для уравнения (6.2) имеет вид
n
n
a
aa
aaa
aaa
000
00
0
0
31
420
531
. (6.3)
Определители Гурвица более низкого порядка являются
диагональными минорами
n
, например, при n4=43
1
4=4a
1
;
20
31
2
aa
aa
;
31
20
31
3
0
0
0
aa
aa
aa
.
Поскольку в последнем столбце определителя
n
стоят нули,
за исключением a
n,
то
n
4=4a
n
n –1
. (6.4)
Критерий Гурвица формулируется следующим образом: для
устойчивости АСУ необходимо и достаточно, чтобы все
определители Гурвица
1
,
2
, …,
n
были положительными и при
этом выполнялось условие a
0
;>;0.
➢ П ример 12. 1.;Пусть АСУ описывается уравнением второго
порядка, тогда характеристическое уравнение имеет вид
a
0
p
2
4+4a
1
p4+4a
2
4=40,
68

а определитель Гурвица
20
1
2
0
aa
a
.
Условие устойчивости
a
0
;>;0;
1
4=4a
1
;>;0;
2
4=4a
2
1
4=4a
2
a
1
;>;0.
Поскольку a
1
;>;0, должно выполняться условие a
2
;>;0.
Таким образом, для устойчивости системы второго порядка
необходимо и достаточно, чтобы все коэффициенты
характеристического уравнения были положительными.
2.;Пусть АСУ описывается ДУ третьего порядка,
характеристическое уравнение которого имеет вид
a
0
p
3
4+4a
1
p
2
4+4a
2
p4+4a
3
4=40,
а определитель Гурвица
23
31
20
31
3
0
0
0
a
aa
aa
aa
.
Для устойчивой системы имеем
3
4=4a
3
2
;>;0;
0
3021
20
31
2
aaaa
aa
aa
;
1
4=4a
1
;>;0; a
0
;>;0.
Следовательно, a
3
;>;0 и a
2
;>;0, т.е. условие положительности
всех коэффициентов выдерживается. Кроме того, необходимо,
чтобы a
1
a
2
;>;a
0
a
3
.
*;*;*
Таким образом, для уравнений выше второго порядка
положительность всех коэффициентов является необходимым
условием устойчивости АСУ. Но это условие не является
достаточным, так как
2
может не быть положительным при
положительных a
0
, a
1
, a
2
, a
3
. Условие
2
;>;0 позволяет в случае
неустойчивой системы изменить ее параметры таким образом,
чтобы она стала устойчивой.
69
Для характеристических уравнений высоких степеней (n;>;5)
анализ влияния коэффициентов на определитель Гурвица резко
усложняется. Свободными от этого недостатка являются частотные
критерии устойчивости.
6.3. Частотные критерии устойчивости
Эти критерии основаны на анализе расположения тех или
иных частотных характеристик на плоскости. При этом достигается:
1);наглядность, так как задача исследования системы любого
порядка сводится к изучению плоской кривой;
2);возможность экспериментального определения частотных
характеристик системы, что позволяет исследовать такие системы,
ДУ которых неизвестны;
3);сравнительно простой анализ влияния того или иного
параметра на устойчивость, а также возможность суждения о
качестве переходного процесса.
Частотные критерии можно разделить на две группы: первые
предназначены для исследования замкнутой системы – критерий
Михайлова (он применяется обычно для сложных систем); вторые –
для исследования устойчивости замкнутой системы по частотной
характеристике разомкнутой системы – критерий Найквиста
(используется, когда размыкание системы приводит к существенным
упрощениям частотной функции).
Критерий устойчивости Михайлова. Пусть дано
уравнение замкнутой системы Y(p)4=4W(p)X(p), где W(p)4=4В(p)/
А(p) – передаточная функция замкнутой системы. Тогда ДУ
системы, преобразованное по Лапласу,
A(p)Y(p)4=4B(p)X(p).
Характеристический полином этого уравнения имеет вид
A(p)4=4a
0
p
n
4+4a
1
p
n;–;1
4+4…4+4a
n;–;1
p4+4a
n
.
В соответствии с основной теоремой алгебры этот полином
можно разложить на множители:
A(p)4=4a
0
(p;–;p
1
)(p;–;p
2
);…;(p;–;p
n
), (6.5)
где p
1
, …, p
n
– корни характеристического уравнения A(p)4=40.
70
