Ревинская О.Г., Кравченко Н.С. Изучение моделей физических процессов и явлений на компьютере
Подождите немного. Документ загружается.


ɆɨɞɄ-05 ɋɥɨɠɟɧɢɟ ɤɨɥɟɛɚɧɢɣ. Ȼɢɟɧɢɹ
281
ɡɭɥɶɬɢɪɭɸɳɢɟ ɤɨɥɟɛɚɧɢɹ (ɛɢɟɧɢɹ) ɫɨɜɟɪɲɚɸɬɫɹ ɫ ɱɚɫɬɨɬɨɣ
:
, ɩɪɢ ɷɬɨɦ
ɚɦɩɥɢɬɭɞɚ ɤɨɥɟɛɚɧɢɣ ɦɟɞɥɟɧɧɨ ɦɟɧɹɟɬɫɹ ɫɨ ɜɪɟɦɟɧɟɦ ɨɬ ɪɚɡɧɨɫɬɢ ɞɨ
ɫɭɦɦɵ ɚɦɩɥɢɬɭɞ ɫɤɥɚɞɵɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ ɩɨ ɩɟɪɢɨɞɢɱɟɫɤɨɦɭ ɡɚɤɨɧɭ.
ɑɚɫɬɨɬɚ ɢɡɦɟɧɟɧɢɹ ɚɦɩɥɢɬɭɞɵ ɛɢɟɧɢɣ ɪɚɜɧɚ ɪɚɡɧɨɫɬɢ ɱɚɫɬɨɬ ɫɤɥɚɞɵ-
ɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ
Z'
ɢ ɧɚɡɵɜɚɟɬɫɹ ɱɚɫɬɨɬɨɣ ɛɢɟɧɢɣ. Ɍɨɝɞɚ ɜɟɥɢɱɢɧɚ
:
S
:
2
T
ɧɚɡɵɜɚɟɬɫɹ ɩɟɪɢɨɞɨɦ ɤɨɥɟɛɚɧɢɣ, ɚ ɜɟɥɢɱɢɧɚ
Z'
S
'
2
T
– ɩɟɪɢɨ-
ɞɨɦ ɛɢɟɧɢɣ (ɪɢɫ. 2).
Ʉɪɢɬɟɪɢɣ ɧɚɛɥɸɞɟɧɢɹ ɛɢɟɧɢɣ ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ ɜ ɜɢɞɟ
1
Z
Z'
ɢɥɢ
':
TT . Ⱦɪɭɝɢɦɢ ɫɥɨɜɚɦɢ, ɛɢɟɧɢɹ ɧɚɛɥɸɞɚɸɬɫɹ, ɟɫɥɢ ɡɚ ɨɞɢɧ ɩɟ-
ɪɢɨɞ ɢɡɦɟɧɟɧɢɹ ɚɦɩɥɢɬɭɞɵ ɬɟɥɨ ɫɨɜɟɪɲɚɟɬ ɦɧɨɝɨ ɤɨɥɟɛɚɧɢɣ.
ɑɚɫɬɧɵɣ ɫɥɭɱɚɣ, ɤɨɝɞɚ ɫɤɥɚɞɵɜɚɸɬɫɹ ɤɨɥɟɛɚɧɢɹ ɫ ɨɞɢɧɚɤɨɜɵɦɢ
ɚɦɩɥɢɬɭɞɚɦɢ
21
AA ( 0 M ), ɨɩɢɫɵɜɚɟɬɫɹ ɛɨɥɟɟ ɩɪɨɫɬɵɦɢ ɭɪɚɜɧɟɧɢɹ-
ɦɢ
)cos()(
0
MZ ttAx ,
ɝɞɟ
tAtAA Z' Z'
2
1
22
1
2
1
2
cos4))cos(1(2 ,
tAA Z'
2
1
1
cos2 .
ɂɡ ɩɪɢɜɟɞɟɧɧɵɯ ɜɵɪɚɠɟɧɢɣ ɜɢɞɧɨ, ɱɬɨ ɩɪɢ ɫɥɨɠɟɧɢɢ ɨɞɢɧɚɤɨɜɨ
ɧɚɩɪɚɜɥɟɧɧɵɯ ɝɚɪɦɨɧɢɱɟɫɤɢɯ ɤɨɥɟɛɚɧɢɣ ɫ ɨɞɢɧɚɤɨɜɵɦɢ ɚɦɩɥɢɬɭɞɚɦɢ
21
AA
ɢ ɛɥɢɡɤɢɦɢ ɱɚɫɬɨɬɚɦɢ
21
Z|Z
ɪɟɡɭɥɶɬɢɪɭɸɳɢɟ ɤɨɥɟɛɚɧɢɹ
(ɛɢɟɧɢɹ) ɫɨɜɟɪɲɚɸɬɫɹ ɫɨ ɫɪɟɞɧɟɣ ɱɚɫɬɨɬɨɣ
Z, ɩɪɢ ɷɬɨɦ ɚɦɩɥɢɬɭɞɚ ɤɨ-
ɥɟɛɚɧɢɣ ɦɟɞɥɟɧɧɨ ɦɟɧɹɟɬɫɹ ɫɨ ɜɪɟɦɟɧɟɦ ɨɬ ɧɭɥɹ ɞɨ
1
2A ɩɨ ɝɚɪɦɨɧɢɱɟ-
ɫɤɨɦɭ ɡɚɤɨɧɭ. ɑɚɫɬɨɬɚ ɛɢɟɧɢɣ ɪɚɜɧɚ ɩɨɥɨɜɢɧɟ ɪɚɡɧɨɫɬɢ ɱɚɫɬɨɬ ɫɤɥɚɞɵ-
ɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ
Z'
2
1
(ɪɢɫ. 3).
x
t
Ⱥ
Ɋɢɫ. 3

Ʉɨɥɟɛɚɧɢɹ ɢ ɜɨɥɧɵ
282
2. Ɋɚɛɨɱɢɟ ɮɨɪɦɭɥɵ
ɇɚɛɥɸɞɚɹ ɛɢɟɧɢɹ, ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɧɚɢɛɨɥɶɲɭɸ
max
A ɢ ɧɚɢ-
ɦɟɧɶɲɭɸ
min
A ɚɦɩɥɢɬɭɞɭ ɪɟɡɭɥɶɬɢɪɭɸɳɢɯ ɤɨɥɟɛɚɧɢɣ. ȿɫɥɢ ɦɢɧɢɦɚɥɶ-
ɧɚɹ ɚɦɩɥɢɬɭɞɚ
min
A ɨɬɥɢɱɧɚ ɨɬ ɧɭɥɹ, ɬɨ ɧɚɛɥɸɞɚɟɬɫɹ ɫɥɨɠɟɧɢɟ ɤɨɥɟɛɚ-
ɧɢɣ ɫ ɪɚɡɧɵɦɢ ɚɦɩɥɢɬɭɞɚɦɢ. Ȼɭɞɟɦ ɫɱɢɬɚɬɶ, ɱɬɨ ɚɦɩɥɢɬɭɞɚ ɩɟɪɜɨɝɨ ɤɨ-
ɥɟɛɚɧɢɹ ɛɨɥɶɲɟ
21
AA ! . Ɍɨɝɞɚ
21max
AAA ;
21min
AAA .
Ɉɬɫɸɞɚ ɥɟɝɤɨ ɨɩɪɟɞɟɥɢɬɶ ɚɦɩɥɢɬɭɞɵ ɫɤɥɚɞɵɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ
)(
minmax
2
1
1
AAA ; )(
minmax
2
1
2
AAA .
ɉɪɢ ɛɢɟɧɢɹɯ ɪɟɡɭɥɶɬɢɪɭɸɳɢɟ ɤɨɥɟɛɚɧɢɹ ɩɪɨɢɫɯɨɞɹɬ ɫ ɩɨɫɬɨɹɧ-
ɧɨɣ ɱɚɫɬɨɬɨɣ :. ɋ ɩɨɦɨɳɶɸ ɫɟɤɭɧɞɨɦɟɪɚ ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɩɟɪɢɨɞ ɢ
ɜɵɱɢɫɥɢɬɶ ɱɚɫɬɨɬɭ ɪɟɡɭɥɶɬɢɪɭɸɳɢɯ ɤɨɥɟɛɚɧɢɣ :. ȿɫɥɢ ɱɚɫɬɨɬɚ ɨɞɧɨɝɨ
ɢɡ ɤɨɥɟɛɚɧɢɣ, ɧɚɩɪɢɦɟɪ
2
Z , ɢɡɜɟɫɬɧɚ, ɬɨ ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɱɚɫɬɨɬɭ
ɞɪɭɝɨɝɨ ɤɨɥɟɛɚɧɢɹ
1
Z . Ⱦɥɹ ɷɬɨɝɨ ɜ ɜɵɪɚɠɟɧɢɢ ɞɥɹ : ɜɟɪɧɟɦɫɹ ɤ ɱɚɫɬɨ-
ɬɚɦ
1
Z ,
2
Z ɢ ɜɜɟɞɟɦ ɨɛɨɡɧɚɱɟɧɢɟ
21
21
AA
AA
A
G
:
)()(1
12
2
1
21
2
1
2
1
2
1
ZZGZZ Z'GZ
¸
¹
·
¨
©
§
Z
Z'
GZ|:
AAA
.
ɂɡ ɷɬɨɝɨ ɭɪɚɜɧɟɧɢɹ ɦɨɠɧɨ ɜɵɪɚɡɢɬɶ ɢɫɤɨɦɭɸ ɜɟɥɢɱɢɧɭ
1
Z ɱɟɪɟɡ
ɞɜɟ ɢɡɜɟɫɬɧɵɟ
2
Z ɢ ::
A
A
A
G
G
Z
G
:
Z
1
1
1
2
21
ɢɥɢ
1
2
2
1
21
1
A
A
A
AA
Z
: Z
.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɟɫɥɢ ɱɚɫɬɨɬɚ
2
Z ɨɞɧɨɝɨ ɢɡ ɫɤɥɚɞɵɜɚɟɦɵɯ ɤɨɥɟɛɚ-
ɧɢɣ ɢɡɜɟɫɬɧɚ, ɢɡɦɟɪɢɜ ɧɚɢɛɨɥɶɲɭɸ
max
A ɢ ɧɚɢɦɟɧɶɲɭɸ
min
A ɚɦɩɥɢɬɭ-
ɞɵ ɢ ɱɚɫɬɨɬɭ : ɫɭɦɦɚɪɧɵɯ ɤɨɥɟɛɚɧɢɣ, ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɩɚɪɚɦɟɬɪɵ
ɫɤɥɚɞɵɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ – ɚɦɩɥɢɬɭɞɵ
1
A ,
2
A ɢ ɧɟɢɡɜɟɫɬɧɭɸ ɱɚɫɬɨɬɭ
1
Z .
2.1. Ɂɚɜɢɫɢɦɨɫɬɶ ɯɚɪɚɤɬɟɪɚ ɪɟɡɭɥɶɬɢɪɭɸɳɟɝɨ ɞɜɢɠɟɧɢɹ
ɨɬ ɫɨɨɬɧɨɲɟɧɢɹ ɱɚɫɬɨɬ ɫɤɥɚɞɵɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ
Ʉɚɤ ɛɵɥɨ ɩɨɤɚɡɚɧɨ ɜɵɲɟ, ɛɢɟɧɢɹ ɧɚɛɥɸɞɚɸɬɫɹ ɬɨɥɶɤɨ ɩɪɢ ɨɩɪɟ-
ɞɟɥɟɧɧɨɦ ɫɨɨɬɧɨɲɟɧɢɢ ɱɚɫɬɨɬ. Ⱦɥɹ ɬɨɝɨ, ɱɬɨɛɵ ɨɩɪɟɞɟɥɢɬɶ ɜ ɤɚɤɨɦ
ɞɢɚɩɚɡɨɧɟ ɱɚɫɬɨɬ ɦɨɠɧɨ ɧɚɛɥɸɞɚɬɶ ɛɢɟɧɢɹ, ɪɚɫɫɦɨɬɪɢɦ, ɤɚɤ ɦɟɧɹɟɬɫɹ

ɆɨɞɄ-05 ɋɥɨɠɟɧɢɟ ɤɨɥɟɛɚɧɢɣ. Ȼɢɟɧɢɹ
283
ɯɚɪɚɤɬɟɪ ɪɟɡɭɥɶɬɢɪɭɸɳɟɝɨ ɞɜɢɠɟɧɢɹ ɨɬ ɫɨɨɬɧɨɲɟɧɢɹ ɱɚɫɬɨɬ ɫɤɥɚɞɵ-
ɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ.
Ȼɵɥɨ ɩɨɤɚɡɚɧɨ, ɱɬɨ ɧɚɱɚɥɶɧɚɹ ɮɚɡɚ ɫɤɥɚɞɵɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ ɧɟ
ɜɥɢɹɟɬ ɧɚ ɱɚɫɬɨɬɭ ɢ ɚɦɩɥɢɬɭɞɭ ɪɟɡɭɥɶɬɢɪɭɸɳɢɯ ɤɨɥɟɛɚɧɢɣ. ɉɨɷɬɨɦɭ ɡɚ
ɧɚɱɚɥɨ ɨɬɫɱɟɬɚ ɜɪɟɦɟɧɢ ɩɪɢɦɟɦ ɦɨɦɟɧɬ
0
t
, ɤɨɝɞɚ ɮɚɡɵ ɨɛɨɢɯ ɫɤɥɚɞɵ-
ɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ
1
x ɢ
2
x ɫɨɜɩɚɞɚɸɬ; ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ ɪɚɫɩɨɥɨɠɢɦ
ɬɚɤ, ɱɬɨɛɵ ɧɚɱɚɥɶɧɚɹ ɮɚɡɚ ɛɵɥɚ ɪɚɜɧɚ ɧɭɥɸ.
Ɍɨɝɞɚ ɡɚɤɨɧ ɢɡɦɟɧɟɧɢɹ ɪɟɡɭɥɶɬɢɪɭɸɳɟɝɨ ɞɜɢɠɟɧɢɹ ɦɨɠɧɨ ɡɚɩɢ-
ɫɚɬɶ ɞɜɭɦɹ ɫɩɨɫɨɛɚɦɢ:
)cos()cos(
2211
tAtAx ZZ ,
ɥɢɛɨ
))(cos()( tttA
x
MZ ,
t
AA
AA
Z'
M
2
1
21
12
tgtg
,
)cos(2
21
2
2
2
1
2
tAAAAA Z' .
ȼɵɛɨɪ ɫɩɨɫɨɛɚ ɡɚɩɢɫɢ ɡɚɤɨɧɚ ɪɟɡɭɥɶɬɢɪɭɸɳɟɝɨ ɞɜɢɠɟɧɢɹ ɫɜɹɡɚɧ
ɫ ɭɞɨɛɫɬɜɨɦ ɚɧɚɥɢɡɚ ɯɚɪɚɤɬɟɪɚ ɞɜɢɠɟɧɢɹ.
Ɂɚɮɢɤɫɢɪɭɟɦ ɱɚɫɬɨɬɭ
1
Z
ɩɟɪɜɨɝɨ ɤɨɥɟɛɚɧɢɹ. Ɋɚɫɫɦɨɬɪɢɦ, ɤɚɤ ɢɡ-
ɦɟɧɢɬɫɹ ɯɚɪɚɤɬɟɪ ɪɟɡɭɥɶɬɢɪɭɸɳɟɝɨ ɞɜɢɠɟɧɢɹ ɜ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɱɚɫɬɨɬɵ
ɜɬɨɪɨɝɨ ɤɨɥɟɛɚɧɢɹ
2
Z .
1.
0
2
Z ( Z Z' ).
ɍɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ
211
)cos( AtAx Z .
ȼɵɜɨɞ:
ɝɚɪɦɨɧɢɱɟɫɤɨɟ ɞɜɢɠɟɧɢɟ ɫ
ɩɨɫɬɨɹɧɧɨɣ ɱɚɫɬɨɬɨɣ
1
Z
ɢ ɫ ɩɨɫɬɨ-
ɹɧɧɨɣ ɚɦɩɥɢɬɭɞɨɣ, ɩɨɥɨɠɟɧɢɟ
ɪɚɜɧɨɜɟɫɢɹ ɤɨɬɨɪɨɝɨ ɩɨɞɧɹɬɨ ɧɚ
ɜɟɥɢɱɢɧɭ
2
A .
x
t
A
2
+A
1
A
2
– A
1
A
2
Ʉɨɥɟɛɚɧɢɹ ɢ ɜɨɥɧɵ
284
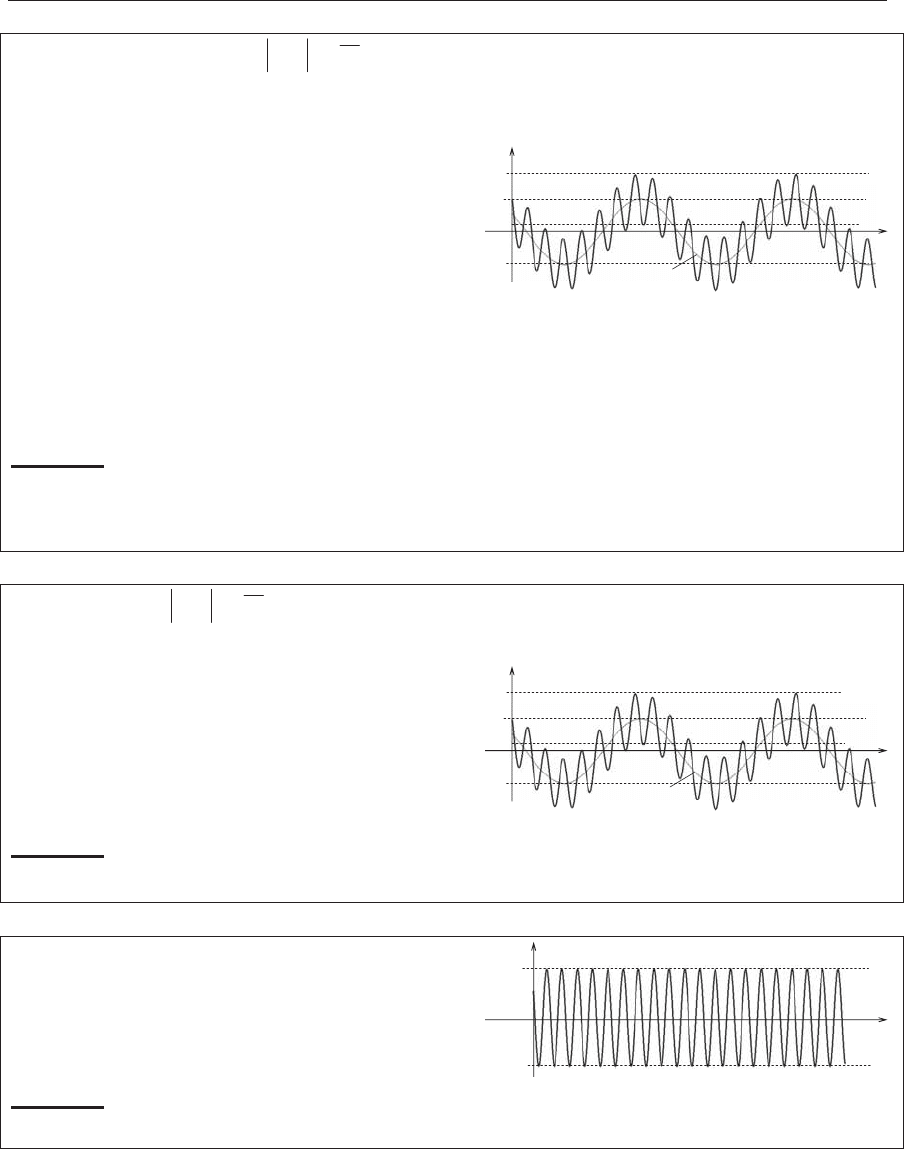
2.
0
2
!Z ,
12
ZZ ( Z|Z' ).
ɍɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ
)cos()cos(
2211
tAtAx ZZ .
ɉɟɪɢɨɞ ɩɟɪɜɨɝɨ ɤɨɥɟɛɚɧɢɹ ɦɧɨɝɨ
ɦɟɧɶɲɟ ɩɟɪɢɨɞɚ ɜɬɨɪɨɝɨ ɤɨɥɟɛɚ-
ɧɢɹ. ȼ ɬɟɱɟɧɢɟ ɩɟɪɢɨɞɚ ɩɟɪɜɨɝɨ
ɤɨɥɟɛɚɧɢɹ ɜɬɨɪɨɟ ɤɨɥɟɛɚɧɢɟ ɦɟɧɹ-
ɟɬɫɹ ɧɟɡɧɚɱɢɬɟɥɶɧɨ. ȼ ɬɟɱɟɧɢɟ ɤɚ-
ɠɞɨɝɨ ɩɟɪɢɨɞɚ ɩɟɪɜɨɝɨ ɤɨɥɟɛɚɧɢɹ ɪɟɡɭɥɶɬɢɪɭɸɳɟɟ ɞɜɢɠɟɧɢɟ ɦɨɠɧɨ
ɪɚɫɫɦɚɬɪɢɜɚɬɶ, ɤɚɤ ɝɚɪɦɨɧɢɱɟɫɤɨɟ ɫɨ ɫɦɟɳɟɧɧɵɦ ɩɨɥɨɠɟɧɢɟɦ ɪɚɜɧɨɜɟ-
ɫɢɹ (ɫɥɭɱɚɣ 1). Ɉɞɧɚɤɨ ɨɬ ɩɟɪɢɨɞɚ ɤ ɩɟɪɢɨɞɭ ɫɦɟɳɟɧɢɟ ɩɨɥɨɠɟɧɢɹ ɪɚɜ-
ɧɨɜɟɫɢɹ ɦɟɧɹɟɬɫɹ.
ȼɵɜɨɞ:
ɝɚɪɦɨɧɢɱɟɫɤɨɟ ɞɜɢɠɟɧɢɟ ɫ ɩɨɫɬɨɹɧɧɨɣ ɱɚɫɬɨɬɨɣ
1
Z , ɩɨɥɨɠɟɧɢɟ
ɪɚɜɧɨɜɟɫɢɹ ɤɨɬɨɪɨɝɨ ɤɨɥɟɛɥɟɬɫɹ ɩɨ ɝɚɪɦɨɧɢɱɟɫɤɨɦɭ ɡɚɤɨɧɭ ɨɬ –
2
A ɞɨ
2
A .
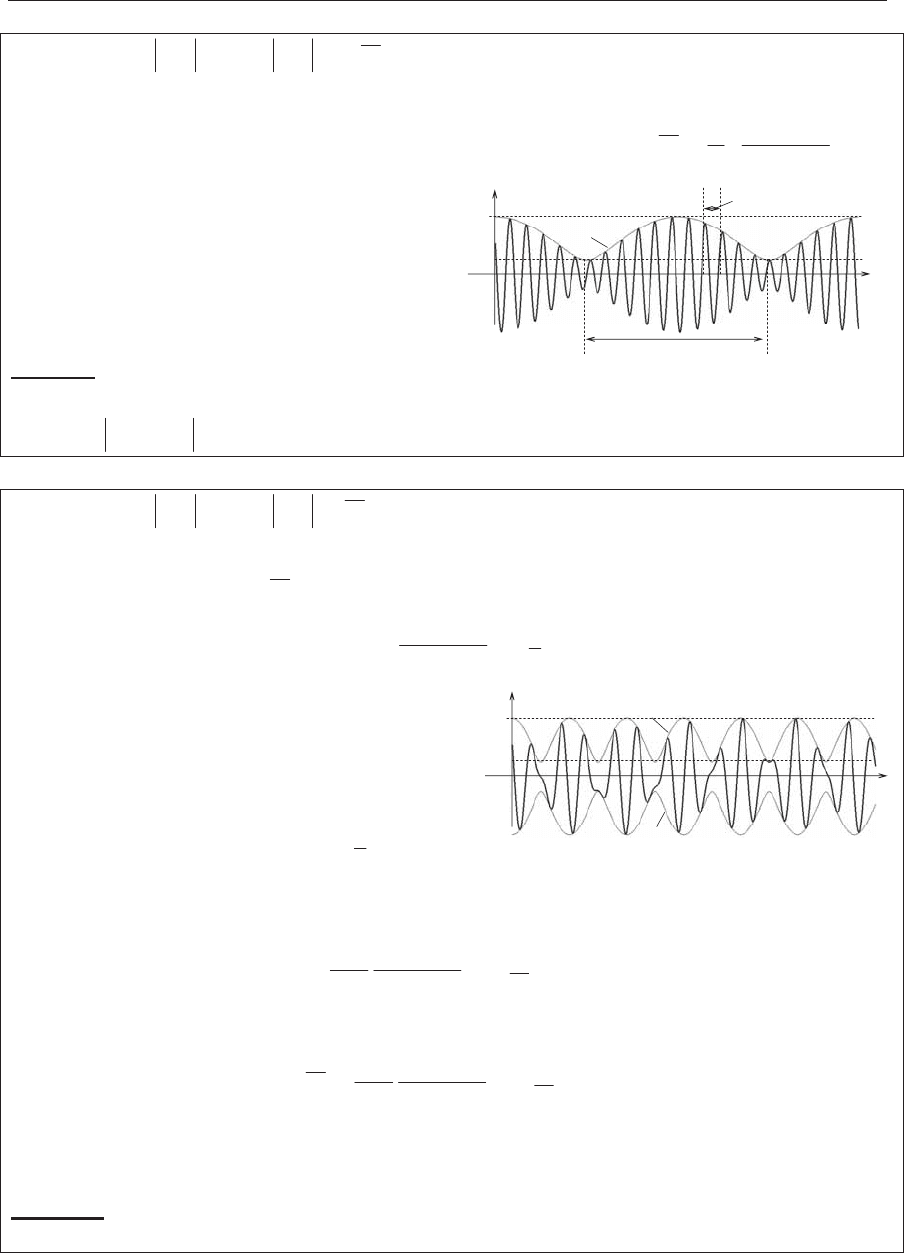
3.
12
Z!!Z ( Z|Z' ).
ɍɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ
)cos()cos(
2211
tAtAx ZZ .
ɉɟɪɢɨɞ ɜɬɨɪɨɝɨ ɤɨɥɟɛɚɧɢɹ ɦɧɨɝɨ
ɦɟɧɶɲɟ ɩɟɪɢɨɞɚ ɩɟɪɜɨɝɨ ɤɨɥɟɛɚ-
ɧɢɹ. ɋɥɭɱɚɣ ɩɪɨɬɢɜɨɩɨɥɨɠɧɵɣ
ɫɥɭɱɚɸ 2.
ȼɵɜɨɞ:
ɝɚɪɦɨɧɢɱɟɫɤɨɟ ɞɜɢɠɟɧɢɟ ɫ ɩɨɫɬɨɹɧɧɨɣ ɱɚɫɬɨɬɨɣ
2
Z , ɩɨɥɨɠɟɧɢɟ
ɪɚɜɧɨɜɟɫɢɹ ɤɨɬɨɪɨɝɨ ɤɨɥɟɛɥɟɬɫɹ ɩɨ ɝɚɪɦɨɧɢɱɟɫɤɨɦɭ ɡɚɤɨɧɭ ɨɬ –
1
A ɞɨ
1
A .
4.
12
Z Z
(
0 Z'
).
ɍɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ
)cos()(
121
tAAx Z .
ɋɥɨɠɟɧɢɟ ɤɨɝɟɪɟɧɬɧɵɯ ɤɨɥɟɛɚɧɢɣ.
ȼɵɜɨɞ:
ɝɚɪɦɨɧɢɱɟɫɤɨɟ ɞɜɢɠɟɧɢɟ ɫ
ɩɨɫɬɨɹɧɧɨɣ ɱɚɫɬɨɬɨɣ
1
Z ɢ ɩɨɫɬɨɹɧɧɨɣ ɚɦɩɥɢɬɭɞɨɣ
21
AA .
x
t
A
2
+A
1
A
2
– A
1
x
2
A
2
–A
2
x
t
A
1
+A
2
A
1
– A
2
x
1
A
1
–A
1
x
t
A
1
+A
2
–(A
1
+ A
2
)
ɆɨɞɄ-05 ɋɥɨɠɟɧɢɟ ɤɨɥɟɛɚɧɢɣ. Ȼɢɟɧɢɹ
285
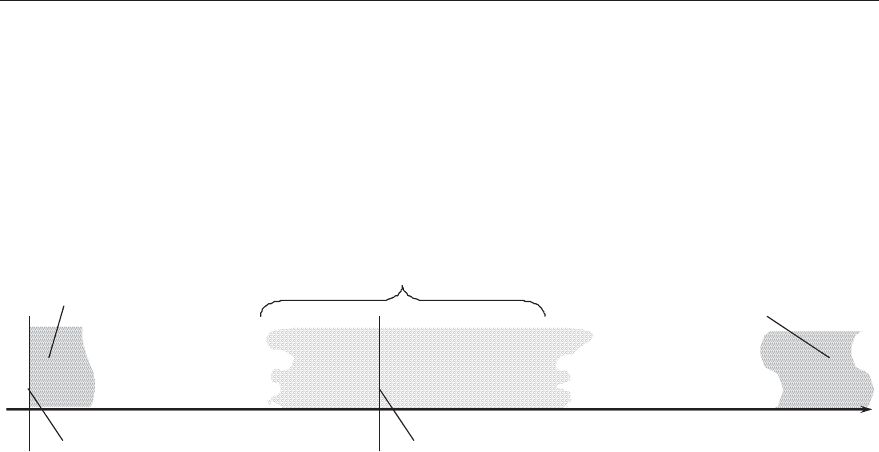
5.
12
Z|Z ( 0zZ' ), ZZ' .
ɍɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ
)cos()( ttA
x
:
,
)cos(2
21
2
2
2
1
2
tAAAAA Z'
, Z'
Z|:
21
12
2
1
AA
AA
.
ɑɚɫɬɨɬɚ, ɚ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɢ ɩɟ-
ɪɢɨɞ ɪɟɡɭɥɶɬɢɪɭɸɳɢɯ ɤɨɥɟɛɚɧɢɣ
ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɜɪɟɦɟɧɢ. ɉɟɪɢɨɞ
ɢɡɦɟɧɟɧɢɹ ɚɦɩɥɢɬɭɞɵ ɦɧɨɝɨ
ɛɨɥɶɲɟ ɩɟɪɢɨɞɚ ɤɨɥɟɛɚɧɢɣ.
ȼɵɜɨɞ
: ɛɢɟɧɢɹ – ɝɚɪɦɨɧɢɱɟɫɤɨɟ
ɞɜɢɠɟɧɢɟ ɫ ɩɨɫɬɨɹɧɧɨɣ ɱɚɫɬɨɬɨɣ :, ɚɦɩɥɢɬɭɞɚ ɤɨɬɨɪɨɝɨ ɦɟɞɥɟɧɧɨ ɦɟɧɹ-
ɟɬɫɹ ɨɬ
21
AA ɞɨ
21
AA .
6.
12
ZzZ ( 0zZ' ), ZZ' .
ɍɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ
))(cos()( tttA
x
MZ
, )cos(2
21
2
2
2
1
2
tAAAAA Z' ,
t
AA
AA
t Z'
M
2
1
21
12
tg)(tg .
Ɋɚɡɧɨɫɬɶ ɱɚɫɬɨɬ ɧɟ ɛɟɫɤɨɧɟɱɧɨ ɦɚ-
ɥɚɹ ɜɟɥɢɱɢɧɚ, ɩɨɷɬɨɦɭ ɞɥɹ ɨɩɪɟɞɟ-
ɥɟɧɢɹ ɞɨɩɨɥɧɢɬɟɥɶɧɨɣ ɮɚɡɵ
)(tM
ɧɟ ɞɨɫɬɚɬɨɱɧɨ ɨɞɧɨɝɨ ɱɥɟɧɚ ɜ ɪɚɡ-
ɥɨɠɟɧɢɢ ɜ ɪɹɞ ɬɚɧɝɟɧɫɚ
tZ'
2
1
tg .
Ɋɚɡɥɨɠɟɧɢɟ ɬɚɧɝɟɧɫɚ ɜ ɪɹɞ ɞɨ ɜɬɨɪɨɝɨ ɩɨɪɹɞɤɚ ɦɚɥɨɫɬɢ ɩɨɡɜɨɥɹɟɬ ɩɨɥɭ-
ɱɢɬɶ ɞɨɩɨɥɧɢɬɟɥɶɧɭɸ ɮɚɡɭ ɜ ɜɢɞɟ
tt
AA
AA
t Z'
Z'
|M
2
(
12
1
21
12
)1
2
)( .
Ɍɨ ɟɫɬɶ ɱɚɫɬɨɬɚ ɤɨɥɟɛɚɧɢɣ : ɡɚɜɢɫɢɬ ɨɬ ɜɪɟɦɟɧɢ
2
(
12
1
21
12
)1
2
t
AA
AA
Z'
Z'
Z|: .
ɉɟɪɢɨɞ ɢɡɦɟɧɟɧɢɹ ɚɦɩɥɢɬɭɞɵ ɧɟɡɧɚɱɢɬɟɥɶɧɨ ɛɨɥɶɲɟ ɩɟɪɢɨɞɚ ɤɨɥɟɛɚ-
ɧɢɣ.
ȼɵɜɨɞ:
ɞɜɢɠɟɧɢɟ ɫ ɩɟɪɟɦɟɧɧɨɣ ɱɚɫɬɨɬɨɣ ɢ ɩɟɪɟɦɟɧɧɨɣ ɚɦɩɥɢɬɭɞɨɣ –
ɧɟɝɚɪɦɨɧɢɱɟɫɤɨɟ ɞɜɢɠɟɧɢɟ.
x
t
A
1
+A
2
_A
1
– A
2
_
A
2S
/
'Z
2S
/
:
x
t
A
1
+A
2
_
A
1
– A
2
_
–A
A
Ʉɨɥɟɛɚɧɢɹ ɢ ɜɨɥɧɵ
286
Ɉɩɢɫɚɧɧɵɟ ɫɥɭɱɚɢ ɧɟ ɢɦɟɸɬ ɱɟɬɤɨ ɜɵɪɚɠɟɧɧɵɯ ɝɪɚɧɢɰ ɧɚ ɲɤɚɥɟ
ɱɚɫɬɨɬ, ɚ ɩɥɚɜɧɨ ɩɟɪɟɯɨɞɹɬ ɨɞɢɧ ɜ ɞɪɭɝɨɣ (ɪɢɫ. 4). ȼɫɟ ɨɛɥɚɫɬɢ ɱɚɫɬɨɬ, ɜ
ɤɨɬɨɪɵɯ ɧɚɛɥɸɞɚɟɬɫɹ ɞɜɢɠɟɧɢɟ ɨɞɧɨɝɨ ɜɢɞɚ, ɪɚɫɩɨɥɨɠɟɧɵ ɤɚɤ ɫɩɪɚɜɚ,
ɬɚɤ ɢ ɫɥɟɜɚ ɨɬ ɡɚɮɢɤɫɢɪɨɜɚɧɧɨɣ ɱɚɫɬɨɬɵ
1
Z . ɉɪɨɬɹɠɟɧɧɨɫɬɶ ɨɛɥɚɫɬɟɣ ɫ
ɨɞɢɧɚɤɨɜɵɦ ɯɚɪɚɤɬɟɪɨɦ ɞɜɢɠɟɧɢɹ ɧɟ ɨɞɢɧɚɤɨɜɚ ɫɩɪɚɜɚ ɢ ɫɥɟɜɚ ɨɬ ɡɚ-
ɮɢɤɫɢɪɨɜɚɧɧɨɣ ɱɚɫɬɨɬɵ
1
Z ɢ ɡɚɜɢɫɹɬ ɨɬ ɡɧɚɱɟɧɢɹ ɷɬɨɣ ɱɚɫɬɨɬɵ.
Z
1
Z
2
0
Ȼɢɟɧɢɹ
ɇɟɝɚɪɦɨɧɢɱɟɫɤɢɟ
ɤɨɥɟɛɚɧɢɹ
ɇɟɝɚɪɦɨɧɢɱɟɫɤɢɟ
ɤɨɥɟɛɚɧɢɹ
Ʉɨɥɟɛɚɧɢɹ ɫ ɩɟɪɟɦɟɧɧɵɦ
ɩɨɥ ɨɠɟɧɢɟɦ ɪɚɜɧɨɜɟɫɢɹ
Ʉɨɥɟɛɚɧɢɹ ɫ ɩɟɪɟɦɟɧɧɵɦ
ɩɨɥɨɠɟɧɢɟɦ ɪɚɜɧɨɜɟɫɢɹ
Ƚɚɪɦɨɧɢɱɟɫɤɢɟ
ɤɨɥɟɛɚɧɢɹ
Ƚɚɪɦɨɧɢɱɟɫɤɢɟ
ɤɨɥɟɛɚɧɢɹ
Ɋɢɫ. 4
3. Ɇɨɞɟɥɶ ɷɤɫɩɟɪɢɦɟɧɬɚɥɶɧɨɣ ɭɫɬɚɧɨɜɤɢ
ȼ ɞɚɧɧɨɣ ɪɚɛɨɬɟ ɫ ɩɨɦɨɳɶɸ ɫɪɟɞɫɬɜ ɤɨɦɩɶɸɬɟɪɧɨɣ ɝɪɚɮɢɤɢ ɦɨ-
ɞɟɥɢɪɭɟɬɫɹ ɩɪɨɰɟɫɫ ɫɥɨɠɟɧɢɹ ɞɜɭɯ ɝɚɪɦɨɧɢɱɟɫɤɢɯ ɤɨɥɟɛɚɧɢɣ: ɫɨɛɫɬ-
ɜɟɧɧɵɯ ɤɨɥɟɛɚɧɢɣ ɩɪɭɠɢɧɧɨɝɨ ɦɚɹɬɧɢɤɚ ɩɨ ɡɚɤɨɧɭ
)cos(
111
tAx Z ɢ
ɝɚɪɦɨɧɢɱɟɫɤɢɯ ɤɨɥɟɛɚɧɢɣ ɜɧɟɲɧɟɣ ɫɢɥɵ ɩɨ ɡɚɤɨɧɭ
)cos(
222
tAx Z
(
21
AA ! ). Ɉɛɚ ɤɨɥɟɛɚɧɢɹ ɫɨɜɟɪɲɚɸɬɫɹ ɜ ɨɞɧɨɦ ɧɚɩɪɚɜɥɟɧɢɢ. ɋɨɩɪɨ-
ɬɢɜɥɟɧɢɟ ɫɪɟɞɵ ɨɬɫɭɬɫɬɜɭɟɬ. ɋɢɥɚ ɬɹɠɟɫɬɢ ɢ ɜɫɟ ɤɨɦɩɟɧɫɢɪɭɸɳɢɟ ɟɟ
ɫɢɥɵ ɧɚɩɪɚɜɥɟɧɵ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨ ɧɚɩɪɚɜɥɟɧɢɸ ɞɜɢɠɟɧɢɹ ɦɚɹɬɧɢɤɚ
(ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨ ɩɥɨɫɤɨɫɬɢ ɷɤɪɚɧɚ) ɢ ɧɟ ɨɤɚɡɵɜɚɟɬ ɜɥɢɹɧɢɹ ɧɚ ɞɜɢɠɟ-
ɧɢɟ.
ȼɵɧɭɠɞɚɸɳɚɹ ɫɢɥɚ ɜ ɪɚɛɨɬɟ ɢɡɨɛɪɚɠɟɧɚ ɜ ɜɢɞɟ ɜɟɪɬɢɤɚɥɶɧɨɝɨ
ɦɟɬɚɥɥɢɱɟɫɤɨɝɨ ɫɬɟɪɠɧɹ, ɤɨɬɨɪɵɣ ɦɨɠɟɬ ɞɜɢɝɚɬɶɫɹ ɜ ɜɟɪɬɢɤɚɥɶɧɨɦ ɧɚ-
ɩɪɚɜɥɟɧɢɢ
ɩɨ ɝɚɪɦɨɧɢɱɟɫɤɨɦɭ ɡɚɤɨɧɭ ɫ ɪɚɡɥɢɱɧɵɦɢ ɱɚɫɬɨɬɚɦɢ. ɉɪɭ-
ɠɢɧɧɵɣ ɦɚɹɬɧɢɤ ɩɪɢɫɨɟɞɢɧɟɧ ɤ ɧɢɠɧɟɦɭ ɬɨɪɰɭ ɫɬɟɪɠɧɹ. Ⱦɥɹ ɬɨɝɨ ɱɬɨ-
ɛɵ ɫɬɟɪɠɟɧɶ ɦɨɝ ɤɨɥɟɛɚɬɶɫɹ ɫ ɪɚɡɥɢɱɧɵɦɢ ɱɚɫɬɨɬɚɦɢ ɛɟɡ ɩɨɬɟɪɢ ɷɧɟɪ-
ɝɢɢ, ɨɧ ɞɨɥɠɟɧ ɩɪɢɜɨɞɢɬɶɫɹ ɜ ɞɜɢɠɟɧɢɟ ɤɚɤɢɦ-ɥɢɛɨ ɦɟɯɚɧɢɡɦɨɦ. ɍɫɬ-
ɪɨɣɫɬɜɨ ɦɟɯɚɧɢɡɦɚ ɦɨɠɟɬ ɛɵɬɶ ɪɚɡɥɢɱɧɵɦ. Ʉɨɥɟɛɚɧɢɹ ɫɬɟɪɠɧɹ ɦɨɝɭɬ
ɝɟɧɟɪɢɪɨɜɚɬɶɫɹ, ɧɚɩɪɢɦɟɪ, ɷɥɟɤɬɪɨɦɚɝɧɢɬɨɦ, ɪɚɜɧɨɦɟɪɧɨ ɜɪɚɳɚɸɳɢɦɫɹ
ɞɢɫɤɨɦ
ɢɥɢ ɤɚɤɢɦ-ɥɢɛɨ ɞɪɭɝɢɦ ɫɩɨɫɨɛɨɦ. ɏɚɪɚɤɬɟɪ ɭɫɬɪɨɣɫɬɜɚ, ɫɨɡ-
ɞɚɸɳɟɝɨ ɜɧɟɲɧɸɸ ɫɢɥɭ, ɧɟ ɨɤɚɡɵɜɚɟɬ ɜɥɢɹɧɢɹ ɧɚ ɩɪɨɰɟɫɫ ɫɥɨɠɟɧɢɹ
ɤɨɥɟɛɚɧɢɣ. ɉɨɷɬɨɦɭ ɜɧɟɲɧɢɣ ɜɢɞ ɭɫɬɪɨɣɫɬɜɚ, ɡɚɫɬɚɜɥɹɸɳɟɝɨ ɫɬɟɪɠɟɧɶ
ɆɨɞɄ-05 ɋɥɨɠɟɧɢɟ ɤɨɥɟɛɚɧɢɣ. Ȼɢɟɧɢɹ
287
ɞɜɢɝɚɬɶɫɹ ɝɚɪɦɨɧɢɱɟɫɤɢ, ɜ ɪɚɛɨɬɟ ɧɟ ɩɪɢɜɨɞɢɬɫɹ (ɢɡɭɱɟɧɢɟ ɭɫɬɪɨɣɫɬɜɚ
ɧɟ ɹɜɥɹɟɬɫɹ ɰɟɥɶɸ ɪɚɛɨɬɵ). Ɉɞɧɚɤɨ, ɭɫɬɪɨɣɫɬɜɨ ɬɚɤɨɜɨ, ɱɬɨ ɜɧɟɲɧɹɹ ɫɢ-
ɥɚ ɫɨɜɟɪɲɚɟɬ ɝɚɪɦɨɧɢɱɟɫɤɢɟ ɤɨɥɟɛɚɧɢɹ ɩɨ ɡɚɤɨɧɭ
)cos(
222
tAx Z ɜ ɬɨɦ
ɠɟ ɧɚɩɪɚɜɥɟɧɢɢ, ɱɬɨ ɢ ɩɪɭɠɢɧɧɵɣ ɦɚɹɬɧɢɤ. ɑɚɫɬɨɬɚ ɜɵɧɭɠɞɚɸɳɟɣ ɫɢ-
ɥɵ ɞɥɹ ɪɚɡɥɢɱɧɵɯ ɨɩɵɬɨɜ ɦɨɠɟɬ ɛɵɬɶ ɜɵɛɪɚɧɚ ɢɡ ɞɢɚɩɚɡɨɧɚ 0 – 6 ɪɚɞ/ɫ
ɢ ɧɟ ɦɨɠɟɬ ɛɵɬɶ ɢɡɦɟɧɟɧɚ ɜɨ ɜɪɟɦɹ ɩɪɨɜɟɞɟɧɢɹ ɨɩɵɬɚ.
Ⱦɥɹ ɨɩɪɟɞɟɥɟɧɢɹ ɚɦɩɥɢɬɭɞɵ ɪɟɡɭɥɶɬɢɪɭɸɳɢɯ ɤɨɥɟɛɚɧɢɣ ɜ ɪɚɛɨɬɟ
ɢɫɩɨɥɶɡɭɟɬɫɹ ɢɡɦɟɪɢɬɟɥɶɧɵɣ ɩɪɢɛɨɪ, ɫɩɨɫɨɛɧɵɣ ɢɡɦɟɪɹɬɶ ɤɨɨɪɞɢɧɚɬɭ ɫ
ɬɨɱɧɨɫɬɶɸ ɞɨ 0,5 ɦɦ. ɂɡɦɟɧɹɬɶ ɱɚɫɬɨɬɭ ɜɧɟɲɧɟɣ ɫɢɥɵ ɦɨɠɧɨ ɜ ɞɢɚɩɚ-
ɡɨɧɟ ɨɬ 0 ɞɨ 6 ɪɚɞ/ɫ ɫ ɬɨɱɧɨɫɬɶɸ 0,01 ɪɚɞ/ɫ. Ⱦɥɹ ɨɩɪɟɞɟɥɟɧɢɹ ɜɪɟɦɟɧɢ, ɡɚ
ɤɨɬɨɪɨɟ ɦɚɹɬɧɢɤ ɫɨɜɟɪɲɚɟɬ ɡɚɞɚɧɧɨɟ ɤɨɥɢɱɟɫɬɜɨ ɤɨɥɟɛɚɧɢɣ, ɢɫɩɨɥɶɡɭ-
ɟɬɫɹ ɫɟɤɭɧɞɨɦɟɪ, ɫɩɨɫɨɛɧɵɣ ɢɡɦɟɪɹɬɶ ɜɪɟɦɹ ɫ
ɬɨɱɧɨɫɬɶɸ ɞɨ 1 ɦɢɥɥɢɫɟ-
ɤɭɧɞɵ. ɉɪɢ ɭɤɚɡɚɧɧɵɯ ɭɫɥɨɜɢɹɯ ɩɨɝɪɟɲɧɨɫɬɶ ɨɩɪɟɞɟɥɟɧɢɹ ɚɦɩɥɢɬɭɞɵ
ɫɨɛɫɬɜɟɧɧɵɯ ɤɨɥɟɛɚɧɢɣ ɢ ɚɦɩɥɢɬɭɞɵ ɜɧɟɲɧɟɣ ɫɢɥɵ ɜ ɷɤɫɩɟɪɢɦɟɧɬɟ ɧɟ
ɩɪɟɜɵɲɚɟɬ 2,0–3,5 %, ɚ ɩɨɝɪɟɲɧɨɫɬɶ ɨɩɪɟɞɟɥɟɧɢɹ ɱɚɫɬɨɬɵ ɫɨɛɫɬɜɟɧɧɵɯ
ɤɨɥɟɛɚɧɢɣ ɜ ɷɤɫɩɟɪɢɦɟɧɬɟ ɧɟ ɩɪɟɜɵɲɚɟɬ 8–10 %.
Ɋɚɛɨɬɚ ɜɵɩɨɥɧɹɟɬɫɹ ɧɚ IBM-ɫɨɜɦɟɫɬɢɦɨɦ ɩɟɪɫɨɧɚɥɶɧɨɦ ɤɨɦɩɶɸ-
ɬɟɪɟ ɜ ɜɢɞɟ ɫɚɦɨɫɬɨɹɬɟɥɶɧɨɝɨ Windows-ɩɪɢɥɨɠɟɧɢɹ. Ⱦɥɹ ɭɞɨɛɫɬɜɚ ɜɵ-
ɩɨɥɧɟɧɢɹ ɪɚɛɨɬɵ ɜ ɩɪɨɝɪɚɦɦɟ ɩɪɟɞɭɫɦɨɬɪɟɧɵ ɬɪɢ ɪɚɡɞɟɥɚ
: ɤɪɚɬɤɨɟ ɨɩɢ-

Ʉɨɥɟɛɚɧɢɹ ɢ ɜɨɥɧɵ
288
ɫɚɧɢɟ ɪɚɛɨɬɵ; ɩɨɪɹɞɨɤ ɜɵɩɨɥɧɟɧɢɹ ɪɚɛɨɬɵ ɢ ɷɤɫɩɟɪɢɦɟɧɬ. ɉɟɪɟɤɥɸɱɟ-
ɧɢɟ ɦɟɠɞɭ ɪɚɡɞɟɥɚɦɢ ɨɫɭɳɟɫɬɜɥɹɟɬɫɹ ɫ ɩɨɦɨɳɶɸ ɤɧɨɩɨɤ «ɏɨɞ ɪɚɛɨɬɵ»
ɢ «ɗɤɫɩɟɪɢɦɟɧɬ». ɇɚɠɚɬɢɟ ɷɬɢɯ ɤɧɨɩɨɤ ɜ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɤɨɧɬɟɤɫɬɚ ɪɚ-
ɛɨɬɵ ɩɪɨɝɪɚɦɦɵ ɩɪɢɜɨɞɢɬ ɥɢɛɨ ɤ ɜɵɡɨɜɭ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ ɪɚɡɞɟɥɨɜ,
ɥɢɛɨ ɤ ɜɨɡɜɪɚɳɟɧɢɸ ɜ ɪɚɡɞɟɥ ɨɩɢɫɚɧɢɹ.
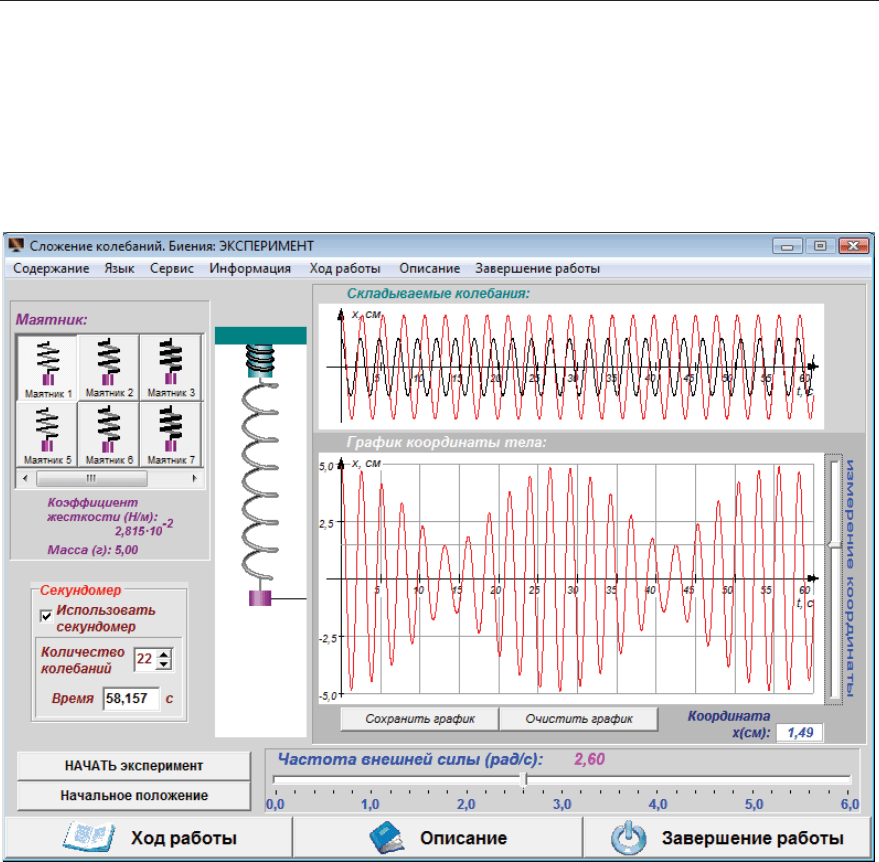
Ɋɚɡɞɟɥ ɩɪɨɝɪɚɦɦɵ «ɗɤɫɩɟɪɢɦɟɧɬ» ɫɨɞɟɪɠɢɬ ɛɟɝɭɧɨɤ ɩɪɨɤɪɭɬɤɢ
ɞɥɹ ɢɡɦɟɧɟɧɢɹ ɱɚɫɬɨɬɵ
ɜɧɟɲɧɟɣ ɫɢɥɵ, ɩɚɧɟɥɶ ɢɧɫɬɪɭɦɟɧɬɨɜ ɫ ɤɧɨɩɤɚɦɢ
ɞɥɹ ɜɵɛɨɪɚ ɦɚɹɬɧɢɤɚ, ɫɟɤɭɧɞɨɦɟɪ ɞɥɹ ɢɡɦɟɪɟɧɢɹ ɜɪɟɦɟɧɢ ɞɜɢɠɟɧɢɹ ɦɚ-
ɹɬɧɢɤɚ, ɛɟɝɭɧɨɤ ɩɪɨɤɪɭɬɤɢ ɞɥɹ ɢɡɦɟɪɟɧɢɹ ɤɨɨɪɞɢɧɚɬɵ ɦɚɹɬɧɢɤɚ, ɚ ɬɚɤ-
ɠɟ ɜɫɩɨɦɨɝɚɬɟɥɶɧɵɟ ɤɧɨɩɤɢ ɢ ɩɟɪɟɤɥɸɱɚɬɟɥɶ, ɩɨɡɜɨɥɹɸɳɢɣ ɪɟɝɭɥɢɪɨ-
ɜɚɬɶ ɢɫɩɨɥɶɡɨɜɚɧɢɟ ɫɟɤɭɧɞɨɦɟɪɚ.
ȼɚɪɢɚɧɬɵ ɜɵɩɨɥɧɟɧɢɹ ɪɚɛɨɬɵ
ʋ ɜɚɪɢɚɧɬɚ ʋ ɜɚɪɢɚɧɬɚ
1. Ɇɚɹɬɧɢɤ 1 5. Ɇɚɹɬɧɢɤ 5
2. Ɇɚɹɬɧɢɤ 2 6. Ɇɚɹɬɧɢɤ 6
3. Ɇɚɹɬɧɢɤ 3 7. Ɇɚɹɬɧɢɤ 7
4. Ɇɚɹɬɧɢɤ 4 8. Ɇɚɹɬɧɢɤ 8
4. ɉɨɪɹɞɨɤ ɜɵɩɨɥɧɟɧɢɹ ɪɚɛɨɬɵ
4.1. Ʉɪɚɬɤɨɟ ɨɩɢɫɚɧɢɟ ɯɨɞɚ ɪɚɛɨɬɵ
1. ȼɵɛɟɪɢɬɟ ɦɚɹɬɧɢɤ (ɩɨ ɭɤɚɡɚɧɢɸ ɩɪɟɩɨɞɚɜɚɬɟɥɹ).
2. ɍɫɬɚɧɨɜɢɬɟ ɦɢɧɢɦɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɱɚɫɬɨɬɵ ɜɧɟɲɧɟɣ ɫɢɥɵ.
3. ɉɨɫɬɪɨɣɬɟ ɝɪɚɮɢɤ ɤɨɨɪɞɢɧɚɬɵ ɬɟɥɚ.
4. Ɉɩɪɟɞɟɥɢɬɟ, ɤ ɤɚɤɨɦɭ ɬɢɩɭ ɨɬɧɨɫɢɬɫɹ ɞɚɧɧɨɟ ɤɨɥɟɛɚɬɟɥɶɧɨɟ
ɞɜɢɠɟɧɢɟ.
5. ɍɫɬɚɧɨɜɢɬɟ ɧɨɜɨɟ ɡɧɚɱɟɧɢɟ ɱɚɫɬɨɬɵ ɜɧɟɲɧɟɣ ɫɢɥɵ.
6. ɂɫɫɥɟɞɭɣɬɟ ɜɫɸ ɞɨɫɬɭɩɧɭɸ ɨɛɥɚɫɬɶ ɱɚɫɬɨɬ.
7. Ⱦɥɹ ɛɢɟɧɢɣ ɭɬɨɱɧɢɬɟ ɝɪɚɧɢɰɵ ɞɢɚɩɚɡɨɧɚ.
8. ɉɟɪɟɣɞɢɬɟ ɜ ɪɟɠɢɦ ɢɫɩɨɥɶɡɨɜɚɧɢɹ ɫɟɤɭɧɞɨɦɟɪɚ.
9. ɍɫɬɚɧɨɜɢɬɟ ɱɚɫɬɨɬɭ
ɜɧɟɲɧɟɣ ɫɢɥɵ, ɪɚɜɧɨɣ ɱɚɫɬɨɬɟ, ɫɨɨɬɜɟɬɫɬ-
ɜɭɸɳɟɣ ɧɚɱɚɥɭ ɞɢɚɩɚɡɨɧɚ ɛɢɟɧɢɣ.
10. ɉɨɫɬɪɨɣɬɟ ɝɪɚɮɢɤ ɤɨɨɪɞɢɧɚɬɵ ɬɟɥɚ ɢ ɢɡɦɟɪɶɬɟ ɜɪɟɦɹ ɧɟɫɤɨɥɶ-
ɤɢɯ ɤɨɥɟɛɚɧɢɣ.
11. ɉɨ ɝɪɚɮɢɤɭ ɢɡɦɟɪɶɬɟ ɧɚɢɛɨɥɶɲɭɸ ɢ ɧɚɢɦɟɧɶɲɭɸ ɚɦɩɥɢɬɭɞɭ
ɤɨɥɟɛɚɧɢɣ ɬɟɥɚ.

ɆɨɞɄ-05 ɋɥɨɠɟɧɢɟ ɤɨɥɟɛɚɧɢɣ. Ȼɢɟɧɢɹ
289
12. Ɉɩɪɟɞɟɥɢɬɟ ɱɚɫɬɨɬɭ ɫɨɛɫɬɜɟɧɧɵɯ ɤɨɥɟɛɚɧɢɣ ɢ ɚɦɩɥɢɬɭɞɵ
ɫɤɥɚɞɵɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ.
13. ȼɵɛɟɪɢɬɟ ɞɪɭɝɭɸ ɱɚɫɬɨɬɭ ɜɧɟɲɧɟɣ ɫɢɥɵ. ɉɨɜɬɨɪɢɬɟ ɨɩɵɬ, ɧɚ-
ɱɢɧɚɹ ɫ ɩɭɧɤɬɚ 10.
14. ɉɨɜɬɨɪɹɣɬɟ ɨɩɵɬ, ɩɨɤɚ ɧɟ ɞɨɫɬɢɝɧɟɬɟ ɤɨɧɰɚ ɞɢɚɩɚɡɨɧɚ ɛɢɟɧɢɣ.
15. ȼɵɱɢɫɥɢɬɟ ɫɪɟɞɧɟɟ ɡɧɚɱɟɧɢɟ ɱɚɫɬɨɬɵ ɫɨɛɫɬɜɟɧɧɵɯ ɤɨɥɟɛɚɧɢɣ
ɢ ɫɪɟɞɧɢɟ ɡɧɚɱɟɧɢɹ ɚɦɩɥɢɬɭɞ ɫɤɥɚɞɵɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ.
16. ȼɵɱɢɫɥɢɬɟ ɨɬɧɨɫɢɬɟɥɶɧɭɸ ɢ ɚɛɫɨɥɸɬɧɭɸ ɩɨɝɪɟɲɧɨɫɬɶ ɱɚɫɬɨ-
ɬɵ ɫɨɛɫɬɜɟɧɧɵɯ
ɤɨɥɟɛɚɧɢɣ ɢ ɚɦɩɥɢɬɭɞ.
17. ȼɵɱɢɫɥɢɬɟ ɬɟɨɪɟɬɢɱɟɫɤɨɟ ɡɧɚɱɟɧɢɟ ɫɨɛɫɬɜɟɧɧɨɣ ɱɚɫɬɨɬɵ.
18. ɋɞɟɥɚɣɬɟ ɜɵɜɨɞ.
4.2. ɉɨɞɪɨɛɧɨɟ ɨɩɢɫɚɧɢɟ ɯɨɞɚ ɪɚɛɨɬɵ
ɉɪɢ ɜɵɩɨɥɧɟɧɢɢ ɪɚɛɨɬɵ ɪɟɤɨɦɟɧɞɭɟɬɫɹ ɫɥɟɞɭɸɳɚɹ ɩɨɫɥɟɞɨɜɚ-
ɬɟɥɶɧɨɫɬɶ ɞɟɣɫɬɜɢɣ:
1. ɋ ɩɨɦɨɳɶɸ ɤɧɨɩɨɤ ɧɚ ɩɚɧɟɥɢ ɢɧɫɬɪɭɦɟɧɬɨɜ «Ɇɚɹɬɧɢɤ» ɜɵɛɟɪɢɬɟ ɦɚɹɬ-
ɧɢɤ (ɩɨ ɭɤɚɡɚɧɢɸ ɩɪɟɩɨɞɚɜɚɬɟɥɹ). ɉɨɞ ɤɧɨɩɤɚɦɢ ɚɜɬɨɦɚɬɢɱɟɫɤɢ ɭɤɚɡɵɜɚɸɬɫɹ ɡɧɚɱɟ-
ɧɢɹ ɤɨɷɮɮɢɰɢɟɧɬɚ ɠɟɫɬɤɨɫɬɢ ɩɪɭɠɢɧɵ ɢ ɦɚɫɫɚ ɬɟɥɚ. ɗɬɢ ɡɧɚɱɟɧɢɹ ɧɟɨɛɯɨɞɢɦɵ ɞɥɹ
ɜɵɱɢɫɥɟɧɢɹ ɬɟɨɪɟɬɢɱɟɫɤɢɯ ɡɧɚɱɟɧɢɣ ɱɚɫɬɨɬɵ ɫɨɛɫɬɜɟɧɧɵɯ (ɝɨɪɢɡɨɧɬɚɥɶɧɵɯ) ɤɨɥɟ-
ɛɚɧɢɣ.
ɗɌȺɉ 1. Ɉɩɪɟɞɟɥɟɧɢɟ ɞɢɚɩɚɡɨɧɚ ɛɢɟɧɢɣ
2. ɋ ɩɨɦɨɳɶɸ ɩɨɥɡɭɧɤɚ ɩɪɨɤɪɭɬɤɢ «ɑɚɫɬɨɬɚ» ɭɫɬɚɧɨɜɢɬɟ ɦɢɧɢɦɚɥɶɧɨɟ
ɡɧɚɱɟɧɢɟ ɱɚɫɬɨɬɵ ɜɧɟɲɧɟɣ ɫɢɥɵ. Ɍɨɱɧɨɟ ɡɧɚɱɟɧɢɟ ɱɚɫɬɨɬɵ ɭɤɚɡɵɜɚɟɬɫɹ ɧɚɞ ɩɨɥɡɭɧ-
ɤɨɦ ɩɪɨɤɪɭɬɤɚ ɜ ɜɢɞɟ: «ɑɚɫɬɨɬɚ ɜɧɟɲɧɟɣ ɫɢɥɵ (ɪɚɞ/ɫ): *.**».
3. ɉɨɫɬɪɨɣɬɟ ɝɪɚɮɢɤ ɤɨɨɪɞɢɧɚɬɵ ɬɟɥɚ.
Ⱦɥɹ ɷɬɨɝɨ ɧɚɠɦɢɬɟ ɤɧɨɩɤɭ «ɇɚɱɚɬɶ ɷɤɫɩɟɪɢɦɟɧɬ». ɇɚɱɧɟɬɫɹ ɞɜɢɠɟɧɢɟ ɦɚ-
ɹɬɧɢɤɚ. Ɉɞɧɨɜɪɟɦɟɧɧɨ ɫɬɪɨɹɬɫɹ ɝɪɚɮɢɤɢ ɡɚɜɢɫɢɦɨɫɬɢ ɤɨɨɪɞɢɧɚɬɵ ɬɟɥɚ ɨɬ ɜɪɟɦɟɧɢ
x = x(t) ɢ ɝɪɚɮɢɤɢ ɫɤɥɚɞɵɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ x
1
= x
1
(t) ɢ x
2
= x
2
(t). Ⱦɜɢɠɟɧɢɟ ɩɪɨɢɫɯɨ-
ɞɢɬ ɜ ɬɟɱɟɧɢɟ ɮɢɤɫɢɪɨɜɚɧɧɨɝɨ ɜɪɟɦɟɧɢ. Ʉɧɨɩɤɢ ɧɚ ɩɚɧɟɥɢ ɢɧɫɬɪɭɦɟɧɬɨɜ ɢ ɛɟɝɭɧɨɤ
ɩɪɨɤɪɭɬɤɢ «ɑɚɫɬɨɬɚ» ɫɬɚɧɭɬ ɧɟɞɨɫɬɭɩɧɵɦɢ. Ʉɨɝɞɚ ɜɪɟɦɹ ɷɤɫɩɟɪɢɦɟɧɬɚ ɡɚɤɨɧɱɢɬɫɹ,
ɦɚɹɬɧɢɤ ɚɜɬɨɦɚɬɢɱɟɫɤɢ ɨɫɬɚɧɨɜɢɬɫɹ.
ȿɫɥɢ ɜ ɩɪɨɰɟɫɫɟ ɷɤɫɩɟɪɢɦɟɧɬɚ ȼɵ ɜɫɩɨɦɧɢɥɢ, ɱɬɨ ɧɟɩɪɚɜɢɥɶɧɨ ɭɫɬɚɧɨɜɢɥɢ
ɤɚɤɭɸ-ɥɢɛɨ ɜɟɥɢɱɢɧɭ (ɜɵɛɪɚɥɢ ɦɚɹɬɧɢɤ ɢɥɢ ɱɚɫɬɨɬɭ ɜɧɟɲɧɟɣ ɫɢɥɵ), ɧɚɠɦɢɬɟ ɤɧɨɩ-
ɤɭ «Ɉɫɬɚɧɨɜɢɬɶ ɷɤɫɩɟɪɢɦɟɧɬ». Ɇɚɹɬɧɢɤ
ɨɫɬɚɧɨɜɹɬɫɹ. Ʉɧɨɩɤɢ ɧɚ ɩɚɧɟɥɢ ɢɧɫɬɪɭ-
ɦɟɧɬɨɜ ɢ ɛɟɝɭɧɨɤ ɩɪɨɤɪɭɬɤɢ «ɑɚɫɬɨɬɚ» ɫɬɚɧɭɬ ɞɨɫɬɭɩɧɵɦɢ. ɉɨɫɥɟ ɷɬɨɝɨ ɦɨɠɧɨ ɩɨ-
ɜɬɨɪɢɬɶ ɨɩɵɬ.
4. ɉɨ ɜɢɞɭ ɝɪɚɮɢɤɚ ɡɚɜɢɫɢɦɨɫɬɢ ɤɨɨɪɞɢɧɚɬɵ ɬɟɥɚ ɨɬ ɜɪɟɦɟɧɢ x = x(t) ɨɩɪɟɞɟ-
ɥɢɬɟ, ɤ ɤɚɤɨɦɭ ɬɢɩɭ ɨɬɧɨɫɢɬɫɹ ɞɚɧɧɨɟ ɤɨɥɟɛɚɬɟɥɶɧɨɟ ɞɜɢɠɟɧɢɟ.
5. ɋ ɩɨɦɨɳɶɸ ɩɨɥɡɭɧɤɚ ɩɪɨɤɪɭɬɤɢ «ɑɚɫɬɨɬɚ» ɭɫɬɚɧɨɜɢɬɟ ɧɨɜɨɟ ɡɧɚɱɟɧɢɟ
ɱɚɫɬɨɬɵ ɜɧɟɲɧɟɣ ɫɢɥɵ ɛɨɥɶɲɟ ɩɪɟɞɵɞɭɳɟɝɨ ɧɚ 0,5 ɪɚɞ/ɫ. ɉɨɜɬɨɪɢɬɟ ɨɩɵɬ, ɧɚɱɢɧɚɹ
ɫ ɩɭɧɤɬɚ 3.
6. ɂɫɫɥɟɞɭɣɬɟ ɜɫɸ ɞɨɫɬɭɩɧɭɸ ɨɛɥɚɫɬɶ ɱɚɫɬɨɬ (0 – 6 ɪɚɞ/ɫ) ɫ ɲɚɝɨɦ 0,5 ɪɚɞ/ɫ.
Ⱦɥɹ ɤɚɠɞɨɝɨ ɬɢɩɚ ɞɜɢɠɟɧɢɹ ɡɚɪɢɫɭɣɬɟ ɢɥɢ ɫɨɯɪɚɧɢɬɟ ɜ ɜɢɞɟ bmp-ɮɚɣɥɚ ɧɚɢɛɨɥɟɟ

Ʉɨɥɟɛɚɧɢɹ ɢ ɜɨɥɧɵ
290
ɯɚɪɚɤɬɟɪɧɵɣ ɝɪɚɮɢɤ ɡɚɜɢɫɢɦɨɫɬɢ ɤɨɨɪɞɢɧɚɬɵ ɬɟɥɚ ɨɬ ɜɪɟɦɟɧɢ x = x(t). ɑɬɨɛɵ ɫɨ-
ɯɪɚɧɢɬɶ ɝɪɚɮɢɤ, ɧɚɠɦɢɬɟ ɤɧɨɩɤɭ «ɋɨɯɪɚɧɢɬɶ ɝɪɚɮɢɤ».
ɊȿɁɍɅɖɌȺɌɕ ɂɋɋɅȿȾɈȼȺɇɂɃ ɁȺɉɂɒɂɌȿ ȼ ɌȺȻɅɂɐɍ 1.
7. Ⱦɥɹ ɛɢɟɧɢɣ ɭɬɨɱɧɢɬɟ ɝɪɚɧɢɰɵ ɞɢɚɩɚɡɨɧɚ ɫ ɬɨɱɧɨɫɬɶɸ 0,2 ɪɚɞ/ɫ.
Ʉɨɥɟɛɚɬɟɥɶɧɨɟ ɞɜɢɠɟɧɢɟ ɫɱɢɬɚɟɬɫɹ ɛɢɟɧɢɹɦɢ, ɟɫɥɢ ɡɚ ɨɞɢɧ ɩɟɪɢɨɞ ɢɡɦɟɧɟ-
ɧɢɹ ɚɦɩɥɢɬɭɞɵ ɬɟɥɨ ɫɨɜɟɪɲɚɟɬ ɦɧɨɝɨ (>5) ɤɨɥɟɛɚɧɢɣ.
ɂɡɦɟɧɹɣɬɟ ɱɚɫɬɨɬɭ ɜɧɟɲɧɟɣ ɫɢɥɵ ɫ ɲɚɝɨɦ 0,2 ɪɚɞ/ɫ ɞɨ ɬɟɯ ɩɨɪ, ɩɨɤɚ ɧɟ ɧɚɣ-
ɞɟɬɟ ɞɢɚɩɚɡɨɧ, ɜɧɭɬɪɢ ɤɨɬɨɪɨɝɨ ɡɚ ɨɞɢɧ ɩɟɪɢɨɞ ɢɡɦɟɧɟɧɢɹ ɚɦɩɥɢɬɭɞɵ ɬɟɥɨ ɛɭɞɟɬ
ɫɨɜɟɪɲɚɬɶ ɛɨɥɶɲɟ ɩɹɬɢ ɤɨɥɟɛɚɧɢɣ.
ɇɚɣɞɟɧɧɵɟ ɝɪɚɧɢɰɵ ɞɢɚɩɚɡɨɧɚ ɛɢɟɧɢɣ ɡɚɩɢɲɢɬɟ ɜ ɬɚɛɥɢɰɭ 1.
ɗɬɚɩ 2. Ɉɩɪɟɞɟɥɟɧɢɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤ ɫɤɥɚɞɵɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ.
8. ɉɟɪɟɣɞɢɬɟ ɜ ɪɟɠɢɦ ɢɫɩɨɥɶɡɨɜɚɧɢɹ ɫɟɤɭɧɞɨɦɟɪɚ.
Ⱦɥɹ ɷɬɨɝɨ ɧɚ ɫɟɤɭɧɞɨɦɟɪɟ ɭɫɬɚɧɨɜɢɬɟ ɩɟɪɟɤɥɸɱɚɬɟɥɶ
(ɮɥɚɠɨɤ) «ɂɫɩɨɥɶɡɨ-
ɜɚɬɶ ɫɟɤɭɧɞɨɦɟɪ». ɋɱɟɬɱɢɤ «Ʉɨɥɢɱɟɫɬɜɨ ɤɨɥɟɛɚɧɢɣ» ɢ ɩɨɥɟ «ȼɪɟɦɹ» ɫɟɤɭɧɞɨɦɟɪɚ
ɫɬɚɧɭɬ ɞɨɫɬɭɩɧɵɦɢ. Ɍɨɝɞɚ ɩɨɫɥɟ ɧɚɠɚɬɢɹ ɤɧɨɩɤɢ «ɇɚɱɚɬɶ ɷɤɫɩɟɪɢɦɟɧɬ» ɨɞɧɨɜɪɟ-
ɦɟɧɧɨ ɫ ɞɜɢɠɟɧɢɟɦ ɬɟɥɚ ɡɚɩɭɫɬɢɬɫɹ ɫɟɤɭɧɞɨɦɟɪ. ɋɟɤɭɧɞɨɦɟɪ ɨɫɬɚɧɨɜɢɬɫɹ ɚɜɬɨɦɚ-
ɬɢɱɟɫɤɢ ɩɨɫɥɟ ɬɨɝɨ, ɤɚɤ ɬɟɥɨ ɫɨɜɟɪɲɢɬ ɡɚɞɚɧɧɨɟ ɤɨɥɢɱɟɫɬɜɨ ɤɨɥɟɛɚɧɢɣ.
ɋ ɩɨɦɨɳɶɸ ɫɱɟɬɱɢɤɚ «Ʉɨɥɢɱɟɫɬɜɨ ɤɨɥɟɛɚɧɢɣ» ɭɫɬɚɧɨɜɢɬɟ ɱɢɫɥɨ ɩɨɥɧɵɯ
ɤɨɥɟɛɚɧɢɣ, ɜɪɟɦɹ
ɤɨɬɨɪɵɯ ɛɭɞɟɬ ɢɡɦɟɪɹɬɶ ɫɟɤɭɧɞɨɦɟɪ. Ɋɟɤɨɦɟɧɞɭɟɬɫɹ ɭɫɬɚɧɨɜɢɬɶ
ɦɚɤɫɢɦɚɥɶɧɨ ɜɨɡɦɨɠɧɨɟ ɤɨɥɢɱɟɫɬɜɨ ɤɨɥɟɛɚɧɢɣ.
9. ɍɫɬɚɧɨɜɢɬɟ ɱɚɫɬɨɬɭ ɜɧɟɲɧɟɣ ɫɢɥɵ, ɪɚɜɧɨɣ ɱɚɫɬɨɬɟ, ɫɨɨɬɜɟɬɫɬɜɭɸɳɟɣ ɧɚ-
ɱɚɥɭ ɞɢɚɩɚɡɨɧɚ ɛɢɟɧɢɣ.
10. ɉɨɫɬɪɨɣɬɟ ɝɪɚɮɢɤ ɤɨɨɪɞɢɧɚɬɵ ɬɟɥɚ ɢ ɢɡɦɟɪɶɬɟ ɜɪɟɦɹ ɧɟɫɤɨɥɶɤɢɯ ɤɨɥɟɛɚ-
ɧɢɣ.
Ⱦɥɹ ɷɬɨɝɨ ɧɚɠɦɢɬɟ ɤɧɨɩɤɭ «ɇɚɱɚɬɶ ɷɤɫɩɟɪɢɦɟɧɬ». ɇɚɱɧɟɬɫɹ ɞɜɢɠɟɧɢɟ ɦɚ-
ɹɬɧɢɤɚ. Ɉɞɧɨɜɪɟɦɟɧɧɨ ɜɤɥɸɱɢɬɫɹ ɫɟɤɭɧɞɨɦɟɪ, ɢ ɧɚɱɧɭɬ ɫɬɪɨɢɬɶɫɹ ɝɪɚɮɢɤɢ ɡɚɜɢɫɢ
-
ɦɨɫɬɢ ɤɨɨɪɞɢɧɚɬɵ ɬɟɥɚ ɨɬ ɜɪɟɦɟɧɢ x = x(t) ɢ ɝɪɚɮɢɤɢ ɫɤɥɚɞɵɜɚɟɦɵɯ ɤɨɥɟɛɚɧɢɣ
x
1
= x
1
(t) ɢ x
2
= x
2
(t). Ʉɧɨɩɤɢ ɧɚ ɩɚɧɟɥɢ ɢɧɫɬɪɭɦɟɧɬɨɜ ɢ ɛɟɝɭɧɨɤ ɩɪɨɤɪɭɬɤɢ «ɑɚɫɬɨɬɚ»
ɫɬɚɧɭɬ ɧɟɞɨɫɬɭɩɧɵɦɢ. Ⱦɜɢɠɟɧɢɟ ɩɪɨɢɫɯɨɞɢɬ ɜ ɬɟɱɟɧɢɟ ɮɢɤɫɢɪɨɜɚɧɧɨɝɨ ɜɪɟɦɟɧɢ.
ɋɟɤɭɧɞɨɦɟɪ ɨɫɬɚɧɨɜɢɬɫɹ ɚɜɬɨɦɚɬɢɱɟɫɤɢ ɩɨɫɥɟ ɬɨɝɨ, ɤɚɤ ɬɟɥɨ ɫɨɜɟɪɲɢɬ ɡɚɞɚɧɧɨɟ ɤɨ-
ɥɢɱɟɫɬɜɨ ɤɨɥɟɛɚɧɢɣ. Ʉɨɝɞɚ ɜɪɟɦɹ ɷɤɫɩɟɪɢɦɟɧɬɚ ɡɚɤɨɧɱɢɬɫɹ, ɦɚɹɬɧɢɤ ɚɜɬɨɦɚɬɢɱɟɫɤɢ
ɨɫɬɚɧɨɜɢɬɫɹ.
ȼɊȿɆə ɄɈɅȿȻȺɇɂɃ ɂ ɄɈɅɂɑȿɋɌȼɈ ɄɈɅȿȻȺɇɂɃ ɁȺɉɂɒɂɌȿ ȼ
ɌȺȻɅɂɐɍ 2.
11. ɉɨ ɝɪɚɮɢɤɭ ɢɡɦɟɪɶɬɟ ɧɚɢɛɨɥɶɲɭɸ ɢ ɧɚɢɦɟɧɶɲɭɸ
ɚɦɩɥɢɬɭɞɭ ɤɨɥɟɛɚɧɢɣ
ɬɟɥɚ.
ɋɨɜɦɟɫɬɢɬɟ ɢɡɦɟɪɢɬɟɥɶɧɭɸ ɥɢɧɢɸ ɩɨɥɡɭɧɤɚ ɩɪɨɤɪɭɬɤɢ «ɂɡɦɟɪɟɧɢɟ ɤɨɨɪɞɢ-
ɧɚɬɵ» ɫ ɧɚɛɨɥɶɲɢɦ ɩɨ ɚɦɩɥɢɬɭɞɟ ɦɚɤɫɢɦɭɦɨɦ ɝɪɚɮɢɤɚ ɡɚɜɢɫɢɦɨɫɬɢ ɤɨɨɪɞɢɧɚɬɵ
ɨɬ ɜɪɟɦɟɧɢ. Ⱦɥɹ ɛɨɥɟɟ ɬɨɱɧɨɝɨ ɫɨɜɦɟɳɟɧɢɹ ɢɫɩɨɥɶɡɭɣɬɟ ɫɤɪɨɥɥɢɧɝ ɦɵɲɢ. Ɂɧɚɱɟɧɢɟ
ɤɨɨɪɞɢɧɚɬɵ ɢɡɦɟɪɢɬɟɥɶɧɨɣ ɥɢɧɢɢ ɭɤɚɡɵɜɚɟɬɫɹ ɩɨɞ ɩɨɥɡɭɧɤɨɦ ɩɪɨɤɪɭɬɤɢ «ɂɡɦɟɪɟ-
ɧɢɟ ɤɨɨɪɞɢɧɚɬɵ» ɜ ɜɢɞɟ «Ʉɨɨɪɞɢɧɚɬɚ x(ɫɦ): *.**».
ɉɨɜɬɨɪɢɬɟ ɢɡɦɟɪɟɧɢɹ ɞɥɹ ɧɚɢɦɟɧɶɲɟɝɨ ɩɨ
ɚɦɩɥɢɬɭɞɟ ɦɚɤɫɢɦɭɦɚ ɝɪɚɮɢɤɚ.
ɁɇȺɑȿɇɂə ɇȺɂȻɈɅɖɒȿɃ ɂ ɇȺɂɆȿɇɖɒȿɃ ȺɆɉɅɂɌɍȾ ɁȺɉɂɒɂɌȿ
ȼ ɌȺȻɅɂɐɍ 2.
