Маршалл Дж.Ф., Бансал В.К. Финансовая инженерия Полное руководство по финансовым нововведениям

Подождите немного. Документ загружается.

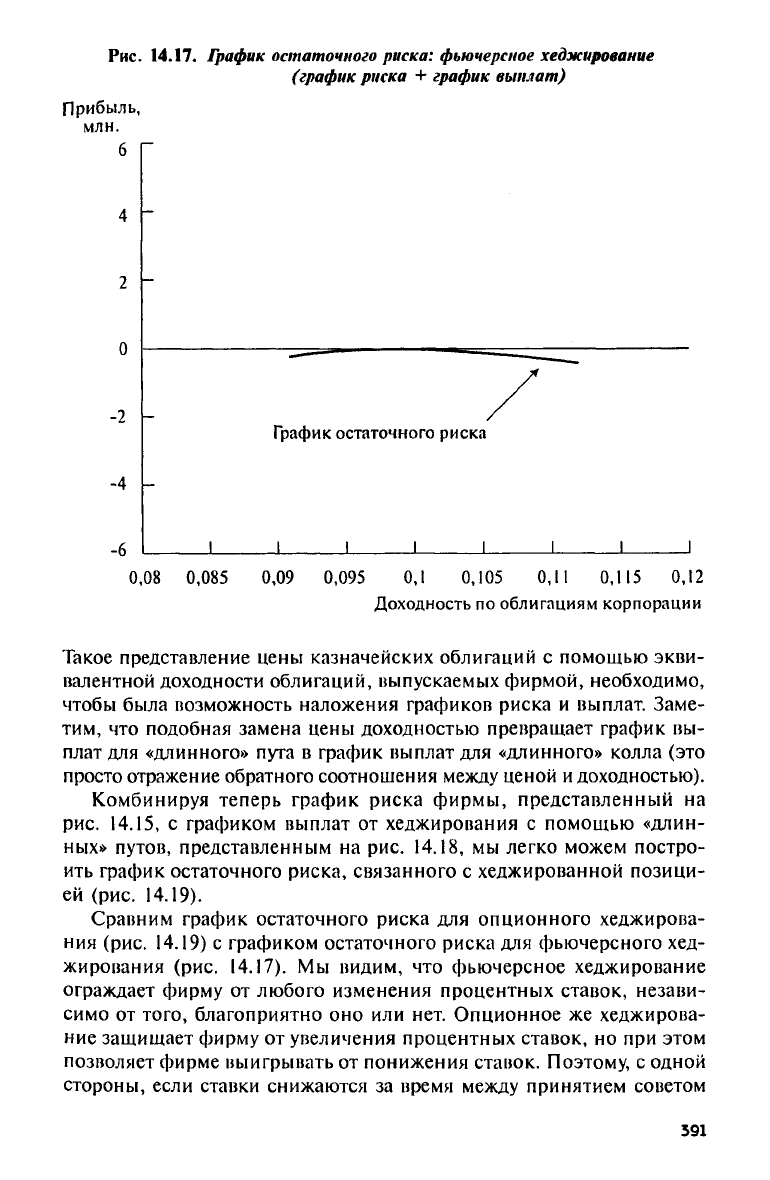
Рис.

14.17.

График остаточного риска: фьючерсное хеджирование

(график риска

график выплат)

Такое представление цены казначейских облигаций

помощью экви-

валентной доходности облигаций, выпускаемых фирмой, необходимо,

чтобы была возможность наложения графиков риска

выплат. Заме-

тим,

что

подобная замена цены доходностью превращает график

вы-

плат

для

«длинного» пута

график выплат

для

«длинного» колла

(это

просто отражение обратного соотношения между ценой

доходностью).

Комбинируя теперь график риска фирмы, представленный

на

рис.

14.15, с

графиком выплат

от

хеджирования

помощью «длин-

ных» путов, представленным

на рис. 14.18, мы

легко можем постро-

ить график остаточного риска, связанного

хеджированной позици-

ей

(рис. 14.19).

Сравним график остаточного риска

для

опционного хеджирова-

ния

(рис. 14.19) с

графиком остаточного риска

для

фьючерсного хед-

жирования

(рис. 14.17). Мы

видим,

что

фьючерсное хеджирование

ограждает фирму

от

любого изменения процентных ставок, незави-

симо

от

того, благоприятно

оно или нет.

Опционное

же

хеджирова-

ние защищает фирму

от

увеличения процентных ставок,

но при

этом

позволяет фирме выигрывать

от

понижения ставок. Поэтому,

одной

стороны, если ставки снижаются

за

время между принятием советом

391

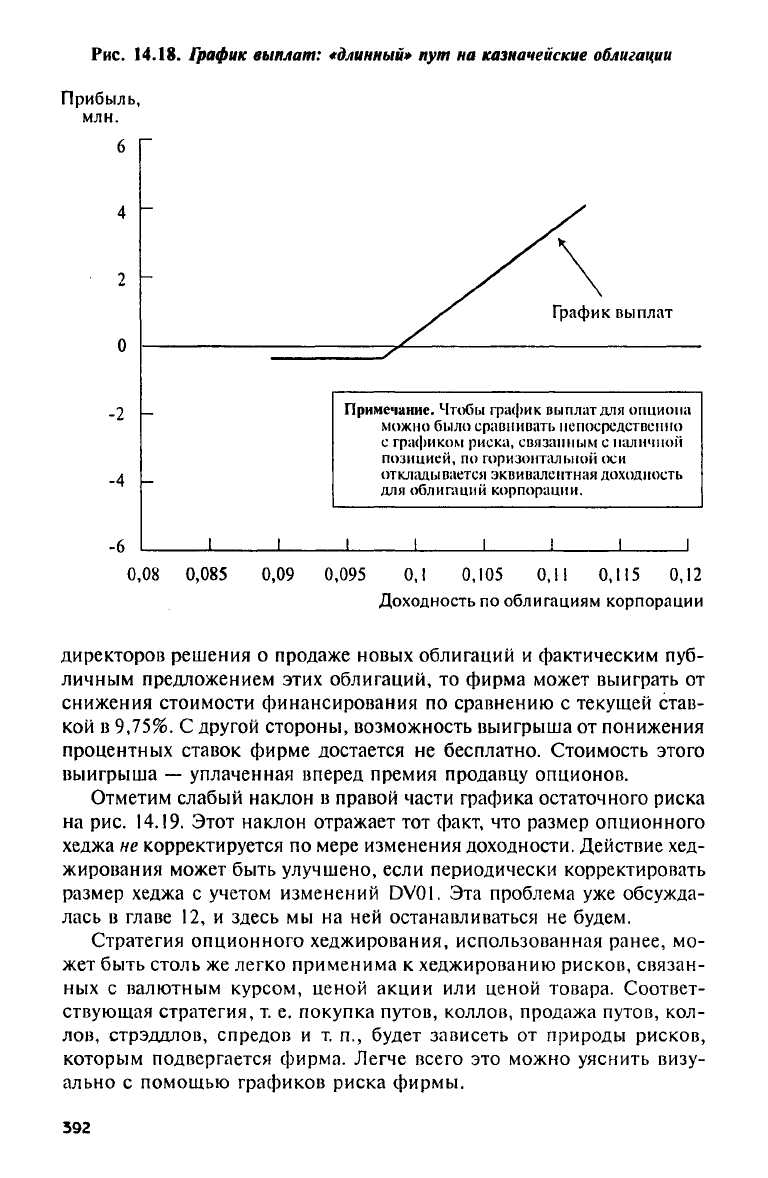
Рис.

14.18.

График выплат:

«длинный»

пут на

казначейские облигации

директоров решения

продаже новых облигаций

фактическим пуб-

личным предложением этих облигаций,

то

фирма может выиграть

от

снижения стоимости финансирования

по

сравнению

текущей став-

кой

в 9,75%. С

другой стороны, возможность выигрыша

от

понижения

процентных ставок фирме достается

не

бесплатно. Стоимость этого

выигрыша

—

уплаченная вперед премия продавцу опционов.

Отметим слабый наклон

правой части графика остаточного риска

на

рис. 14.19.

Этот наклон отражает

тот

факт,

что

размер опционного

хеджа

не

корректируется

по

мере изменения доходности. Действие хед-

жирования может быть улучшено, если периодически корректировать

размер хеджа

учетом изменений

DV01. Эта

проблема

уже

обсужда-

лась

главе

12, и

здесь

мы на ней

останавливаться

не

будем.

Стратегия опционного хеджирования, использованная ранее,

мо-

жет быть столь

же

легко применима

хеджированию рисков, связан-

ных

валютным курсом, ценой акции

или

ценой товара. Соответ-

ствующая стратегия,

т. е.

покупка путов, коллов, продажа путов,

кол-

лов,

стрэддлов, спредов

и т. п.,

будет зависеть

от

природы рисков,

которым подвергается фирма. Легче всего

это

можно уяснить визу-

ально

помощью графиков риска фирмы.

392

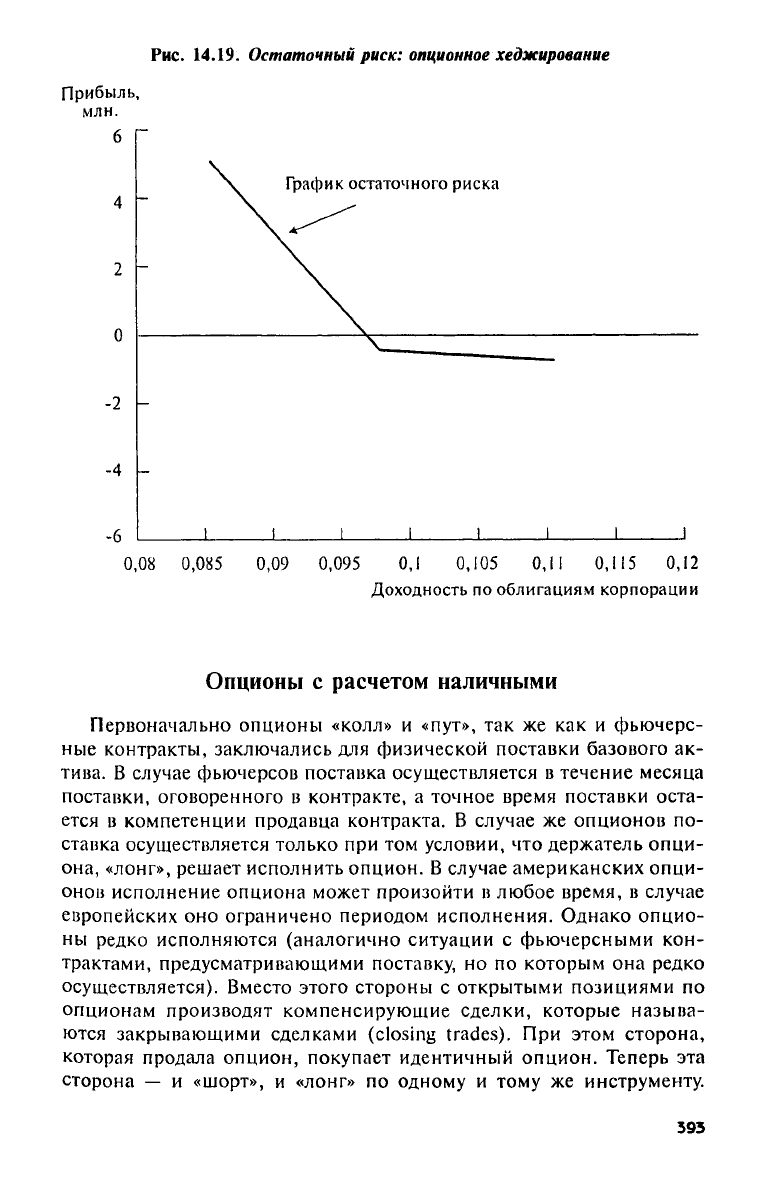
Рис.

14.19.

Остаточный риск:

опционное

хеджирование

Опционы

расчетом наличными

Первоначально опционы «колл»

«пут»,

так же как и

фьючерс-

ные контракты, заключались

для

физической поставки базового

ак-

тива.

случае фьючерсов поставка осуществляется

течение месяца

поставки, оговоренного

контракте,

точное время поставки оста-

ется

компетенции продавца контракта.

случае

же

опционов

по-

ставка осуществляется только

при том

условии,

что

держатель опци-

она, «лонг», решает исполнить опцион.

случае американских опци-

онов исполнение опциона может произойти

любое время,

случае

европейских

оно

ограничено периодом исполнения. Однако опцио-

ны редко исполняются (аналогично ситуации

фьючерсными кон-

трактами, предусматривающими поставку,

но по

которым

она

редко

осуществляется). Вместо этого стороны

открытыми позициями

по

опционам производят компенсирующие сделки, которые называ-

ются закрывающими сделками

(closing

trades). При

этом сторона,

которая продала опцион, покупает идентичный опцион. Теперь

эта

сторона

— и

«шорт»,

«лонг»

по

одному

тому

же

инструменту.

393

Клиринговая палата затем вычеркивает один «лонг»

один «шорт»,

тем самым закрывая позицию члена биржи, участвующего

торгах

за

свой счет.

Вскоре после появления расчетов наличными

(cash

settlement) по

фьючерсным контрактам

на

основе фондовых индексов фьючерсные

биржи убедили

CFTC

разрешить торговлю опционами

на

фьючерсы,

названные фьючерсными опционами

(futures options), на

экспери-

ментальной основе. Эксперимент оказался удачным,

позже торго-

вать

ими

стали постоянно. Фьючерсными опционами сейчас торгуют

на большинстве фьючерсных бирж. Цель продажи опциона

на

фьючерсы

—

разрешить продавцу

(в

случае колла)

или

покупателю

(в случае пута) опциона поставить стандартизованную единицу базо-

вого актива (фьючерсный контракт), если «лонг» решает исполнить

опцион.

появлением опционов

на

индексные фьючерсы

мы

полу-

чили опцион, который, будучи исполненным, имел

результате

по-

ставку фьючерсного контракта,

по

которому потом производился рас-

чет наличными.

От

такого опциона было

уже

недалеко

до

опциона

на

фондовый индекс,

по

которому рассчитывались наличными

по

исте-

чении срока опциона. Такие опционы

не

требуют

от

того,

кто

имеет

«длинную» позицию, явного решения исполнить опцион. Вместо этого

продавец опциона платит

его

держателю сумму, эквивалентную раз-

меру выигрыша

или

нулю

(что

окажется больше)

момент истечения

срока.

Опционы

на

фондовые индексы

расчетом наличными быстро

вытеснили опционы

на

индексные фьючерсы.

Они

также проложили

путь другим типам опционов

расчетом наличными, включая про-

центные кэпы

процентные флоры,

которыми

мы.

познакомимся

в следующей главе.

Резюме

Опционы

— это

контракты, которые гарантируют своему покупате-

лю право,

но не

обязательство, что-либо предпринять. Чаще всего

это право купить

или

продать некоторое количество единиц некото-

рого базового актива.

случае расчетов наличными

это

право озна-

чает право получения наличных выплат. Опционы имеют ограничен-

ный срок действия. Если опцион

не

исполняется

концу своей «жиз-

ни»,

то его

срок истекает

и он

становится бесполезным. Опционы,

которые могут быть исполнены

любое время, называются амери-

канскими,

а те,

которые можно исполнить лишь

течение очень огра-

ниченного периода,

—

европейскими.

Традиционные формы опционов

— это

коллы

путы. Опционы

«колл» гарантируют

их

держателям право покупки некоторого коли-

чества единиц базового актива

по

цене исполнения, тогда

как

опци-

394

оны «пут» гарантируют

их

владельцам право продать некоторое

ко-

личество единиц базового актива

по

цене исполнения.

За это

право,

которое предоставляет опцион,

его

покупатель платит вперед про-

давцу опциона некоторую сумму, называемую премией опциона.

Опционы привлекательны

как

инструменты спекуляции, потому

что

они

предоставляют спекулянту значительный финансовый рычаг,

строго ограничивая

при

этом односторонний риск.

Они

также при-

влекательны

и для

хеджеров, потому

что

обеспечивают способ защи-

ты

от

неблагоприятных изменений

цен и в то же

время оставляют

возможность получить прибыль

при

благоприятных изменениях

цен.

Графики выплат, соответствующие опционам, немного сложнее,

чем

аналогичные графики

для

фьючерсных

форвардных контрактов.

Кроме того,

эти

инструменты можно комбинировать многими спо-

собами, создавая

при

этом богатейший ассортимент уникальных при-

быльных конструкций,

и это

является причиной значительного

ин-

тереса

опционам финансовых инженеров.

Модели оценивания опционов слишком сложны. Большинство

этих моделей разрабатывались

как

варианты известной модели

Блэка-Шоулза. Даже

те

модели, которые

не

анонсировались

как мо-

дификации модели Блэка-Шоулза, очень напоминают

эту

модель.

Стоимость опциона складывается

из

двух составляющих. Первая

на-

зывается внутренней стоимостью

может быть определена

помощью

функции максимума

(max).

Другими словами, внутренняя стоимость

опциона

— это

выигрыш опциона

или

нуль,

зависимости оттого,

что

больше. Вторая составляющая стоимости опциона

— это

временная

стоимость. Временная стоимость представляет собой потенциал уве-

личения внутренней стоимости

до

истечения срока опциона.

Если более ранние опционы предполагали физическую поставку

базового актива,

то

многие опционы, появившиеся

последние

го-

ды,

уже

специально разрабатывались

так,

чтобы расчет

по ним

про-

изводился наличными. Расчеты наличными

—

очень привлекатель-

ный момент, который,

тому

же,

значительно сокращает издержки,

связанные

исполнением опциона. Расчеты наличными также про-

ложили путь многопериодным опционам.

Примечания

'Читатель, интересующийся математическим аппаратом, использующим-

ся

моделях оценивания опционов, должен ознакомиться

со

следующими

работами:

Marshal! (1989), Ritchken (1987), Сох and Rubinstein (1985) и

Jarrow

and Rudd (1983).

Читатель, интересующийся математикой стохастических рас-

четов, может ознакомиться

с Shimko (1991) и Ritchken (1987).

Пакет Α-Pack, описанный

примечаниях

главе

— довольно типич-

ный пример недорогого программного обеспечения

для

микрокомпьютера,

которое использует модель оценивания опциона Блэка-Шоулза.

395

Для более подробного изучения этих моделей оценивания опционов,

их

развития

эмпирической проверки

см.

Ссылки

рекомендуемую литерату-

ру

этой главе.

Для более детального ознакомления

каждой

из

этих стратегий,

также

с формулами

для

расчетов соответствующих графиков выплат

см. Marshall

(1989),

главы

17-20.

Ссылки

рекомендуемая литература

Ball,

С. and W. Torous. «Оп

Jumps

in Common Stock

Prices

and Their Impact on

Call

Option Pricings

Journal

Finance,

40 (1985), pp. 155-173.

Ball,

C. and W. Torous.

«Futures

Options and the

Volatility

Futures

Prices*,

Journal

Finance,

41 (1986), pp. 857-870.

Black,

«The

Pricing of Commodity Contracts*,

Journal

Financial

Economics,

4 (1976), pp. 167-179.

Black,

F. and M.

Scholes.

«The

Pricing of Options and Corporate

Liabilities*,

Journal

Political

Economy

(May/June 1973), pp. 637—659.

Bodurtha, R. and N.

Gonedes.

«Tests

of the American Option Pricing

Model

oil

the Foreign

Currence

Options Market*,

Journal

Financial

and

Quantitative

Analysis,

22 (1987), pp. 153-167.

Borensztein, E. and M. Dooley.

«Options

on Foreign

Exchange

and

Exchange

Rate

Expectations*,

International

Monetary

Fund

Staff

Papers,

34 (1987), pp. 643—

680.

Cox, J.C. and M. Rubinstein.

Options

Markets, Englewood

Cliffs,

NJ: Prentice'.

Hall,

1985.

Jarrow, R.A. and A. Rudd.

Option

Pricing,

Homewood, IL:

Irwin,

1983.

Marshall,

J.F.

Futures

and

Option

Contracting:

Theory

and

Practice,

Cincinnati, OH:

South-Westem, 1989.

Merton,

«Option

Pricing When Underlying Stock

Returns

are Discontinuous*,

Journal

Financial

Economics,

3 (1976), pp. 125—144.

Ogden, J. and

Tucker.

«Empirical

Tests

of the

Efficiency

of the Currency

Futures

Options Market*,

Journal

Futures

Markets, 7 (1987), pp. 695-703.

Ritchey, R.

«Call

Option Valuation for Discrete Normal Mixtures*,

Journal

Fi-

nancial

Research,

13 (1990), pp. 285-296.

Ritchken, P.

Options:

Theory,

Strategy,

and

Applications,

Glenview,

IL:

Scott,

Fores-

man, 1987.

Shastri, K. and K. Wethyavivurn.

«The

Valuation of Currency Options for Alterna-

tive

Stochastic

Processes*,

Journal

Financial

Research,

10 (1987), pp. 283—

293.

Shimko, D.C.

Continuous-Time

Asset

Valuation

Finance:

Primer,

Miami,

FL:

Kolb

Publishing, 1991.

Глава 15

Многопериодные опционы:

кэпЫу

флоры, коллары, кэпционы,

свопционы и сложные опционы

Обзор

Инструменты, которые мы будем обсуждать в этой главе, подобны

рассмотренным в главе 14, потому что все они — опционы. Однако

они отличаются от рассмотренных в главе 14 тем, что являются либо

многопериодными опционами, либо опционами на многопериодные

инструменты. В частности, мы изучим многопериодные процентные

опционы, включая процентные кэпы, процентные флоры и процент-

ные коллары. Мы также обсудим опционы на процентные кэпы, на-

зываемые кэпционами, и опционы на свопы, называемые свопцио-

нами. Наконец, мы обсудим сложные опционы.

Многопериодные опционы — действительно новый продукт фи-

нансовой инженерии. Когда мы писали год назад первый вариант

этой главы, следующие два предложения звучали так: «Очень похо-

же,

что идеи, на которых основаны разработанные в последние годы

многопериодные процентные опционы, можно применить и в других

областях. Например, можно с уверенностью сказать, что разработка

многопериодных валютных опционов и многопериодных товарных

опционов — это только вопрос времени». За время, прошедшее по-

сле написания этих строк, многопериодные валютные опционы ста-

ли применяться повсеместно, а многопериодные товарные опционы

ждут своего часа. Так как мы не будем уделять внимания этим двум

видам опционов в настоящей главе, заметим лишь, что их структура

аналогична структуре многопериодных процентных опционов, кото-

рые мы будем рассматривать.

Многопериодные опционы особенно интересны, так как они лег-

ко комбинируются с другими инструментами (такими, как свопы) с

целью разработки интересных графиков выплат и получения специа-

397

лизированных решений финансовых проблем. Чуть позже

мы

рас-

смотрим

этой главе несколько способов комбинирования опционов

со свопами.

Как и в

предыдущей главе,

мы не

будем обсуждать формулы

для оценивания опционов. Читателя, интересующегося этой проблемой,

мы отошлем

ссылкам

настоящей

предыдущей главам

Процентные кэпы (кэпы)

С точки зрения хеджера, опционы,

по

которым производятся

расчеты наличными (такие,

как

опционы

на

фондовые индексы), огра-

ничены

по

своей применимости теми случаями, когда хеджер озабо-

чен флуктуациями

цен на

достаточно коротком временном отрезке.

Будем говорить

об

этом отрезке времени

как об

одном периоде. Дру-

гими словами, будем считать,

что

этому периоду соответствует одно-

кратный расчет наличными, который завершит опцион

день исте-

чения срока. Предположим далее,

что

фирма подвергается риску,

который может охватывать много таких периодов (один

за

другим).

Такая ситуация может,

примеру, возникнуть, если фирма выплачи-

вает

по

своим долгосрочным долговым обязательствам полугодовую

плавающую ставку процента

озабочена повышением процентных

ставок.

Теоретически такой риск можно хеджировать, «связывая» вместе

набор однопериодных процентных опционов, каждый

из

которых

будет исполнен ровно через шесть месяцев.

Но это не

слишком прак-

тично

по

двум причинам. Во-первых,

это

предполагает,

что в

течение

месяца поставки каждый контракт будет достаточно ликвидным

для

того,

чтобы заключить следующий контракт

без

существенных

из-

держек неликвидности. Во-вторых,

это

означает,

что

уже сегодня дол-

жна быть уверенность

возможности заключить серию контрактов

необходимыми месяцами поставки

весьма отдаленном будущем.

Обычно

оба эти

предположения

не

сбываются.

На

практике только

первые один-два месяца контракты бывают ликвидными (если

они

вообще ликвидны),

обычные коллы

путы почти никогда

не

про-

даются

датой исполнения большей,

чем на год

вперед, хотя долго-

срочными коллами

путами недавно

начали торговать

на

биржах.

Решение поставленной ранее задачи можно получить

помощью

специальных опционов, которыми торгуют

на

внебиржевых дилер-

ских рынках.

Эти

опционы называются процентными кэпами

(interest

rate caps) и

процентными флорами

(interest rate

floors).

Мы

начнем

процентных кэпов, которые часто называют просто кэпами

(caps).

Покупатель кэпа платит

его

владельцу каждый

раз,

когда контракт-

ная ставка-ориентир

(reference rate)

превышает ставку «потолок»

(ceiling

rate)

контракта

на

дату расчета. Базируясь

на

структуре кэпа,

398

можно осуществить многопериодное хеджирование против роста про-

центных ставок. Важно отметить,

что

хотя кэпы

являются много-

периодными опционами, однако премии полностью выплачиваются

вперед.

Большинство дилеров

по

кэпам,

так же как и

дилеров

по

свопам,

—

это коммерческие

инвестиционные банки. Дилеры

продают,

покупают кэпы, имея прибыль

на

спреде между ценами «бид»

«аск».

Премия

по

кэпу выражается

процентах

от

условной основной сум-

мы,

на

которую продается

кэп.

Например, пусть дилер работает

3-летними кэпами

по

ставке

6-М

LIBOR

ценой исполнения (ставка

«кэп»

— cap

rate)

в 8%.

Дилер

мог бы

купить

кэп за 1,28% и

продать

за

1,34%, т.е.

дилер продаст

кэп с

премией

в 1,34% и

купит

кэп с

премией

в 1,28%.

Разность между ценами «бид»

«аск»

0,06% (6 ба-

зисных пунктов)

— это и

есть дилерский бид-аск спред.

Прежде чем обсуждать вопросы, связанные

применением кэпов,

давайте более внимательно изучим структуру кэпа

процедуру рас-

четов. Дилер

его клиент заключают соглашение,

котором они опре-

деляют продолжительность кэпа (например,

два

года

или

пять лет),

ставку-ориентир (такую,

как

3-месячную ставку LIBOR, 6-месячную

ставку LIBOR

или

ставку 3-месячного казначейского векселя),

так-

же контрактную

(contract)

ставку

—

ставку «потолок», которая слу-

жит ценой исполнения кэпа

иногда называется ставкой «кэп», услов-

ную основную сумму

(notional

principal)

кэпа

даты расчета

(settlement

dates).

Продолжительность кэпа называется

его

сроком

(tenor).

При

наступлении даты первого расчета продавец кэпа платит

его

держа-

телю сумму, определяемую уравнением 15.1.

Эта

сумма пересчитыва-

ется

на

дату калькуляции, предшествующую каждой дате расчета.

Если дилер

—

продавец кэпа,

то он

платит клиенту некоторую над-

лежащую сумму. Если дилер — держатель кэпа,

то

клиент платит

ему

должную сумму.

(15.1)

где

D —

фиктивная переменная, принимающая значение

+1,

если

дилер продает

кэп, и

-1, если дилер покупает

кэп; max —

функция

максимума, описанная

главе

14; NP —

условная основная сумма;

LPP

— длина расчетного периода. Значение

LPP

зависит

от

выбора

ставки-ориентира

частоты выплат. Например, LIBOR котируется

на

основе «фактического количества дней

из

360». Поэтому

LPP для

6-месячной ставки LIBOR — это обычно число между

181/360

184/360.

Если расчет

по

формуле

15.1

дает положительное число

(что

может

случиться только

в том

случае, если дилер

—

продавец кэпа),

то ди-

399

лер платит клиенту. Если расчетная величина отрицательная (если

дилер — покупатель кэпа), то клиент платит дилеру. Если в результате

расчета получается нуль, то никто ничего не платит.

Уравнение 15.1 можно использовать для построения графика

выплат для кэпа. График выплат построен для единственной даты

расчета, но он выглядит так же для каждой даты расчета, охваты-

ваемой кэпом. График выплат для покупателя кэпа представлен на

рис.

15.1.

Рис. 15.1. График выплат для покупателя кэпа (на расчетный период)

Заметим, что график выплат для кэпа выглядит так же, как график

выплат для «длинного» колла, обсуждавшегося в главе 14. Но это сход-

ство обманчиво. Для опциона «колл» по горизонтальной оси обычно от-

кладывалась цена, а не ставка процента. Если ставку на графике кэпа по

горизонтальной оси заменить ценой, то график в действительности вы-

глядит также, как график «длинного» пута на долговой инструмент. При-

чина все та же — ставки (доходности) и цены связаны обратной зависи-

мостью. Приведенные рассуждения позволяют утверждать, что кэпы

аналогичны опционам «пут» для целей хеджирования и могут быть точ-

но описаны как многопериодные путы. (Тем не менее из -за формы гра-

фика выплат на них часто ссылаются как на многопериодные коллы.)

Так как кэп — многопериодный опцион, а премия за него выплачи-

вается вперед в виде одной общей суммы, график выплат, чтобы

отражать реалии, должен учитывать амортизацию премии. Пусть, на-

пример, 4-летний кэп с полугодовыми расчетными периодами может

быть продан за 1,85% от условной основной суммы. Тогда премию нуж-

но пропорционально изменить с помощью стандартной формулы амор-

тизации. Для этой цели мы используем уравнение 15.2.

400