Маршалл Дж.Ф., Бансал В.К. Финансовая инженерия Полное руководство по финансовым нововведениям

Подождите немного. Документ загружается.

Товарные свопы

Последний

вид

свопа,

на

котором

мы

остановимся,

—

товарный

своп.

товарном свопе

(commodity

swap)

первый контрагент произ-

водит периодические выплаты второму

по

фиксированной цене

за

единицу некоторого товара

при

заданном

его

количестве. Второй

контрагент платит первому

по

плавающей цене

за

единицу товара

(обычно

это

средняя цена, основанная

на

периодических наблюде-

ниях спотовой цены) тоже

при

заданном количестве товара. Товары

могут быть одни

и те же

(обычный случай)

или

различные. Если

они

одни

и те же, то

никакого обмена условными суммами (количества-

ми)

не

требуется. Если товары различные,

то

обмены условными сум-

мами могли

бы

потребоваться,

но, как

правило, никаких обменов

условными суммами

не

происходит

— все

сделки

по

актуалам произ-

водятся

на

наличных рынках.

Рассмотрим простой случай, когда производитель сырой нефти

(контрагент

А)

хочет зафиксировать

на

пять

лет

цену, которую

он

получает

за

свой товар, причем месячная производительность состав-

ляет

8000

баррелей.

В то же

время контрагент

Z?,

который занимается

очисткой нефти

производством химических продуктов, хочет

за-

фиксировать

на

пять

лет

цену, которую

он

платит

за

нефть,

— его

месячная потребность

нефти составляет

ООО баррелей. Чтобы

до-

стичь желаемых результатов, контрагенты заключают контракты

«своп» (каждый свой)

со

своповым дилером,

но

свои сделки

акту-

алах осуществляют

на

наличных рынках.

К моменту заключения контрактов «своп» цена неочищенной

нефти

на

спотовом рынке составляла

15,25 дол. за

баррель. Контр-

агент

соглашается производить ежемесячные платежи дилеру

по

цене

15,30 дол. за

баррель,

своповый дилер соглашается платить

контрагенту

среднесуточную цену нефти

за

предыдущий месяц.

то же

самое время контрагент

соглашается платить своповому

дилеру среднесуточную цену «спот»

за

предыдущий месяц

обмен

на

выплаты

от

дилера

по

цене

15,20 дол. за

баррель.

Как

следует

из

рис.

13.11, такие платежи фиксируют цену неочищенной нефти

для

обоих партнеров — производящего сырую нефть

очищающего нефть.

Разные условные количества нефти

этих двух свопах затрагива-

ют интересный вопрос. Если

бы

контрагенты

А и В

попытались

за-

ключить своп напрямую между собой,

то им бы это не

удалось из-за

различных требований сторон

по

объемам нефти. Однако присутствие

свопового дилера делает

оба

свопа жизнеспособными. Своповый

ди-

лер может компенсировать риск

от

несоответствия объемов, заклю-

чив третий своп

на

поставку

4000

баррелей

по

фиксированной цене.

до тех пор,

пока подходящий контрагент

не

будет найден, свопо-

вый дилер может хеджировать

помощью фьючерсов.

361

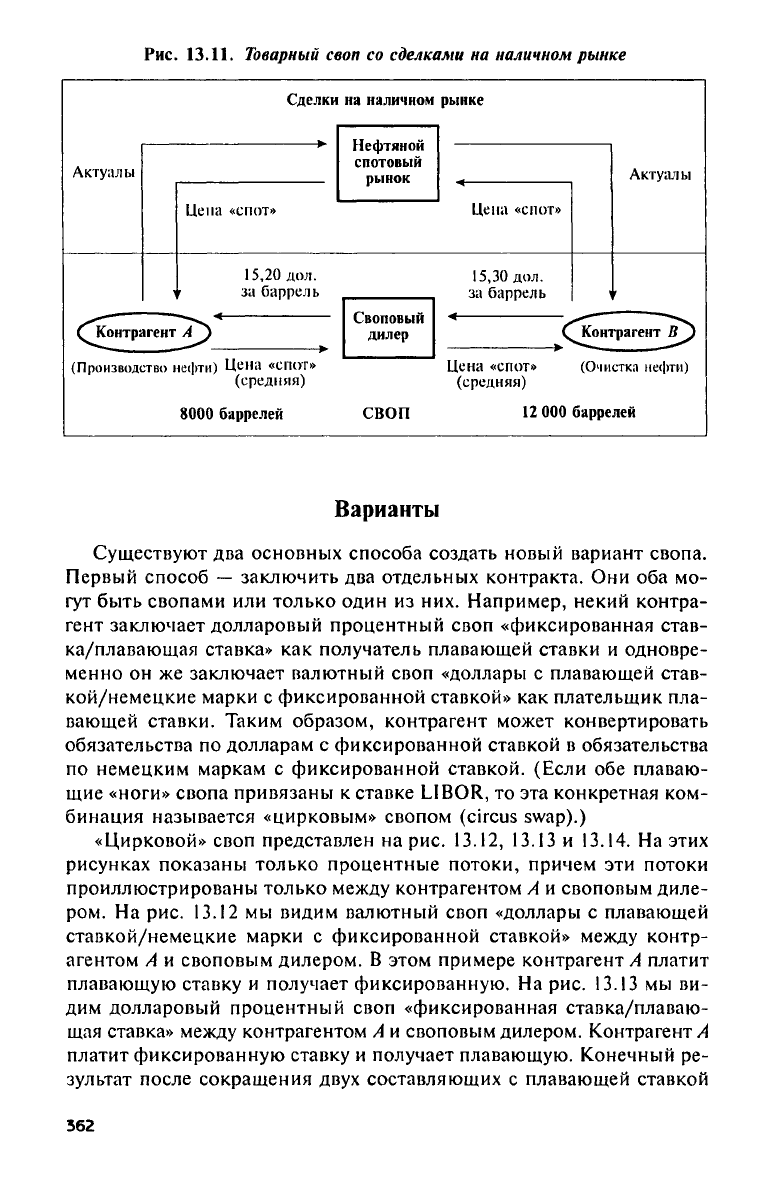
Рис.

13.11.

Товарный своп

со

сделками

на

наличном рынке

Варианты

Существуют

два

основных способа создать новый вариант свопа.

Первый способ

—

заключить

два

отдельных контракта.

Они оба мо-

гут быть свопами

или

только один

из них.

Например, некий контра-

гент заключает долларовый процентный своп «фиксированная став-

ка/плавающая ставка»

как

получатель плавающей ставки

одновре-

менно

он же

заключает валютный своп «доллары

плавающей став-

кой/немецкие марки

фиксированной ставкой»

как

плательщик пла-

вающей ставки. Таким образом, контрагент может конвертировать

обязательства

по

долларам

фиксированной ставкой

обязательства

по немецким маркам

фиксированной ставкой. (Если

обе

плаваю-

щие «ноги» свопа привязаны

ставке LIBOR,

то эта

конкретная ком-

бинация называется «цирковым» свопом

(circus swap).)

«Цирковой» своп представлен

на рис. 13.12, 13.13 и 13.14. На

этих

рисунках показаны только процентные потоки, причем

эти

потоки

проиллюстрированы только между контрагентом

А и

своповым диле-

ром.

На рис. 13.12 мы

видим валютный своп «доллары

плавающей

ставкой/немецкие марки

фиксированной ставкой» между контр-

агентом

А и

своповым дилером.

этом примере контрагент

платит

плавающую ставку

получает фиксированную.

На рис. 13.13 мы ви-

дим долларовый процентный своп «фиксированная ставка/плаваю-

щая ставка» между контрагентом

А и

своповым дилером. Контрагент

платит фиксированную ставку

получает плавающую. Конечный

ре-

зультат после сокращения двух составляющих

плавающей ставкой

362

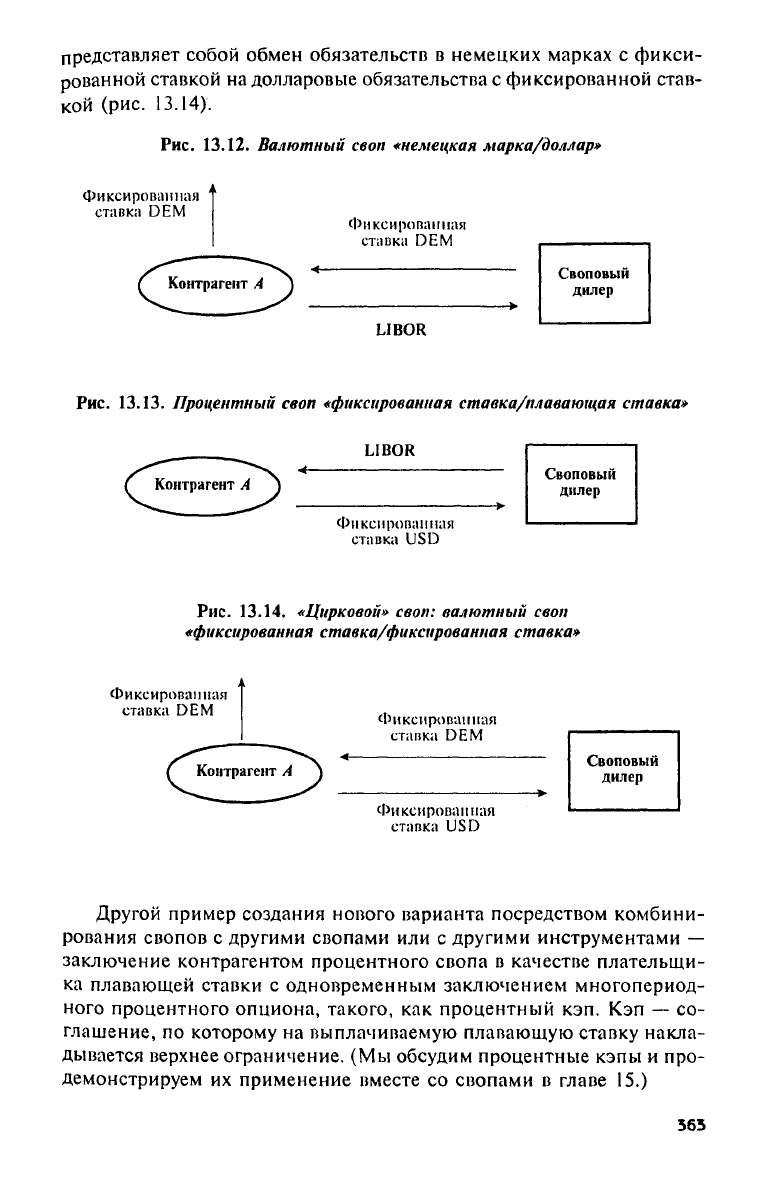
представляет собой обмен обязательств

немецких марках

фикси-

рованной ставкой

на

долларовые обязательства

фиксированной став-

кой

(рис.

13.14).

Рис.

13.12.

Валютный своп «немецкая марка/доллар»

Рис.

13.13.

Процентный своп «фиксированная ставка/плавающая ставка»

Рис.

13.14.

«Цирковой» своп: валютный своп

«фиксированная ставка/фиксированная ставка»

Другой пример создания нового варианта посредством комбини-

рования свопов

другими свопами

или с

другими инструментами

—

заключение контрагентом процентного свопа

качестве плательщи-

ка плавающей ставки

одновременным заключением многопериод-

ного процентного опциона, такого,

как

процентный

кэп. Кэп — со-

глашение,

по

которому

на

выплачиваемую плавающую ставку накла-

дывается верхнее ограничение.

(Мы

обсудим процентные кэпы

про-

демонстрируем

их

применение вместе

со

свопами

главе

15.)

363

Еще один способ создать новый вариант свопа

—

изменить усло-

вия самого свопа. Существует масса возможностей приспособить своп

к конкретным желаниям конечного пользователя. Например

в то

вре-

мя

как

условная сумма обычно

не

амортизируется

период действия

свопа, можно учесть

их

амортизацию; свопы можно заключать

опци-

оном

на

возможное удлинение

или

укорачивание

их

продолжитель-

ности

(tenor);

свопы можно заключать

отсроченным назначением

(setting)

свопового купона

и т. д.

Смысл нашего обсуждения состоит

в том, что все

структуры сво-

пов основаны

на

одной

и той же

базисной модели. Варьируя условия

свопа, комбинируя свопы

или

комбинируя свопы

другими инстру-

ментами, можно разработать огромное количество новых структур.

Тем

не

менее

все

свопы очень легко понять, раскладывая

их на со-

ставляющие элементы.

Роль свопового дилера

Взрывной характер увеличения количества свопов

был бы

невоз-

можен

без

переквалификации своповых брокеров

своповых диле-

ров.

Своповый дилер всегда готов заключить своп

качестве контра-

гента

и с

одинаковым энтузиазмом сыграть

при

этом роль платель-

щика

или

получателя фиксированной ставки. Своповый дилер полу-

чает прибыль

от

своего бид-аск спреда

на

стороне

фиксированной

ставкой свопового купона.

В отличие

от

прямого свопа между двумя конечными пользовате-

лями, своповый дилер вовсе

не

должен добиваться соответствия всех

условий первого свопа

контрагентом

условиям второго свопа

контрагентом

/?.

Более того, своповый дилер вовсе

не

должен немед-

ленно получить

свое распоряжение контрагента

В,

чтобы заклю-

чить своп

контрагентом

А.

«Фокус» заключается

в том, что

свопо-

вый дилер должен соответствующим образом хеджировать свою

об-

щую подверженность риску, связанную

со

всеми

его

операциями.

Иными словами, своповый дилер старается поддерживать сбаланси-

рованность своих операций,

но как

только возникают какие-нибудь

дисбалансы,

он

будет

их

хеджировать.

Для того чтобы хеджировать эффективно, своповые дилеры нуж-

даются

ликвидном кредитном рынке,

на

котором торгуют низкори-

сковыми формами долговых обязательств

непрерывным множест-

вом сроков погашения. Одним

из

кредитных рынков, удовлетворяю-

щих всем этим требованиям, является рынок казначейских ценных

бумаг

США.

Поэтому если своповый дилер заключает процентный

своп

как

плательщик фиксированной ставки против ставки

6-М

LIBOR,

он попросту продает «шорт» соответствующее количество 6-месяч-

ных казначейских векселей

использует выручку

для

покупки сред-

364

несрочных

или

долгосрочных казначейских облигаций. Рассмотрим

пример. Своповый дилер вступает

контакт

клиентом

—

фирмой,

которой нужен процентный своп

на

сумму

в 25

млн. дол.

сроком

на

пять лет, причем фирма хочет платить плавающую ставку,

получать

фиксированную. Своповый дилер соглашается платить клиенту

9,26%

(sa) на 25 млн. дол. в

обмен

на

уплату клиентом дилеру ставки

6-М

LIBOR

на 25 млн. дол. Эта

ситуация представлена

на рис. 13.15.

Рис.

13.15.

Денежные потоки между

1-м

контрагентом

и своповым банком

Своповый дилер немедленно хеджирует, продавая

по

номиналу каз-

начейские векселя

на 25

млн. дол.

используя поступления

от

такой

«короткой» продажи

для

покупки

по

номиналу

на 25 млн. дол.

5-летних казначейских облигаций

(рис. 13.16).

Своповый дилер

те-

перь хеджирован.

На

практике своповый дилер

общем случае хед-

жирует

помощью казначейских фьючерсов,

но

также можно

ис-

пользовать хеджирование

на

наличном рынке. Заметим,

что

хеджи-

рование оставляет своповому дилеру некоторый базисный риск

на

стороне

плавающей процентной ставкой. Дилер получает ставку

LIBOR

платит ставку казначейского векселя. Коль скоро измене-

ния ставки LIBOR

изменения ставки казначейских векселей будут

не точно коррелированы между собой

(а так оно и

бывает), остается

некоторый базисный риск.

Рис.

13.16.

Денежные потоки после «зачета»

на рынке государственных ценных бумаг

365

Когда своповый дилер подбирает подходящий своп или, по край-

ней мере, подбирает часть условной основной суммы в первом свопе,

он тут же увеличивает на соответствующую сумму свой хедж в казна-

чейских ценных бумагах (или в казначейских фьючерсах). Поэтому,

постоянно корректируя таким способом свои наличные и фьючерс-

ные рыночные позиции, своповый дилер может эффективно вести

свою своповую бухгалтерию, чрезмерно не заботясь о мэтчинге от-

дельных свопов.

Использование рынков ценных бумаг для хеджирования свопо-

вых операций помогает понять, почему своповые дилеры оценивают

свопы именно так, а не иначе. Свопы, особенно долгосрочные (со

сроком от двух лет и больше), обычно оцениваются прибавлением

спреда к ставкам казначейских ценных бумаг с эквивалентным сред-

ним сроком «жизни»

. Например, своповый дилер может «делать ры-

нок» 5-летних процентных свопов «фиксированная ставка/плаваю-

щая ставка», назначая в качестве ставки продавца (цена «аск» —

дилер получает фиксированную ставку) ставку 5-летних казначейских

облигаций плюс 62 базисных пункта, а в качестве цены покупателя

(цена «бид» — дилер платит фиксированную ставку) — ставку 5-летних

казначейских облигаций плюс 52 базисных пункта. Так обе цены вы-

ражаются через свой спред по отношению к казначейским бумагам с

эквивалентным средним сроком. Краткосрочные же свопы, т. е. сво-

пы со сроком в два (иногда три) года и меньше, часто оцениваются

по евродолларовому стрипу рынка ΙΜΜ с помощью процедуры, род-

ственной использовавшейся при оценивании контрактов FRA. Такая

процедура была рассмотрена нами в главе 12.

Как уже отмечалось, процентные и валютные опционы часто ис-

пользуются в сочетании со свопами с целью создания интересных

конструкций. В следующих двух главах мы рассмотрим опционы и их

применение.

Резюме

Своп — это такое соглашение между двумя сторонами, когда пер-

вая согласна производить выплаты второй по фиксированной ставке

процента, а вторая сторона соглашается платить первой стороне по

плавающей ставке. Свопы стали действительно революционным эта-

пом финансовой инженерии. За первые 11 лет после их появления

оборот условных сумм этих инструментов вырос с незначительной

суммы до более чем 2,5 трлн. дол. (к концу 1990 г.).

Свопы имеют множество применений. Их можно использовать для

хеджирования многопериодных ценовых рисков, снижения издержек

финансирования, освоения новых рынков и создания синтетических

инструментов. Рынок свопов организуется своповыми дилерами, ко-

366

торые предлагают эти продукты банкам, небанковским коммерческим

организациям, сберегательным учреждениям, нефинансовым корпо-

рациям и правительству. Три наиболее распространенных свопа —

это процентный своп, валютный своп и товарный своп. Хотя в этой

главе и не обсуждались фондовые свопы, но они тоже стали приме-

няться в последнее время. (Фондовые свопы обсуждаются в главе 23.)

Простейшие свопы — в основном те их виды, которые были раз-

работаны первыми, — сейчас относятся к так называемым «простым»

процентным свопам. До их появления, однако, масса вариантов ви-

доизменялась, приспосабливаясь к специфическим, иногда уникаль-

ным, потребностям. Варианты свопов можно создавать, модифици-

руя условия самого свопа или комбинируя своп с каким-либо другим

инструментом. Часто таким инструментом становится многопериод-

ный опцион.

Своповые дилеры «складируют» у себя свопы и ведут своповую

бухгалтерию. Они стараются сбалансировать свои своповые опера-

ции, чтобы устранить риски, проистекающие от мисмэтча свопов.

Если свопы нельзя сбалансировать, то дилерам приходится приме-

нять хеджирование. Хеджирование может происходить на наличном

рынке или с помощью производных инструментов, включая фьючер-

сы и форварды. Дилер старается получить прибыль от бид-аск спре-

да. Дилерские спреды резко уменьшились за те годы, когда конку-

ренция в финансовой индустрии привела к трансформации свопов

от продуктов с небольшим объемом сделок и высокой маржей до про-

дуктов со значительным объемом сделок и низкой маржей.

Примечания

'Читатель, заинтересованный в более подробном изучении свопов и их

приложений, вариантов свопов, способов их оценивания, документации по

свопам и управления портфелем свопов, должен посмотреть

Marshal!

and

Kapner

(1990).

Читателя, интересующегося, кроме того, взаимосвязью сво-

пов с другими производными инструментами, можно отослать к работе

Kap-

ner and

Marshall

(1990).

Мы предполагаем, что процентные разницы для немецких марок и про-

центные разницы для долларов можно непосредственно суммировать. Мы

также предполагаем, что разницы с фиксированной и плавающей ставкой

для одной и той же валюты тоже аддитивны. Все эти предположения не вполне

корректны, но мы немного потеряем, используя их для иллюстрации обсуж-

даемых понятий. Необходимые же корректировки в полном объеме изложе-

ны в

Kapner

and

Marshall

(1990).

Там же.

Свопы оцениваются с помощью казначейских ценных бумаг, которые

являются неамортизационными инструментами. Средний срок «жизни» не-

амортизационного инструмента равен сроку действия. То же справедливо и

367

для неамортизационных свопов. Однако амортизационные свопы имеют сред-

ний срок «жизни», который короче их срока действия. Поэтому мы пользу-

емся средним сроком «жизни» (а не сроком действия), когда определяем со-

ответствующие казначейские обязательства для оценивания свопов.

Ссылки и рекомендуемая литература

М. Arak, A.

Estrella,

Goodman,

and A.

Silver.

«Interest

Rate

Swaps:

An Alter-

native

Explanation*,

Financial

Management

(Summer

1988),

pp.

12—18.

Aspel, J.

Cogen,

and M.

Rabin.

«Η

edging

Long

Term

Commodity

Swaps

with

Futures*,

Global Finance Journal (Fall

1989),

pp.

77—93.

Bicksler

and A.

Chen.

«An

Economic

Analysis

Interest

Rate

Swaps», Journal

Finance

(July

1986),

pp.

645-655.

Felgren.

«Interest

Rate

Swaps:

Use,

Fisk,

and Prices», New England Economic

Review,

Federal

Reserve

Bank

Boston

(November

1987),

pp.

22—32.

Herbst.

«Hedging

Against

Price

Index

Inflation with

Futures

Contracts*,

Journal

Futures Markets (Winter

1985),

pp.

489-504.

Hull.

Options,

Futures and

Other

Derivative Securities,

Englewood

Cliffs,

NJ:

Prentice

Hall,

1989.

Kapner

and J. Marshall. The

Swaps

Handbook,

New York: New York

Institute

Finance,

1990.

J. Marshall, V.

Bansal,

and A.

Tucker.

«Swaps as a

Cash

Management

Tool», work-

ing

paper,

St.

John's

University (March

1991).

Marshall

and K.

Kapner.

Understanding

Swap

Finance, Cincinnati, OH:

South-

western,

1990.

Marshall

and A.

Tucker.

«Equity

Derivatives:

The

Plain

Vanilla Equity

Swap

and

Its

Variants*,

working

paper,

St.

John's

University

(February

1991).

Park.

«Сиггепсе

Swaps

as a

Long-Term

International

Financing

Technique*,

Journal of

International

Business

Studies

(Winter

1984),

pp.

47—54.

C. Smith, C.

Smithson,

and L.

Wakeman.

«The Evolving

Market

for

Swaps*,

Mid-

land Corporate Finance Journal (Winter

1986),

pp.

20—32.

C. Smith, C.

Smithson,

and L.

Wakeman.

«The

Market

for

Interest

Rate

Swaps*,

Financial

Management

(Winter

1988),

pp.

34-44.

Tucker.

Financial Futures,

Options,

and

Swaps,

St.

Paul,

MN:

West

Publishing,

1991.

S. Turnball. «Swaps: A

Zero

Sum

Game*,

Financial

Management

(Spring

1987),

pp.

15-22.

Wall. «Interest

Rate

Swaps

in an

Agence

Theoretic

Model with

Uncertain

Inter-

est

Rates*,

working

paper

№

86—6,

Federal

Reserve

Bank

Atlanta

(July

1986).

Wall and J.

Pringle.

«Alternative

Explanations

Interest

Rate

Swaps*,

working

paper

№ 87-2,

Federal

Reserve

Bank

of Atlanta

(April

1987).

Глава 14

Однопериодные опционы: коллы и путы

Обзор

Инструменты, которые мы будем обсуждать в этой и следующей

главах, отличаются от других финансовых инструментов тем, что все

они в некотором смысле позволяют сделать выбор

(option).

Опцион —

это контракт между двумя сторонами, в котором одна сторона имеет

право, но не обязательство что-либо сделать — обычно купить или

продать один из базисных активов.

Понятие опциона — довольно общее. Самые известные типы опци-

онов — это коллы и путы. Опцион «колл» (или колл-опцион; call

option)

гарантирует лицу, его приобретшему, право (но не обязатель-

ство) купить определенный базовый актив, тогда как опцион «пут»

(пут-опцион; put

option)

гарантирует его покупателю право (но не

обязательство) продать некоторый базовый актив. Только покупатель

колла или пута имеет право без обязательства. Продавец контракта

имеет абсолютное обязательство.

Коллы и путы — не только виды опционов. Например, многие

облигации имеют характеристики опционного типа. Наиболее часто

встречаются две из этих характеристик — конвертируемость

(conversion

feature),

ассоциирующаяся с конвертируемыми облигациями, и «от-

зываемость» (call

feature),

связанная с «отзываемыми» облигациями.

Конвертируемая облигация — это облигация, держатель которой имеет

право, но не обязательство конвертировать облигацию в некоторый

другой актив того же эмитента. «Отзываемая» облигация — это такая

облигация, которую эмитент имеет право, но не обязательство пога-

сить до истечения срока.

Так как права без обязательств имеют свою цену, покупатель опци-

она должен заплатить его продавцу за опцион или опционоподобную

характеристику — нельзя получить ценность, не отдавая ценности.

В случае коллов и путов цена, уплаченная за опцион, имеет просто

форму некоторой суммы, которая оплачивается вперед и называется

премией

(premium).

В случае конвертируемой облигации покупатель

369

получает опционоподобную характеристику как часть облигации й

оплачивает опцион косвенно, в виде уменьшения купона. Это зна-

чит, что владелец облигации платит по номиналу в момент выпуска,

но получает купон ниже текущего рыночного на срок действия обли-

гации. Следовательно, плата за опцион производится частями, в те-

чение срока действия облигации. «Отзываемость» облигации понять

чуть сложнее. Держатель облигации владеет облигацией, но эмитент

облигации владеет опционом. Поэтому, когда инвестор покупает об-

лигацию у эмитента, он одновременно продает эмитенту опцион. За

этот опцион эмитент платит покупателю облигации. В этом случае

платеж имеет вид купона, который выше текущего рыночного — по

отношению к «неотзываемой» облигации — на срок действия обли-

гации. И снова платеж за опцион производится частями в течение

«жизни» облигации.

Существует много других типов опционов и опционоподобных ха-

рактеристик, соответствующих финансовым инструментам. В этой

главе мы сфокусируем внимание на старейших и простейших типах

опционов, а именно коллах и путах, и уже более кратко на опционо-

подобных характеристиках, которые иногда связаны с облигациями.

Все эти опционы являются однопериодными в том смысле, что они

действуют в течение одного определенного периода. В следующей

главе мы изучим многопериодные опционы.

Оценивание опционов — один из наиболее сложных в математи-

ческом отношении вопросов во всех прикладных финансовых обла-

стях. Первая завершенная модель оценивания опциона

(option

pricing

model

(ОРМ) была разработана Ф. Блэком и М. Шоулзом и опубли-

кована в 1973 г. Первая модель Блэка-Шоулза имела ограниченную

сферу применения в том, что касалось типов опционов, которые мож-

но было оценить, типов активов, на которые продавались опционы,

и поведения цены базового актива во времени. Последующие иссле-

дования, основанные на оригинальной модели Блэка-Шоулза, и мно-

жество вариантов ОРМ привели к появлению других видов опцио-

нов,

других базовых активов и других типов поведения цен. В боль-

шинстве случаев продвинутые версии моделей оценивания опционов

в математическом плане опираются на сложные вероятностные кон-

струкции, и рассматривать эти модели без серьезной подготовки в

вопросах, связанных с таким сложнейшим аппаратом, в лучшем слу-

чае представляется опрометчивым

. Однако это не такая уж серьез-

ная проблема, так как все вычисления, необходимые для определе-

ния справедливой рыночной стоимости опционов, уже автоматизи-

рованы и имеется соответствующее программное обеспечение для

обычных вычислительных машин и для микрокомпьютеров

. По этим

причинам мы не будем изучать математический аппарат, используе-

мый в моделях оценивания опционов.

370