Маршалл Дж.Ф., Бансал В.К. Финансовая инженерия Полное руководство по финансовым нововведениям

Подождите немного. Документ загружается.

срока погашения,

но

вовсе

не для

всех источников денежных пото-

ков.

Чаще бывает

так,

что

инвестиции, включая

инвестиции

про-

изводство товаров, продаваемых

на

конкурентных рынках, дают

до-

ходности, подверженные риску. Вследствие этого

финансовой дея-

тельности стало общепринятым использовать термин «доходность»,

или «ожидаемая доходность», понимая

под

этим средний процент-

ный доход, связанный

некоторой позицией,

использовать термин

«риск», имея

виду

при

этом стандартное отклонение процентного

дохода, связанного

позицией. Также общепринятым стало относить

эти доходности

периоду

один

год,

независимо

от

фактической

длины базового периода. После этого

уже

будет уместным интерпре-

тировать ожидаемую доходность

как

среднюю ставку дохода

(mean

rate of

return),

риск

— как

стандартное отклонение ставки дохода

(standard

deviation

of the rate of

return).

Как мы

вскоре убедимся,

та-

кая трактовка может

не

всегда быть удобной

случае, когда инвести-

ционный горизонт длиннее

или

короче,

чем I год.

Количественные аспекты портфельного анализа

В последующем изложении

мы не

будем требовать, чтобы рас-

сматриваемый период

был

равен году,

поэтому

нам

необязательно

интерпретировать доходность

как

годовую ставку дохода. Подразу-

мевается,

что все

доходности выражены

процентной форме.

Тем не

менее

мы

предполагаем,

что все

доходности рассматриваются

за

один

период

—

мы

лишь

не

интересуемся длиной этого единственного

пе-

риода. Пока

мы

будем считать,

что

безрисковые активы отсутствуют.

Портфель

— это

просто совокупность активов.

каждым активом

портфеля связаны средняя доходность

дисперсия доходности. Кроме

того,

каждой парой доходностей связан коэффициент корреляции.

Коэффициентом корреляции доходностей измеряют степень линей-

ной корреляции между двумя доходностями. Коэффициент корреля-

ции должен находиться

пределах

от -1 до +1. В

любом

из

крайних

случаев

мы

имеем полную корреляцию.

случае

полной корреляци-

ей флуктуации доходности одного актива полностью определяются

флуктуациями доходности другого актива. Если коэффициент корре-

ляции равен

+1, то

говорят,

что

доходности полностью положительно

коррелированы, если

он

равен

-I,

то

говорят,

что

доходности пол-

ностью отрицательно коррелированы. Естественно,

что

доходность

лю-

бого актива полностью положительно коррелирована сама

собой.

Если корреляция доходностей

не

совпадает

с -1 или +1, то

гово-

рят,

что

доходности

не

полностью (частично) коррелированы. Если

коэффициент корреляции находится посредине между двумя край-

ними значениями,

т. е. он

равен нулю,

то

говорят,

что

доходности

не

коррелированы.

151

Чтобы различать активы портфеля между собой, нам нужно вве-

сти соответствующую индексацию. Кроме того, нам нужно еще вве-

сти обозначения для коэффициента корреляции. Мы обозначим до-

ходность актива / через л, среднее величины г. через μ. и дисперсию

г. через σ

. Мы будем обозначать корреляцию между доходностями

актива / и актива j через Г

i,j

(ро).

Как и в случае со средними и дисперсиями, коэффициенты кор-

реляции вычисляются с помощью электронных таблиц, статистиче-

ских пакетов и специальных калькуляторов. Для подсчета коэффи-

циента корреляции нам нужно сначала вычислить ковариацию меж-

ду двумя доходностями. Ковариация между доходностями актива / и

актива j обозначается через с... Формула для вычисления а., дается

соотношением 6.4, а коэффициент корреляции рассчитывается через

ковариацию и стандартные отклонения по формуле 6.5.

Теперь у нас есть все необходимое для получения средней доход-

ности и дисперсии доходности для портфеля активов в целом. Обо-

значим доходность портфеля через r

, среднюю доходность портфеля

через μ

и дисперсию доходности портфеля через с \ Нам осталось

решить, каким образом взвешивать различные активы при их вклю-

чении в состав портфеля. Мы обозначим вес актива / через w

и будем

считать, что всего в портфель включено η активов. Сумма использу-

емых нами весов должна равняться единице

(100%).

(Если сумма ве-

сов меньше единицы, то это означает, что мы допускаем, чтобы часть

средств оставалась без дела.) Характеристики портфеля связаны с ха-

рактеристиками отдельных доходностей (средними, дисперсиями и

коэффициентами корреляции) формулами 6.6, 6.7 и 6.8 соответст-

венно

(6.4)

(6.5)

(6.6)

(6.7)

(6.8)

152

Доходность портфеля г и средняя доходность портфеля μ

легко

интерпретируются. Обе эти величины являются взвешенными сред-

ними соответствующих характеристик для отдельных активов. Более

сложно воспринять смысл дисперсии доходности σ

. Она является

суммой произведений (каждое из которых состоит из пяти сомножи-

телей).

Первые два сомножителя в произведении являются весами,

вторые два — стандартными отклонениями, а последний сомножи-

тель представляет собой коэффициент корреляции. Эти произведе-

ния подсчитываются для любой пары / и

у.

Всего под знаками сумми-

рования должно быть η · η или η

таких произведений.

Формулу 6.8 можно упростить (при этом уменьшится объем необ-

ходимых вычислений), если учесть два обстоятельства. Во-первых,

при совпадении i и j произведение w

i,j

превращается в w

Это происходит в силу того, что корреляция любой доходности с самой

собой, по определению, равна единице. Во-вторых, при разных i и j

произведения w

. равны между собой и их мож-

но один раз включить в сумму с удвоением коэффициента. Имея это

в виду, можно переписать формулу 6.8 в виде формулы 6.9.

Хотя два различных способа представления дисперсии портфеля

дают один и тот же результат, есть определенные преимущества в

использовании именно соотношения 6.9. При таком разложении дис-

персии более отчетливо видно, что портфельный риск состоит из двух

различных компонент. Первая, помеченная цифрой «1», определяет

риск, связанный только с дисперсиями отдельных доходностей. Этот

риск называется несистематическим риском (иногда о нем говорят

как о специфическом риске). Вторая компонента риска, помеченная

цифрой «2», определяет риск, связанный с корреляциями между до-

ходностями активов, включенных в портфель. Этот риск называется

систематическим риском (иногда его называют также рыночным

риском).

Значение разделения риска на несистематический и систематиче-

ский состоит в том, что эти виды риска ведут себя совершенно по-

разному, когда количество активов, включаемых в портфель, увели-

чивается. Предположим, что различные активы, включаемые в порт-

фель,

имеют примерно одинаковые веса. Положим w

= 1/n, тогда с

расширением портфеля несистематический риск становится все мень-

ше (на языке статистики мы говорим, что риск асимптотически при-

ближается к нулю). Поведение несистематического риска представ-

лено на рис. 6.2.

(6.9)

153

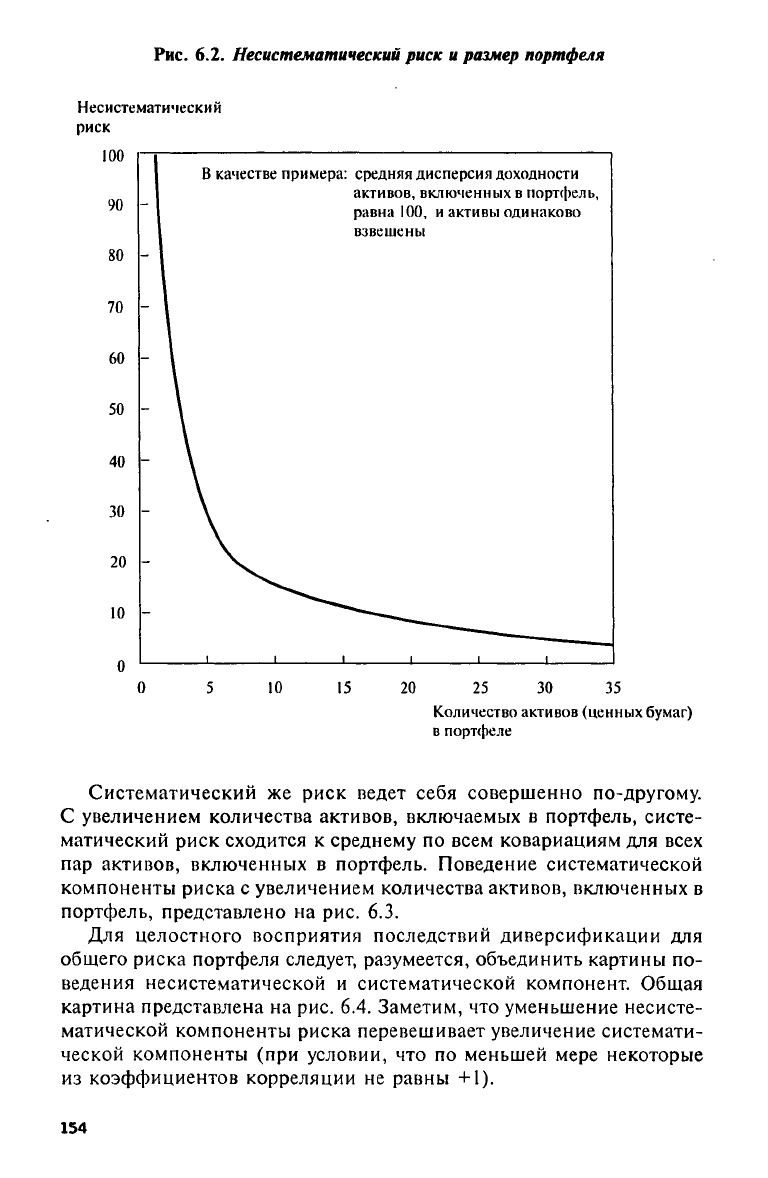
Рис. 6.2. Несистематический риск и размер портфеля

Систематический же риск ведет себя совершенно по-другому.

С увеличением количества активов, включаемых в портфель, систе-

матический риск сходится к среднему по всем ковариациям для всех

пар активов, включенных в портфель. Поведение систематической

компоненты риска с увеличением количества активов, включенных в

портфель, представлено на рис. 6.3.

Для целостного восприятия последствий диверсификации для

общего риска портфеля следует, разумеется, объединить картины по-

ведения несистематической и систематической компонент. Общая

картина представлена на рис. 6.4. Заметим, что уменьшение несисте-

матической компоненты риска перевешивает увеличение системати-

ческой компоненты (при условии, что по меньшей мере некоторые

из коэффициентов корреляции не равны +1).

154

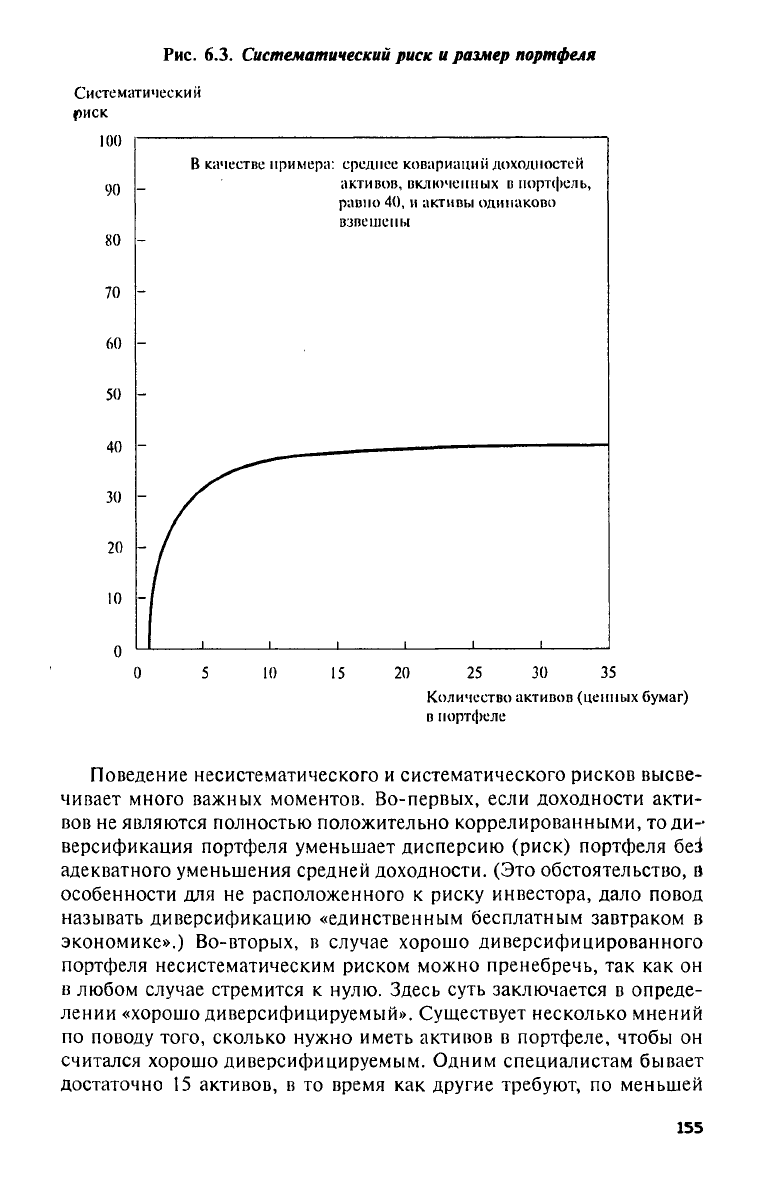
Рис.

6.3. Систематический риск и размер портфеля

Поведение несистематического и систематического рисков высве-

чивает много важных моментов. Во-первых, если доходности акти-

вов не являются полностью положительно коррелированными, то ди-

версификация портфеля уменьшает дисперсию (риск) портфеля бе4

адекватного уменьшения средней доходности. (Это обстоятельство, в

особенности для не расположенного к риску инвестора, дало повод

называть диверсификацию «единственным бесплатным завтраком в

экономике».) Во-вторых, в случае хорошо диверсифицированного

портфеля несистематическим риском можно пренебречь, так как он

в любом случае стремится к нулю. Здесь суть заключается в опреде-

лении «хорошо диверсифицируемый». Существует несколько мнений

по поводу того, сколько нужно иметь активов в портфеле, чтобы он

считался хорошо диверсифицируемым. Одним специалистам бывает

достаточно 15 активов, в то время как другие требуют, по меньшей

155

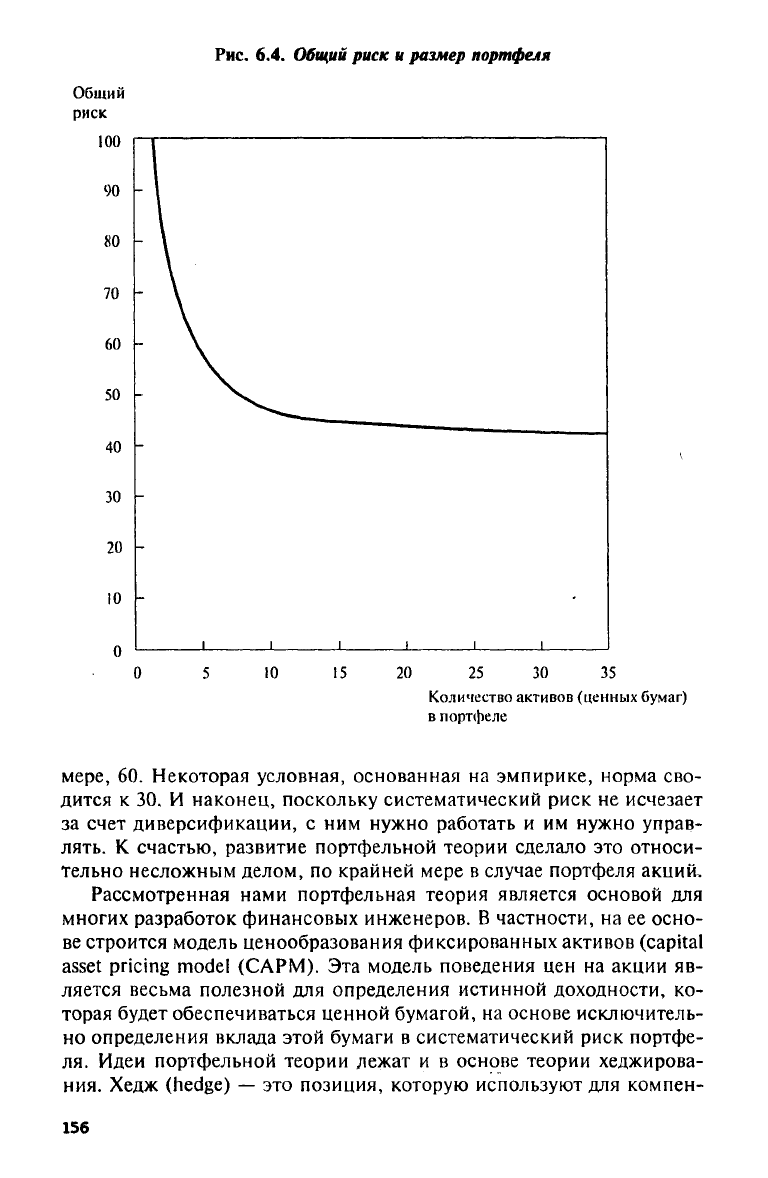
Рис.

6.4.

Общий

риск и размер портфеля

мере,

60.

Некоторая условная, основанная

на

эмпирике, норма сво-

дится

к 30. И

наконец, поскольку систематический риск

не

исчезает

за счет диверсификации,

с ним

нужно работать

и им

нужно управ-

лять.

счастью, развитие портфельной теории сделало

это

относи-

тельно несложным делом,

по

крайней мере

случае портфеля акций.

Рассмотренная нами портфельная теория является основой

для

многих разработок финансовых инженеров.

частности,

на ее

осно-

ве строится модель ценообразования фиксированных активов

(capital

asset

pricing

model

(САРМ).

Эта

модель поведения

цен на

акции

яв-

ляется весьма полезной

для

определения истинной доходности,

ко-

торая будет обеспечиваться ценной бумагой,

на

основе исключитель-

но определения вклада этой бумаги

систематический риск портфе-

ля.

Идеи портфельной теории лежат

и в

основе теории хеджирова-

ния. Хедж

(hedge)

— это

позиция, которую используют

для

компен-

156

сации ценового риска, связанного с какой-либо другой позицией (на-

зываемой наличной позицией). Хедж только тогда бывает эффектив-

ном, когда доходности хеджирующего инструмента и доходности на-

личной позиции коррелированы. Чем сильнее коррелированы эти до-

ходности (неважно — положительно или отрицательно), тем более

эффективным будет хедж. (Это приложение портфельной теории бо-

лее подробно рассматривается в следующей главе.)

Нерасположенность к риску и портфельный анализ

В главе 4 утверждалось, что основным постулатом финансовой те-

ории является то обстоятельство, что рационально действующий субъ-

ект не расположен к риску. Иными словами, рациональные люди

(с «правильными» функциями полезности) не любят рисковать. Од-

нако вместе с тем мы говорили, что не все субъекты одинаково не

расположены к риску. Некоторые совсем не расположены к риску и

совсем не хотят рисковать, чтобы получить доходность выше сред-

ней. Другие не расположены к риску в умеренной степени и готовы

подвергать себя риску для получения доходности выше средней. Пер-

вых мы будем называть консервативными в финансовом отношении,

а вторых — агрессивными. Теперь мы рассмотрим такое отношение к

риску в более формальном плане и сделаем это в контексте порт-

фельной теории.

Во-первых, предположим, что нам удалось построить множество

портфелей, которые для каждого уровня доходности характеризуют-

ся наименьшим риском. Это множество портфелей называется мно-

жеством минимальной дисперсии. Можно показать, что множество

минимальной дисперсии для портфелей имеет квадратичную форму

и на графике выглядит как парабола. Эффективное множество порт-

фелей является подмножеством множества минимальной дисперсии,

которое лежит выше точки портфеля с минимальной дисперсией

(minimum

variance

portfolio (MVP), рис, 6.5. Эти портфели построены

в координатах «риск-доходность» (на вертикальной оси откладыва-

ется средняя доходность, а на горизонтальной — стандартное откло-

нение). В каждый заданный момент времени получаемое эффектив-

ное множество портфелей может рассматриваться как отражение те-

кущего состояния экономики.

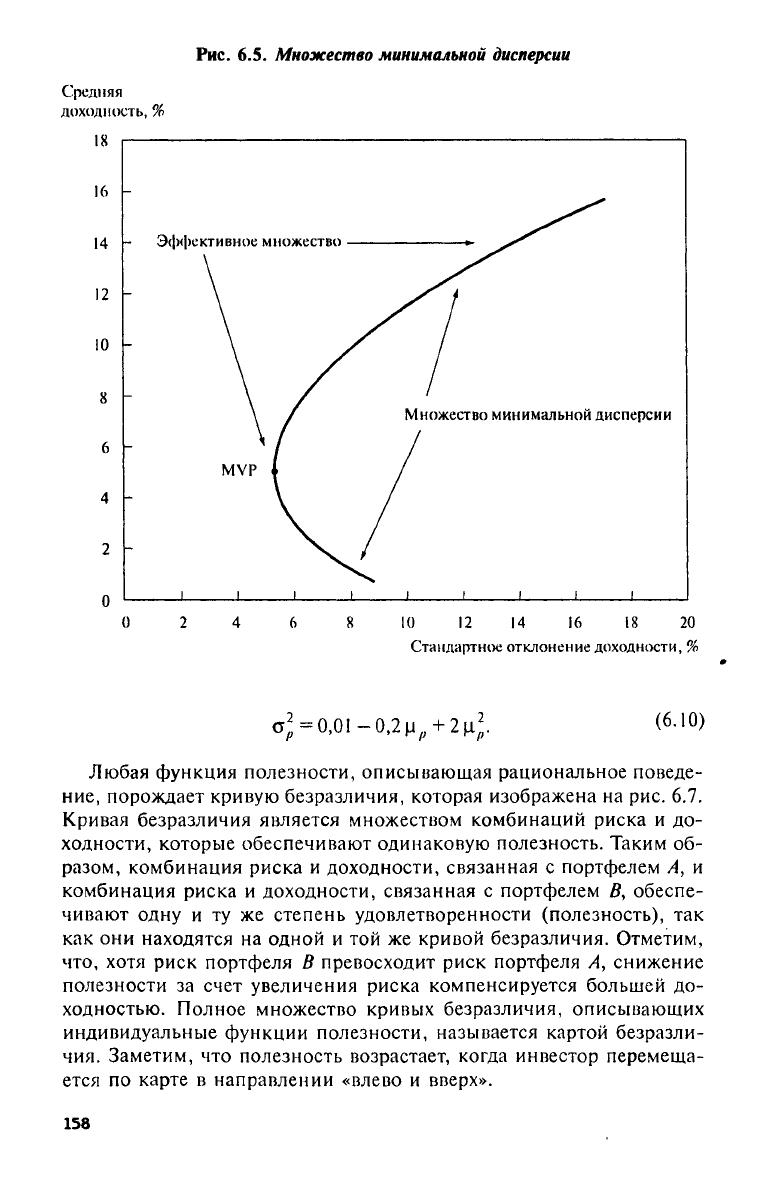
В качестве примера для изображения на графике типичного эф-

фективного множества мы воспользуемся квадратичной зависимостью,

задаваемой соотношением 6.10, и ограничимся рассмотрением тех

портфелей, которые лежат выше портфеля с минимальной дисперси-

ей.

Эффективное множество представлено на рис. 6.6.

157

(6.10)

Любая функция полезности, описывающая рациональное поведе-

ние,

порождает кривую безразличия, которая изображена на рис. 6.7.

Кривая безразличия является множеством комбинаций риска и до-

ходности, которые обеспечивают одинаковую полезность. Таким об-

разом, комбинация риска и доходности, связанная с портфелем А, и

комбинация риска и доходности, связанная с портфелем В

обеспе-

чивают одну и ту же степень удовлетворенности (полезность), так

как они находятся на одной и той же кривой безразличия. Отметим,

что,

хотя риск портфеля В превосходит риск портфеля А, снижение

полезности за счет увеличения риска компенсируется большей до-

ходностью. Полное множество кривых безразличия, описывающих

индивидуальные функции полезности, называется картой безразли-

чия. Заметим, что полезность возрастает, когда инвестор перемеща-

ется по карте в направлении «влево и вверх».

158

Рис. 6.5. Множество минимальной дисперсии

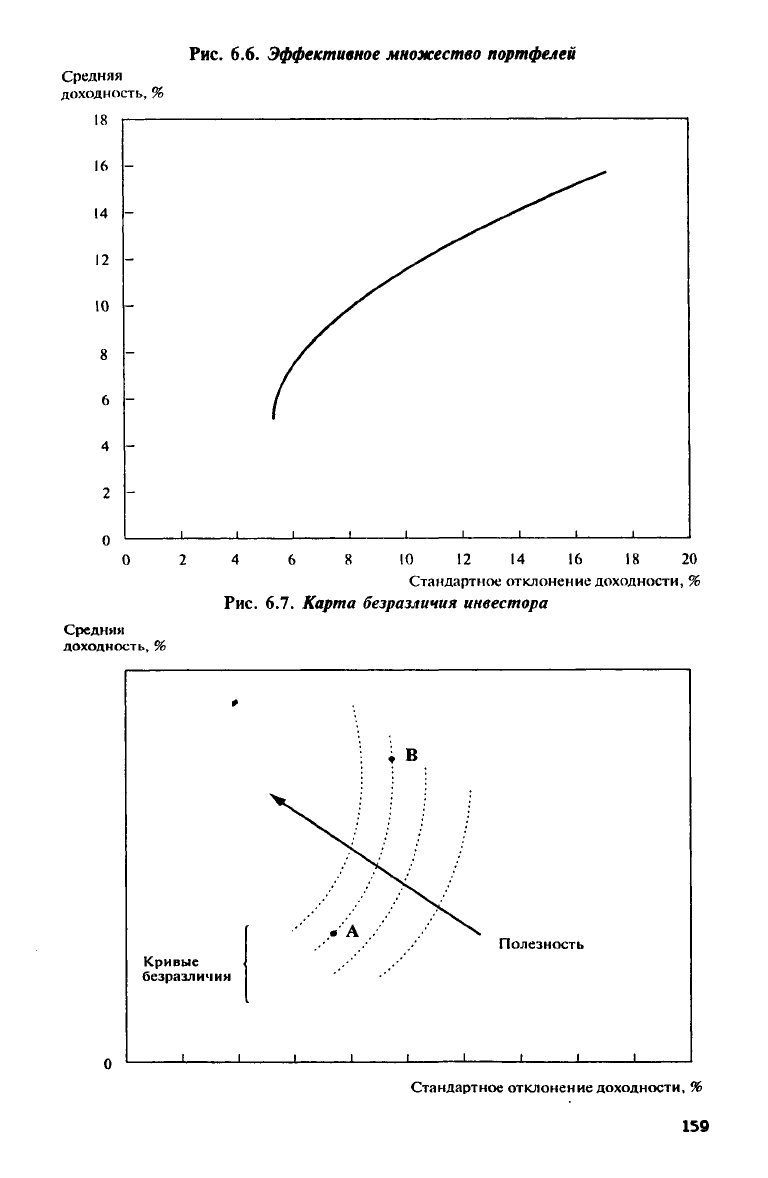
Рис. 6.6. Эффективное множество портфелей

Рис. 6.7. Карта безразличия инвестора

159

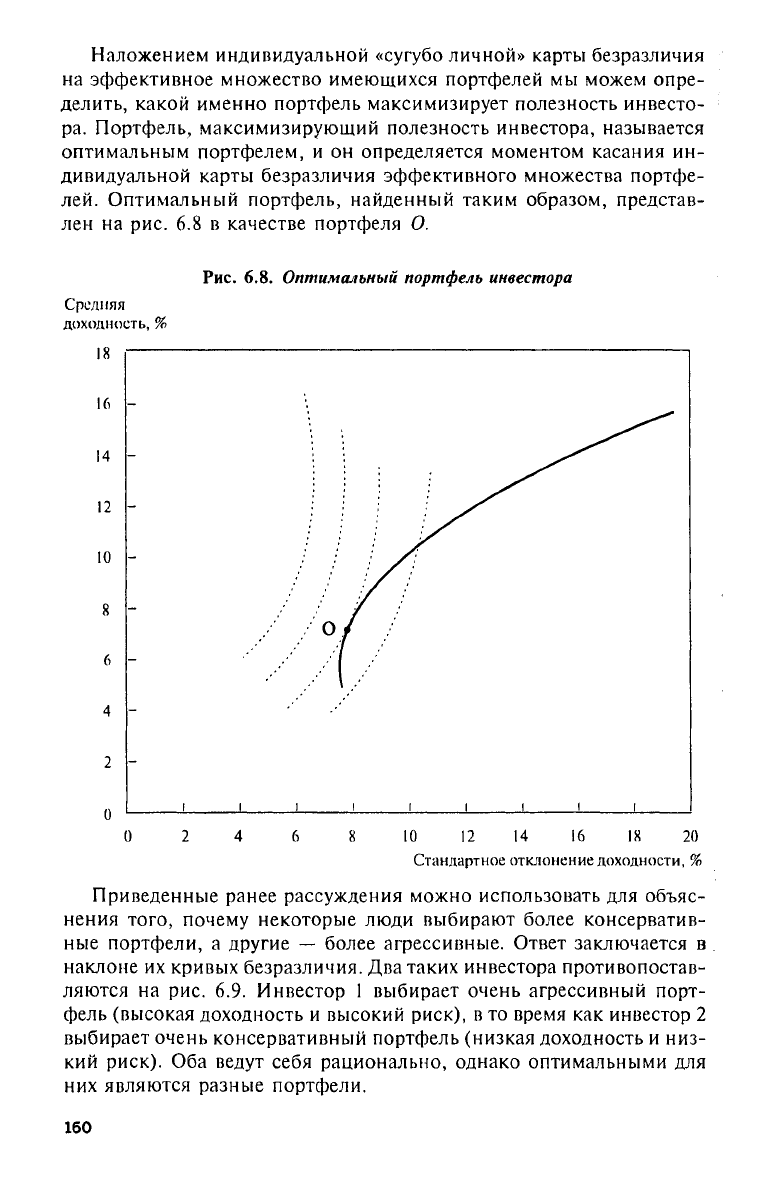
Наложением индивидуальной «сугубо личной» карты безразличия

на эффективное множество имеющихся портфелей мы можем опре-

делить, какой именно портфель максимизирует полезность инвесто-

ра. Портфель, максимизирующий полезность инвестора, называется

оптимальным портфелем, и он определяется моментом касания ин-

дивидуальной карты безразличия эффективного множества портфе-

лей. Оптимальный портфель, найденный таким образом, представ-

лен на рис. 6.8 в качестве портфеля О.

Рис.

6.8. Оптимальный портфель инвестора

Приведенные ранее рассуждения можно использовать для объяс-

нения того, почему некоторые люди выбирают более консерватив-

ные портфели, а другие — более агрессивные. Ответ заключается в

наклоне их кривых безразличия. Два таких инвестора противопостав-

ляются на рис. 6.9. Инвестор 1 выбирает очень агрессивный порт-

фель (высокая доходность и высокий риск), в то время как инвестор 2

выбирает очень консервативный портфель (низкая доходность и низ-

кий риск). Оба ведут себя рационально, однако оптимальными для

них являются разные портфели.

160