Маршалл Дж.Ф., Бансал В.К. Финансовая инженерия Полное руководство по финансовым нововведениям

Подождите немного. Документ загружается.

Инвестиция А обеспечивает больший суммарный денежный по-

ток, чем инвестиция В. В предположении одинаковых начальных за-

трат инвестиция А обеспечивает больший доход (или меньший ущерб,

что,

по сути, одно и то же), чем инвестиция В (в терминах обычного

бухгалтерского учета). Но это вовсе не означает, что инвестиция А

предпочтительнее инвестиции В с финансовой точки зрения.

Временная стоимость

Финансовая стоимость денежных потоков рассмотренных ранее

инвестиций А и В не совпадает с прибылью от этих потоков, рассчи-

танной по правилам бухгалтерского учета, поскольку финансовая

оценка потоков в отличие от бухгалтерской обязательно учитывает

временной фактор. Другими словами, время имеет свое измерение, и

эта мера должна быть, безусловно, учтена при оценке денежных по-

токов. Время принимается во внимание для того, чтобы привести

разновременные денежные потоки к единому временному эквива-

ленту. Эти нормированные по времени стоимости называются теку-

щими (приведенными) стоимостями

(present

value).

Для того чтобы привести (дисконтировать) денежные потоки к

текущим стоимостям, необходимо знать ставку дисконтирования. На

языке экономистов подходящая ставка дисконтирования — это не

что иное, как возможная стоимость денег при их использовании в

инвестициях, альтернативных рассматриваемой. К примеру, так как

денежные потоки известны нам с полной определенностью (соглас-

но сделанному ранее предположению), вполне приемлемо использо-

вать в качестве ставки дисконтирования доходность, предоставляе-

мую сберегательным вкладом, таким, как вложение в казначейские

облигации с подходящим сроком погашения. Доходность, которую

обеспечивают казначейские облигации, может рассматриваться как

альтернативная стоимость денег, вложенных в инвестиции А и В.

Процедура расчета текущей стоимости денежного потока несколько

осложняется тем, что нам следует учесть эффект сложных процентов.

Это так, поскольку полученные денежные средства могут и должны

быть реинвестированы (если только не используются на цели потреб-

ления). Мы будем обозначать денежные средства, полученные в мо-

мент /, через CF

, а ставку дисконтирования, применяемую к денеж-

ному потоку в момент /, — через к

Текущая стоимость этого денеж-

ного потока определяется уравнением 4.1 я или эквивалентным ему

уравнением 4.1b.

101

(4.1 о)

(4.16)

Для разных денежных потоков вовсе

не

обязательно используется

одна

и та же

ставка дисконтирования. Более того, имеются очень

серьезные основания считать,

что

разновременные денежные потоки

следует дисконтировать

по

разным ставкам.

Тем не

менее

приве-

денных далее примерах

мы

будем предполагать общую ставку дискон-

тирования

для

всех денежных потоков.

Пусть доходность казначейских облигаций

подходящим сроком

погашения составляет

10%. Мы

можем вычислить приведенную сто-

имость первого денежного потока

от

инвестиции

следующим обра-

зом:

Приведенная стоимость второго потока

от

инвестиции

вычис-

ляется аналогично:

Процесс повторяется

до тех пор,

пока

не

будут рассчитаны

все

денежные потоки.

Все

потоки

от

инвестиций

А и В

вместе

с их

теку-

щими стоимостями отображены

табл.

4.2.

Таблица

4.2.

Денежные потоки, дисконтированные

по

ставке

10%

(в

дол.)

Инвестиция

Год

Объем

Текущая стоимость Год

Объем Текущая стоимость

500

454,55

900

818,18

600

495,87

600

495,87

700 525,92

500 375,66

800

546,41

400

273,21

Итого

2600

2022,75

Итого

2400

1962,92

Все денежные потоки имеют некоторую приведенную стоимость.

Поскольку

эти

приведенные стоимости отнесены

одному

тому

же

моменту времени

(к

текущему моменту),

они

могут быть сопоставле-

ны

по

величине

и,

следовательно, просуммированы. Суммирование

приведенных стоимостей позволяет дать общую оценку совокупно-

сти потоков. Сумма приведенных стоимостей обычно представляется

102

с использованием специального математического знака суммы (урав-

нение

4.2 —

стандартная форма).

(4.2)

Уравнение

4.2

подразумевает,

что

приведенная стоимость каждого

из денежных потоков рассчитывается отдельно

затем

все эти

стои-

мости суммируются.

Как

следует

из

табл.

4.2, это

дает

для

инвести-

ции

оценку

2022,75 дол., а для

инвестиции

В — 1962,92 дол. Эти

цифры нуждаются

своей трактовке. Текущая стоимость инвестиции

А показывает,

что нам

можно согласиться вложить

данный проект

до

2022,75 дол., но не

более. Аналогичным образом текущая стои-

мость инвестиции

указывает

на то, что в

этот проект можно согла-

ситься вложить

до 1962,92 дол., но не

более.

В связи

этим имеет смысл поговорить

затратах. Очень часто,

хотя

и не

всегда, затраты

на

инвестиционный проект сводятся

еди-

новременному вложению средств

(в

момент

0).

Предположим,

что

для реализации каждого

из

проектов достаточно

момент

вложить

1200

дол.

Так как

текущая стоимость находящихся сейчас

наличии

1200 дол.

должна составлять

те же 1200 дол.,

нетрудно понять,

что

любой денежный поток

момент

будь

то

исходящий поток, такой,

как затраты,

или

входящий поток, такой,

как

доход, должен иметь

приведенную стоимость, равную номинальному размеру потока.

Та-

ким образом, соответствующая величина непосредственно добавля-

ется

сумме (если

она

положительная)

или

вычитается

из

суммы

(если отрицательная)

уже

рассчитанных приведенных стоимостей.

Разность между суммой текущих стоимостей денежных потоков,

индуцированных данной инвестицией,

начальными затратами

на-

зывается чистой текущей (приведенной) стоимостью

(net present

value).

Чистая текущая стоимость, часто обозначаемая аббревиатурой

NPV,

постоянно используется

для

анализа

сравнения вариантов инве-

стирования.

примеру,

NPV

инвестиции

составляет

822,75

дол.,

NPV инвестиции

равна

762,92 дол.

Очевидно,

что

инвестиция

предпочтительнее инвестиции

В.

Поскольку сделанный ранее временной анализ стоимостей состо-

ит

приведении сумм, которые должны быть получены

будущие

периоды,

текущему моменту времени,

он

носит название расчета

(исчисления) текущей (приведенной) стоимости

(present value

arithmetic).

Однако иногда бывает удобнее производить расчет

про-

тивоположном направлении.

Это

означает,

что мы

имеем определен-

ную текущую сумму, предназначенную

для

инвестирования,

жела-

ем узнать,

во что она

превратилась

бы в

какой-то будущий момент

103

времени, если бы приносила периодический доход по некоторой из-

вестной ставке. Такой тип задач оценки стоимости во времени назы-

вается расчетом будущей стоимости

(future

value)

или конечной сто-

имости

(terminal

value).

Будущая стоимость (обозначенная FV) на-

чальной суммы (обозначенной PV, поскольку приведенная стоимость

суммы в момент 0 совпадет с ее номинальным значением) представ-

лена равенством 4.3.

(4.3)

Величина г в равенстве 4.3 соответствует процентной ставке, а ве-

личина t — количеству будущих периодов, на которое мы проециру-

ем изучаемую стоимость. Процентная ставка из равенства 4.3 выпол-

няет ту же функцию, что и ставка дисконтирования в равенстве 4.1.

В самом деле, если вы внимательно посмотрите на равенства 4ЛЬ и

4.3 и подставите в формуле 4.16 PV вместо CF, то убедитесь, что эти

два равенства по сути — одно и то же. Единственное реальное отли-

чие здесь в знаке, который отрицателен перед количеством периодов

в случае текущей стоимости и положителен в случае будущей стои-

мости. Это различие в знаках легко объяснимо. При расчете текущей

стоимости будущая сумма проецируется во времени назад на теку-

щий момент и поэтому время берется с отрицательным знаком. Од-

нако при расчете будущей стоимости сумма проецируется во времени

вперед, отчего берется с положительным знаком. Если признать эк-

вивалентность формулировок текущей и будущей стоимости, то нет

необходимости проводить разграничение между ставкой дисконти-

рования и процентной ставкой. На самом деле в большинстве обла-

стей финансовой практики мы обходимся без такого разграничения

понятий и попросту называем их единым термином — «доходность»

(yield). Аналогичным образом нам нет необходимости различать ис-

числение текущей и будущей стоимостей, и мы будем объединять их

общим понятием «исчисление» (расчет) стоимостей

(valuation

arithmetic).

Анализ чувствительности временной стоимости

Один из наиболее интересных аспектов использования чистой при-

веденной стоимости как меры эффективности капиталовложений за-

ключается в высокой чувствительности этой меры к изменению став-

ки дисконтирования. Это означает, что даже если денежные потоки

полностью известны, то NPV инвестиции будет колебаться вместе с

колебаниями ставки дисконтирования. Рассмотрим, например, что

произойдет с NPV инвестиций А и В, если ставка дисконтирования

будет не 10, а 25%. Новые значения текущей стоимости вместе с

предыдущими представлены в табл. 4.3.

104

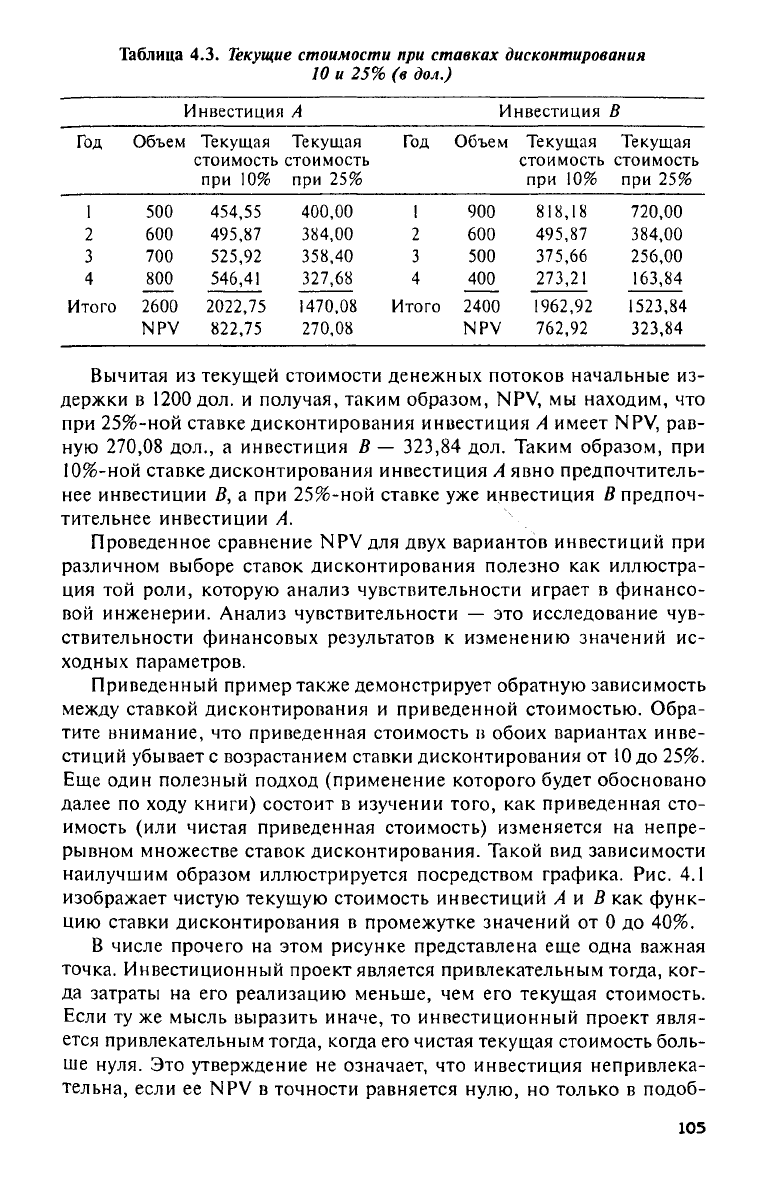
Таблица

4.3.

Текущие

стоимости при ставках дисконтирования

и 25% (в дол.)

Инвестиция

Год

06beiv

ι Текущая

Текущая

Год

Объем

Текущая

стоимость стоимость стоимость стоимость

при

10%

при

25%

при

10%

при

25%

500

454,55

400,00

900

818,18

720,00

600 495,87

384,00

600

495,87

384,00

700

525,92 358,40

500

375,66

256,00

800

546,41

327,68

400

273,21

163,84

Итого

2600

2022,75

1470,08

Итого

2400

1962,92 1523,84

NPV

822,75

270,08

NPV

762,92

323,84

Вычитая

из

текущей стоимости денежных потоков начальные

из-

держки

в 1200

дол.

получая, таким образом,

NPV, мы

находим,

что

при 25%-ной ставке дисконтирования инвестиция

имеет

NPV,

рав-

ную

270,08

дол., а

инвестиция

В — 323,84 дол.

Таким образом,

при

10%-ной ставке дисконтирования инвестиция

явно предпочтитель-

нее инвестиции

В, а при

25%-ной ставке

уже

инвестиция

предпоч-

тительнее инвестиции

А.

Проведенное сравнение

NPV для

двух вариантов инвестиций

при

различном выборе ставок дисконтирования полезно

как

иллюстра-

ция

той

роли, которую анализ чувствительности играет

финансо-

вой инженерии. Анализ чувствительности

— это

исследование чув-

ствительности финансовых результатов

изменению значений

ис-

ходных параметров.

Приведенный пример также демонстрирует обратную зависимость

между ставкой дисконтирования

приведенной стоимостью. Обра-

тите внимание,

что

приведенная стоимость

обоих вариантах инве-

стиций убывает

возрастанием ставки дисконтирования

от 10 до 25%.

Еще один полезный подход (применение которого будет обосновано

по

ходу книги) состоит

изучении того,

как

приведенная сто-

имость

(или

чистая приведенная стоимость) изменяется

на

непре-

рывном множестве ставок дисконтирования. Такой

вид

зависимости

наилучшим образом иллюстрируется посредством графика.

Рис. 4.1

изображает чистую текущую стоимость инвестиций

А и В как

функ-

цию ставки дисконтирования

промежутке значений

от 0 до 40%.

В числе прочего

на

этом рисунке представлена

еще

одна важная

точка. Инвестиционный проект является привлекательным тогда, ког-

да затраты

на его

реализацию меньше,

чем его

текущая стоимость.

Если

ту же

мысль выразить иначе,

то

инвестиционный проект явля-

ется привлекательным тогда, когда

его

чистая текущая стоимость боль-

ше нуля.

Это

утверждение

не

означает,

что

инвестиция непривлека-

тельна, если

ее NPV в

точности равняется нулю,

но

только

подоб-

105

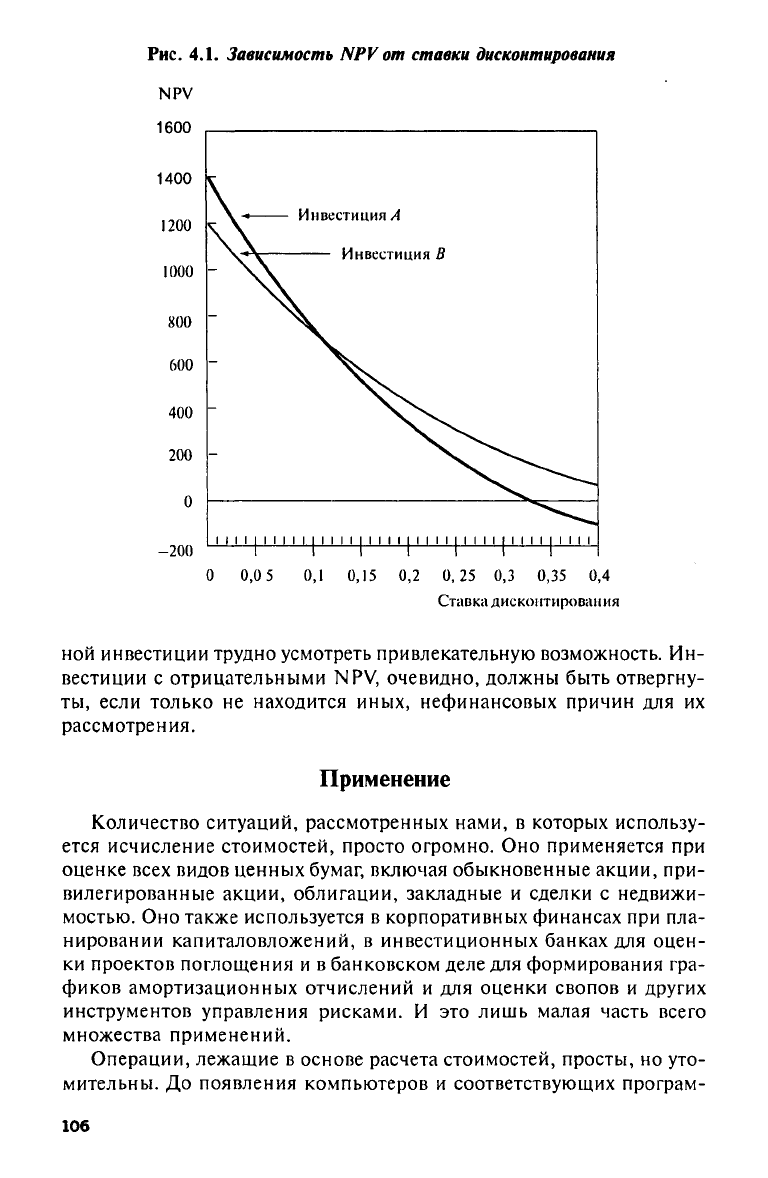
Рис. 4.1. Зависимость NPV от ставки дисконтирования

ной инвестиции трудно усмотреть привлекательную возможность. Ин-

вестиции с отрицательными NPV, очевидно, должны быть отвергну-

ты,

если только не находится иных, нефинансовых причин для их

рассмотрения.

Применение

Количество ситуаций, рассмотренных нами, в которых использу-

ется исчисление стоимостей, просто огромно. Оно применяется при

оценке всех видов ценных бумаг, включая обыкновенные акции, при-

вилегированные акции, облигации, закладные и сделки с недвижи-

мостью. Оно также используется в корпоративных финансах при пла-

нировании капиталовложений, в инвестиционных банках для оцен-

ки проектов поглощения и в банковском деле для формирования гра-

фиков амортизационных отчислений и для оценки свопов и других

инструментов управления рисками. И это лишь малая часть всего

множества применений.

Операции, лежащие в основе расчета стоимостей, просты, но уто-

мительны. До появления компьютеров и соответствующих програм-

106

мных пакетов единственным средством уменьшить поток утомитель-

ных вычислений было прибегнуть к использованию таблиц. Были раз-

работаны многочисленные типы таблиц для расчета текущей и буду-

щей стоимости 1 дол. при различных вариантах значений ставок и

количества периодов. В своей простейшей форме эти таблицы обес-

печивали расчет текущей и будущей стоимости для ставок и перио-

дов,

выраженных целыми числами (1%, 2%, 3% 1, 2, 3 ...). Пробле-

ма, однако, состояла в том, что существует очень мало реальных за-

дач,

которые можно сформулировать в категориях целых периодов и

без дробных процентов. Единственно разумным решением здесь бы-

ло либо иметь набор значительно более подробных таблиц (которые

принимали форму табличных справочников), либо использовать тех-

нику аппроксимации, так называемую интерполяцию. Этот послед-

ний подход повсеместно преподавался (и продолжает преподаваться)

в школах бизнеса. Студенты изучают математическую процедуру по-

иска промежуточной точки между двумя целыми процентными став-

ками или двумя целыми периодами. \

Недостаток интерполяционного метода состои¥^ том, что линей-

ная техника применяется к нелинейным соотношениям. Это неиз-

бежно приводит к погрешностям. Хотя некоторые профессора дока-

зывают, что возникающая ошибка мала и ею можно пренебречь, в

реальной жизни при крупных сделках мизерная в пересчете на 1 дол.

ошибка может обернуться потерей больших денег. Кроме того, мно-

гие современные арбитражные операции представляют собой попыт-

ки извлечь выгоду из очень незначительных расхождений между ры-

ночной и справедливой ценой одного или нескольких инструментов.

Под справедливой ценой понимается текущая стоимость совокупно-

сти денежных потоков при известной ставке дисконтирования. Не-

большие ошибки могут приводить к серьезным искажениям в оценке

эффективности стратегий.

Пример подобной ошибки, вызванной неточностями интерполя-

ции, представлен на рис. 4.2. На график нанесены две точки, соот-

ветствующие приведенной стоимости 1000 дол. при ставках в 8% и

9% и сроке возврата в 10 лет. Кривая, соединяющая эти точки, изо-

бражает истинную приведенную стоимость тех же 1000 дол. при став-

ках между 8 и 9%. Заметим, что зависимость приведенной стоимости

от ставки дисконтирования является нелинейной. Теперь предполо-

жим, что нас интересует приведенная стоимость, рассчитанная при

ставке 8,5%. Поскольку отдельным значением точка 8,5% в простых

таблицах не представлена, мы получим соответствующую приведен-

ную стоимость посредством интерполяции известных значений в точ-

ках 8 и 9%. Согласно графику, искомая величина находится в сред-

ней точке прямой, соединяющей значения приведенной стоимости

при 8 и 9%. Эта средняя точка отличается от истинного значения

стоимости на величину, которая также указана на графике.

107

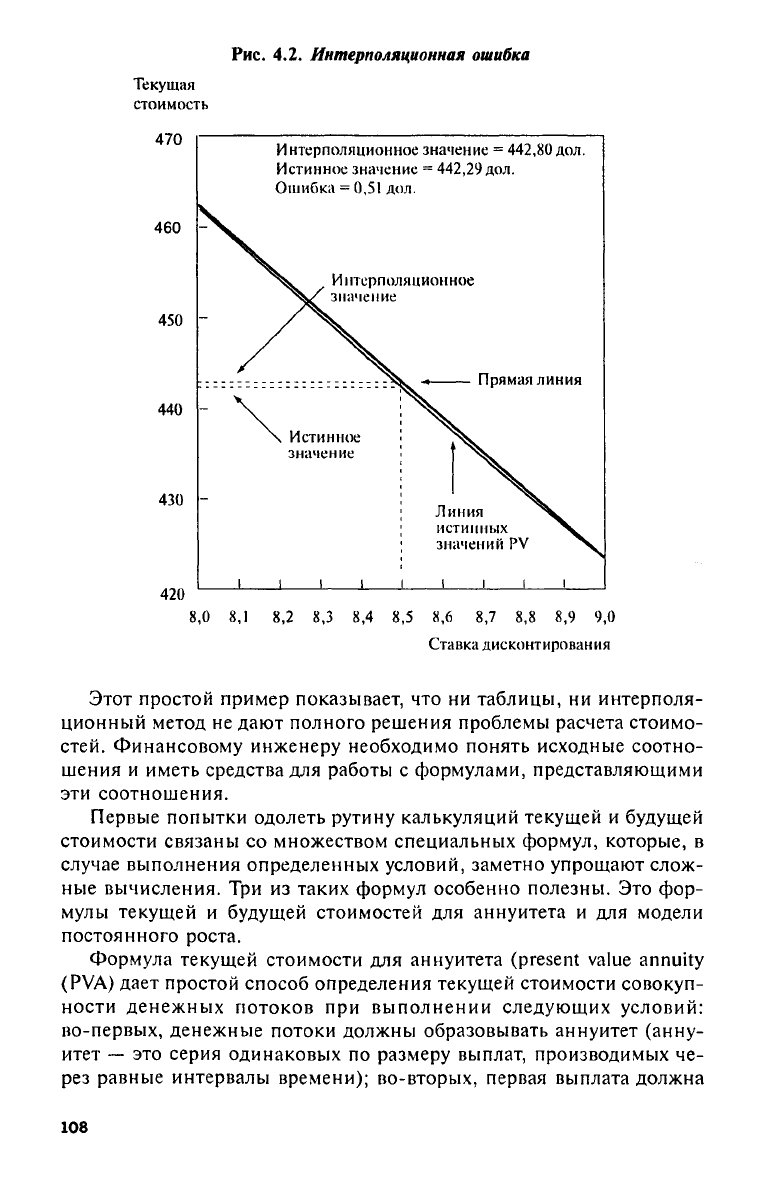
Рис.

4.2.

Интерполяционная ошибка

Этот простой пример показывает,

что ни

таблицы,

ни

интерполя-

ционный метод

не

дают полного решения проблемы расчета стоимо-

стей. Финансовому инженеру необходимо понять исходные соотно-

шения

иметь средства

для

работы

формулами, представляющими

эти соотношения.

Первые попытки одолеть рутину калькуляций текущей

будущей

стоимости связаны

со

множеством специальных формул, которые,

случае выполнения определенных условий, заметно упрощают слож-

ные вычисления.

Три из

таких формул особенно полезны.

Это

фор-

мулы текущей

будущей стоимостей

для

аннуитета

и для

модели

постоянного роста.

Формула текущей стоимости

для

аннуитета

(present value annuity

(PVA) дает простой способ определения текущей стоимости совокуп-

ности денежных потоков

при

выполнении следующих условий:

во-первых, денежные потоки должны образовывать аннуитет (анну-

итет

— это

серия одинаковых

по

размеру выплат, производимых

че-

рез равные интервалы времени); во-вторых, первая выплата должна

108

быть произведена ровно через один интервал времени

от

текущего

момента; в-третьих, количество выплат должно быть конечным;

в-четвертых, ставка дисконтирования должна быть одинаковой

для

всех потоков. Если

все эти

условия выполняются,

то

текущая стои-

мость может быть рассчитана

по

следующей формуле:

(4.4)

Свойства аннуитета

требование постоянства ставки дисконти-

рования позволяют

нам

опустить индекс времени

при

величинах

к.

Заметим,

что

если формула

4.4 и не

выглядит заметно проще,

чем формула

4.2, то для

расчетов

она

намного предпочтительнее. Пред-

положим, например,

что

количество денежных потоков

равенстве

4.2

равно

40, т. е. n = 40.

Формула

4.2

потребовала

бы

сделать

общей

сложности

отдельных вычислений

затем произвести окончатель-

ное суммирование. Формула

4.4

приводит

тому

же

результату

по-

средством единственной вычислительной операции.

Вторая формула относится

будущей стоимости

для

аннуитета

(future value annuity

(FVA).

этом случае

нас

интересует будущая сто-

имость серии равномерных вкладов

некоторый инвестиционный

инструмент, проводимых

по

фиксированной процентной ставке

в те-

чение всего периода действия инструмента. Вклады должны произ-

водиться через равные промежутки времени,

первый

из них

должен

быть сделан ровно через один временной интервал

от

текущего

мо-

мента.

Нас

интересует стоимость совокупности денежных потоков

на

момент последней выплаты. Если

все

указанные условия выполне-

ны,

то

будущая стоимость совокупности денежных потоков рассчи-

тывается

так:

(4.5)

Последняя

из

рассматриваемых нами ситуаций относится

такой

серии денежных потоков,

которой размер потоков

от

периода

периоду возрастает

некоторым фиксированным коэффициентом

ро-

ста, обозначаемым здесь через

Предполагается,

что

последователь-

ность денежных потоков бесконечна, потоки возникают через рав-

ные промежутки времени

дисконтируются

по

одной

и той же

став-

ке.

Если

эти

условия выполнены,

то

текущая стоимость всей сово-

купности денежных потоков вычисляется

так:

(4.6)

109

Формулу

4.6

иногда называют моделью постоянного роста.

этом

случае

для

расчетов достаточно использовать только один поток

—

поток первого периода, обозначенный здесь через

Особо можно отметить специальную форму равенства

4.6,

кото-

рая возникает

случае, когда коэффициент роста

равен нулю. Если

= 0, то

денежные потоки, соответствующие модели постоянного

роста, принимают форму неограниченного

во

времени аннуитета.

В этом случае равенство

4.6

сводится

равенству

4.7.

(4.7)

Модель

бесконечным временным горизонтом очень полезна

при

оценке таких бессрочных аннуитетов,

как

привилегированные акции

с фиксированным дивидендом

бессрочные долговые обязательства

с фиксированным купоном. Последние

не

играли существенной

ро-

ли

на

рынке капиталов

США, но

выпускались

были популярны

на

европейских рынках.

Электронные таблицы (спредшиты)

Великим благом

для

финансового анализа

финансовой инжене-

рии стало появление

широкое распространение компьютерных элек-

тронных таблиц. Такие популярные пакеты,

как Lotus 1-2-3 (Lotus

Development Corporation) и Excel

(Microsoft), обладают сходной струк-

турой

близки

по

своим возможностям.

Они

позволяют изучать

оценивать сложные совокупности денежных потоков

удивительной

скоростью

легкостью.

Они же

предоставляют эффективные сред-

ства

для

анализа чувствительности.

Мы

не

станем подробно останавливаться

на

использовании элек-

тронных таблиц, отметим лишь,

что

мало

кто из

финансовых инже-

неров согласился

бы

расстаться

этим полезным инструментом. Мно-

гие

из

моделей, подготовленных нами

для

этой книги,

в том

числе

анализ стоимостей, представленный

на рис. 4.1,

были созданы

с ис-

пользованием электронных таблиц.

Расчет сложных процентов

Во многих, если

не в

большинстве, случаях оценки стоимости

ис-

пользуется техника сложных процентов.

Это

ситуации, когда денеж-

ные потоки возникают чаще,

чем

период, относительно которого опре-

делена процентная ставка

или

ставка дисконтирования. Процентная

ставка

(и

ставка дисконтирования),

как

правило, устанавливается

на

период

один

год. Шаг

расчета сложных процентов иногда предва-

110