Алексеев Д.В. Конспекты по общему курсу математики

Подождите немного. Документ загружается.

Матрицы и системы линейных уравнений 9

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

bzz

bzzz

000







В этом случае последняя строка расширенной матрицы соответствует невозможному ра-

венству и, поэтому, система решений не имеет.

2) Матрица коэффициентов после преобразований принимает треугольный вид и число

ненулевых строк расширенной матрицы равно числу неизвестных.

bzz

bzzz







В этом случае мы получаем «лестницу», при помощи которой можно последовательно оп-

ределить все неизвестные, начиная с нижней строки. То есть система имеет единственное

решение.

3) Расширенная матрица имеет вид трапеции, (последняя ненулевая строка матрицы ко-

эффициентов имеет не менее двух ненулевых элементов).

bzz

bzzz

bzzzz







В этом случае, в отличие от предыдущего, последнее уравнение системы содержит не од-

но, а несколько неизвестных. Следовательно, этому уравнению удовлетворяет бесконеч-

ное множество решений. Остальные неизвестные также выражаются через это бесконеч-

ное множество решений. То есть в этом случае система имеет бесконечное множество ре-

шений.

Все эти три качественно различных случая удобно формализовать при помощи понятия

ранга матрицы. Рангом матрицы будем называть число ненулевых строк расширенной

матрицы, которое получается после завершения ее преобразования по алгоритму Гаусса.

Обозначая через

)(AR

ранг матрицы коэффициентов системы, а через

)|( BAR

ранг рас-

ширенной матрицы, приходим к следующим формулировкам.

 Система линейных уравнений не имеет решений, если

)|()( BARAR 

 Система линейных уравнений имеет единственное решение, если

nBARAR  )|()(

- числу искомых неизвестных.

 Система линейных уравнений имеет бесконечное множество решений, если

nBARAR  )|()(

Перечисленные условия на ранги матрицы коэффициентов и ранги расширенной матрицы

называются условиями разрешимости неоднородной системы линейных уравнений.

Условия разрешимости, сформулированные на языке рангов, просто обобщаются на слу-

чай однородных систем линейных уравнений. Поскольку однородная система линейных

уравнений всегда имеет тривиальное решение (все

0

), то сформулировать условие,

при выполнении которого система имеет нетривиальные решения. Это условие равно-

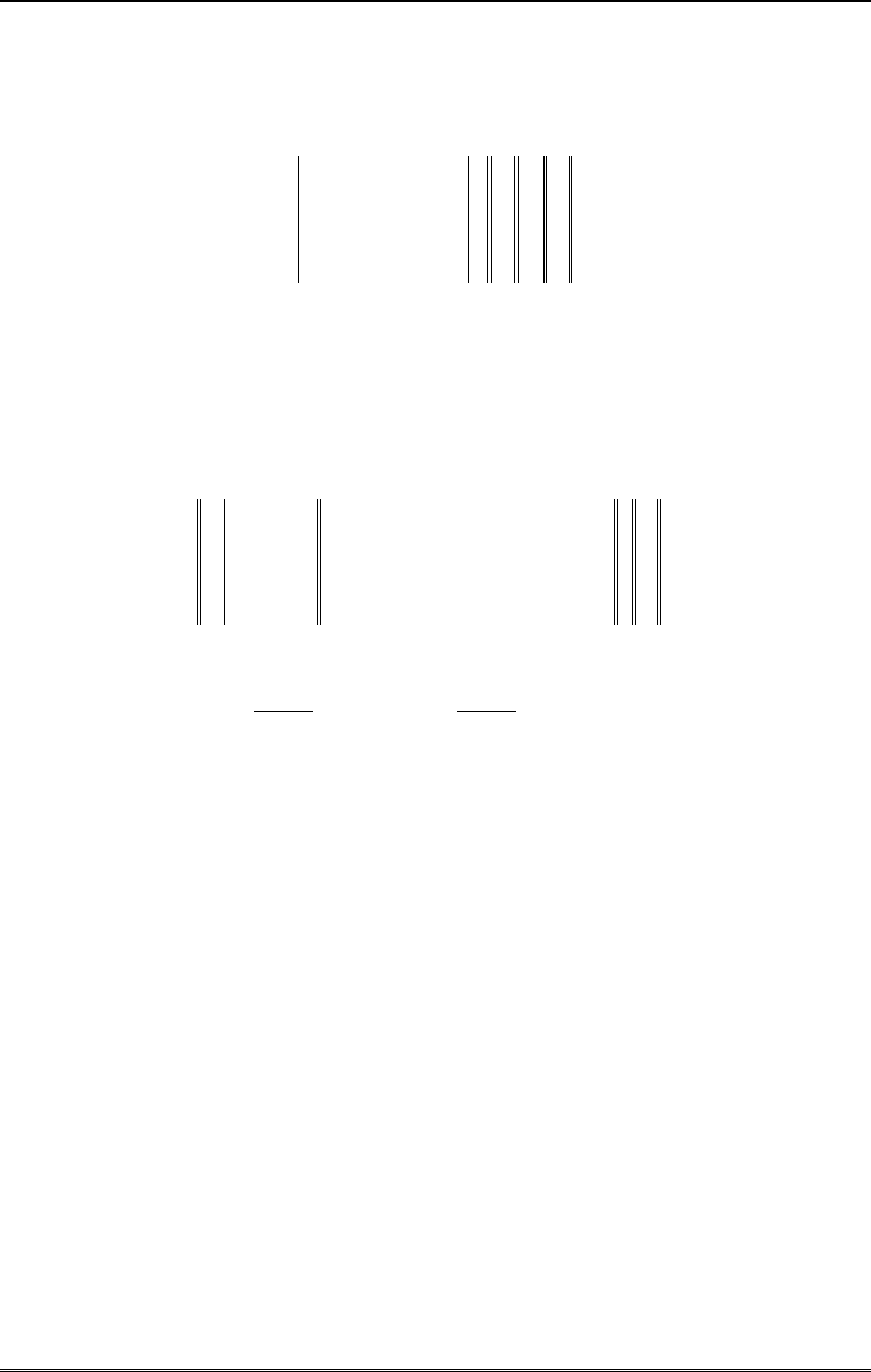
Матрицы и системы линейных уравнений 10

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

сильно условию наличия бесконечного множества решений у неоднородной системы.

Следовательно,

 Однородная система имеет нетривиальные решения если

nAR )(

Пусть система линейных уравнений

nnnnnn

aaa









22221

11211



имеет неособенную матрицу коэффициентов. Тогда эта система имеет единственное ре-

шение и его можно найти при помощи умножения исходной системы уравнений на мат-

рицу, обратную к матрице коэффициентов:

BAXBAAXABAX

111 



В развернутом виде решение системы линейных уравнений при помощи обратной матри-

цы записывается в виде

nnnnn

aaa











22212

12111

)()Ad()Ad(

)Ad()Ad()Ad(

)det(



После выполнения умножения матриц, искомые неизвестные записываются в виде

kjkj

3,2,1,

)det(

)Ad(

)det(











где определители







kjkj

)Ad(

Из последней формулы видно, что



получается из определителя матрицы коэффициен-

тов исходной системы заменой

-го столбца на столбец, стоящий в правой части системы.

Следовательно, искомые решения системы могут быть найдены по формулам

njx

;2;1,/ 

для чего достаточно вычислить определитель матрицы коэффициентов

)det(A

и все

определители



. Эти формулы для решений системы линейных уравнений с неособен-

ной матрицей коэффициентов называются формулами Крамера.

Как видно из приведенного вывода, решение системы линейных уравнений по формулам

Крамера полностью эквивалентно решению при помощи обратной матрицы. Однако, ре-

шение системы линейных уравнений при помощи обратной матрицы является более пред-

почтительным последующим причинам.

 Во-первых, найденная однажды обратная матрица позволяет при помощи матрич-

ного умножения решать любые системы с одинаковой матрицей коэффициентов.

Матрицы и системы линейных уравнений 11

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

 Во-вторых, решение при помощи обратной матрицы может быть применено для

решения матричного уравнения,

BAX 

в котором матрица

является прямо-

угольной.

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Функции одной переменной. Начальные сведения

Бесконечно малые и бесконечно большие функции

Локальные свойства функций

Свойство функции

)(xf

называется локальным, если функция обладает этим свойством

вблизи рассматриваемого значения независимой переменной

ax 

. Слово «вблизи», ис-

пользуемые при формулировке локального свойства, означает следующее:

 если функция определена в точке

ax 

, то значения переменной,

);(



 aax

где



, сколь угодно малое положительное число.

 если функция не определена в точке

ax 

, то

);();(



 aaaax

где



, сколь

угодно малое положительное число.

Это условие, налагаемое на независимую переменную, описывается словами «

стремит-

ся к

», и обозначается символом

ax 

, или

0||  ax

Когда локальное свойство справедливо лишь при значениях независимой переменной,

расположенных с одной стороны от рассматриваемой точки вместо указанных выше дву-

сторонних интервалов используются односторонние интервалы:

 когда

);(



 aax

, пишут



 ax

, и говорят: «

стремится к

справа».

 когда

);( aax





, говорят: «

стремится к

слева», и пишут



 ax

Разновидностью односторонних интервалов, используемых при описании локальных

свойств функции, являются интервалы, задающие большие значения переменной:

 когда

);(  Rx

, где

- сколь угодно большое положительное число, пишут

x

, и говорят «

стремится к плюс бесконечности», или «при больших поло-

жительных значениях переменной»;

 когда

);( Rx 

, пишут

x

, («

стремится к минус бесконечности», или

«при больших отрицательных значениях переменной»);

 когда

);();(  RRx

, пишут

|| x

, и говорят «

стремится к бесконечно-

сти», или «при больших значениях переменной».

Все интервалы, используемые для формулировки локальных свойств функций, приведены

в таблице 1.

Таблица 1 Интервалы, используемые при формулировке локальных свойств функций

Название

Обозначение

Множество изменения переменной

стремится к

ax 

, или

0||  ax

);(



 aax

или

);();(



 aaaax

стремится к

справа



 ax

);(



 aax

стремится к

слева



 ax

);( aax





при больших положительных

x

);(  Rx

при больших отрицательных

x

);( Rx 

при больших

|| x

);();(  RRx

Функции одной переменной. Начальные сведения

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Аналогичные обозначения используются и для интервалов изменения значений функции.

Важно помнить, что при записи соответствующих формул кроме интервала изменения

значений функции всегда необходимо указывать и интервал изменяется ее аргумента.

Например:

 формула



 0||

)(

означает, что для любого сколь угодно большого положи-

тельного числа

можно указать такой интервал

);();(



 aaaa

, в котором

условие

);()(  Rxf

выполняется для всех

);();(



 aaaax

;

 формула

0)(

|| 



означает, что для любого сколь угодно малого положительного

числа



можно указать такой интервал

);();(  RR

, в котором неравенство



|)(| xf

выполняется для всех

);();(  RRx

Бесконечно малые, бесконечно большие и ограниченные функции

Определение бесконечно малой функции.

Функция

)(xf

называется бесконечно малой в точке

, если ее модуль меньше любого

положительного числа в достаточно малой окрестности точки

. Это означает, что исходя

из неравенства



|)(| xf

при любом сколь угодно малом



, можно указать такой интер-

вал

);(



 aa

, в котором данное неравенство выполняется для всех

);(



 aax

Определение бесконечно малой функции записывается при помощи следующих обозначе-

ний:

0|)(|



(модуль функции стремится к нулю при

ax 

), или

0|)(|lim 



(пре-

дельное значение (предел) модуля функции при

ax 

равно нулю).

Аналогично определяется понятие бесконечно малых функций и для других интервалов,

приведенных в таблице 1, уточняя при необходимости и знак бесконечно малой функции.

Например:

 обозначение









0)(lim xf

указывает, что бесконечно малая

0)( xf

при

);(



 aax

;

 обозначение





 0)(lim xf

указывает, что бесконечно малая

0)( xf

при

);( Rx 

Определение бесконечно большой функции.

Функция

)(xf

называется бесконечно большой в точке

если в достаточно малой окре-

стности этой точки ее модуль больше любого положительного числа. Это означает, что

для любого сколь угодно большого числа

можно указать такое

0



, , что неравенство

Rxf |)(|

выполняется для всех

);();(



 aaaax

Удаление точки

ax 

из интервала изменения переменной

сделано потому, что, как

правило, в точке

ax 

рассматриваемая функция не определена.

Определение бесконечно большой функции записывается при помощи обозначений



ax

xf |)(|

, или





)(lim xf

Аналогично определяется понятие бесконечно больших функций и для других интерва-

лов, приведенных в таблице 1, с уточнением при необходимости ее знака. Например:

 обозначение







)(lim xf

указывает, что бесконечно большая функция имеет от-

рицательный знак в интервале

);( aax





;

Функции одной переменной. Начальные сведения

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

 обозначение



x

xf )(

указывает, что бесконечно большая функция положи-

тельна при больших отрицательных значениях переменной.

Среди всех бесконечно больших функций специально выделяют класс бесконечно боль-

ших функций постоянного знака. Про такие функции говорят, что они вблизи рассматри-

ваемой точки имеют бесконечный предел



или



, в соответствии со знаком функ-

ции. Примером бесконечно большой функции, не имеющей определенного предела может

служить функция

xx /)/1sin(

при

0x

Справедливы следующее утверждения, доказательство которых очевидно (надо просто

выписать необходимые неравенства):

 Если функция

)(xf

является вблизи точки

бесконечно большой, то функция

)(/)( xfCxg 

, где

- любая константа, является бесконечно малой вблизи этой

точки;

 Если функция

)(xg

является вблизи точки

бесконечно малой, то функция

)(/)( xgCxf 

является бесконечно большой вблизи этой точки.

Описанная взаимосвязь между бесконечно большими и бесконечно малыми функциями,

для наиболее важного случая бесконечно больших постоянно знака приведена в таблице

Таблица 2 Взаимосвязь между бесконечно малыми и бесконечно большими функциями

Интервал изменения

переменной

Взаимосвязь между функциями

);();(



 aaaax





 0)(lim xf





)(

lim

;





 0)(lim xf





)(

lim

;





)(lim xg





 0

)(

lim

;





)(lim xg





 0

)(

lim

);(



 aax









0)(lim xf







)(

lim

;









0)(lim xf







)(

lim

;







)(lim xg









)(

lim

;







)(lim xg









)(

lim

);( aax













0)(lim xf







)(

lim

;









0)(lim xf







)(

lim

;







)(lim xg









)(

lim

;







)(lim xg









)(

lim

);(  Rx





 0)(lim xf





)(

lim

;





 0)(lim xf





)(

lim

;





)(lim xg





 0

)(

lim

;





)(lim xg





 0

)(

lim

);( Rx 





 0)(lim xf





)(

lim

;





 0)(lim xf





)(

lim

;





)(lim xg





 0

)(

lim

;





)(lim xg





 0

)(

lim

Функции одной переменной. Начальные сведения

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Определение ограниченной функции.

Функция, не являющаяся вблизи рассматриваемой точки бесконечно большой или беско-

нечно малой, называется ограниченной функцией. Это означает, что в интервале, опреде-

ляющем понятие близости к рассматриваемой точке, выполняется неравенство

|)(| cxfc 

, где

,cc

- положительные константы.

Справедливы следующие утверждения, доказательство которых также проводится при

помощи выписывания соответствующих неравенств:

 Сумма ограниченной и бесконечно малой функции является ограниченной функ-

цией

 Сумма ограниченной и бесконечно большой функции является бесконечно боль-

шой функцией

 Произведение ограниченной функции на бесконечно малую функцию является

бесконечно малой функцией

 Произведение ограниченной функции на бесконечно большую функцию является

бесконечно большой функцией

 Деление ограниченной функции на бесконечно большую функцию дает бесконечно

малую функцию

 Деление ограниченной функции постоянного знака на бесконечно малую функцию

постоянного знака дает бесконечно большую функцию.

Операции с бесконечно большими и бесконечно малыми функциями. Неопределенности

Выписывая соответствующие неравенства, нетрудно показать справедливость следующих

утверждений:

 Сумма, разность и произведение бесконечно малых функций является бесконечно

малой функцией

 Произведение бесконечно больших функций и сумма бесконечно больших функ-

ций одинакового знака является бесконечно большой функцией

Оказывается, что других однозначных ответов, при оперировании с бесконечно большими

и бесконечно малыми функциями нет.

Все остальные операции приводят к неопределен-

ным выражениям (кратко, неопределенностям), которые требуется анализировать деталь-

но. Термин неопределенность используется потому, что результат анализа (раскрытия)

неопределенности нельзя предсказать заранее. Например, частное двух бесконечно малых

может оказаться как бесконечно малой, так и ограниченной или даже бесконечно большой

функцией. Ниже перечислены некоторые часто встречающиеся неопределенности, к кото-

рым могут быть сведены более сложные неопределенные выражения.

 Частное двух бесконечно малых

0/0

(нуль делить на нуль), к этой неопределенно-

сти могут быть сведены произведение бесконечно большой и бесконечно малой

функции

0

(нуль умножит на бесконечность)

 Разность бесконечно больших функций одинакового знака



(бесконечность

минус бесконечность) сводится к неопределенности

0

путем вынесения беско-

нечно большого множителя за скобку

 Неопределенности, связанные с возведением в степень

(нуль в степени нуль) и



(единица в степени бесконечность). Обе эти неопределенности сводятся к

0

Мы, естественно, исключаем случаи типа деление бесконечно малой на бесконечно большую, так как они

сводятся к уже перечисленным благодаря взаимосвязи между бесконечно большими и бесконечно малыми.

Функции одной переменной. Начальные сведения

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

при помощи следующего преобразования исходной функции

)))(ln()(exp()(

)(

xfxgxf



Особо выделим принципиально важную неопределенность, называемую «сумма беско-

нечного числа бесконечно малых слагаемых», которая будет подробно рассмотрена в раз-

деле, посвященном представлению функции рядами, - бесконечными суммами.

Непрерывные функции

Функция называется непрерывной, если ее график непрерывная линия. Линия является

непрерывной, если любую пару точек, расположенных на ней, можно переместить в одну

и ту же точку при помощи перемещения по рассматриваемой линии. Для описания близо-

сти точек естественно использовать функцию, выражающую квадрат расстояния между

точками линии

)()( yyxxd 

. Когда точки, расположенные на непрерывной

линии сближаются, расстояние между ними стремится к нулю.

В случае графика функции расстояние между парой его точек выражается формулой

222

))()(()(),( afxfaxaxd 

. Тогда из условия обращения в нуль расстояния при

сближении точек

0),(

axd

, следует, что одновременно выполняются два условия

0||  ax

, и

0|)()(|  afxf

. Это следствие записывается в виде

)()(lim

0||

afxf





, или

0|)()(|

0|| 



afxf

Формальное определение непрерывности функции.

Функция непрерывна в точке

ax 

, если она определена при

);(



 aax

, и

)()(lim

0||

afxf





Из тождества

))()(()()( afxfafxf 

следует важный вывод о структуре непрерывной

функции, - в окрестности любой точки в которой функция непрерывна, она может быть

представлена в виде суммы константы и бесконечно малой функции

xxafxf



 0|)(|),()()(



Это типичный пример формулы, выражающей локальное свойство функции.

Последняя формула используется для анализа неопределенностей, возникающих в форму-

лах функций. Например, функция

)3/()32(

 xxx

не определена при

3x

, но из тож-

дества

)3(4()3/()1)(3(  xxxx

видно, что данная функция имеет вблизи

3x

структуру непрерывной функции, то есть

4)3/()32(





xxx

. Похожая ситуация име-

ет место и для функции

xx /)sin(

при

0x

, так как

1/)sin(

0



Подобные функции обычно «доопределяют по непрерывности», полагая что в точке, где

функция не определена, она равна предельному значению. В то же время, разложение

квадратичной функции на сомножители позволяет преобразовать исходную формулу к

виду, не содержащему неопределенности

1)3/()1)(3(  xxxx

. Со второй дробью

дело несколько сложнее. Ниже будет показано (подробности будут изложены в соответст-

вующем разделе), что синус может быть представлен в виде бесконечной суммы степеней,

- абсолютно сходящегося степенного ряда,

120/6/)sin(

xxxx 

, при этом дробь

120/6/1/)sin(

xxxx 

также является абсолютно сходящимся степенным рядом,

не содержащем неопределенности. Поскольку приведенные формулы получены при по-

мощи тождественных преобразований, нет веских оснований считать, что рассматривае-

мые функции не являются непрерывными. Другими словами, неформальное «доопределе-

Функции одной переменной. Начальные сведения

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

ние функции по непрерывности» сводится к перезаписи исходной формулы функции с

помощью тождественных преобразований в более удобном для рассмотрения виде.

Сравнение бесконечно малых и бесконечно больших функций

Определение символов сравнения

 Говорят, что бесконечно малая функция

0)(



имеет более высокий порядок

малости по сравнению с бесконечно малой функцией

0)(



, если их частное

является бесконечно малой функцией

0)(/)(

xfxf



. Этот факт обозначается

 

)()(

xfoxf

ax



(читается

равно о-малое от

при

ax 

 Говорят, что бесконечно малые функции

0)(



0)(



имеют одинаковый

порядок малости если их частное является ограниченной функцией

Cxfxf

ax

)(/)(

. Этот факт обозначается

 

)()(

xfOxf

ax



(читается

равно о-

большое от

при

ax 

Замечание: символ

 

обозначает ограниченную функцию или константу, а символ

 

любую бесконечно малую функцию.

Бесконечно малые функции одного порядка

 

)()(

xfOxf

ax



называются эквивалентны-

ми, если их разность является бесконечно малой функцией более высокого порядка, чем

сами функции

 

)()()(

221

xfoxfxf

ax



Поскольку бесконечно большие функции связаны с бесконечно малыми функциями при

помощи операции деления, сравнение бесконечно больших функций может быть сведено

к сравнению бесконечно малых.

 Говорят, что бесконечно большая функция



ax

xf |)(|

имеет более высокий поря-

док роста по сравнению с бесконечно большой функцией



ax

xf |)(|

, если их ча-

стное является бесконечно большой функцией



ax

xfxf |)(/)(|

(обозначение

 

)()(

xfoxf

ax



 Говорят, что бесконечно большие функции



ax

xf |)(|



ax

xf |)(|

имеют оди-

наковый порядок роста если их частное является ограниченной функцией

Cxfxf

ax

|)(/)(|

(обозначение

 

)()(

xfOxf

ax



 Говорят, что бесконечно большие функции одного порядка роста

 

)()(

xfOxf

ax



эквивалентны, если

 

1)(/))()((

221

oxfxfxf

ax



Степенной порядок малости и степенной порядок роста

Простейшим примером бесконечно малой функции вблизи точки

ax 

является частный

случай линейной функции

axy 

(равенство

0)(lim 



очевидно!). Поскольку пе-

ременная в данную функцию входит линейно, ее называют бесконечно малой первого по-

рядка. Нетрудно увидеть, что любая натуральная степень бесконечно малой первого по-

Функции одной переменной. Начальные сведения

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

рядка

ax )( 

также будет бесконечно малой функцией

0,0)(lim 



pax

. Такую

функцию называют бесконечно малой порядка

Из описанной выше взаимосвязи бесконечно больших и бесконечно малых функций сле-

дует, что вблизи рассматриваемой точки

ax 

функция

ax )/(1 

является бесконечно

большой, которую естественно назвать бесконечно большой порядка

Показатель степени

, характеризующий рассмотренные выше функции, называют по-

рядком малости, для бесконечно малых, и порядком роста, для бесконечно больших

функций. Из определения сравнения бесконечно больших и бесконечно малых функций

сразу следует, что чем больше показатель степени, тем выше порядок малости для беско-

нечно малой или порядок роста для бесконечно большой функции.

Линейная функция и ее положительные степени также являются примерами бесконечно

больших функций при больших значениях переменной

0,||lim 



, а отрица-

тельные степени, - примерами бесконечно малых функций при больших значениях пере-

менной

0,0||/1lim 



. При этом показатель степени по-прежнему сохраняет на-

звание порядка малости или порядка роста.

Степенные бесконечно малые и бесконечно большие функции важны потому, что при

рассмотрении локальных свойств достаточно широкого класса функций удается записать

для них локальные приближенные формулы именно в виде степенных функций.

Непосредственно из определения символов сравнения

можно получить правила

выполнения алгебраических операций с выражениями, содержащими эти символы. Наи-

более часто используются формулы, приводимые ниже.

При

ax 



   

 

1)()()()( OaxaxOaxOax

qpqpqp 





     

),min(

)()()(

qpqp

axOaxOaxO 



   

 

1)()()()( oaxaxoaxoax

qpqpqp 





     

),min(

)()()(

qpqp

axoaxoaxo 

При

|| x



   

 

1OxxOxOx

qpqpqp 





     

),max( qpqp

xOxOxO 



 

xOxO /1



Понятие степенного порядка малости и степенного порядка роста можно обобщить и на

случай дробных и произвольных показателей. При таком обобщении необходимо лишь

следить, чтобы переменная не вышла за границы области определения рассматриваемой

функции. Такие обобщения будут рассмотрены при рассмотрении конкретных функций.

Производная, первообразная и неопределенный интеграл

Дифференцируемые функции, производные и первообразные

Как показано выше, в окрестности точки непрерывности функция представляется в виде

суммы константы и бесконечно малой функции