Алексеев Д.В. Конспекты по общему курсу математики
Подождите немного. Документ загружается.


Сведения из элементарной математики 2
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Между любой парой рациональных чисел располагается бесконечное множество ве-
щественных чисел
Между любой парой иррациональных чисел находится хотя бы одно рациональное
число
Правила выполнения арифметических операций над вещественными числами ничем не
отличаются от соответствующих правил для рациональных чисел.
Между множеством вещественных чисел и точками прямой линии можно установить
взаимно однозначное соответствие (отсюда идет понятие «числовая прямая»).
Степени и логарифмы
Сводка правил действия со степенями
Степень с натуральным показателем определяется формулой
n
n
aaaa
.
Основной формулой алгебры степеней с натуральными показателями является следующие
из приведенного определения правила сложения показателей при перемножении степеней
mn
mn
mn
aaaaaaaaa
,
правило перемножения показателей при возведении степени в степень
mn
m
nnn
mn
aaaaaaaaaaa
)(
,
и правило перемножения степеней с одинаковыми показателями
n
n
nn
nn
bababababbbaaaba )()()()(
Вся дальнейшая алгебра степеней строится на основе сохранения справедливости этих ос-
новных правила для других показателей степени: целых, рациональных, вещественных.
Обобщение приведенных правил на случай когда показатели степени являются целыми
числами, осуществляется при помощи представления операции деления при помощи по-
казателя «минус единица»
0,/1
1
aaa
.
Из этого представления сразу следуют правила
1
01
aaa
,
nnnn
aaaa /1)()(
11
.
mnmn
aaa
/
,
nnnnn
bababa
/)/(
.
Дальнейшее обобщение правил действия со степенями на случай рациональных показате-
лей степени связано с определением корня действительного числа.
aa
n
n
.
Согласование данного определения с правилом перемножения показателей при возведе-
нии степени в степень, приводит к записи корня при помощи дробного показателя
n
n
aa
/1
.

Сведения из элементарной математики 3
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
В результате степень с рациональным показателем может быть представлена двумя спо-
собами
m
n
n
mnm
aaa
/
.
Если
0a
, то данная формула не приводит к противоречиям при любых значениях зна-
менателя и числителя показателя степени
mn,
. Если
0a
, то формула непротиворечива
только при нечетном знаменателе
12 kn
показателя степени, так как нельзя опреде-
лить корень четной степени из отрицательного числа.
1
Правила перемножения степеней и возведения степени в степень также справедливы и для
произвольных действительных показателей степени при выполнении условия
0a
. По-
следнее ограничение обусловлено тем, что определение степени с произвольным показа-
телем опирается на понятие логарифма и логарифмической функции.
Логарифмы и их основные свойства
Логарифм числа
b
по основанию
1a
, обозначаемый символом
)(log b
a
, - это показатель
степени, связывающий два положительных числа
ba,
)(log b
a
ab
.
Эта формула называется основным логарифмическим тождеством.
Определение логарифма и правила действия со степенями непосредственно приводят к
следующим свойствам логарифмов
)(log)(log)(log cbcb
aaa
,
)(log)(log bdb
a
d
a
.
Подставляя в эти формулы
1
fc
, и
0d
получаем,
)(log)(log)/(log fbfb
aaa
,
0)1(log
a
.
Для доказательства этих свойств надо просто записать рассматриваемые числа при помо-
щи основного логарифмического тождества и сравнить показатели степени. Например,
)(log)(log)(log)(log)(log
,,
cbcbcb
aaaaa
acbaacab
.
Важным следствием формулы для логарифма степени является формула связи логариф-
мов с различными основаниями
)(log)(log)(log)(log
)(log c
aaba
b
bbcc
.
Из этой формулы при
ac
следует, что
1)(log)(log)(log aba
aab
, то есть
)(log/1)(log ab
ba
.
Приведенных свойств логарифмов достаточно для выполнения различных тождественных
преобразований выражений, содержащих логарифмы.
Формулы сокращенного умножения
Бином Ньютона и его частные случаи
Биномом Ньютона с натуральным показателем называется многочлен
nn
n
nn
n
n
n
n
n
n
n
n
bCabCbaCbaCaCba
1222110
)(
.
1
Определение корня четной степени из отрицательного числа приводит к так называемым комплексным
числам, которые обобщают понятие вещественных чисел.

Сведения из элементарной математики 4
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Коэффициенты бинома Ньютона
k
n
C
называют биноминальными коэффициентами.
Биноминальные коэффициенты проще всего вычислить при помощи рассмотрения сле-
дующего частного случая бинома Ньютона
nn
n
nn
nnnn
n
xCxCxCxCCx
12210
)1(
.
Идея нахождения формул для биноминальных коэффициентов основана на вычислении
производных бинома в точке
0x
.
Дифференцируя обе части последнего равенства
k
раз при помощи правила дифференци-
рования степени
1
)(
mm
zmz
, и подставляя в полученную формулу
0x
, получаем
k
n
Ckkkknnnn 1)2)(1()1()2)(1(
,
то есть биноминальные коэффициенты выражаются через произведения последователь-
ных натуральных чисел
1)2)(1(
)1()2)(1(
kkk
knnnn
C
k
n
.
Для более удобной и компактной записи формул для биноминальных коэффициентов ис-
пользуют специальную функцию, обозначаемую символом
!x
и называемую факториал
(читается «икс-факториал»).
Если
nx
натуральное число, то факториал определяется формулой
nnn )1(321!
,
то есть факториал натурального числа равен произведению последовательных натураль-
ных чисел от единицы до аргумента факториала.
Факториал определяют также при помощи рекурсии, - процедуры определения функции
при последующем значении аргумента путем обращения к определению той же функции
при предыдущем значении аргумента. Для факториала такое определение имеет вид
!)1()!1( nnn
.
Формулы такого типа называются рекуррентными формулами
Чтобы рекуррентную формулу можно было использовать для вычислений ее необходимо
дополнить определением начального значения функции. Для функции факториал исполь-
зуют начальное значение
1!0
.
2
Умножив числитель и знаменатель определения
k
n
C
на произведение
12)1)(( knkn
, то есть на
)!( kn
факториал, запишем биноминальные коэффици-
енты в симметричном виде
)!(!
!
knk
n
C
k
n
.
Отсюда следует свойство симметрии биноминальных коэффициентов
2
Это определение начального значения связано с определением факториала как частного случая гамма
функции Эйлера
0
! dxexn
xn
.
Этот интеграл равен единице как при
0n
, так и при
1n
.

Сведения из элементарной математики 5
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
kn
n
k
n
C
knk
n
C
)!(!
!
.
Рассмотрим формулы бинома при двух последовательных значениях показателя степени
11
11
22
1
1
1
0
1
1
)1(
nn
n
nn
nnnn
n
xCxCxCxCCx
.
Ясно, что
)1)(()1(
122101
xxCxCxCxCCx
nn
n
nn
nnnn
n
.
Сравнивая коэффициенты при одинаковых степенях переменной в обеих формулах, полу-
чаем следующее рекуррентное соотношение
k
n
k
n
k
n
CCC
1
1
.
Данное соотношение удобно изобразить таблицей, называемой треугольником Паскаля.
Построение треугольника Паскаля осуществляется построчным выписыванием биноми-
нальных коэффициентов по нарастанию порядка бинома
n
0
n
C
1
n
C
2
n
C
3
n
C
4
n
C
5
n
C
6
n
C
7
n
C
8
n
C
0
1
1
1
1
2
1
2
1
3
1
3
3
1
4
1
4
6
4
1
5
1
5
10
10
5
1
6
1
6
15
20
15
6
1
7
1
7
21
35
35
21
7
1
8
1
8
28
56
70
56
28
8
1
Используя треугольник Паскаля, легко выписать частные случаи бинома Ньютона для
значений
3,2n
222
2)( bababa
,
32233
33)( babbaaba
.
Эти формулы известны как формулы сокращенного умножения «квадрат суммы» и «куб
суммы». Формулы сокращенного умножения называемые «квадрат разности» и «куб раз-
ности» получаются из них путем замены
bb
222
2)( bababa
,
32233
33)( babbaaba
.
Геометрическая прогрессия, ее частные случаи и
арифметическая прогрессия.
Геометрической прогрессией длины
n
называется последовательность чисел
122
,,,,,
nn
qpqpqpqpp
.
Число
1q
называется знаменателем геометрической прогрессии. При
0q
геометриче-
ская прогрессия называются знакопостоянной, а при
0q
, - знакопеременной.

Сведения из элементарной математики 6
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Геометрическую прогрессию можно также задать рекуррентной формулой
1,,
01
nkpppqp
kk
.
Нашей задачей будет вычисление суммы геометрической прогрессии
12
n
n
qpqpqppS
.
Для проведения суммирования умножим обе части этого равенства на
)1( q
, и запишем
результат в виде
).1(
)1(
12
12
nnn
n
n
qpqpqpqpqp
qpqpqppqS
Отсюда сразу следует формула суммы геометрической прогрессии
q
q
pS
n
n
1
1
.
Формула суммы геометрической прогрессии, записанная в виде
)1()1)(1(
12 nn
qpqqqqp
,
имеет прямое отношение к формулам сокращенного умножения известным как «разность
кубов» и «разность квадратов»
Положим в этой формуле
abqap
n
/,
. Тогда
nnnnnnn
bababbabaaba
))((
122321
.
При
3n
эта формула дает
3322
))(( babababa
,
а при
2n
22
))(( bababa
.
Особо отметим поведение этих формул при замене переменной
bb
. Формула «раз-
ность кубов» переходит в формулу «сумма кубов»
3322
))(( babababa
,
тогда как формула «разность квадратов» остается при такой замене неизменной, (форму-
лы «сумма квадратов» не существует!).
Обобщая сказанное можно утверждать, что разложение суммы геометрической прогрес-
сии на множители порождает формулы сокращенного умножения для разности и суммы
нечетных степеней, и для разности четных степеней.
Еще одним важным частным случаем геометрической прогрессии является бесконечная
геометрическая прогрессия
,,,,,,
122
nn
qpqpqpqpp
Для бесконечной геометрической прогрессии самым важным является вопрос о существо-
вании ее суммы.
Сумму бесконечной геометрической прогрессии определяют при помощи следующей
процедуры предельного перехода. При фиксированных значениях
qp,
вычисляют суммы

Сведения из элементарной математики 7
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
геометрических прогрессий различной длины
n
и затем отслеживают поведение этих
сумм при неограниченном увеличении
n
.
Получаемое при помощи такой процедуры значение суммы обозначают символом
n
n
Slim
.
Обозначение
)(lim nF
n
читается «предел
)(nF
при
n
».
Выделяя из формулы суммы геометрической прогрессии постоянное слагаемое, формулу
суммы бесконечной геометрической прогрессии можно записать в виде
)lim1(
1
lim
n
n
n
n
q
q
p
S
.
Отсюда видно, что вопрос о существовании суммы бесконечной геометрической прогрес-
сии определяется предельным поведением значений степенной функции
n
q
при
n
.
Когда
1|| q
, значения
n
q
стремятся к нулю (
0lim
n
n
q
) и сумма
q
p
S
1
.
Если
1q
, то
n
q
неограниченно растет с ростом
n
, (
n
n
qlim
). Если же
1q
, то
n
q
не принимает определенного значения при
n
(в таких случаях говорят, что предел не
существует). Следовательно, для значений
1|| q
сумма бесконечной геометрической
прогрессии не существует.
В заключении приведем рекуррентную формулу
1,,
01
nkaadaa
kk
,
которая определяет арифметическую прогрессию
3
dnadnadadaa )1(,)2(,,2,,
.
Для вычисления суммы арифметической прогрессии
n
A
заметим, что суммы пар слагае-
мых, равноотстоящих от концов арифметической прогрессии равны. Тогда для удвоенной
суммы можно записать
.)())2(())1((
))1(())2(()(2
adadnadna
dnadnadaaA
n
отсюда следует, что сумма
арифметической прогрессии
2
))1(2(
n
dnaA
n
.
Тригонометрия
Основные тригонометрические функции
При первом ознакомлении тригонометрия представляется нагромождением формул, кото-
рые невозможно запомнить. На самом деле для свободного владения тригонометрически-
ми функциями запоминать надо не так уж много. Это определение основных тригономет-
3
Существует простая связь между геометрической и арифметической прогрессиями. Если прологарифмиро-
вать члены геометрической прогрессии
)ln()ln()ln( qkpqp
k
, и обозначить
ap )ln(
,
dq )ln(
,
то мы придем к арифметической прогрессии.

Сведения из элементарной математики 8
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
рических функций, косинуса и синуса, и связанное с этим определением основное триго-
нометрическое тождество, а также формулы сложения для синуса и косинуса. Все ос-
тальное можно получить из этой тройки формул. В настоящем разделе будет показано, как
это можно сделать. При этом мы не будем воспроизводить все формулы тригонометрии, а
сконцентрируемся на демонстрации того, как работают при получении разнообразных то-
ждеств упомянутые выше три формулы.
Наиболее естественным определением тригонометрических функций является их геомет-
рическое определение как декартовых координат точки, расположенной на окружности
единичного радиуса с центром в начале координат, называемой тригонометрической ок-
ружностью.
Для задания положения точки на этой окружности используют следующее правило. По-
ложение точки задается при помощи угла, отсчитываемого от положительного направле-
ния оси абсцисс. Угол считается положительным, если направление поворота от оси абс-
цисс до рассматриваемой точки осуществляется против хода часовой стрелки. Угол счи-
тается отрицательным для поворота по ходу часовой стрелки.
Для измерения угла используется безразмерное, отношение длины дуги окружности к ее
радиусу, а угол, соответствующий длине дуги равной радиусу носит название один ради-
ан. Так как длина окружности равна
R
2
, то обход полной окружности соответствует из-
менению угла на
2
радиан.
Основные тригонометрические функции, косинус и синус, - это декартовы координаты
точки на тригонометрической окружности, положение которой задается углом
)sin()(),cos()(
yx
.
Непосредственно из этого определения получаются следующие свойства основных триго-
нометрических функций.
Периодичность. Поскольку изменение угла на
2
не меняет положения точки на триго-
нометрической окружности, косинус и синус являются периодическими функциями с пе-
риодом
2
:
,2,1),sin()2sin(),cos()2cos( nnn
Четность. Так как поворот от положительного направления оси абсцисс на одинаковые
по модулю, но разные по знаку углы приводит в точки, симметричные относительно оси
абсцисс, косинус является функцией четной, а синус, - нечетной
)sin()sin(),cos()cos(
.
Основное тригонометрическое тождество. Так как сумма квадратов координат точки на
тригонометрической окружности равна квадрату радиуса
1
22
yx
(теорема Пифагора),
косинус и синус удовлетворяют уравнению связи
1)(sin)(cos
22
.
Частные значения основных тригонометрических функций. Непосредственное считыва-
ние координат точек дает следующие значения тригонометрических функций углов, крат-
ных
2/
0
2/
2/3
)cos(
1
0
-1
0
)sin(
0
1
0
-1
Сведения из элементарной математики 9
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
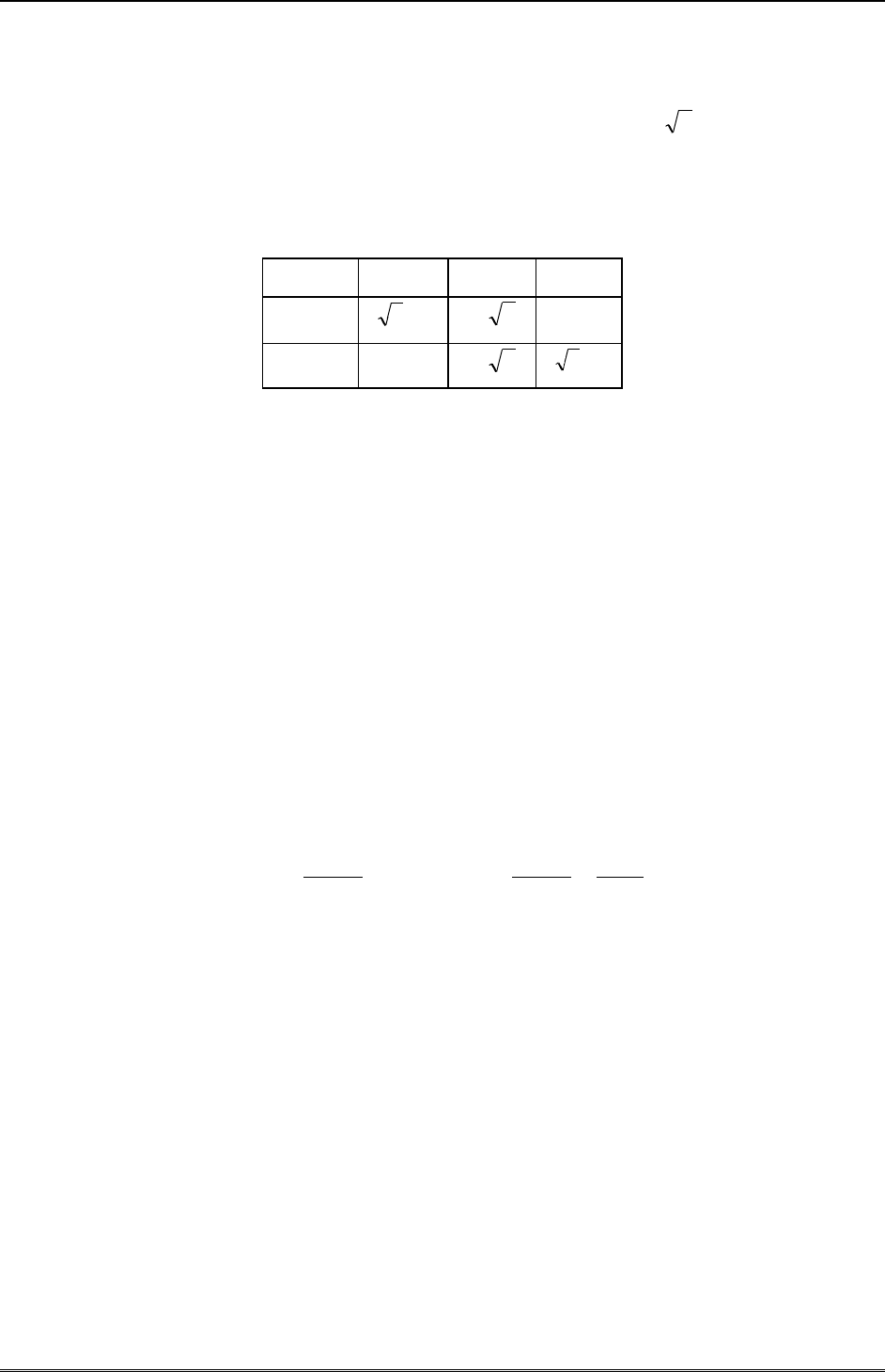
Полезно также запомнить значения тригонометрических функций углов
4/,3/,6/
.
Это легко сделать, связав при помощи двух прямоугольных треугольников, длина гипоте-
нузы которых равна единице.
С углом
4/
связан треугольник, длины катетов которого равны
2/1
. С углами
3/,6/
связан треугольник, у которого длина катета, расположенного напротив угла
6/
равна
2/1
. Наложите катет на ось абсцисс, вершину острого угла поместите в центр
тригонометрической окружности, и прочитайте значения косинуса и синуса используя
теорему Пифагора.
6/
4/
3/
)cos(
2/3
2/1
1/2
)sin(
1/2
2/1
2/3
Формулы сложения и их следствия
Формулы сложения для основных тригонометрических функций имеют вид
)sin()sin()cos()cos()cos( yxyxyx
)sin()cos()cos()sin()sin( yxyxyx
Эти формулы лучше запомнить, так как их вывод достаточно сложен, а сами формулы
просты.
Непосредственно из формул сложения следуют формулы для тригонометрических функ-
ций двойных углов, формулы приведения, формулы функций разности углов и формулы
представления суммы функций в виде произведения. Для лучшего усвоения этих следст-
вий, рекомендуется проводить их вывод самостоятельно, по ходу решения разных задач.
Другие тригонометрические функции
Остальные тригонометрические функции определяются через синус и косинус при помо-
щи арифметических операций. Так тангенс и котангенс определяются формулами
)cos(
)sin(
)tg(
x
x
x
,
)tg(
1
)sin(
)cos(
)ctg(
xx
x
x
.
Все свойства тангенса и котангенса (включая формулы сложения) получаются из основ-
ных свойств синуса и косинуса (смотри упражнения в конце раздела).
Обратные тригонометрические функции
Обратные тригонометрические функции выражают угол по значению тригонометрической
функции. В силу периодичности тригонометрических функций обратные тригонометри-
ческие функции являются многозначными, - одному значению тригонометрической функ-
ции соответствует бесконечное множество углов, отличающихся на период тригономет-
рической функции. Поэтому при работе с обратными тригонометрическими функциями
специально выделяют их главные значения, или однозначные ветви. По договоренности
главными значениями обратных тригонометрических функций являются
]2/;2/[),arcsin(
yxy
при
]1;1[x
];0[),arccos(
yxy
при
]1;1[x
)2/;2/(),arctg(
yxy
при
);( x

Сведения из элементарной математики 10
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
);0(),arcctg(
yxy
при
);( x
Поэтому, для обратных тригонометрических функций справедливы пары тождеств вида
xx ))(sin(arcsin
,
]2/;2/[,))(arcsin(sin
xxx
,
а, в общем случае,
xx ))(arcsin(sin
.
Линейная функция и квадратичная функция
Линейная функция и связанные с ней уравнения
и неравенства
Линейная функция, определяемая формулой
0, kbkxy
,
является простейшим примером функции.
Графиком линейной функции является прямая линия, проходящая через точки
)0;/(),;0( kbb
, расположенные на осях координат.
Параметрами линейной функции являются коэффициент наклона графика
12
12
)()(
xx
xyxy
x
y
k
,
и отрезок
)0(yb
, отсекаемый графиком на оси ординат.
Коэффициент наклона равен тангенсу угла между графиком и осью абсцисс, при условии,
что отсчет угла проводится по следующему стандартному правилу: угол, отсчитываемый
против хода часовой стрелки, считается положительным, а по ходу часовой стрелки, - от-
рицательным. Коэффициент наклона также равен производной линейной функции.
По знаку коэффициента наклона, линейные функции разделяются на два качественно раз-
личных класса, - возрастающие
)0( k
и убывающие
)0( k
.
Абсцисса точки пересечения графика с осью абсцисс, является решением уравнения
kbxbkxxy /,0,0)(
.
По графику также легко определить интервалы числовой оси, на которых линейная функ-
ция имеет постоянный знак. Так возрастающая линейная функция
0y
при
);/( kbx
и
0y
при
)/;( kbx
, а убывающая линейная функция
0y
при
)/;( kbx
и
0y
при
);/( kbx
.
Линейная функция может быть также представлена и более общим уравнением
0,0, bacbyax
.
В вырожденных случаях,
0a
или
0b
это уравнение описывает прямые линии, парал-
лельные координатным осям.
Система линейных уравнений с двумя неизвестными
Система линейных уравнений с двумя неизвестными
,
,
222
111
cybxa
cybxa
имеет следующую простую геометрическую интерпретацию. Каждое уравнение системы
определяет линейную функцию, или на языке графика - прямую линию. Решение рассмат-

Сведения из элементарной математики 11
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
риваемой системы, - это координаты точек (или сами точки) плоскости, принадлежащие
обоим прямым одновременно.
Для прямых линий, определяемых уравнениями рассматриваемой системы возможны сле-
дующие варианты.
1. Оба уравнения определяют одну и ту же прямую. В этом случае система имеет беско-
нечное множество решений, так как одно уравнение системы получается из другого
умножением на некоторое число. Аналитически это записывается в виде
1
2
1
2
1
2
121212
,,,
c
c
b
b
a
a
ccbbaa
.
2. Прямые параллельны. В этом случае система решений не имеет. Параллельность пря-
мых означает равенство коэффициентов наклона и неравенство отрезков, отсекаемых
на оси ординат. Аналитически это записывается в виде
1
2
1
2
1
2
22112211
,//,//
c
c
b
b
a
a
bcbcbaba
.
3. Прямые пресекаются. В этом случае система имеет единственное решение. Пересе-
кающиеся прямые имеют разные коэффициенты наклона, что записывается в виде
1
2
1
2
2211
,//
b
b
a
a
baba
.
При необходимости, соответствующие графические иллюстрации нетрудно построить в
каждом конкретном случая.
Перечисленные результаты сами по себе достаточно просты, но они находят применение
и в разнообразных «нестандартных» задачах, сводящихся к исследованию систем линей-
ных уравнений.
Квадратичная функция
Квадратичная функция, или квадратный трехчлен, является одним из наиболее распро-
страненных мотивов экзаменационных задач. Когда говорят, что в школе не решают задач
с параметрами, довольно сильно лукавят. Исследование квадратного трехчлена, - это за-
дача с тремя параметрами.
Как сказано в одном из популярных пособий по подготовке к экзаменам: «Маленькое бе-
лое пятнышко в теме «Квадратный трехчлен» приведет к появлению огромных мертвых
зон в знаниях элементарной математики».
Квадратичной функцией, или квадратным трехчленом, называется функция, задаваемая
формулой
cbxaxy
2
.
В этой формуле обязательно должно выполнятся условие
0a
, иначе функция станет ли-
нейной.
Главным свойством квадратичной функции является то, что ее качественное поведение
полностью контролируется двумя параметрами, - дискриминантом
acbD 4
2
и знаком
коэффициента при старшей степени переменной
a
.
Существует только шесть качественно различных видов квадратичной функции, которые
классифицируются по коэффициенту при старшей степени и дискриминанту, следующим
образом.
