Алексеев Д.В. Конспекты по общему курсу математики

Подождите немного. Документ загружается.

Основные элементарные функции (справочные сведения и примеры исследования)

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Пример 36.





 x

y ,

. При больших значениях переменной числитель и зна-

менатель являются бесконечно большими функциями третьего порядка, то есть функция

имеет неопределенность

/

. Преобразуем формулу функции вынесением старшей сте-

пени за скобку

 

113

4/5)4/11)(5/11(

)4/11(4

)5/11(5











 xOxx

Следовательно, при больших значениях аргумента функция является ограниченной, то

есть имеет горизонтальную асимптоту.

Пример 37.

 xxxy ),/21ln(

. Функция имеет неопределенность

0

. Восполь-

зуемся разложением Маклорена для логарифма по переменной

z x 2

2264243244

/82)/8/2/2()3/2/()1ln( xxxxxxzzzxzxy







Отсюда видно, что при

x  

функция является бесконечно большой второго порядка, а

ее график приближается к параболе

 xy

сверху.

Неопределенности



Пример 38.

 xxxxxy ,29

. Преобразуем формулу функции вынося

старшую степень из под знака радикала и используем разложение бинома

xxxxxxxxxxxxy

/||3||)/11(||)/31()/21(||)/91(

2/13/1







Следовательно, при

x  

функция является ограниченной (имеет горизонтальную

асимптоту

y  2

), а при

x  

, - бесконечно большой первого порядка (имеет наклон-

ную асимптоту

y x 2 4

Пример 39.

 xxxxxxy ,0),ln()ln(

. В окрестности обоих точек

функция имеет неопределенность

  

. Для раскрытия неопределенностей преобразуем

функцию при помощи свойств логарифмов и воспользуемся разложением Маклорена для

логарифма

xxxxxxxxxy





)1ln()1ln())1(ln())1(ln(

)ln()/11ln()/11ln()ln())/11(ln())/11(ln(

2232

xxxxxxxxy





то есть при

x  0

функция является бесконечно малой первого порядка, а при

x  

- бесконечно большой с логарифмическим ростом.

Неопределенности

,1 ,0 



Пример 40.

0,)1(

 xaxy

. Функция имеет неопределенность



. Преобразуем

сложную показательную функцию к постоянному основанию при помощи замены

))1exp(ln(1 axax 

и раскроем неопределенность в показателе при помощи разложения

Маклорена для логарифма

exbaba

xaaxb

axb

)2/exp(

)2/(

exp

)1ln(

exp



































 



Основные элементарные функции (справочные сведения и примеры исследования)

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

то есть при

0x

функция ограниченная.

Пример 41.

 xxy

. Функция имеет неопределенность



. Преобразуем слож-

ную показательную функцию заменой переменной

 zzx ),exp(

1/1)/exp()/)exp(ln( 



ezezxxy

, то есть при

x

функция является огра-

ниченной (имеет горизонтальную асимптоту

1y

Пример 42.



 0, xxy

. Функция имеет неопределенность

. Преобразуем показа-

тельную функцию заменой

 zzx ),exp(

11)exp())ln(exp( 



zezexxy

то есть при



 0x

функция ограниченная.

Пример 43.



 0),ln()1( xxxy

. Функция содержит несколько неопределенностей.

Для их раскрытия сделаем замену

 zzx ),exp(

и преобразуем показательную

функцию к постоянному основанию

)exp()1)(exp()ln()1))ln((exp(

zzzzexxxy





то есть при



 0x

является экспоненциальной бесконечно малой.

Построение графиков функций

В настоящем разделе будет показано, как исследование функции вблизи нулей, точек раз-

рыва и при больших значениях аргумента сливаются в единое исследование поведения

функции на всей области определения. Последовательность действий при таком исследо-

вании примерно следующая.

 Находим область определения функции.

 Находим нули функции и определяем порядок малости функции вблизи нулей.

 Исследуем поведение функции в окрестности точек разрыва.

 Исследуем поведение функции при больших значениях переменной.

 По полученной выше информации строим схему графика функции

 Уточняем положение экстремумов и точек перегиба графика, используя производ-

ные первого и второго порядка.

Как видно из перечисленных пунктов исследования функции, основная работа проводить-

ся с формулой функции, а производные привлекаются лишь для уточнения деталей. Рас-

сматриваемые ниже примеры призваны показать, что применять изложенную схему надо

не догматически, а с учетом конкретной формулы функции.

Пример 44.

 xxy

. Исследуемая функция многочлен. Разлагаем его в произведе-

ние элементарных сомножителей

)2()1()1(2)1)(1()1(2

 xxxxxxxxxy

Отсюда видно, что рассматриваемый многочлен имеет нуль первого порядка при

2x

нуль второго порядка при

1x

Выписываем приближенные формулы, описывающие поведение многочлена вблизи его

нулей и при больших значениях аргумента

,)1(3),2(9 xyxyxy

xxx 



Отсюда видно, что график пересекает ось абсцисс при

x  2

меняя знак с отрицательно-

го на положительный и касается оси абсцисс сверху в точке

x  1

Частные случаи полученной формулы

eNx





)/11(lim)1(lim

называют вторым замечатель-

ным пределом.

Основные элементарные функции (справочные сведения и примеры исследования)

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Непрерывность графика требует наличия локального максимума на интервале

( ; )2 1

. Для

уточнения его положения находим нули производной

)1)(1(3)1(3





xxxy

. Нуль

производной

1x

соответствует локальному минимуму функции - касанию графиком оси

абсцисс, а нуль

1x

- искомому локальному максимуму

max

y

Пример 45.

)2/()1)(1(  xxxy

. Исследуемая рациональная дробь имеет нуль перво-

го порядка в точке

1x

, нуль второго порядка с точке

1x

и точку разрыва

2x

Приближенные формулы, описывающие поведение исследуемой функции вблизи нулей и

разрыва имеют вид:

)2/(3,)1(2),1)(9/4( 



xyxyxy

xxx

Следовательно, исследуемая функция является бесконечно малой первого порядка в окре-

стности

x  1

, положительной бесконечно малой второго порядка в окрестности

x  1

положительной бесконечно большой в окрестности вертикальной асимптоты

x  2

Так как старшая степень числителя на единицу больше старшей степени знаменателя, ис-

следуемая функция имеет наклонную асимптоту, уравнение которой проще получить раз-

ложением по степеням

xz /1

3)/41)(/21)(/11()/21()/11)(/11(







xxxxxxxxxy

Суммируя полученные результаты на схеме графика, получаем, что функция должна

иметь локальный максимум на интервале

( ; )11

и локальный минимум при

x  2

. Для

уточнения положения локальных экстремумов находим нули производной

)2/()5)(1( 



xxxxy

Нулю производной

x  1

соответствует локальный минимум, являющейся нулем функ-

ции, искомый локальный минимум находится в точке

5x

, а локальный максимум, - в

точке

0x

. Вычисляем значения функции в точках экстремумов

4/1)0( y

3/32)5( y

уточняем график функции.

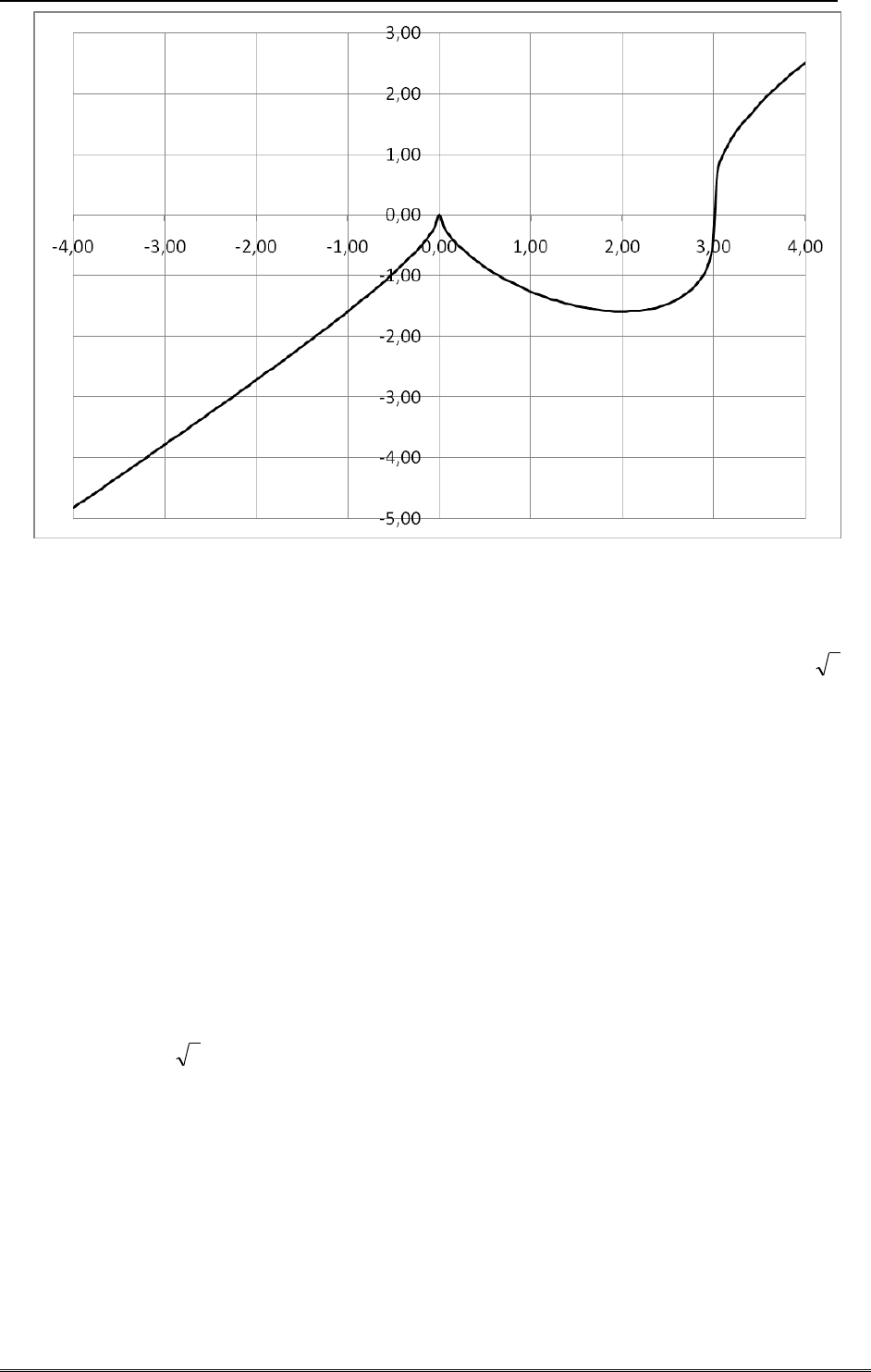
Пример 46.

3xxy 

. Функция определена при любых значениях переменной. Нули

функции находятся в точках

0x

3x

. Приближенные формулы, описывающие пове-

дение функции в окрестности ее нулей имеют вид:

3/1

3/2

3/13/2

9)3(,3)3( 



xyxxxy

Отсюда видно, что порядок малости исследуемой функции вблизи ее нулей описывается

дробными показателями степени. Вблизи

3x

функция меняет знак с отрицательного на

положительный, а вблизи

0x

является отрицательной бесконечно малой, то есть имеет

локальный максимум.

Поведение функции при больших значениях аргумента получаем при помощи разложения

по степеням

xz /1

1)1()31()/31(

3/13/1





xzzxzxxxy



, следовательно,

функция имеет наклонную асимптоту.

Из непрерывности функции и ее поведения в исследованных точках следует ожидать, что

функция должна иметь локальный минимум на интервале

( ; )0 3

. Для уточнения его поло-

жения находим нули производной

3/23/1

)3()2(3







xxxy

. Искомый минимум находит-

ся в точке

4)2(,2  yx

. На приведенном ниже рисунке график этой функции по-

строен с помощью Microsoft Excel.

Основные элементарные функции (справочные сведения и примеры исследования)

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Пример 47.

)/1exp()2( xxy 

. Функция имеет точку разрыва

0x

. Справа от точки

разрыва функция является положительной экспоненциальной малой, а слева, - положи-

тельной экспоненциальной большой:









0)/1exp(2,)/1exp(2

xyxy

При

2x

функция имеет нуль, и описывается приближенной формулой

exy

/)2(





то есть вблизи

2x

функция является бесконечно малой первого порядка и меняет знак с

отрицательного на положительный.

Приближенная формула, описывающая поведение функции при больших значениях пере-

менной получается разложением по степеням

xz /1

xzzxzxy





3)2/1)(2()exp()2(



Следовательно, график имеет наклонную асимптоту

xy  3

Из поведения функции на участках непрерывности следует ожидать наличия локального

минимума на при

0x

и локального максимума на интервале

)2;0(

.Для уточнения поло-

жений локальных экстремумов находим производную:

)/1exp()1)(2(

xxxxy 





Из нулей производной находим, что локальный минимум расположен в точке

eyx 4)2(,2 

, а локальный максимум, - в точке

eyx /1)1(,1 