Алексеев Д.В. Конспекты по общему курсу математики
Подождите немного. Документ загружается.


Основные элементарные функции (справочные сведения и примеры исследования)
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
13
1)2exp(
1)2exp(
)sh(
)ch(
)cth(,
1)2exp(
1)2exp(
)ch(
)sh(
)th(
x
x
x
x
x
x
x
x
x
x
.
Отсюда видно, что гиперболический тангенс определен при любых значениях перемен-
ной, а гиперболический котангенс – всюду, кроме
0x
. Обе функции являются нечетны-
ми и ограниченными при больших значениях переменной. Соответствующие предельные
формулы имеют вид:
1
1)2exp(
1)2exp(
lim)cth(lim,1
)2exp(1
)2exp(1
lim)th(lim
x
x
x
x
x
x
xxxx
.
В окрестности нуля гиперболический тангенс является бесконечно малой первого поряд-
ка, а гиперболический котангенс - бесконечно большой первого порядка (в этом легко
убедиться, разлагая экспоненту в ряд Маклорена)
x
x
x
xx
x
x
x
xx
/1
1)21(
1)21(
)cth(,
1)21(
1)21(
)th(
00
.
Формулы для производных гиперболического тангенса и гиперболического котангенса
получаются при помощи правила дифференцирования частного и формул для производ-
ных гиперболического синуса и гиперболического косинуса
)(/sh1))(cth(),(/ch1))(th(
22
xxxx
.
Соответствующие им формулы интегрирования выписываются без затруднения
Обратные гиперболические функции
Особенностью обратных гиперболических функций является то, что при помощи алгеб-
раических преобразований они могут быть выражены через натуральный логарифм. Про-
иллюстрируем эту процедуру на примере гиперболического синуса, который является
строго монотонной функцией и имеет обратную функцию на всей области определения.
Согласно определению обратной функции, обратный гиперболический синус
)Arsh(xu
является решением уравнения
2/))exp()(exp( uux
, которое заменой переменной
0)exp( uz
сводится к квадратному уравнению
012
2
xzz
. Формула для обратного
гиперболического синуса получается логарифмированием положительного решения по-
следнего уравнения:
)1ln()Arsh(
2
xxx
.
Аналогично находятся формулы и для других обратных гиперболических функций.
1||),1ln()Arch(
2
xxxx
,
1||)),1/()1ln(()2/1()Arth( xxxx
,
1||)),1/()1ln(()2/1()Arcth( xxxx
.
Непосредственно из этих формул следует логарифмический рост обратного гиперболиче-
ского синуса и обратного гиперболического косинуса при больших значениях перемен-
ной, а также логарифмический рост обратного гиперболического тангенса и обратного ги-
перболического котангенса вблизи границы области определения
|)|2/1ln()Arsh(,)2ln()Arsh( xxxx
xx
,
0)1(2)Arch(,)2ln()Arch(
1
xxxx
xx
,

Основные элементарные функции (справочные сведения и примеры исследования)
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
14
)2/)1ln(()2/1()Arth(,))1/(2ln()2/1()Arth(
11
xxxx
xx
,
)2/)1ln(()2/1()Arcth(,))1/(2ln()2/1()Arcth(
11
xxxx
xx
.
Выписанные приближенные формулы получены разложением функций находящихся под
знаком логарифма в ряд Тейлора.
Дифференцирование обратных гиперболических функций проводится при помощи прави-
ла дифференцирования сложной функции:
1/1)1())(ln())(Arsh(
22
xxxux
,
,1||),1/(1))1)(ln(2/1())1)(ln(2/1())(Arth(
2
xxxxx
1||),1/(1))((Arcth,1/1))(Arch(
22
xxxxx
.
Обращение формул дифференцирования дает интегральные представления для обратных
гиперболических функций:
xxx
dz
z
xdz
z
xdz
z
x
0
2
1
2
0
2
1
1
)Arth(,
1
1
)Arch(,
1
1
)Arsh(
.
Выписанные интегральные представления используются для получения рядов Маклорена
для обратных гиперболических функций:
53
0
32
0
2
)8/3()6/1())8/3()2/1(1(
1
1
)Arsh( xxxdzzzdz
z
x
xx
,
53
0
42
0
2
)5/1()3/1()1(
1
1
)Arth( xxxdzzzdz
z
x
xx
.
Формула Эйлера и связь тригонометрических и гиперболических функций
Тот факт, что формулы, описывающие свойства тригонометрических и гиперболических
функций очень похожи, не случаен. Он является следствием того факта, что тригономет-
рические функции, подобно гиперболическим функциям, могут быть выражены через по-
казательную функцию, но от мнимого аргумента
)exp(
i
.
Мнимые числа, - алгебраические объекты вида
yi
, являются частным случаем так назы-
ваемых комплексных чисел, - алгебраических объектов вида
yixz
, построенных при
помощи сложения и умножения из пары действительных чисел
yx,
и принципиально но-
вого алгебраического объекта, называемого мнимой единицей, которая удовлетворяет сле-
дующему непривычному условию
1
2
iii
.
Действия с комплексными числами можно проводить при помощи обычных алгебраиче-
ских правил, но с учетом нового правила умножения мнимой единицы, например:
iiiiii 83462)21()32(
2
.
Введение комплексных чисел позволяет определить квадратный корень из отрицательных
чисел
aia
2
, и как следствие этого найти корни квадратного уравнения и с отрица-
тельным дискриминантом
aDibzacbDcbzaz 2/)||( ,04 ,0
2,1
22
.

Основные элементарные функции (справочные сведения и примеры исследования)
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
15
В результате теорему о разложении многочленов в произведение элементарных сомножи-
телей можно переформулировать в виде: любой многочлен разлагается в произведение ли-
нейных сомножителей, число которых равно его степени.
Показательная функция с мнимым аргументом определяется при помощи разложения
стандартной экспоненты в ряд Маклорена
4
!5
)(
!4
)(
!3
)(
!2
)(
1)exp(
5432
iiii
ii
.
После возведения мнимой единицы в степень, все слагаемые данного ряда разбиваются на
два типа, - нечетные степени содержат мнимую единицу в качестве общего множителя, а
четные степени мнимой единицы не содержат. В результате группировка слагаемых дает
!5!3!4!2
1)exp(
5342
ii
.
Сравнение входящих в эту формулу рядов с рядами для синуса и косинуса и приводит к
формуле устанавливающей связь между экспонентой и тригонометрическими функциями,
которая и называется формулой Эйлера
)sin()cos()exp(
ii
.
Из формулы Эйлера при помощи простых вычислений получается связь между показа-
тельной функцией и тригонометрическими функциями
)sin()cos()exp(
ii
,
)sin()cos()sin()cos()exp(
iii
,
2/))exp()(exp()cos(
ii
,
iii 2/))exp()(exp()sin(
а также связь между гиперболическими и тригонометрическими функциями
)sh()sin( ),ch()cos( ),sin()sh( ),cos()ch(
iiiiii
.
Формула Эйлера позволяет очень просто, при помощи перемножения получить формулы
сложения для тригонометрических функций:
))(exp()exp()exp( yxiiyix
,
)sin()cos())sin()))(cos(sin()(cos( yxiyxyiyxix
,
)sin()cos())sin()cos()cos()(sin())sin()sin()cos()(cos( yxiyxyxyxiyxyx
.
Исследование бесконечно малых функций
Степенной порядок малости
Пусть функция имеет нуль в точке
ax
. Для определения порядка малости функции
вблизи этой точки надо разложить функцию в ряд Тейлора. Наименьший показатель сте-
пени приращения переменной
ax
в полученном разложении и есть искомый порядок
малости функции.
Пример 1.
3579
33 xxxxy
. Разлагаем многочлен в произведение элементарных со-
множителей
3333232463
)1()1()1()133( xxxxxxxxxy
.
4
Законность этого разложения основана на определении абсолютной сходимости степенных рядов. Не вда-
ваясь в подробности, укажем, что степенной ряд экспоненты сходится абсолютно при любом комплексном
значении переменной, в том числе, мнимом.
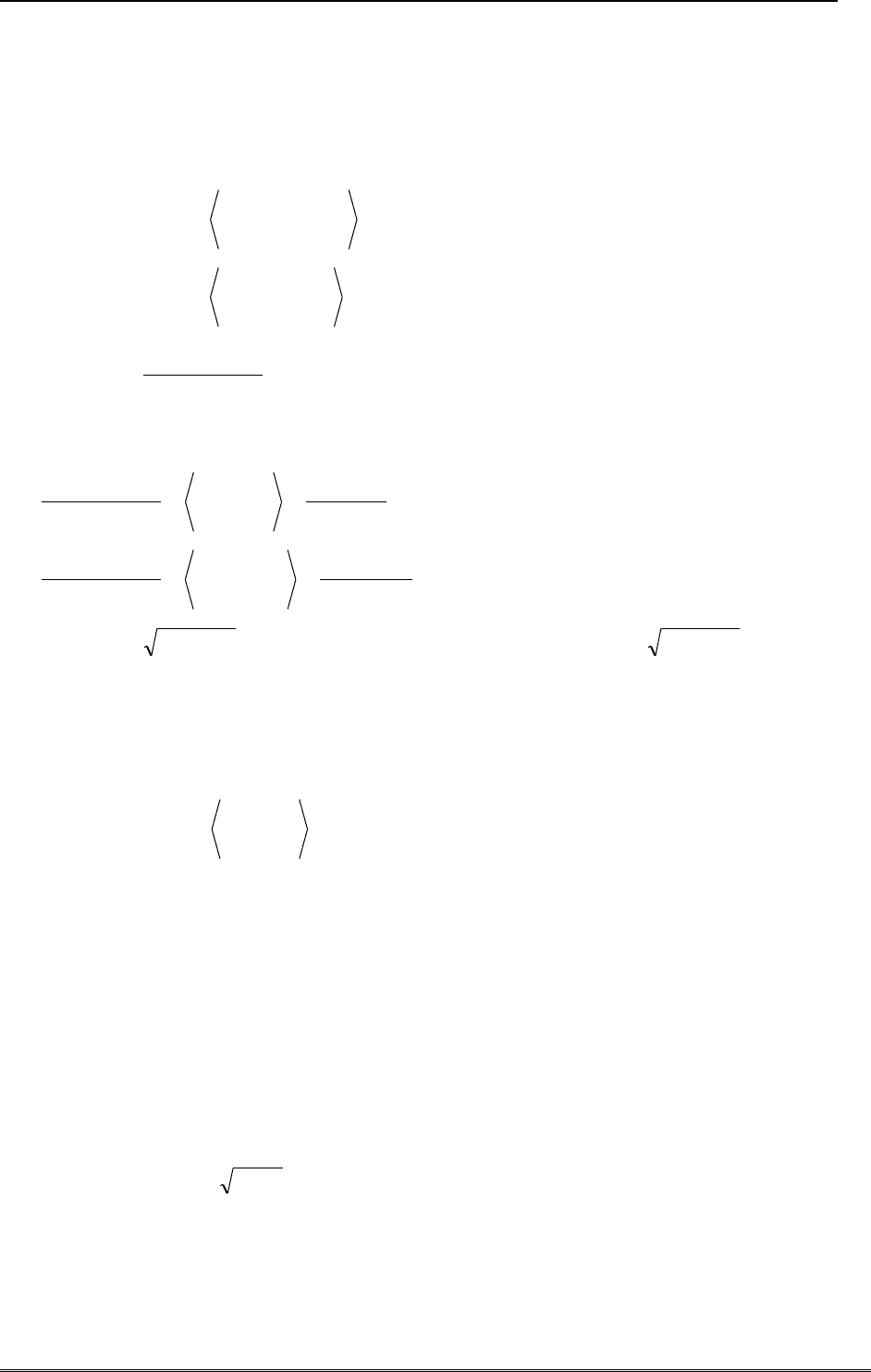
Основные элементарные функции (справочные сведения и примеры исследования)
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
16
Отсюда видно, что многочлен имеет нули третьего порядка в точках
1
1
x
,
0
2
x
,
1
3
x
. Согласно полученному выше результату о порядке нулей многочлена, рассматриваемый
многочлен в окрестности всех своих нулей является бесконечно малой третьего порядка, а
приближенные формулы имеют вид:
3
0
333
)1()1( xxxxy
x
,
33
0
333333
)1(88)2()1(
0,1
,1
)1()1(
xzzzz
zx
zx
xxxy
z
,
33
0
333333
)1(88)2()1(
0,1
,1
)1()1(
xzzzz
zx
zx
xxxy
z
Пример 2.
3
2
)2(
)1)(1(
x
xx
y
. Функция имеет нуль первого порядка в точке
x 1
и нуль
второго порядка в точке
x 1
. Искомые приближенные формулы получаем по описан-
ной в предыдущем примере схеме.
)1(44
)1(
)2(
0
,1
)2(
)1)(1(
0
3
2
3
2
xz
z
zz
z
zx
x
xx
y
z
,
22
0
3
2
3
2
)1(427/2
)3(
)2(
0
,1
)2(
)1)(1(
xz
z
zz
z
zx
x
xx
y
z
.
Пример 3.
xxxy
3
)12(
. Находим нули функции из уравнения
0)12(
3
xxx
.
Получаем
1,0,)1()12(,0)12(
21
223
xxxxxxxxxx
. Разложение функции
в ряд при помощи формулы бинома Ньютона с произвольным показателем дает:
3/13/23/1
0
3/23/13/1
)))3/2(1(())21(( xxxxxxxy
x
,
.3/)1(3/)1)9/43/21)(9/3/1(
)1()21()1(
0
,1
)12(
2222
0
3/13/13/13/1
xzzzzzz
zzz
z
zx
xxxy
z
Следовательно, порядок малости функции вблизи
x 1
равен двум, а вблизи
x 0
опи-
сывается дробным показателем степени 1/3.
В следующих примерах необходимо определить порядок малости функций вблизи ука-
занных точек.
Пример 4.
0),1ln()tg(
22
xxxy
. Полагая
0
2
zx
, получаем
3/3/)tg(
623
xxzzz
,
2/2/)1ln(
422
xxzzz
,
2/)2/()3/(
44262
0
xxxxxy
x
, то есть искомый порядок малости равен 4.
Пример 5.
0,1)cos(
2
xxxy
. Полагая под знаком корня
x z
2
и используя раз-
ложения Маклорена для косинуса и бинома, получаем
8/2/18/2/1)1(
4222/1
xxzzz
,
6/)8/2/1()24/2/1(
44242
0
xxxxxy
x
, то есть порядок малости равен 4.

Основные элементарные функции (справочные сведения и примеры исследования)
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
17
Пример 6.
0),sin(
2
xxxexy
x
. Перемножение степеней на разложения Маклорена
для экспоненты и синуса получаем
3322
0
)6/()2/1( xxxxxxxy
x
, то есть
порядок малости равен 3.
Пример 7.
1, xeey
x
. Делая замену
0,1 zzx
, получаем
)1()2/()1)(exp()1exp(
2
0
xeezzzezeezy
z
.
Пример 8.
3/,))3cos(1(
3
xxy
. Полагаем
3/
zx
, и используем формулу при-
ведения
632
3
2
0
33
)3/)(8/721())2/9((
2
)3(
11))3cos(1())3cos(1(
xz
z
zzy
z
,
То есть порядок малости равен 6.
Пример 9.
exxy )),(ln(ln
2
. Полагаем
0, zezx
. и преобразуем исходную
функцию при помощи свойств логарифмов
222
0
22
)1/()/())/1(ln())/1ln(1(ln)))/1((ln(ln
exezezezezey
z
, то есть поря-
док малости равен 2.
Замечания о функциях с нестепенным порядком малости
Может оказаться, что функция в окрестности исследуемой точки является бесконечно ма-
лой, но в самой точке не определена. В таких случаях невозможно разложить функцию в
ряд Тейлора и описать ее поведение степенными функциями. Для описания характера ма-
лости функций в точках такого типа часто используются логарифмы и экспоненты. Ниже
приводятся простые примеры функций с нестепенным порядком малости.
Экспоненциально малые функции
0|),|/1exp( xприxy
,
axприaxy ),)/(1exp(
4
,
xилиxприxy 0)),(lnexp(
2
.
Логарифмически малые функции
xилиxxy 0)),ln(/1
,
1)),ln(ln(/1 xилиxxy
.
Используя эти функции в качестве основы, читатель может самостоятельно построить
другие примеры функций с нестепенной малостью.
Исследование бесконечно больших функций
В простейшем случае бесконечно большая функция получается делением ограниченной
функции на бесконечно малую функцию.
5
В настоящем разделе рассматриваются приме-
ры нахождения порядка роста функций именно в этом простейшем случае. Примеры оп-
ределения порядка роста функций, содержащих неопределенности будут рассмотрены
ниже.
Степенной порядок роста
Пример 10.
22
3
)1(
x
x
y
. Вертикальные асимптоты функции определяются нулями знаме-
нателя, которые имеют второй порядок, то есть, в окрестности обеих асимптот функция
5
Говорят, что функция имеет разрыв второго рода в некоторой точке, если она вблизи этой точки является
бесконечно большой.
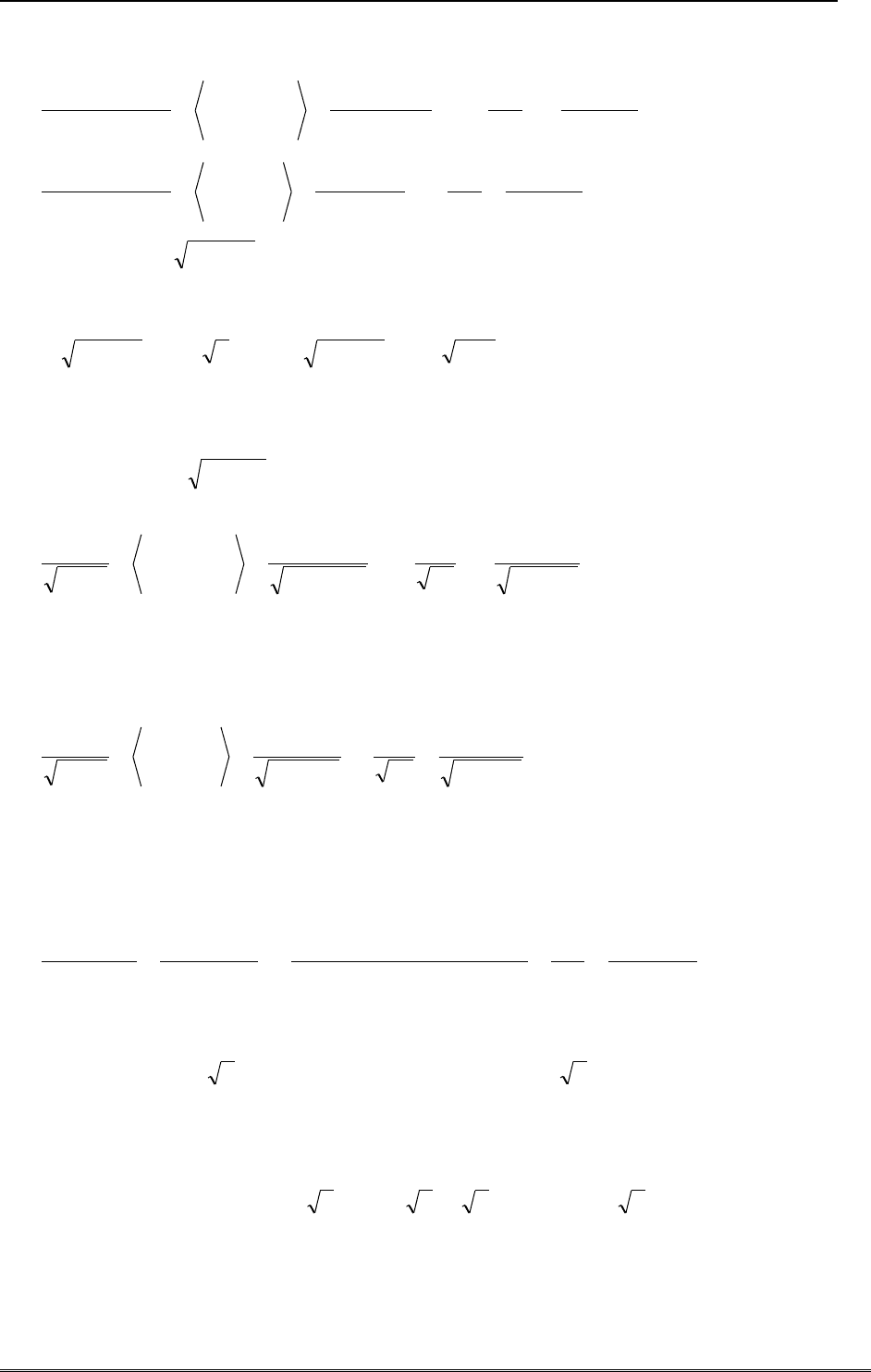
Основные элементарные функции (справочные сведения и примеры исследования)
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
18
является бесконечно большой второго порядка. Поведение функции в окрестности асим-
птот описывается приближенными формулами
22
0
2
22
3
22
3
)1(4
1
4
1
)2(
)1(
0
,1
)1()1(
xzzz
z
z
zx
xx
x
y
z
,
22
0
2
22
3
22
3
)1(4
1
4
1
)2(
)1(
0
,1
)1()1(
xzzz
z
z
zx
xx
x
y
z
.
Пример 11.
)1(/1 xxy
. Функция определена на открытом интервале
( ; )0 1
. Вблизи
границ области определения поведение функции описывается приближенными формула-
ми
xxxy
x
/1)1(/1
0
,
xxxy
x
1/1)1(/1
1
Следовательно, вблизи обеих границ области определения функция является положитель-
ной бесконечно большой порядка 1/2.
Пример 12.
3
22
)1(/ xxy
. Нули знаменателя
x 1
и
x 1
определяют положение то-
чек разрыва. Вблизи асимптоты
x 1
приближенная формула для функции имеет вид
3
3
0
3
2
3
2
2
)1(2
1
2
1
)2(
)1(
0
,1
1
xzzz
z
z
zx
x
x
y
z
,
то есть вблизи этой асимптоты функция является бесконечно большой порядка 1/3 поло-
жительной слева от асимптоты и отрицательной справа от асимптоты. Аналогично, вблизи
асимптоты
x 1
функция также является бесконечно большой порядка 1/3, но отрица-
тельной слева от асимптоты и положительной справа от асимптоты:
3
3
0
3
2
3
2
2
)1(2
1
2
1
)2(
)1(
0
,1
1
xzzz
z
z
zx
x
x
y
z
.
Пример 13.
))3cos(1/(2 xy
. Нули знаменателя
3/)12( nx
n
. Сделав замену пере-
менной
0, zzxx
n
, преобразуем формулу функции в окрестности точки разрыва
при помощи формул приведения и удвоения углов, и используем разложение Маклорена
для синуса
2223
0
2
)(9
4
9
4
)6/)2/3()2/3((
1
)2/3(sin
1
)3cos(1
2
n
z
xxzzzzz
y
,
то есть что в окрестности всех точек разрыва функция является положительной беско-
нечно большой второго порядка
Пример 14.
)sin(/1 xy
. Находим нули знаменателя
22
,0)sin( nxx
n
. Следо-
вательно, функция имеет вертикальные асимптоты в точках
x n
2 2
. При этом асимптота
x 0
является границей области определения функции. Вблизи границы области опреде-
ления поведение функции описывается приближенной формулой
xxxxy
x
/1)6/)(/(1)sin(/1
3
0
.
то есть функция является положительной бесконечно большой порядка 1/2. В окрестности
остальных асимптот преобразуем формулу функции при помощи замены переменной
0,
22
zznx
и разложений Маклорена для синуса и квадратного корня
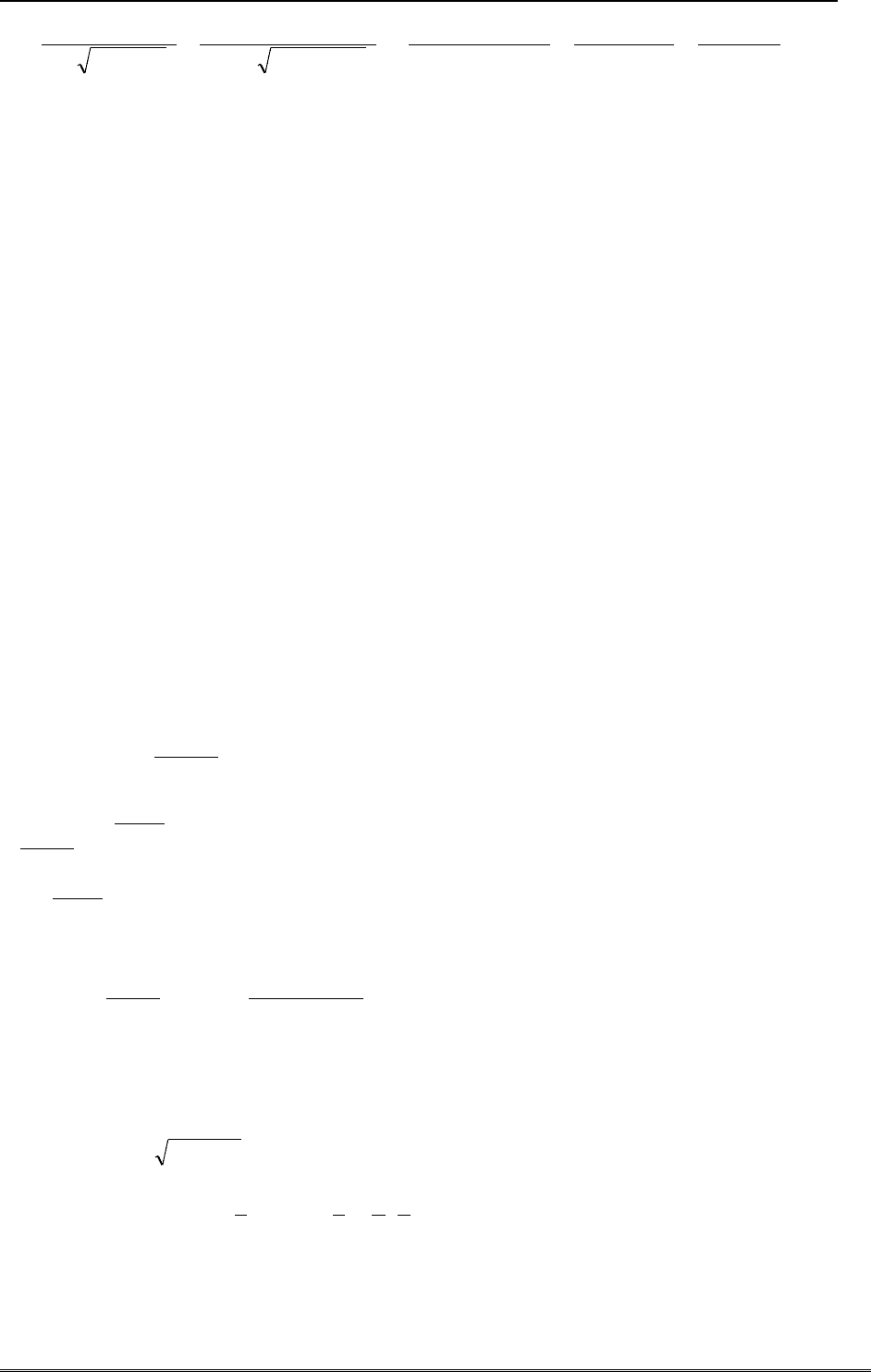
Основные элементарные функции (справочные сведения и примеры исследования)
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
19
22
0
2222
2)1(
)2/sin(
)1(
)2/sin(
1
)/1sin(
1
)sin(
1
nx
n
nznzn
nznzn
y
nn
z
,
то есть вблизи точек разрыва
x n
2 2
функция является бесконечно большой первого по-
рядка, а ее знак зависит от четности номера точки разрыва.
Замечание о функциях с нестепенным порядком роста
Примеры функций с нестепенным ростом можно получить непосредственно из приведен-
ных в предыдущем разделе функций с нестепенной малостью.
Функции с экспоненциальным ростом
0|),|/1exp( xxy
,
axaxy ),)/(1exp(
4
,
xилиxxy 0)),(exp(ln
2
.
Функции с логарифмическим ростом
xилиxxy 0)),ln(
,
1)),ln(ln( xилиxxy
.
Исследование функций при больших значениях переменной
Для исследования функции при больших значениях переменной необходимо написать со-
ответствующую приближенную формулу с требуемой точностью. Точность формулы оп-
ределяется характером решаемой задачи и может быть различной даже для одной и той же
функции. Приближенные формулы также определяются конкретной исследуемой функци-
ей, и их вид не ограничен каким либо конкретным классом функций. Отдельно выделяют
случай, когда при больших значениях аргумента функция ведет себя как линейная функ-
ция. (в таких случаях говорят, что график функции имеет наклонную асимптоту).
Наклонные асимптоты функций
Пример 15.
1
2
23
x
xx
y
. Выделяем целую часть дроби делением
_ |x x x
x x x
x x
x
x
3 2 2
3
2
2
1
1
1
1
_
и записываем исходную функцию в виде суммы целой части и правильной дроби
y x
x
x
x
x x
x x
x x
x
1
1
1
1
1 1
1 1
1 1
2 2 2
( / )
( / )
/
.
Функция имеет наклонную асимптоту
y x 1
, а знак бесконечно малой добавки указы-
вает, что при отрицательных значениях переменной график приближается к асимптоте
снизу, а при положительных значениях переменной, - сверху.
Пример 16.
3
23
3xxy
. Используем разложение бинома по переменной
z x 3 /
xxxxxxxy
x
/11)/3(
2
1
)
3
2
(
3
1
)/3(
3
1
1)/31(
23/1
.
График функции приближается к асимптоте
y x 1
сверху при
x
и снизу при
x
.

Основные элементарные функции (справочные сведения и примеры исследования)
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
20
Пример 17.
4
34
xxy
. Используем разложение бинома по переменной
z x 1 /
||32/34/||||))/1(
32
3
)/1(
4
1
1(||)/11(||
24/1
xxxxxxxxxy
x
.
Функция имеет различные асимптоты при положительных и отрицательных значениях
переменной. При
x
график приближается сверху к асимптоте
4/1 xy
, а при
x
, также сверху к асимптоте
4/1 xy
.
Пример 18.
xxxy 2/
2
. Воспользуемся разложением бинома по переменной
z x 2 /
||/1
||
)/11(
||
)/21(
||
2/1
x
x
x
x
x
x
x
x
x
y
x
.
Функция имеет различные горизонтальные асимптоты
1y
, к которым график прибли-
жается снизу.
Пример 19.
)/1exp()2( xxy
. Разлагая показательную функцию по степеням перемен-
ной
xz /1
, получаем
xxxxxy
x
2/53)2/1/11)(2(
2
, то есть график функции
приближается к асимптоте
3 xy
, сверху при
x
, и снизу при
x
.
Пример 20.
)arctg(2/ xxy
. Используем разложение арктангенса при больших значени-
ях переменной
xxxxy
x
/12/2/)/12/(2/
,
xxxxy
x
/12/2/)/12/(2/
.
Функция имеет две различные наклонные асимптоты.
Пример 21.
))/11ln(1( xxxy
. Разлагаем логарифм по степеням
xz /1
, получаем
xxxxxxy
x
3/12/1))3/12/1/1(1(
32
, то есть функция имеет горизонтальную
асимптоту
y 1 2/
.
Примеры нелинейного поведения функций
Пример 22.
)exp(
22
xxy
. Формулу функции упростить нельзя. Поскольку экспонента
растет быстрее любой степенной функции, получаем
lim / exp( )
x
x x
2 2
0
, о есть при
больших значениях аргумента функция является экспоненциальной бесконечно малой.
Пример 23.
2
3
x
x
y
. Выделяя целую часть дроби при помощи деления, получаем
42
2
8
42
22
xx
x
xxy
x
, то есть при больших значениях переменной график
функции приближается к параболе
42
2
xxy
.
Пример 24.
x
x
y
1
)exp(1
. При больших положительных значениях переменной можно
пренебречь экспонентой в числителе
xy
x
/1
, то есть функция является бесконечно
малой первого порядка. Когда
x
числитель растет экспоненциально, поэтому
||/|)exp(| xxy
x
и функция является экспоненциально большой.
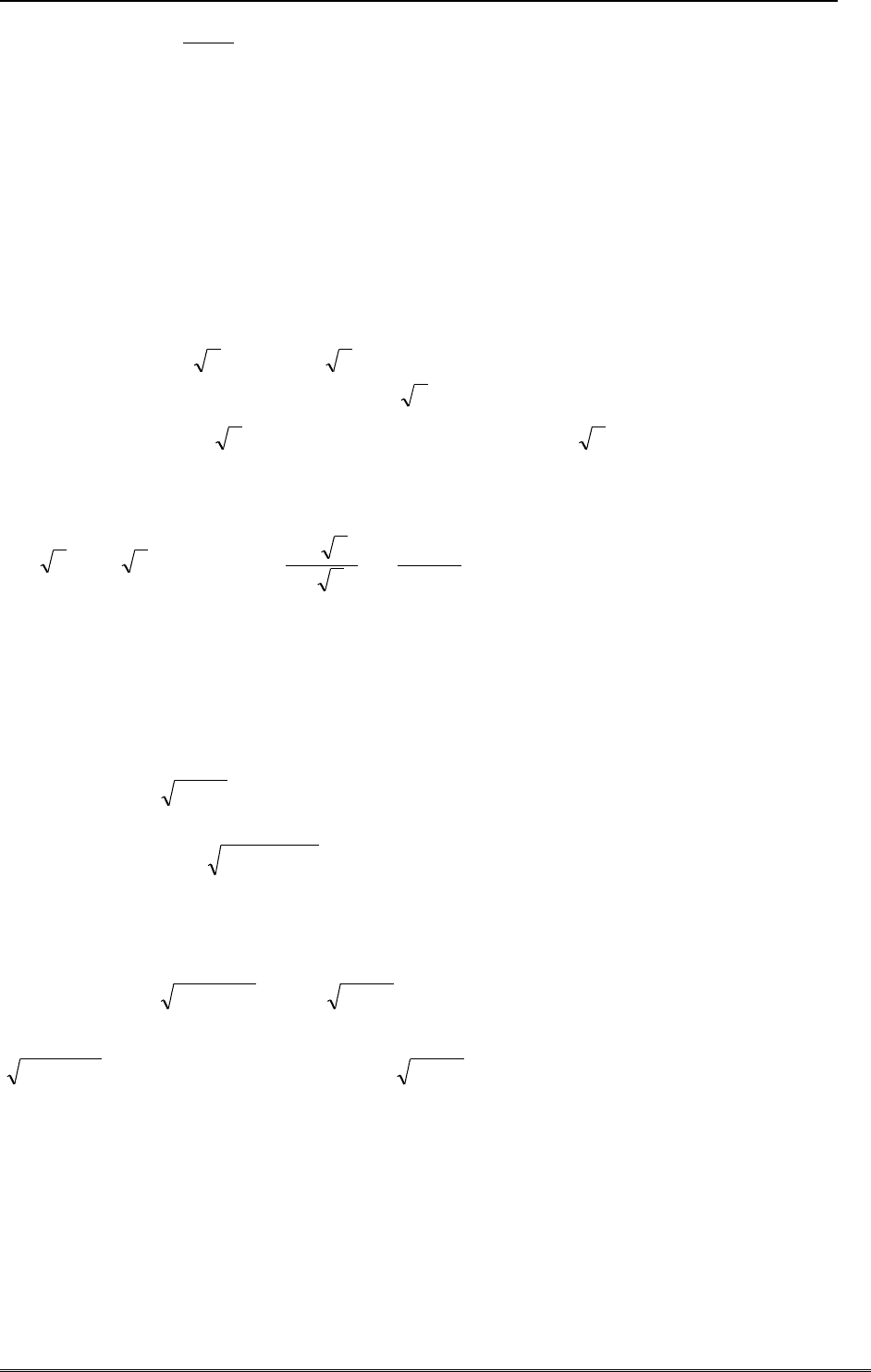
Основные элементарные функции (справочные сведения и примеры исследования)
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
21
Пример 25.
1
1
ln
2
x
x
y
. Преобразуем функцию, используя свойства логарифмов
y x x x x x x ln( ) ln( ) ln( ) ln( / ) ln( ) ln( / )1 1 1 1 2 1 1
2 2
, и отбросим бесконечно
малые
2
/1,/1 xuxz
, тогда
)ln(xy
x
, то есть при больших значениях переменной
функция является отрицательной бесконечно большой с логарифмическим ростом.
Сравнение функций в окрестности заданной точки
Сравнивать поведение функций в окрестности заданной точки можно различными спосо-
бами. Можно рассмотреть их частное или разность, определить по отдельности их поря-
док малости или порядок роста. Сравнение функций не является самоцелью, а является
частью какой то задачи, которая и определяет выбор способа сравнения функций.
Пример 26.
0),tg(),sin(
21
xxyxy
. Воспользуемся разложением Маклорена
для синуса и тангенса по переменной
z x
6/6/)sin(
2/33
xxzzz
,
3/3/)tg(
2/33
xxzzz
.
Отсюда видно, что функции являются эквивалентными бесконечно малыми порядка 1/2.
Их разность и частное
2/)tg()sin(
2/3
0
xxx
x
,
2/1
3/1
6/1
)tg(
)sin(
0
x
x
x
x
x
x
.
Пример 27.
0)),cos(1(2),sin()tg(
21
xxxyxxy
. Используем разложения Мак-
лорена синуса, косинуса и тангенса
2/)6/()3/()sin()tg(
333
0
xxxxxxx
x
,
32
0
))2/1(1(2))cos(1(2 xxxxx
x
, следовательно, сравниваемые функции являют-
ся неэквивалентными бесконечно малыми третьего порядка.
Пример 28.
2),1ln(,13
2
2
5
2
1
xxxyxy
. Разложим сравниваемые функции
в ряды Тейлора при помощи замены переменной
zx 2
и разложений Маклорена для
логарифма и бинома
5/)2(45/41)5/41(1)41(13)2(
0
5/12
5
2
xzzzzz
z
,
)2(33)31ln()1)2()2ln((
0
22
xzzzzz
z
, следовательно, сравниваемые функ-
ции являются неэквивалентными бесконечно малыми первого порядка.
Пример 29.
xxyxxy ,2,1
3
3
2
4
4
1
. Вынося старшую степень и используя
разложение Маклорена для бинома, получаем
||)/1/11(||1
4/153
4
4
xxxxxx
x
,
xxxx
x
3/13
3
3
)/21(2
.
Отсюда следует, что сравниваемые функции являются бесконечно большими первого по-
рядка, эквивалентными при
x
, а при
x
их частное стремится к -1.
Пример 31.
xxyxy ),ch(),sh(
21
. Используя понятие экспоненциального роста
и экспоненциальной малости, получаем следующие приближенные формулы
2/)exp(2/))exp()(exp()sh( xxxx
x
,
2/)exp(2/))exp()(exp()ch( xxxx
x
.
Отсюда видно, что сравниваемые функции имеют экспоненциальный рост и являются эк-
вивалентными.

Основные элементарные функции (справочные сведения и примеры исследования)
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
22
Пример 32.
xxxyxxy ),1ln(),12ln(
2
2
2
1
. Преобразуем сравниваемые
функции, используя свойства логарифмов и разложение Маклорена для логарифма
xxxxxxxxxx
x
/2|)ln(|2)/1/21ln(|)ln(|2)/1/21(ln()12ln(
2222
,
xxxxxxxxxx
x
/1|)ln(|2)/1/11ln(|)ln(|2)/1/11(ln()1ln(
2222
.
Отсюда видно, что сравниваемые функции являются эквивалентными бесконечно боль-
шими логарифмического роста.
Пример 33.
0),/1exp(|),|/1exp(
2
21
xxyxy
. Сравниваемые функции экспо-
ненциально малы. Для сравнения сделаем замену
||/1 xz
и рассмотрим частное
0)exp())/11(exp(
)exp(
)exp(
|)|/1exp(
)/1exp(
22
22
zzz
z
z
x
x
z
. Следовательно,
|)|/1exp()/1exp(
0
2
xox
x
.
Пример 34.
xxyey
xx
),1ln(),1ln(
21
. Преобразуем сложную показатель-
ную функцию к постоянному основанию
ln( ) ln( exp( ln( )))1 1
x x x
x
. Так как
)ln(xx
положительная бесконечно большая функция при
x
, разложим логарифмы по ма-
лым добавкам
u x exp( )
и
w x x exp( ln( ))
, и рассмотрим частное
0))ln(exp(
)exp(
))ln(exp(
)1ln(
)1ln(
))exp(1ln(
)))ln(exp(1ln(
xx
x
xx
u
w
u
w
x
xx
x
.
Следовательно, сравниваемые функции являются экспоненциальными бесконечно малы-
ми и
)1ln()1ln(
x
x
x
eox
.
Раскрытие неопределенностей
Раскрыть неопределенное выражение в формуле функции, - это значит исследовать пове-
дение функции в окрестности точки, где неопределенность имеет место. Для раскрытия
неопределенности необходимо исследовать вблизи этой точки поведение каждого из опе-
рандов, формирующих неопределенность. Следовательно, процедура раскрытия неопре-
деленностей базируется на методах локального сравнения функций. Часто под раскрыти-
ем неопределенности понимают лишь вычисление предельного значения функции в точке,
где неопределенность имеет место. Однако, задачу о раскрытие неопределенности можно
(и нужно!) поставить более широко, как задачу получения приближенной формулы для
функции в окрестности исследуемой точки (в такой постановке вычисление предела про-
исходит автоматически).
Неопределенности
0 ,/ ,0/0
Пример 35.
5,
)43(
16
2
x
x
x
y
. Числитель и знаменатель являются бесконечно ма-
лыми, то есть функция имеет неопределенность 0/0. Делаем замену переменной
x z 5
и используем разложение бинома
)5(
1818
))18/1(1(9
1)2/1(
))9/1(1((9
1)1(
)93(
11
2
0
22/1
2/1
2
xzz
z
z
z
z
z
y
z
.
Следовательно, вблизи
x 5
функция является бесконечно большой первого порядка.
