Алексеев Д.В. Конспекты по общему курсу математики

Подождите немного. Документ загружается.

Дифференцирование и интегрирование функций нескольких переменных

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева





VVV

dxdydzzyxgbdxdydzzyxfadxdydzzyxbgzyxaf ),,(),,()},,(),,({





),,(),,(),,(

VVV

dxdydzzyxfdxdydzzyxfdxdydzzyxf

В последней формуле объем фигуры представлен в виде суммы заполняющих ее непере-

секающихся фигур



VVVVV ,



Как и в случае двойного интеграла, свойство аддитивности позволяет свести вычисление

интеграла по произвольной области пространства к вычислению суммы интегралов по

выпуклым областям. Для этого необходимо только представить исходную область в виде

объединения выпуклых и непересекающихся областей.

Вычисление тройного интеграла в ортогональных криволинейных координатах

Наиболее просто тройной интеграл вычисляется по объему прямоугольного параллелепи-

педа

},,{ fzedycbxaV 

, грани которого параллельны координатным плос-

костям. Проекциями такого параллелепипеда на любую координатную плоскость являют-

ся прямоугольники, стороны которых параллельны координатным осям. В этом случае

тройной интеграл сводится к повторному по формуле





dzzyxgdydxdxdydzzyxg ),,(),,(

Если дополнительно подынтегральная функция является произведением трех функций,

зависящих только от одной из переменных

)()()(),,(

321

zfyfxfzyxg 

, тройной интеграл

превращается в произведение трех определенных интегралов













































dzzfdyyfdxxfdxdydzzfyfxf )()()()()()(

321321

Когда область интегрирования имеет более сложные границы, необходимо использовать

общие формулы сведения тройного интеграла к повторному интегралу.

Использование криволинейных координат в пространстве преследует туже цель, что и ис-

пользование криволинейных координат на плоскости, - свести процедуру интегрирования

по области с криволинейными границами к интегрированию по параллелепипеду. Основ-

ным моментом, возникающим при использовании криволинейных координат в простран-

стве, является запись элемента объема в криволинейных координатах. Ниже приводятся

соответствующие формулы только для двух типов ортогональных систем криволинейных

координат, - цилиндрических и сферических.

Цилиндрические координаты, называемые также полярными координатами в пространст-

ве, используются для вычисления тройных интегралов по областям, имеющим симметрию

кругового цилиндра. В наиболее распространенном случае взаимосвязи цилиндрических и

декартовых координат ось симметрии совмещается с осью аппликат, а угол отсчитывают

от положительного направления оси абсцисс против часовой стрелки, как и при переходе

к полярным координатам, то есть

)sin(),cos(



ryrx 

Для иллюстрации перехода к цилиндрическим координатам рассмотрим вычисление объ-

ема кругового цилиндра

};{:

222

dzcayxV 

. В цилиндрических координатах этот

цилиндр определяется неравенствами

};20,0{: dzcarV 



, которые задают

прямоугольный параллелепипед, ребра которого параллельны координатным осям.

Дифференцирование и интегрирование функций нескольких переменных

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Для составления интегральной суммы, выражающей объем, покроем рассматриваемый

цилиндр элементами цилиндрических слоев. Все эти элементы имеют, одинаковую высо-

ту

одинаковую толщину

и одинаковый угловой раствор



. Однако, чем дальше

расположен элемент от оси симметрии, тем длиннее его протяженность вдоль окружности



. Объем отдельного цилиндрического элемента приближенно оценивается как произ-

ведение высоты

на площадь элемента кольца



rdrddS 

, то есть интегральная сумма





dzdrdrdzdSV



Соответствующий этой сумме тройной интеграл легко вычисляется сведением к повтор-

ному интегралу

)(

cdadrdrdzdzrdrd

dzc













Сравнение формул для объема цилиндра, записанных через тройной интеграл в декарто-

вых и цилиндрических координатах, дает формулу перехода к цилиндрическим координа-

там в тройном интеграле от единичной функции









dzc

ayx

dzrdrddxdydz





222

Обобщение этой формулы на случай тройного интеграла по цилиндру от любой гладкой

функции трех переменных имеет вид









dzc

ayx

dzrdrdzrrfdxdydzzyxf





)),sin(),cos((),,(

222

Сферические координаты в пространстве используются для вычисления тройных интегра-

лов по пространственным областям, имеющим симметрию шара. Точка сферической сис-

теме координат задается радиус-вектором, который характеризуется длиной и двумя уг-

лами, задающими ориентацию радиус-вектора относительно двух опорных осей. Когда

центр сферической системы координат совпадает с началом декартовой системы коорди-

нат, а опорные оси совпадают с осями

, формулы связи между сферическими и

декартовыми координатами имеют вид

).cos(

),sin()sin(

),cos()s in(







Здесь

- длина радиус-вектора,



- угол между радиус-вектором и осью

, а



– угол

между проекцией радиус-вектора на координатную плоскость

и осью

. Элементар-

ной мерой объема в сферических координатах является объем шарового слоя толщины

с угловыми размахами





dr )sin(



ddrdrdV )sin(



(вывод будет приведен

ниже).

О замене переменной в тройном интеграле

Общая формула замены переменной в тройном интеграле основана на универсальной за-

писи элемента объема в виде модуля смешанного произведения

|),,(| dzkdyjdxidxdydz







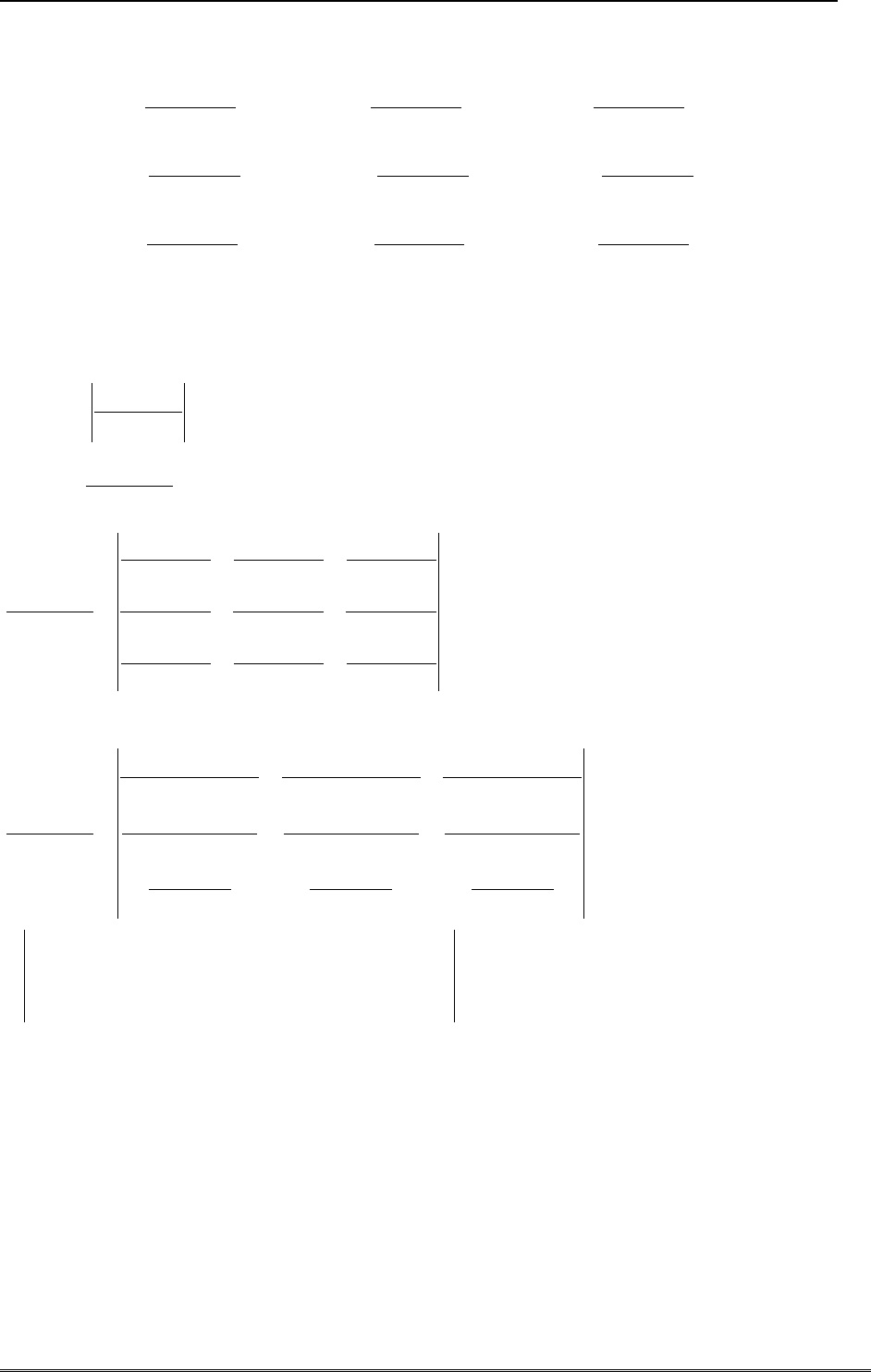
Дифференцирование и интегрирование функций нескольких переменных

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

При замене исходных декартовых координат на криволинейные ортогональные координа-

ты

),,(),,,(),,,( wvuzwvuywvux

получаем

wvux

wvuedv

wvux

wvuedu

wvux

wvuedxi













),,(

321





wvuy

wvuedv

wvuy

wvuedu

wvuy

wvuedyj













),,(

321





wvuz

wvuedv

wvuz

wvuedu

wvuz

wvuedzk













),,(

321





где

),,(),,,(),,,(

321

wvuewvuewvue



, - векторы ортонормированного базиса в точке

),,( wvu

Прямое вычисление модуля смешанного произведения дает следующую формулу для

элемента объема

dudvdw

wvuD

zyxD

dxdydz

),,(



Символ

),,(

wvuD

zyxD

обозначает якобиан преобразования

wvuz

wvuy

wvux

wvuD

zyxD





),,(),,(),,(

),,(

В случае перехода к сферическим координатам якобиан





























)cos()cos()cos(

)sin()sin()sin()sin()sin()sin(

)cos()sin()cos()sin()cos()sin(

),,(

zyxD

)sin(

0)si n()cos(

)cos()sin()sin()co s()sin()sin(

)sin()sin()cos()co s()cos()sin(













что и приводит к приведенной выше формуле для элемента объема.

Несобственные двойные и тройные интегралы

Несобственными двойными (тройными) интегралами называются интегралы от неограни-

ченных функций и интегралы по бесконечным областям на плоскости. Определение не-

собственных двойных интегралов, также как определение одномерных несобственных ин-

тегралов, основано на идее предельного перехода. Мы не будем описывать формальную

конструкцию этого предельного перехода, а лишь покажем, как эта идея реализуется в

конкретных ситуациях.

Двойные и тройные интегралы по бесконечной области интегрирования

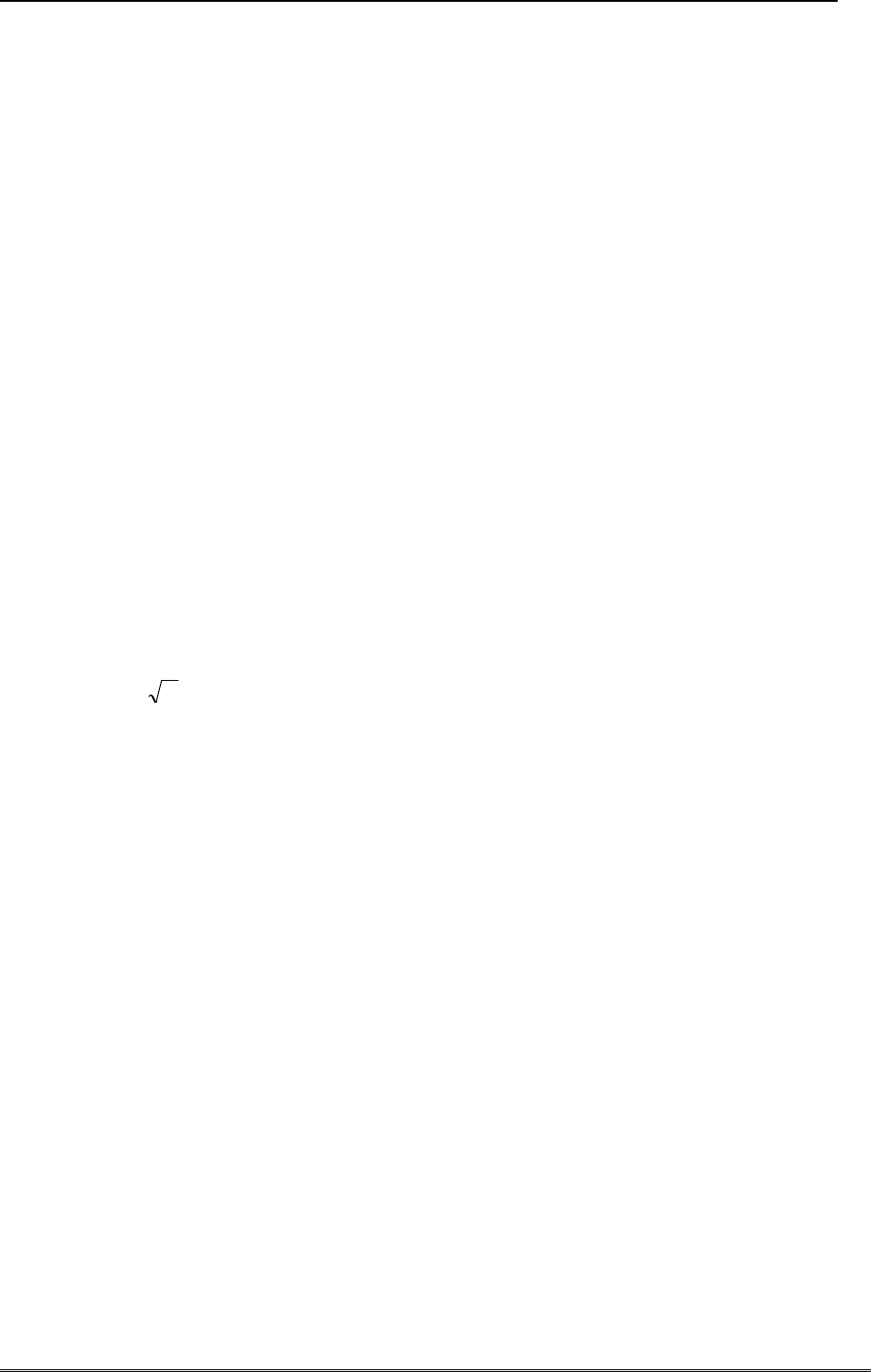
Дифференцирование и интегрирование функций нескольких переменных

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Идея определения двойного (тройного) интеграла от ограниченной функции по бесконеч-

ной области состоит в определении этого интеграла как предельного значения интеграла

по ограниченной области интегрирования. Эта процедура предельного перехода естест-

венным образом разбивается на следующие шаги.

 «Обрезаем» исходную область интегрирования

 Вычисляем получившийся интеграл обычным способом.

 Устремляем границы обрезания на бесконечность.

Пример. Вычислить интеграл







dxdyyx

)exp(

. Представим область интегрирова-

ния в виде прямоугольника, длины сторон которого устремляются к бесконечности. Так

как

)exp()exp()exp(

2222

yxyx 

, получаем

2222

)exp()exp()exp()exp()exp(























































dxxdyydxxdxdyyx

NyN

MxM

С другой стороны, представляя область интегрирования как круг бесконечного радиуса и

используя полярные координаты, имеем











































Rdrdrrdxdyyx ))exp(1(2)exp()exp(

Следовательно, мы не только вычислили исходный интеграл, но и показали, что











dxx )exp(

Двойные и тройные интегралы от неограниченных функций

Определение двойного (тройного) интеграла от неограниченных функции также основана

на идее предельного перехода, который осуществляется при помощи следующих шагов.

 Из области интегрирования «вырезают» малые области вокруг точек разрыва

функции.

 Вычисляют полученный интеграл обычным способом.

 Исследуют поведение этого интеграла при «стягивании вырезанных областей».

Интегралы от скалярных функций по геометрическим множествам

Длина дуги гладкой линии и криволинейный интеграл

Простейшим примером интеграла по геометрическому множеству является интеграл

вдоль кривой. Конструирование этого интеграла проще всего начать с интеграла, опреде-

ляющего длину гладкой линии, заданной векторной функцией

))(),(),(()( tztytxtr 



В этом случае элемент длины кривой, - это длина элементарного перемещения за «время»

, определяемое касательным вектором (скоростью линии)

))(),(),(()( tztytxtV









, -

dttVdL

|)(|





. Если при переходе из начальной точки дуги в конечную точку параметр

изменяется в интервале

ttt 

, длина линии дается интегральной суммой длин элемен-

тарных перемещений

Дифференцирование и интегрирование функций нескольких переменных

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева







dttVdL

|)(|11



которая переходит в пределе

N

в определенный интеграл, определяющий длину ду-

ги.





1|)(|

dLdttVL



Для нас важна структура этого интеграла, выражающаяся утверждением:

Длина дуги гладкой линии равна интегралу от единичной функции по элементарной мере

длины

dttVdL |)(|





Переход к произвольному криволинейному интегралу, - интегралу вдоль гладкой линии от

произвольной скалярной функции осуществляется при помощи замены в выписанной вы-

ше интегральной сумме единичной функции на произвольную функцию, заданную на рас-

сматриваемой линии









)(|)(|))((|)(|))(()(

dLLfdttVtrfdttVtrfdLLf



Площадь плоской фигуры и объем пространственного тела

Связь площади плоской фигуры с двойным интегралом подробно описана выше. Напом-

ним здесь только общую структуру интеграла для площади, описываемую утверждением:

площадь плоской фигуры равна интегралу от единичной функции по элементарной мере

площади. Произвольный двойной интеграл получается как обобщение этой формулы,

осуществляемое заменой единичной функции на произвольную функцию двух перемен-

ных, заданную в рассматриваемой области, то есть





dSS 1

, и



dSrf )(



Подобным же образом описывается и структура тройного интеграла, определяющего объ-

ем: объем тела равен интегралу от единичной функции по элементарной мере объема, а

произвольный тройной интеграл получается обобщением этой формулы, осуществляемым

заменой единичной функции на произвольную функцию трех переменных, заданную в

рассматриваемой области пространства





dVV 1



dVrf )(



Элементарную меру площади и объема можно задавать как в декартовых, так и в и криво-

линейных координатах. Часто встречающиеся формулы приведены в таблице.

Таблица 2 Формулы для элементарной меры

Координаты

Элементарная мера площади и объема

Декартовы

dxdydS 

dxdydzdV 

Полярные



rdrddS 

Цилиндрические

dzrdrddV





Сферические



ddrdrdV )sin(



Площадь гладкой поверхности и поверхностный интеграл

Интеграл, определяющий площадь гладкой поверхности может быть построен по анало-

гии с описанными выше конструкциями интегралов (поверхность называется гладкой, ес-

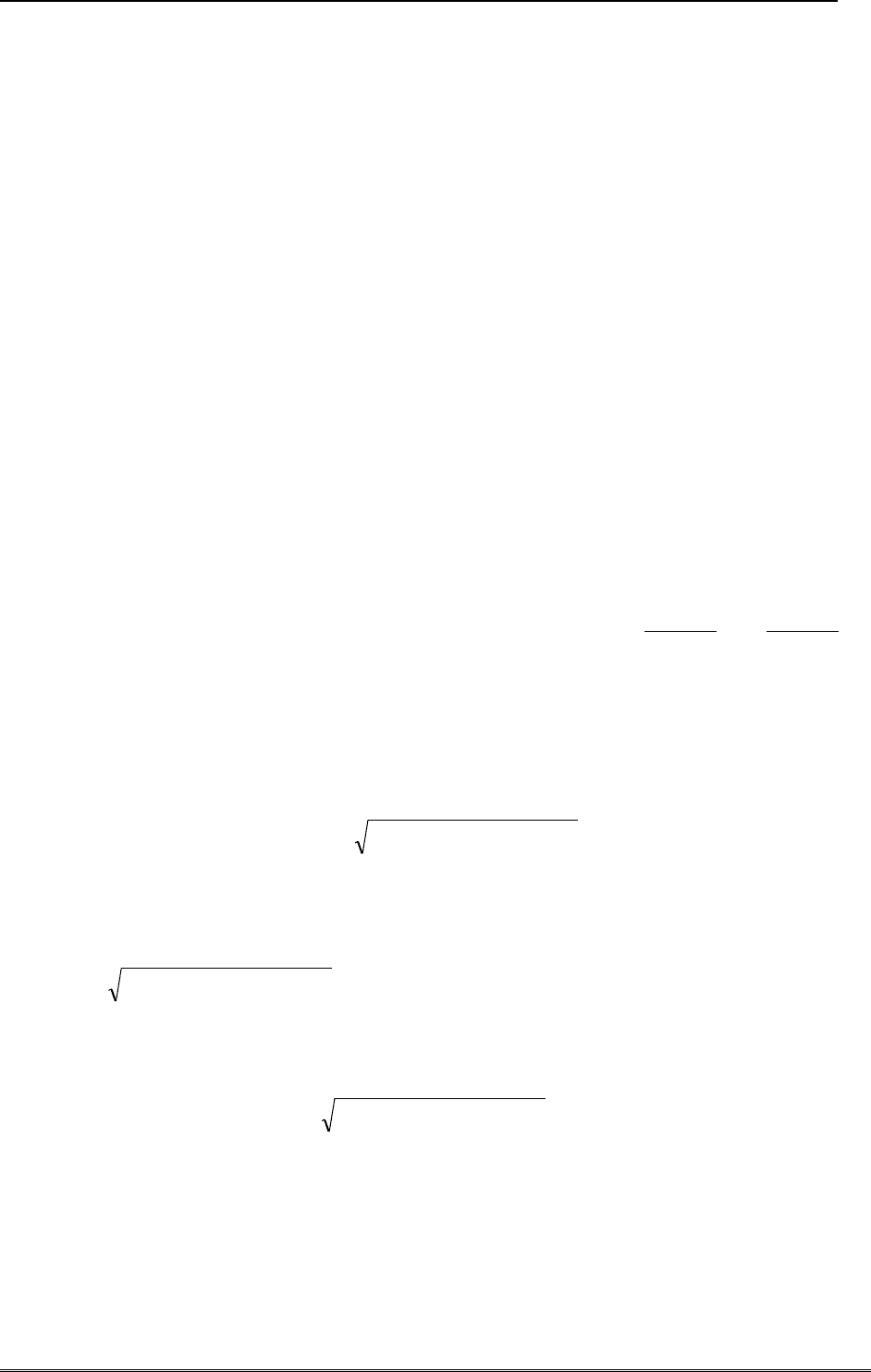
Дифференцирование и интегрирование функций нескольких переменных

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

ли в любой ее точке можно построить касательную плоскость). Для этого необходимо оп-

ределить элементарную (дифференциальную) меру площади гладкой поверхности. Для

определения этой меры воспользуемся аналогией с длиной гладкой кривой.

Для построения интегральной суммы покроем рассматриваемую криволинейную поверх-

ность элементами касательных поверхностей. Тогда площадь поверхности будет прибли-

женно равна сумме элементов касательных плоскостей







. Переход в этой инте-

гральной сумме к пределу

N

дает интеграл, определяющий площадь криволинейной

поверхности, называемый поверхностным интегралом.

Интеграл от произвольной скалярной функции по криволинейной поверхности определя-

ется, как и выше, путем замены в интегральной сумме единичной функции на произволь-

ную функцию, заданную на рассматриваемой поверхности













drfdrf

)()(



Приведенная конструкция поверхностного интеграла остается формальной до тех пор, по-

ка не будут построены конкретные формулы для элементарной меры поверхности, и на их

основе алгоритмы вычисления поверхностных интегралов.

Простейшим случаем поверхностного интеграла является интеграл, задающий площадь

поверхности графика функции двух переменных. В этом случае поверхность задается

уравнением, определяющим формулу функции

),( yxfz 

, а переменные функции пробе-

гают некоторую ограниченную область на координатной плоскости

),( yx

. Уравнение ка-

сательной плоскости в некоторой точке графика имеет вид

yxf









),(),(

то есть касательная плоскость перпендикулярна вектору

 

1),,(),,(),( 



 yxfyxfyxN



Из этого уравнения видно, что касательная плоскость образует с осью аппликат угол, оп-

ределяемый уравнением

||/)cos( NNk









, и на элементарный прямоугольник

dxdy

на

координатной плоскости

),( yx

проецируется элемент касательной плоскости, площадь

которого равна

dxdyyxfyxfdxdyyxNd

),(),(1|),(|













Последняя формула и задает элементарную меру площади поверхности графика функции

двух переменных. С ее помощью площадь поверхности графика выражается через двой-

ной интеграл по площади проекции поверхности на плоскость

),( yx











 D

dxdyyxfyxfd

),(),(11



Обобщение этой формулы на случай интеграла по поверхности графика от произвольной

скалярной функции имеет вид











 D

dxdyyxfyxfyxfyxFdzyxF

),(),(1)),(,,(),,(



Мы не будем описывать более общей конструкции элементарной меры площади поверх-

ности, поскольку в большинстве практически интересных случаев поверхность можно

разбить на части, каждая из которых может быть спроектирована на координатную плос-

кость, и рассматриваться как график некоторой функции. Кроме того, если поверхность

имеет высокую симметрию (круговой цилиндр или сфера), то для представления меры

площади таких поверхностей удобно использовать соответствующие криволинейные ко-

ординаты. Так элементарная мера площади цилиндра радиуса

задается формулой

Дифференцирование и интегрирование функций нескольких переменных

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

dzRdd





, а элементарная мера площади поверхности сферы радиуса

, - формулой



ddRd )sin(



Общая конструкция интеграла по геометрическому множеству

Как показывают приведенные выше конкретные примеры, центральным объектом в

структуре интеграла по геометрическому множеству является его элементарная мера. Ин-

теграл по этой мере от единичной функции дает полную меру рассматриваемого множест-

ва, - длину дуги кривой, площадь плоской фигуры или криволинейной поверхности, объем

пространственного тела. Следовательно, при построении общей теории интеграла внима-

ние должно быть сосредоточено именно на понятии меры геометрического множества.

Рассмотрим произвольное геометрическое множество

в многомерном пространстве.

Это множество может быть разбито на части, - подмножества

},,,{



AAA

, бесконеч-

ным числом различных способов. Для каждой пары точек любого из рассматриваемых

подмножеств определено понятие расстояния. С понятием расстояния связано понятие

внутренней точки множества. Точка

Aa 



называется внутренней, если существует рас-

стояние

, такое, что шар

dax  ||



находится внутри

. Множество, все точки которо-

го являются внутренними, называется открытым множеством.

Мерой называется числовая функция, определенная на подмножествах рассматриваемого

геометрического множества, которая обладает следующими свойствами:

 Мера не отрицательна

0)( A



 Для любого открытого множества

0)( A



 Для любой пары непересекающихся



множеств

)()()(

kjkj

AAAA





Отсюда следует, что если рассматриваемое множество может быть покрыто конечным или

бесконечным набором непересекающихся множеств



321

AAAA 



, его

мера

))()()()(

321321

  AAAAAA



является суммой мер покрывающих

множеств.

Говорят, что множество

имеет меру нуль

0)( S



, если оно может быть покрыто от-

крытыми множествами, суммарная мера которых меньше любого наперед заданного по-

ложительного числа.

При помощи понятия меры определяется понятие интегральной суммы и определенного

интеграла по произвольному геометрическому множеству от единичной функции.

Пусть геометрическое множество

покрыто конечными наборами открытых множеств,

такими, что















 AA





. Тогда суммы мер







)(1



Типичными примерами множеств меры нуль служат границы геометрических множеств. Так в одномерном

случае покрывающими подмножествами являются открытые отрезки, а границами отрезков являются точки.

Точка может быть помещена внутрь отрезка сколько угодно малой длины. Следовательно, точка на прямой

имеет меру нуль. На плоскости примерами множеств меры нуль являются системы изолированных точек и

линии, так как любую точку можно поместить внутрь сколько угодно малого открытого прямоугольника, а

линию можно покрыть набором открытых прямоугольников, суммарная площадь которых меньше любой

заданной положительной величины.

Дифференцирование и интегрирование функций нескольких переменных

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева









)(1



называются соответственно внутренней и внешней интегральными суммами

единичной функции на множестве

Рассмотрим пределы интегральных сумм, определяемые формулами









)(1lim)(



0)( 



0)( 













)(1lim)(



0)( 





0)( 









Если эти пределы существуют и равны, то получаемое в результате этого предельного пе-

рехода число называется мерой множества, или интегралом от единичной функции по

множеству

, -





AdA )(1)(



, а само множество называется измеримым.

Рассмотренное понятие интеграла от единичной функции по измеримому множеству

обобщается на случай интеграла от произвольной функции на измеримом множестве по

формуле











AAfAdAf

)()(lim)()(



0)( 



0)( 



где значение функции на подмножестве

определяется как ступенчатая функция, - на-

пример,

)(max)( afAf







, или

)(min)( afAf







Одним из важных следствий приведенной конструкции интеграла на множестве является

результат, который непосредственно следует из определения множества меры нуль:

интеграл по множеству меры нуль равен нулю. В заключении отметим, что все построен-

ные выше примеры интегралов от функций нескольких переменных, находятся в полном

соответствии с описанной общей конструкцией интеграла на геометрических множествах.

Дифференцирование и интегрирование векторных полей

Скалярные и векторные поля

Полями называют функции, заданные на точках пространства. Когда точки пространства

задаются с помощью координат трехмерного вектора

kzjyixr









, поля задаются

функциями нескольких переменных.

Простейшим примером поля является скалярное поле, задаваемое одной числовой функ-

цией

),,()( zyxrr







. Для задания векторного поля в трехмерном пространстве необ-

ходимо задать три координаты вектора

kzyxAjzyxAizyxArAr

zyx







),,(),,(),,()( 

то есть три числовых функции. Этот набор скалярных функций, называется координатны-

ми функциями векторного поля.

В некоторых задачах достаточно рассматривать зависимость полей только от двух коор-

динат, и векторные поля с двумя координатными функциями. Такие поля называются пло-

скими полями. Например, когда поле не зависит от аппликаты

jyixr







, скалярное поле

имеет вид

),()( yxrr







, а векторное поле

jyxAiyxArAr





),(),()( 

Всюду далее будут рассматриваться скалярные и векторные поля, которые определены во

всем пространстве, если иного не оговорено. Также будет предполагаться, что опреде-

Дифференцирование и интегрирование функций нескольких переменных

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

ляющие рассматриваемые поля функции всюду в области определения имеют производ-

ные любого необходимого порядка. Такие поля называются гладкими.

Потенциальное векторное поле и трехмерный набла-оператор

Векторное поле называется потенциальным, если оно может быть представлено как гра-

диент скалярной функции

rrA



















)()()(

)(grad)(





Скалярная функция

),,()( zyxr







, из которой при помощи дифференцирования полу-

чаются координатные функции векторного поля, называется скалярным потенциалом век-

торного поля, или кратко, - скалярным потенциалом.

Если рассматриваемое потенциальное векторное поле является двумерным, градиент со-

держит только две производных. Например, когда потенциал зависит только от абсциссы

и ординаты

),()( yxr







поле находится по формуле

rrA













),(),(

)(grad)(





Для удобства записи операции вычисления градиента от скалярного потенциала исполь-

зуют так называемый набла-оператор

















Этот оператор указывает все операции, которые необходимо выполнить для получения

градиента потенциала (вычисли частные производные и составь из них вектор). С помо-

щью набла-оператора градиент записывается кратко:

)(r







В следующей таблице приведены правила действия набла-оператора на скалярные поля,

являющиеся следствием обычных правил дифференцирования.

Операция

Формула

Дифференцирование линейной комбинации

)()())()(( rbrarbra







Дифференцирование произведения

)()()()())()(( rrrrrr







Дифференцирование частного

)(

)()()()(

))(/)((

rrrr

















Дифференцирование сложной функции

)())(( rr















При записи формул с набла-оператором необходимо проявлять аккуратность, - справа от

набла-оператора обязательно должна находиться функция, на которую он действует.

Дифференцирование векторных полей

Рассмотренная выше связь между потенциалом и векторным полем фактически является

определением операции дифференцирования скалярного поля. Отличительной особен-

В двумерном случае набла-оператор можно записать в виде











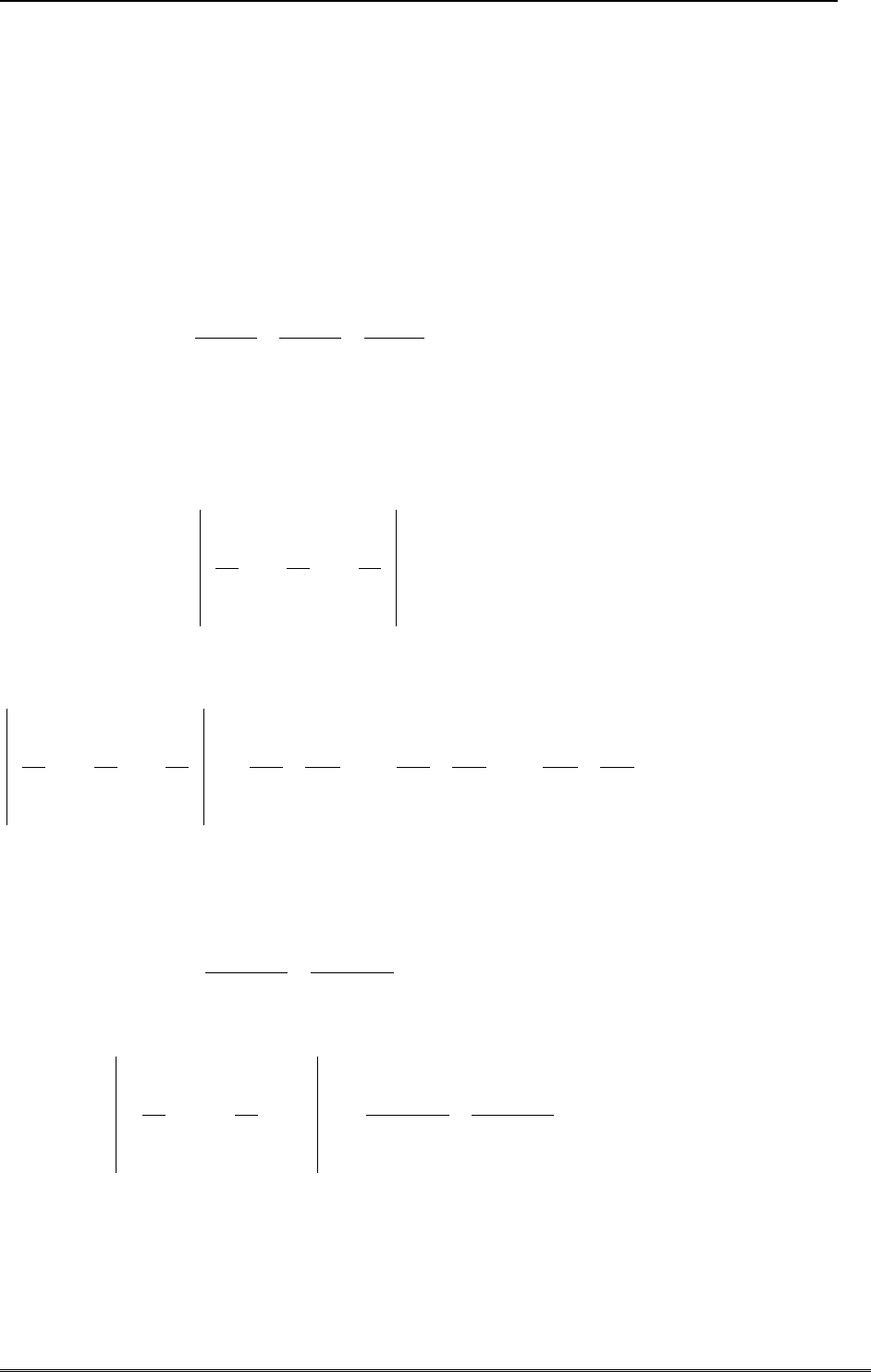
Дифференцирование и интегрирование функций нескольких переменных

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

ность этой операции является то, что с ее помощью осуществляется сопоставление век-

торного поля скалярному полю (потенциалу).

Отличительной особенностью дифференцирования векторных полей является то, что при

помощи действия набла-оператора на векторное поле

)(rA



можно получить как скалярное

поле

)(div rA



, называемое дивергенцией векторного поля, так и векторное поле

)(rot rA



называемое ротором векторного поля.

Дивергенция и ротор

Дивергенция векторного поля вычисляется по правилу, подобному правилу вычисления

скалярного произведения векторов

rArA













)(

)()(div



То есть дивергенцию можно символически представить как «скалярное произведение» на-

бла-оператора на векторное поле.

Ротор векторного поля вычисляется при помощи «векторного произведения» набла-

оператора на векторное поле по правилу

)()()(

)()(rot

rArArA

zyx

kji

rArA

zyx













Однако, при раскрытии определителя необходимо следить за тем, чтобы операторы диф-

ференцирования располагались строго слева от координатных функций































































rArArA

zyx

kji

zyx











)()()(

В последней формуле аргументы у координатных функций векторного поля для краткости

записи опущены.

Для плоского поля в рассмотренном выше примере формула для дивергенции имеет вид

yxA

rArA









),(

)()(div



а ротор имеет отличную от нуля только

координату

























yxA

yxAyxA

kji

),(

0),(),(

0)(







По поведению дивергенции и ротора векторные поля могут быть разбиты на два следую-

щих класса:

 Поле называется вихревым, если всюду в области определения

0)(div rA



 Поле называется потенциальным, если всюду в области определения

0)(rot rA

