Алексеев Д.В. Конспекты по общему курсу математики
Подождите немного. Документ загружается.

Сведения из элементарной математики 12
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Поведение функции
a
acbD 4
2
0y
при
);( x
0a
0D
0y
при
);( x
0a
0D
0y
при
);(
21
xxx
,
0y
при
);();(
21
xxx
0a
0D
0y
при
);();(
21
xxx
,
0y
при
);(
21
xxx
0a
0D
0y
при
1
xx
0a
0D
0y
при
1
xx
0a
0D
Приведенная классификация качественных разновидностей квадратичных функций опи-
рается на важный технический прием, называемый выделение полного квадрата
))((
22
xacbxaxy
.
Этот прием используется в самых разнообразных задачах, где встречается квадратичная
функция (вплоть до интегрирования!). Коэффициенты в представлении квадратичной
функции в виде полного квадрата вычисляются при помощи прямого сравнения коэффи-
циентов при одинаковых степенях переменной в обеих частях равенства
aaaxaxcbxax
222
2
.
2
4
,
2 a
D
a
b
.
В результате исходная квадратичная функция представляется в виде
2
2
42 a
D
a
b
xay
.
Когда дискриминант отрицателен, знак квадратичной функции определяется знаком ко-
эффициента при старшей степени переменной.
Когда дискриминант положителен, квадратичная функция может быть разложена по фор-
муле «разность квадратов» в произведение линейных сомножителей
)()(
2222
21
xxxxa
a
D
a
b
x
a
D
a
b
xay
.
Отсюда сразу следуют формулы для нулей квадратичной функции, - корней квадратного
уравнения
a
Db
xcbxax
2
,0
2,1
2
.
При обращении дискриминанта в нуль, корни квадратного уравнения совпадают, и его
разложение на элементарные сомножители принимает вид
a
b
xxxay
2
,)(
1
2
1
.

Сведения из элементарной математики 13
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
В этом случае говорят, что уравнение имеет один корень кратности два.
Деление квадратного уравнения общего вида на коэффициент при старшей степени дает
так называемое приведенное квадратное уравнение
acqabpqpxx /,/,0
2
.
Если корни приведенного квадратного уравнения существуют, то его разложение на эле-
ментарные сомножители принимает вид
2121
2
21
)()()( xxxxxxxxxxy
.
Из сравнения последнего разложения с приведенным уравнением следует теорема Виета,
которую удобно записать в виде системы
.
,
,04
21
21
2
pxx
qxx
qp
Теорему Виета удобно использовать для формулировки разнообразных утверждений от-
носительно корней квадратного уравнения. Например, утверждение «корни приведенного
квадратного уравнения положительны» записывается в виде следующей системы нера-
венств
.0
,0
,04
2
p
q
qp
.
Функции
Функции выражают количественную взаимосвязь между несколькими переменными ве-
личинами, которую называют функциональной зависимостью. В простейшем случае это
взаимосвязь между двумя переменными. Наличие функциональной зависимости означает,
что по исходному числу, - значению независимой переменной (аргумента) мы вычисляем
значение зависимой переменной (функции) при помощи некоторой формулы
)(xfy
.
Напомним некоторые основные определения, связанные с понятием функции.
Областью определения функции
)( fD
называется множество значений аргумента, при
которых формула функции непротиворечива.
Областью значений функции
)( fE
называются числовое множество, получаемое по фор-
муле функции, когда аргумент пробегает всю область определения.
Графиком функции
)( fG
называется множество пар
))(,( xfx
, получаемое, когда аргу-
мент пробегает всю область определения. Наглядно график можно представить как мно-
жество точек на плоскости.
Функция называется однозначной, если каждому значению переменной из области опре-
деления соответствует одно значение функции, в противном случае она называется много-
значной.
Однозначная функция называется взаимнооднозначной, если каждому значению функции
соответствует единственное значение ее аргумента.
Функция, получаемая «встройкой» одной формулы внутрь другой формулы называется
сложной функцией, или композицией функций (например,
3
sin)( xxf
).

Сведения из элементарной математики 14
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Две взаимнооднозначных
)(),( xgxf
функции называются обратными, по отношению друг
к другу, если справедливы тождества
xxfgxgf ))(())((
.
Производная и интеграл
Понятие производной определяет важный класс так называемых дифференцируемых
функций.
Функция
)(xf
называется дифференцируемой в точке
ax
, если ее значение вблизи
этой точки может быть представлено в виде
)())(()()( axoaxafafxf
Здесь
)(af
, - константа, называемая производной функции
)(xf
в точке
ax
. Символ
)( axo
обозначает функцию, которая убывает быстрее разности
ax
, когда переменная
x
приближается к
a
(это обозначают формулой
ax
).
Точки области определения функции, в которых производная существует, называют обла-
стью существования производной. То есть производную можно также рассматривать как
функцию, сопоставляющую точкам из области существования производной значения про-
изводной. Операция вычисления производной называется дифференцированием.
С понятием производной связаны два важнейших понятия, которые широко используются
при решении разнообразных задач.
Формула
))(()( axafafy
задает прямую линию, которая является касательной к
графику функции
)(xf
в точке с координатами
))(;( afa
на координатной плоскости
),( yx
.
Если функция
)(tf
описывает некоторый процесс во времени, то производная
)()( tftv
определяет мгновенную скорость этого процесса. То есть для значений
t
близких к
0
t
))(()()(
000
tttvtftf
,
0
0
0
)()(
)(
tt
tftf
tv
.
Понятие интеграла связано с действием, обратным к дифференцированию, которое назы-
вается интегрированием.
Постановка задачи интегрирования может звучать примерно так:
по функции
)(xf
найти функцию
)(xF
, чтобы всюду на области определения
)(xf
вы-
полнялось равенство
)()( xfxF
.
Функцию
)(xF
называют первообразной функции
)(xf
. Поскольку производная любой
константы равна нулю, ясно, что первообразная определяется с точностью до постоянного
слагаемого.
Первообразная может быть определена однозначно, если условиями задачи задано ее зна-
чение в некоторой точке. Для достаточно часто встречающегося случая непрерывных
функций первообразная может быть записана в виде
x
a
dxxfaFxF
11
)()()(
,
где символ
x
a
dxxf
11
)(
называется определенным интегралом функции
)(xf
по интервалу
),( xa
.

Сведения из элементарной математики 15
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Определенный интеграл имеет ясный геометрический смысл, который проще всего понять
для случая малых значений разности
ax
.
По определению дифференцируемой функции
))(()()( axafaFxF
,
то есть определенный интеграл это «площадь» прямоугольника с «шириной основания»
ax
и «высотой»
)(af
. Определения, входящие в эту формулировку, взяты в кавычки
потому, что связанные с ними значения могут быть как положительными, так и отрица-
тельными.
Для произвольного интервала интегрирования, определенный интеграл от непрерывной
функции, это просто сумма определенных интегралов по разбиению интервала интегриро-
вания
),( ba
на малые интервалы
Nabx /)(
)()()())()(()(
00
1
aFbFxxfxFxFdxxf
N
k
k
N
k
kk
b
a
,
где значения первообразной вычисляются в точках
xkax
k
,
Nk ,1,0
.
Приведенная приближенная формула становится точной, когда число интервалов разбие-
ния устремляется к бесконечности. Эта точная формула называется формулой Ньюто-
на-Лейбница
)()()( aFbFdxxf
b
a
.
Определенный интеграл также имеет ясную физическую интерпретацию, применяемую в
многочисленных задачах. Пусть
)()( txtV
, - мгновенная скорость изменения характери-
стики
)(tx
некоторого физического процесса. Тогда определенный интеграл дает прира-
щение рассматриваемой характеристики за произвольный конечный интервал времени
t
t
dttVtxtx
0
110
)()()(
.

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Начальные сведения по математической статистике
Задачей математической статистики является извлечение количественной информации из
данных наблюдений или измерений, искаженных случайными воздействиями. Например,
в измерительной системе присутствуют случайные помехи, или на данные наблюдений
влияют многочисленные неконтролируемые факторы. По этой причине, описание данных,
искаженных случайными воздействиями должно опираться на вероятностные модели,
которые строятся при помощи аппарата теории вероятностей, а одной из главных задач
математической статистики, является разработка количественных критериев, на основе
которых можно аргументировать соответствие (адекватность), построенной вероятност-
ной модели исходным данным.
Статистическое исследование принято разбивать на следующие этапы:
Планирование сбора данных (планирование проведения эксперимента),
Анализ данных, полученных из наблюдений или эксперимента,
Проверка гипотез, выдвинутых в ходе анализа данных.
Этапы статистического исследования можно также выразить и в виде триады:
Исходные данные,
Вероятностная модель данных,
Проверка адекватности модели исходным данным.
Для иллюстрации основных идей статистических рассуждений, рассмотрим следующую
простую задачу.
Британская инструкция эксплуатации подвижного состава требует, чтобы железнодо-
рожные вагоны следовали порожняком не более 50% времени. В ходе четырехсот случай-
ных проверок вагонов на конкретном участке железной дороги 220 вагонов оказались
пустыми. Можно ли на основе полученных данных утверждать, что на проверенном уча-
стке железной дороги инструкция эксплуатации нарушена?
Исходными данными задачи являются два числа:
число проверок – 400,
число пустых вагонов – 220.
Рассуждения, приводящие к вероятностной модели данных, могут выглядеть примерно
следующим образом. Тщательное планирование проверок (сбора данных) исключила не
только повторную проверку одного вагона, но и гарантировала независимость каждой
проверки от всех остальных. Обнаружение пустого вагона будем считать «успехом», а за-
груженного вагона, - неудачей. Поэтому в качестве вероятностной модели данных вполне
подойдет последовательность испытаний Бернулли, а в качестве условия соблюдения ин-
струкции эксплуатации принимаем следующий количественный критерий, - «вероятность
успеха
2/1p
».
Теперь необходимо получить количественный критерий, который позволит проверить ги-
потезу «инструкция соблюдается (
2/1p
)», против альтернативы «инструкция нарушена
(
2/1p
)». Так как число проверок
400n
велико, воспользуемся для описания распре-
деления данных наблюдений нормальным приближением
),( pqnpnN
для биноминаль-
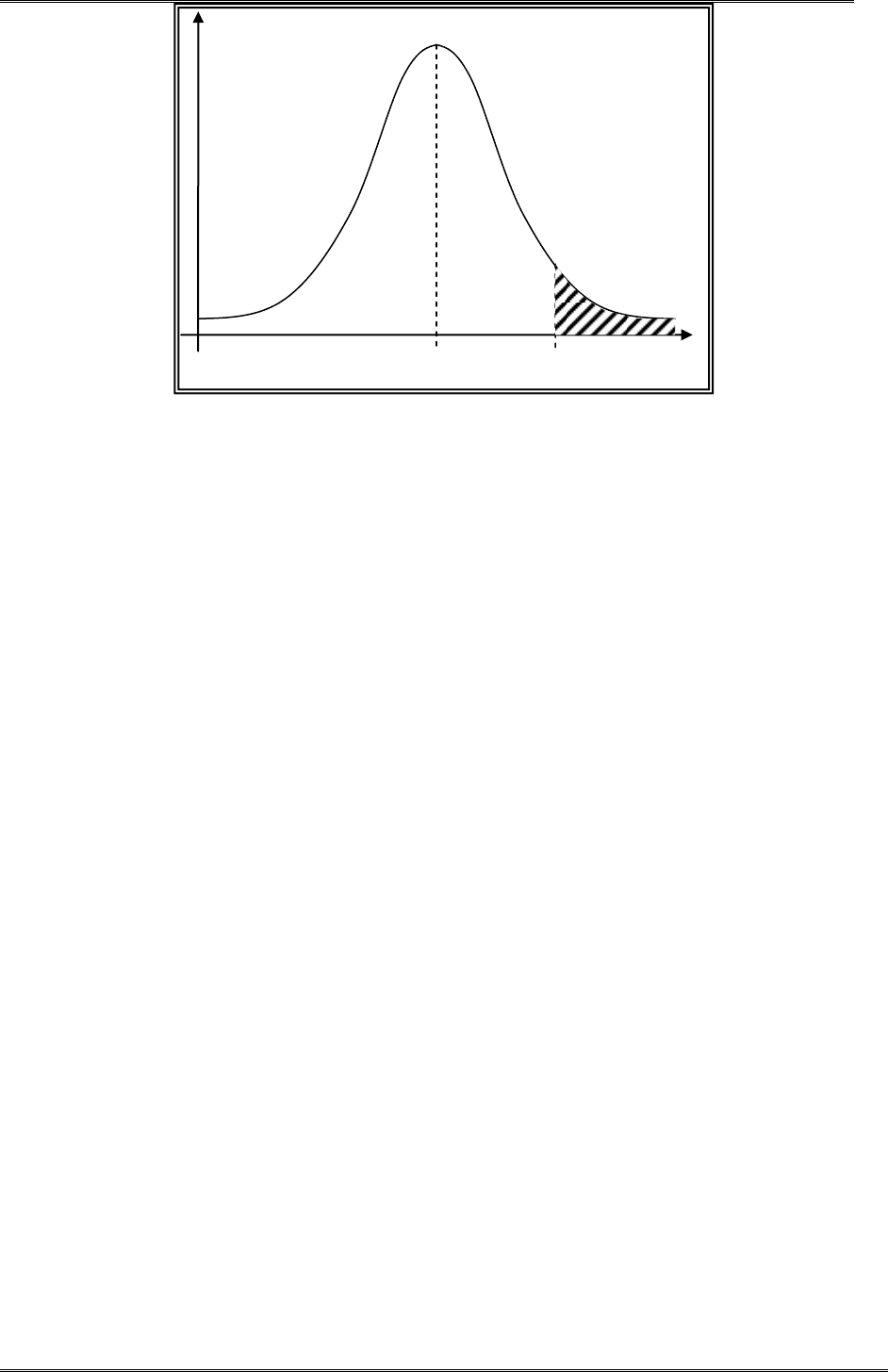
ного распределения, и отметим положение полученной точки наблюдения. Положение
точки наблюдения
220k
для распределения соответствующего
2/1p
приведено на
рисунке.
2
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Площадь заштрихованного «хвоста» распределения равна вероятности события «число
«успехов» больше наблюдаемого». Говоря иначе, площадь хвоста распределения указыва-
ет, с какой вероятностью при проведении аналогичных проверок будет получено значение
числа «успехов» больше наблюдаемого. Именно значение этой вероятности и выбирается
в качестве количественного критерия проверки гипотезы. Поскольку при увеличении
p
,
распределение смещается вправо, а при уменьшении
p
, - влево, малые значения площади
хвоста свидетельствуют против гипотезы «инструкция соблюдается».
Описанная вероятность (площадь хвоста), характеризующая риск принятия ложной гипо-
тезы, называется уровнем значимости основной (или нулевой) гипотезы относительно
рассматриваемой альтернативной гипотезы, и обозначается символом
SL
(significance
level). В нашем случае
%3,2023,0)210/)200()220( kPkPSL
, где для числен-
ной оценки использовались таблицы нормального распределения. Так как эта вероятность
мала, следует, по крайней мере, сильно усомниться в справедливости проверяемой гипо-
тезы. Количественно это утверждение принято формулировать словами: «основная гипо-
теза отвергается на уровне значимости 2,3%», то есть мы отвергаем гипотезу «инструкция
соблюдается» с вероятностью ошибки 2,3%.
Следует заметить, что количественные критерии уровня значимости, на котором отверга-
ется выдвинутая гипотеза, сильно зависят как от критериев строгости, принятых в той об-
ласти знаний, к которой относится рассматривая задача, так и от последствий, к которым
может привести принятие ошибочного решения, принятие ложной гипотезы (так называе-
мая ошибка первого рода) или отклонения правильной гипотезы (так называемая ошибка
второго рода). Стандартная трактовка численных значений уровня значимости будет при-
ведена ниже, при более подробном обсуждении проверки гипотез.
Выборки, распределенные по нормальному закону
Выборка случайной величины из нормального распределения является простейшей моде-
лью математической статистики. Хотя предположения, лежащие в основе этой модели,
довольно редко реализуются на практике, данная модель удобна для начального изучения
потому, что все получаемые на ее основе выводы можно продемонстрировать с помощью
достаточно простых вычислений. Именно уверенность, полученная при изучении про-
стейших моделей, позволяет при изучении более сложных моделей проследить за основ-
ными идеями, не вникая в технические детали, и быть уверенным, что в основе излагае-
мых результатов лежит научная аргументация, а не «шаманские» доводы.
200
0
220
3
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Измерение одной величины на фоне нормального шума
Рассматривается задача об измерении одной характеристики на фоне нормально распре-
деленных помех, то есть измеряемая случайная величина задается формулой
zax
ˆ
ˆ
, в
которой «шум»
z
ˆ
имеет распределение
),0(
N
.
Исходными данными рассматриваемой задачи является набор значений случайной вели-
чины, полученный в результате наблюдений или измерений, - выборка конечного объема
),,,,(
321 n
xxxx
(объемом выборки называется число ее элементов). При проведении дру-
гой серии измерений того же объема, в общем случае, получится другая выборка. Следо-
вательно, при рассмотрении выборок измерении мы имеем дело с набором случайных ве-
личин
)
ˆ
,,
ˆ
,
ˆ
,
ˆ
(
321 n
xxxx
. Целью задачи является получение максимальной информации о
значении измеряемой величины
a
, на основе полученной выборки результатов измере-
ний.
Опираясь на постулируемую в модели структуру измеряемой случайной величины, вы-
двигаются следующая гипотеза: измеряемая случайная величина
x
ˆ
распределена по закону
N a( , )
(вспомните о линейном преобразовании случайной величины). Задачей исследо-
вания является проверка на основе результатов измерений (выборки) всех предположений,
формирующих гипотезу, а именно:
Оценка значения параметров распределения
,a
;
Проверка того, что распределение является нормальным.
При этом дополнительно предполагается, что случайные величины набора являются неза-
висимыми, и эта независимость обеспечивается добросовестностью экспериментатора.
Приняв основную гипотезу, мы предположили, что значения измеряемой случайной вели-
чины сосредоточены около среднего значения
a
в интервале, измеряемом величиной
стандартного отклонения
, и первой задачей является построение функции выборки, ко-
торая оценивает среднее значение с разбросом существенно меньшим чем
.
Подобные задачи решаются при помощи функций выборки данных, которые оценивают
интересующие параметры и достаточно слабо меняются при изменении элементов выбор-
ки (такие функции называются статистиками).
Оценка параметра
a
Задача оценки параметра
a
решается так называемой статистикой выборочное среднее:
n
i
i
x
n
x
1
ˆ
1
ˆ
.
Используя преобразование характеристических функций при линейных преобразованиях
и суммировании статистически независимых слагаемых, нетрудно показать, что статисти-
ка выборочное среднее распределена по закону
)/,( naN
(см. главу о теории вероятно-
стей). Следовательно, значения статистики выборочное среднее сосредоточено около зна-
чения
a
измеряемой случайной величины в интервале, характеризуемом параметром
n/
. Так как в теоретическом пределе
n
, разброс значений статистики выборочное
среднее обращается в нуль, говорят, что статистика выборочное среднее дает состоятель-
ную точечную оценку измеряемой величины
a
.
Так как нормально распределенная случайная величина может принимать произвольные
значения, требует пояснения сделанное выше утверждение: «значения статистики выбо-

4
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
рочное среднее сосредоточены в интервале, измеряемом величиной
n/
». Покажем, что
это утверждение имеет вероятностный характер.
Поскольку статистика выборочное среднее имеет распределение
)/,( naN
, нормиро-
ванная случайная величина
)//()
ˆ
(
ˆ
naxu
имеет распределение
N( , )0 1
. Введем в
рассмотрение величины
)(pu
, называемые критическими точками нормального распреде-
ления и определяемые как решения неравенства
ppuupuP ))(
ˆ
)((
.
Если
n
i
i
x
n
x
1
1
измеренное (определенное по конкретной выборке) значение статистики
выборочное среднее, то вычисленное по нему значение нормированной случайной вели-
чины
)//()( nax
с вероятностью p попадает в интервал
))();(( pupu
. Следовательно,
значение измеряемой величины
a
с вероятностью
p
удовлетворяет неравенству
npuxanpux /)(/)(
.
Полученное неравенство называется интервальной оценкой для среднего значения. Интер-
вальная оценка указывает интервал, в который попадает значение оцениваемого парамет-
ра с заданной вероятностью. Интервал, в который с вероятностью
p
попадает значение
оцениваемого параметра называемого доверительным интервалом, а сама вероятность
p
- доверительной вероятностью. При этом в теоретическом пределе
n
границы дове-
рительного интервала стягиваются в точку независимо от вероятности, что находится в
полном соответствии с понятием состоятельной точечной оценки.
Поскольку на практике всегда приходится иметь дело с выборками наблюдений конечного
объема, при использовании интервальной оценки, возникает следующий нетривиальный
вопрос: какова должна быть доверительная вероятность
p
и как близко должны распола-
гаться границы доверительного интервала, чтобы интервальную оценку можно было счи-
тать удовлетворительной? Ответ на этот вопрос в каждом случае дает исследователь,
решающий задачу в зависимости от требований, предъявляемых к точности оценок в
конкретной области знаний, к которой относится решаемая задача. Например, исследо-
ватель может принять решение об увеличении объема выборки наблюдений для сужения
границ доверительного интервала.
Полученные оценки измеряемой случайной величины имеют следующие недостатки:
В них входит неизвестный параметр
(стандартное отклонение),
Они опираются на неподтвержденную гипотезу о нормальном распределении из-
меряемой случайной величины.
Дальнейшей целью является улучшение оценок, путем устранения этих недостатков.
Оценка стандартного отклонения
и оценка параметра
a
на основе t-распределения
Задача оценки стандартного отклонения решает статистика выборочная дисперсия
2
1
2
)
ˆˆ
(
1
1
ˆ
n
i
i
xx
n
S
.
Дальнейшее исследование статистических свойств выборочной дисперсии основывается
на следующей теореме об ортогональном разложении:

5
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Пусть статистически независимые случайные величины
nix
i
,3,2,1 ,
ˆ
имеют одинако-
вое распределение
N a( , )
. Тогда
2
2
2
1
2
ˆ
ˆ
)1(
ˆ
ax
n
Snax
n
i
i
,
где случайные величины
22
/
ˆ
)1(
Sn
и
2
)/)
ˆ
((
axn
статистически независимы и име-
ют распределения
-квадрат с
1n
и одной степенью свободы соответственно.
1
Из теоремы об ортогональном разложении следует, что случайная величина
22
/
ˆ
)1(
Sn
имеет распределение
- квадрат с
1n
степенью свободы. Поскольку плотность вероят-
ности распределения
- квадрат, в отличие от плотности нормального распределения, не
является симметричной функцией, для получения интервальной оценки стандартного от-
клонения границы интервала
))(),((
11
pRpL
nn
определяются как решения неравенств:
2/)1())(
ˆ
( ;2/)1())(
ˆ
(
1
2
1
2
ppRPppLP
nn
.
Если
2
1
2
)(
1
1
n
i
i
xx
n
S
- определенное по исходной выборке значение выборочной
дисперсии, то величина
22
/)1(
Sn
с вероятностью
p
попадает в интервал
)(/)1()(
1
22
1
pRSnpL
nn
,
)1/()()1/()(
1
22
1
2
npRSnpL
nn
.
Для исследования поведения полученной оценки в теоретическом пределе
n
, вос-
пользуемся приближенными формулами, выражающими границы интервала через соот-
ветствующие границы распределения
N( , )0 1
:
npunpRnpunpL
nn
2)()( ;2)()(
.
Тогда:
02/)1)((||
2/322
n
npuS
,
то есть статистика «выборочная дисперсия» является состоятельной точечной оценкой
дисперсии распределения.
С другой стороны, неравенство для величины
22
/)1(
Sn
сразу позволяет получить и ин-
тервальную оценку для неизвестного стандартного отклонения
:
)(/)1()(/)1(
1
2
1
2
pLSnpRSn
nn
,
или при больших значениях
n
:
22
)1(2/)(1)1(2/)(1 SnpuSnpu
.
Терема об ортогональном разложении позволяет также получить интервальную оценку
для параметра
a
, свободную от предположения об известном значении стандартного от-
клонения
. Эта оценка основывается на так называемом
t
- распределении Стьюдента,
которое определяется следующим образом: если независимые случайные величины
m
hh
ˆ
,
ˆ
1
1
Доказательство этой теоремы приводится в приложении
6
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
имеют распределение
- квадрат с одной и
m
степенями свободы соответственно, то
случайная величина
mm
hhmt
ˆ
/
ˆ
ˆ
1
имеет
t
- распределение с
m
степенями свободы.
Получим формулу для плотности вероятности
t
- распределения. Записываем функцию
распределения
)
ˆˆ
()2/1()
ˆ
/
ˆ
()2/1()
ˆ
/
ˆ
()
ˆ
(
2
1
2
11
thhmPthhmPthhmPttP
mmmm
,
(множитель 1/2 появился потому, что после возведения в квадрат неравенство допускает и
отрицательные значения переменной
t
).
Далее функция распределения вычисляется интегрированием произведения плотностей
- квадрат распределений с одной и
m
степенями свободы по треугольной области:
2/
0
2/1
2/
12/
0
2
21
2
2
)2/exp(
)2/(2
)2/exp(
2
1
)
ˆˆ
()2/1(
ut
M
m
dw
ww
m
uu
duthhmP
,
а плотность вероятности получается далее дифференцированием по переменной
t
:
.}2/)/1(exp{
)2/(2
1
2
)2/exp(
)2/(2
)2/exp(
2
1
)(
0
212/)1(
12/
/
0
2/1
2/
12/
0
2
dumtuu
mm
dw
ww
m
uu
du
dt
d
t
m
m
mut
m
m
m
Последний интеграл вычисляется при помощи замены переменной
ymtu 2)/1(
2
и оп-
ределения гамма – функции:
2/)1(2
)2/1(
)2/(
)2/)1((
)(
m
m
t
mm
m
t
.
Полученная плотность вероятности является четной функцией со степенным убыванием
при больших значениях переменной.
Применение
t
- распределения для получения интервальной оценки среднего значения ос-
новывается на том, что согласно теореме об ортогональном разложении, случайные вели-
чины
22
/)
ˆ
(
axn
,
22
/
ˆ
)1(
Sn
имеют распределение
- квадрат с одной и
1n
степе-
нями свободы соответственно, то есть, случайная величина
2
1
ˆ
/)
ˆ
(
ˆ
Snaxt
n
имеет
t
-
распределение с
1n
степенью свободы.
Определив граничные точки
t
- распределения как решения неравенства
ppttptP
nnn
))(
ˆ
)((
111
,
получаем, что вычисленное по исходной выборке значение величины
2
/)( Snax
с ве-
роятностью
p
попадает в интервал
))(),((
11
ptpt
nn
, то есть интервальная оценка для па-
раметра
a
имеет вид:
nSptxanSptx
nn
/)(/)(
2
1
2
1
.
Полученная интервальная оценка свободна от дополнительных предположений о величи-
не стандартного отклонения
, однако она все еще опирается непроверенную гипотезу
«результаты измерений имеют нормальное распределение».
