Алексеев Д.В. Конспекты по общему курсу математики
Подождите немного. Документ загружается.

17
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
В критерии Смирнова проверяется нулевая гипотеза: «обе выборки получены из совокуп-
ности описываемой одной и той же функцией распределения» против альтернативы: «вы-
борки получены из двух различных совокупностей, описываемых разными функциями рас-
пределения», при этом конкретный вид закона распределения не уточняется. Другими сло-
вами, по критерию Смирнова проверяется можно ли считать различие сравниваемых вы-
борок статистически значимым.
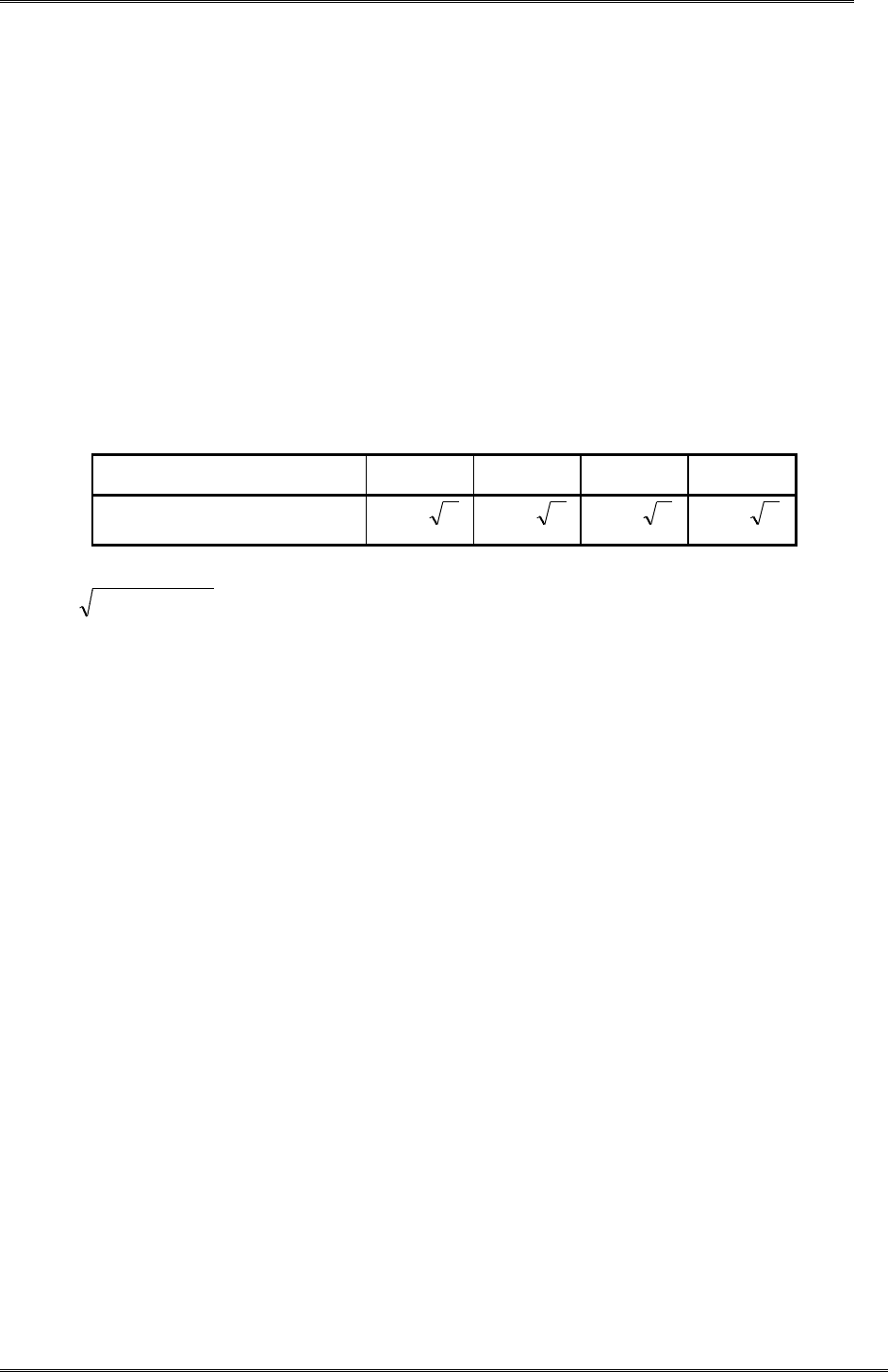
В качестве статистики критерия Смирнова используется максимальное «расстояние» меж-
ду эмпирическими функциями распределения сравниваемых выборок.
|)()(|max
2121
xGxFD
nn
x
nn
.
Уровень значимости для критерия Смирнова равен вероятности наблюдения в других ана-
логичных экспериментах значений статистики критерия, превосходящих полученную.
Значения этих вероятностей приводятся в указанных выше статистических таблицах. В
случае, когда объемы сравниваемых выборок больше сорока, наблюдаемые значения ста-
тистики критерия Смирнова можно сравнить с критическими значениями, вычисляемыми
по следующей таблице
Уровень значимости
SL
0,20
0,10
0,05
0,01
Критическое значение
c
D
n
~
/07,1
n
~
/22,1
n
~
/36,1
n
~
/63,1
где
)/(
~
2121
nnnnn
. Нулевая гипотеза принимается, если полученное по исходным вы-
боркам значение статистики критерия Смирнова не превосходит критическое значение.
Критерии, основанные на порядковых статистиках
Рассмотренные выше методы анализа данных использовали критерии, основанные на ста-
тистиках, - функциях от элементов выборки. Рассматриваемые ниже методы оперируют
только с порядковыми номерами элементов выборок в вариационных рядах, называемыми
рангами. Наименьшему элементу выборки приписывают ранг равный единице, следую-
щему за ним - ранг два, и так далее. Последнему члену ряда приписывается ранг равный
объему выборки. Если в выборке встречаются равные элементы, то каждому из них при-
писывают ранг равный среднему значению их номеров в вариационном ряду.
Следовательно, если
x
j
некоторый элемент исходной выборки, а
R x
j
( )
- его ранг то мы
приходим к представлению исходной выборки при помощи выборки рангов:
))(),(),(),((),,,(
321321 nn
xRxRxRxRxxxx
.
Процедура вычисления рангов элементов выборки называется ранжированием. Приводи-
мые ниже статистические критерии будут формулироваться при помощи некоторых
функций от рангов. Поскольку ранги являются порядковыми номерами элементов выбор-
ки, функции от рангов называются порядковыми статистиками, а рассматриваемые ста-
тистические критерии, - критериями, основанными на порядковых статистиках.
Критерий знаковых рангов Уилкоксона
Это критерий используется для проверки гипотезы о равенстве среднего значения элемен-
тов выборки некоторому заданному значению. Более точно: проверяется нулевая гипотеза
ax
против альтернативы
ax
. Для проверки гипотезы по исходной выборке
),,,(
321 n
xxxx
строится выборка разностей
ax
k
,
),,,,(
321
axaxaxax
n
, а затем -
выборка модулей разностей
|| axz
kk
),,(
21 n
zzz
, которая и ранжируется.

18
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Далее вычисляются суммы рангов отрицательных и положительных разностей
V R z
k
x a
( )
,
V R z
k
x a
( )
.
В пользу нулевой гипотезы будет свидетельствовать примерное равенство между найден-
ными суммами рангов:
V V
, тогда как значительная разница между этими суммами
будет свидетельствовать в пользу альтернативной гипотезы.
Более строго, при справедливости нулевой гипотезы различные ранги с равной вероятно-
стью могут принадлежать как к положительным, так и к отрицательным разностям. По-
скольку полная сумма рангов определяется только объемом рассматриваемой выборки
2/)1(
1
nnkVV
n
k
,
в качестве статистики критерия можно выбрать любую из величин
V
или
V
. Для даль-
нейшего определения уровня значимости удобно в качестве статистики критерия выбрать
меньшую сумму рангов
V V V
min( , )
.
Уровень значимости вычислим как вероятность появления на других выборках значения
статистики критерия меньше наблюдаемого
N
VM
VVVPSL
2
)(
)),min(
ˆ
(
,
где
M V( )
- число способов получить значения статистики критерия меньше наблюдаемо-
го. На основе полученного значения уровня значимости принимается решение относи-
тельно справедливости основной гипотезы
Критерий Уилкоксона-Манна-Уитни
Этот критерий используется для проверки нулевой гипотезы «две выборки получены из
одного и того же распределения» против альтернативы «выборки получены из различных
распределений».
Для проверки гипотезы обе рассматриваемые выборки
),,,(
1
321 n
xxxx
и
),,,(
2
321 n
yyyy
объединяются в единую выборку, которая и ранжируется. Далее находится сумма рангов
элементов принадлежащих каждой из сравниваемых выборок
S R x
x k
( )
,
S R y
y k
( )
.
При справедливости нулевой гипотезы, элементы обоих выборок будут достаточно рав-
номерно перемешаны в объединенном вариационном ряду, и следует ожидать примерного
равенства найденных сумм рангов
S S
x y
, а если справедлива альтернативная гипотеза,
следует ожидать значительного различия между этими суммами рангов.
Поскольку полная сумма рангов определяется только объемом сравниваемых выборок
S S N N N N
x y
( )( ) /
1 2 1 2
1 2
,
в качестве статистики критерия Уилкоксона - Манна-Уитни можно выбрать любую из
сумм
S
x
или
S
y
. Для удобства вычислений в качестве статистики критерия лучше исполь-
зовать сумму рангов выборки меньшего объема. Для определенности ниже будем считать,
что эта сумма
S
x
.

19
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
При справедливости нулевой гипотезы сумма рангов
S
x
является случайной величиной с
симметричным распределением относительно среднего значения
2/)1(
211
nnna
. По-
этому, уровень значимости нулевой гипотезы относительно рассматриваемой двусторон-
ней альтернативы вычисляется по формуле
)2
ˆ
()
ˆ
()|
ˆ
(|
xxxxxx
SaSPSSPaSaSPSL
.
Когда объем меньшей выборки больше 10, для вычисления уровня значимости можно
воспользоваться тем, что статистика
S
x
имеет приближенно нормальное распределение
N a( , )
с параметрами
2/)1(
211
nnna
и
12/)1(
2121
2
nnnn
, то есть статистика
12/)1(/)2/)1(
ˆ
(
ˆ
2121211
nnnnnnnSu
x
имеет распределение
)1,0(N
.
Ранговая корреляция Спирмена
Коэффициент ранговой корреляции Спирмена используется для проверки гипотезы о на-
личии статистически значимой зависимости между переменными в выборке парных на-
блюдений
)),();,();,();,((
332211 nn
yxyxyxyx
.
После стандартного ранжирования выборок
),,,(
321 n
xxxx
,
),,,(
321 n
yyyy
коэффициент
ранговой корреляции Спирмена вычисляется по формуле
n
k
kks
yRxR
nn
r
1
2
2
))()((
)1(
6
1
.
Для уяснения смысла коэффициента ранговой корреляции рассмотрим случай, когда меж-
ду переменными имеет место линейная зависимость
y Ax B
с положительным коэф-
фициентом пропорциональности. Тогда большим значениям
x
соответствуют большие
значения
y
, то есть и имеет место равенство рангов
R x R y
k k
( ) ( )
, и коэффициент ранго-
вой корреляции равен единице. Когда коэффициент пропорциональности отрицательный,
большим значениям
x
соответствуют меньшие значения
y
. В этом случае сумма квадра-
тов разностей рангов
3/)1())()((
2
1
2
nnyRxR
n
k
kk
,
и коэффициент ранговой корреляции равен -1.
Следовательно, в промежуточных случаях, когда явная зависимость между переменными
не прослеживается, значения коэффициента ранговой корреляции
1 1r
s
.
Оценка статистической значимости полученного коэффициента ранговой корреляции ос-
новывается на проверке нулевой гипотезы «переменные
x
и
y
независимы» против аль-
тернативы «переменные
x
и
y
зависимы».
В случае справедливости нулевой гипотезы коэффициент ранговой корреляции имеет
симметричное распределение на интервале (-1;1) с нулевым средним значением. Для вы-
борок достаточно большого объема (
10n
), вычисление уровня значимости можно сде-
лать, основываясь на том, что случайная величина
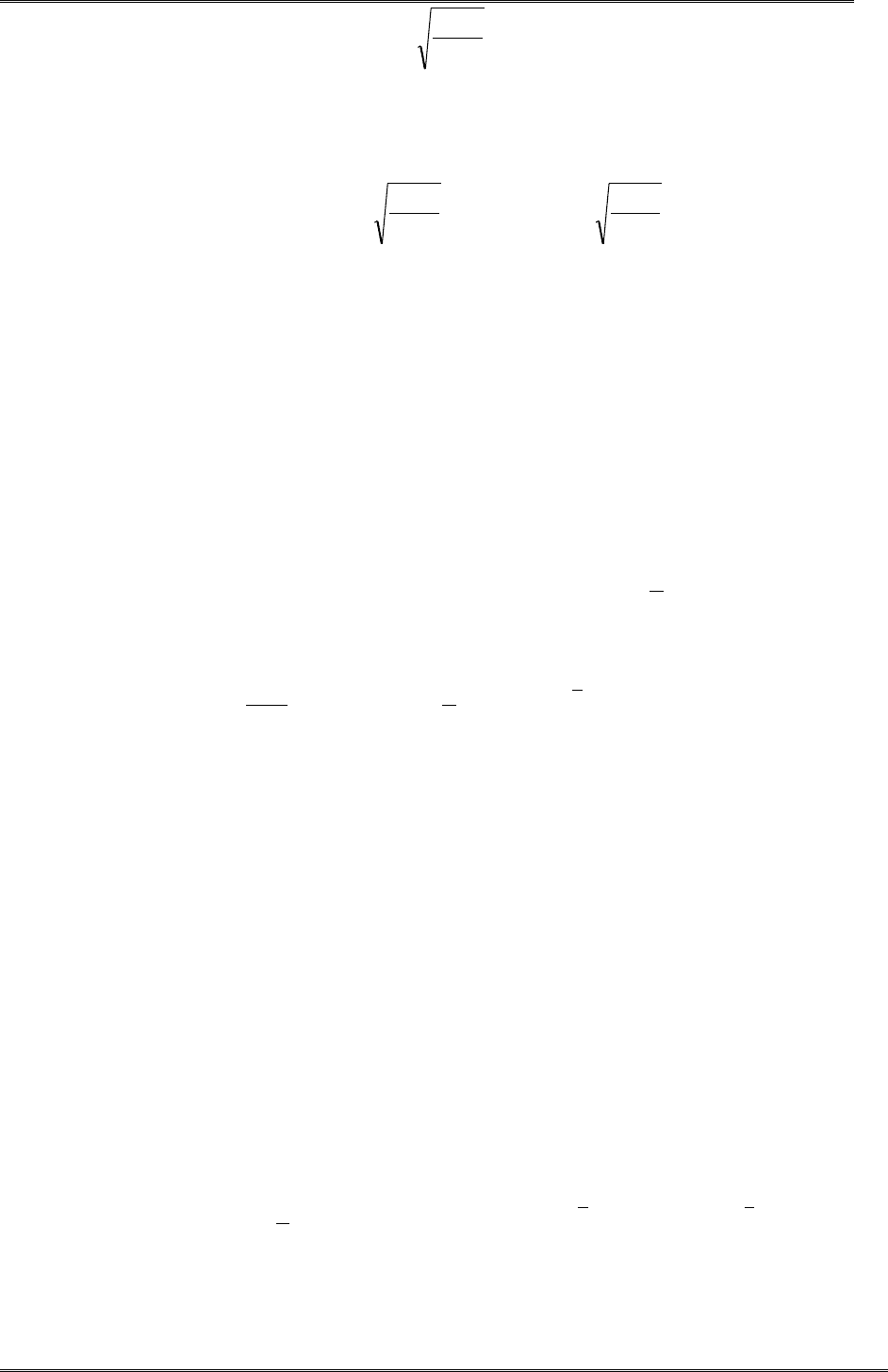
20
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
2
ˆ
1
2
ˆ
s
s
r
n
r
приближенно имеет
t
распределение с
2n
степенями свободы. Тогда уровень значи-
мости нулевой гипотезы против рассматриваемой альтернативы вычисляется по типичной
для двусторонних критериев формуле
2
2
2
2
1
2
||
ˆ
2
1
2
|||
ˆ
|
s
sn
s
sn
r
n
rtP
r
n
rtPSL
.
Поскольку малые значения уровня значимости свидетельствуют против нулевой гипоте-
зы, именно малые значения уровня значимости будут указывать свидетельствовать в
пользу зависимости между переменными
x
и
y
.
Приложения
Доказательство теорем об ортогональном разложении
Идея доказательства теорем ортогональности основана на рассмотрении совместной
плотности распределения вероятностей независимых случайных величин
k
x
ˆ
,
nk 2,1
,
имеющих одинаковое распределение
)1,0(N
. Их совместная плотность вероятности
n
k
k
n
n
k
kn
xxxx
1
22/
1
22/1
1
2
1
exp)2(2/exp)2(),(
.
Запишем выборочную дисперсию в виде
n
k
k
u
n
S
1
22
1
1
ˆ
,
xxx
n
xu
k
n
k
kkk
ˆˆˆ
1
ˆˆ
1
,
0
ˆ
1
n
k
k
u
,
где случайные величины
k
u
ˆ
уже не являются независимыми. Связь между
k
u
ˆ
и
k
x
ˆ
можно
записать с помощью матриц
nn
x
x
x
nnn
nnn
nnn
u
u
u
ˆ
ˆ
ˆ
/11/1/1
/1/11/1
/1/1/11
ˆ
ˆ
ˆ
2
1
2
1
,
где симметричная матрица преобразования обладает важнейшим свойством: ее квадрат
равен ей самой (проверьте!). Тогда прямым перемножением матриц получаем
n
n
n
n
x
x
x
nnn
nnn
nnn
xxx
u
u
u
uuu
ˆ
ˆ
ˆ
/11/1/1
/1/11/1
/1/1/11
ˆˆˆ
ˆ
ˆ
ˆ
ˆˆˆ
2
1
21
2
1
21
,
2
11
2
1
2
ˆ
1
ˆˆ
n
k
k
n
k
k
n
k
k
x
n
nxu
, или
2
2
2
1
2
1
2
ˆ
ˆ
)1(
ˆˆˆ
xnSnxnux
n
k
k
n
k
k
.
Отсюда следует, что совместная плотность вероятности

21
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
)2/exp(
2
1
exp
2
1
exp
2
1
2
1
2
xnux
n
k
k
n
k
k
то есть случайные величины
n
k
k
u
1
2
ˆ
и
2
ˆ
xn
статистически независимы. При этом случай-
ная величина
2
ˆ
xn
имеет распределение
- квадрат с одной степенью, а
n
k
k
x
1
2
ˆ
, - распре-
деление
-квадрат с
n
степенями свободы. Следовательно,
n
k
k
uSn
1
22
ˆ
ˆ
)1(
имеет рас-
пределение
-квадрат с
1n
степенью свободы.
Доказательство второй теоремы об ортогональном разложении аналогично, но использует
более громоздкую матрицу преобразований
A
, которая также обладает свойством
AA
2
.
Распределение Фишера
Пусть случайные величины
n
h
ˆ
и
m
h
ˆ
имеют распределения
-квадрат с
n
и
m
степенями
свободы соответственно. Тогда говорят, что случайная величина
)/
ˆ
/()/
ˆ
(
ˆ
,
mhnhF
mnmn
имеет распределение Фишера с
n
,
m
степенями свободы.
Плотность распределения Фишера получается способом, аналогичным использованному
при выводе плотности
t
-распределения: функция распределения для
mn
F
,
ˆ
записывается
через двойной интеграл от произведения плотностей двух
-квадрат распределений по
треугольной области:
)/(
0
12/12/
0
2/)(
,
)2/exp()2/exp(
2)2/()2/(
1
/
ˆˆ
/
ˆ
/
ˆ
}
ˆ
(
mnwz
nm
nm
mn
m
n
тn
duuuwwdw
nm
mnhzhPz
mh
nh
PzFP
Искомая плотность вероятности получается дифференцированием функции распределе-
ния по переменной z и вычисления получившегося интеграла, с помощью замены
ynzmw 2)/1(
и определения гамма-функции:
0 ,)/1(
)2/()2/(
)/)(2/)((
)(
2/)(12/
2/
,
zmznz
mn
mnmn
z
mnn
n
mn
.
В отличии от плотности гамма-распределения, плотность распределения Фишера характе-
ризуется степенным, а не экспоненциальным спадом при больших значениях переменной.
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Техника дифференцирования и интегрирования
Техника дифференцирования
Дифференцирование простая операция, - для ее правильного выполнения достаточно про-
сто следовать правилам, описанным в главе «Основные понятия» и знать небольшой базо-
вый набор производных элементарных функций. Главное при изучении дифференцирова-
ния, - это доведение выполнения данной операции до безошибочного и желательно быст-
рого выполнения, лишь безошибочное дифференцирование гарантирует успешное обуче-
ние интегрированию. В рассмотренных ниже простых примерах приводятся технические
приемы, упрощающие дифференцирование, а также некоторые простейшие задачи гео-
метрии и физики, в которых используются производные.
Элементарные приемы
Прежде чем дифференцировать, посмотрите на формулу функции. Вспомните, что диф-
ференцировать сумму проще, чем произведение, а произведение дифференцировать про-
ще, чем частное. Поэтому, по возможности перепишите исходную формулу функции в
более удобном для дифференцирования виде.
Пример 1. Вычислить производные функций
А)
)2(log
x
x
, В)
4
44
22
ln
bx
ax
, С)
2
2
1
1
x
x
, D)
1
22
xx
, E)
|)ln(| x
А) Здесь достаточно преобразовать функцию, используя свойства логарифмов
))(ln/1)ln(/1)(2ln())/(ln()(2ln())(log/())2((log
2
2
xxxxxx
x
x
.
В) Здесь следует преобразовать функцию и воспользоваться правилом дифференцирова-
ния сложной функции
44
3
22
4422
4
44
22
2
ln
4
1
lnln
bx
x
ax
x
bxax
bx
ax
С) Эту функцию лучше представить в виде произведения и воспользоваться правилами
дифференцирования произведения и сложной функции
2/322/122/122/122/122/12
2
2
)1()1()1()1())1()1((
1
1
xxxxxxxx
x
x
D) В этом случае надо дважды применить правило дифференцирования сложной функции
tyxxtx 1
22
,
)12(
2
1
1
222
xx
t
xxty
,
zxzx 1
2
1
)1(1
2
22
x
x
xzx
.
Ответ:
1
2
12
1
1
2
22
22
x
x
x
xx
xx
.
E)
.0),ln(
,0),ln(
|)ln(|
xx
xx
x
. При отрицательных значениях переменной надо применить
правило дифференцирования сложной функции. Ответ:
xx /1)|)(ln(|
.
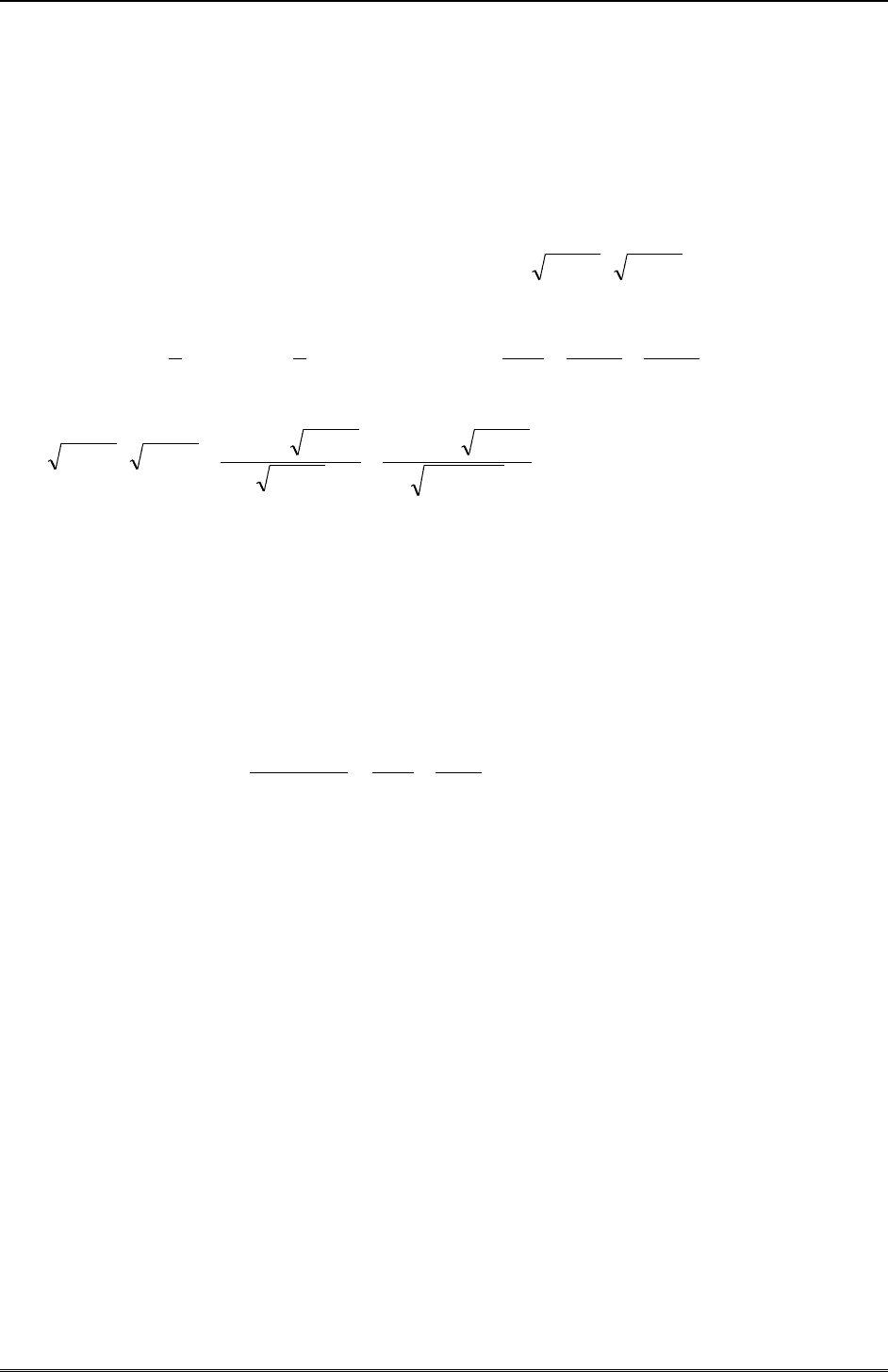
Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
2
Логарифмическое дифференцирование
Этот прием вычисления используется для сложных показательных функций
)(
)(
xw
xu
и для
функций, образованных несколькими сомножителями.
Основная идея логарифмического дифференцирования основана на предположении, что
производная логарифма функции вычисляется проще, а само вычисление основано на то-
ждестве
))((ln()()(),(/)())((ln(
xfxfxfxfxfxf
.
Пример 2. Найти производные функций А)
4
42
42)1( xxxy
, В)
2
x
xy
.
А) Найдем логарифм функции и вычислим его производную
)4ln(
4
1
)2ln(
2
1
)1ln()ln(
42
xxxy
,
4
3
2
421
1
))(ln(
x
x
x
x
x
y
.
Окончательный ответ получаем умножая производную логарифма на исходную функцию
4
34
23
2
4
4
4
42
)4(
2)1(
2
4)1(
42
x
xxx
x
xxx
xxy
.
В)
)ln()ln(
2
xxy
,
xxxxxy
)ln(2))ln(())(ln(
2
,
2
))ln(2(
x
xxxxy
.
Вычисление производных высших порядков
При вычислении производных высших порядков надо постараться получить рекуррент-
ную формулу, связывающую производные различных порядков, или преобразовать функ-
цию к наиболее удобному для вычислений виду.
Пример 3. Вычислить производную сто первого порядка функции
)23ln(
2
xxy
.
Первая производная
11
2
)2()1(
2
1
1
1
23
32
xx
xxxx
x
y
. Производные степе-
ни вычисляются тривиально: так как
1
)(
nn
xnx
, то
1)(1
!)1()(
nnn
xnx
. Оконча-
тельно получаем
))2()1((!)1())2()1((
101101)100(11)101(
xxnxxy
n
.
Пример 4. Получить формулу для производной произвольного порядка функции
)cos()exp( bxaxy
.
Воспользуемся формулой Эйлера и линейностью операции дифференцирования
))exp((Re xibay
,
))sin()(cos()Re())exp(()Re(
)(
bxibxibaxibaibay
nnn
.
Выделяя действительную часть, окончательно получаем
]2/[
0
121212
]2/[
0
222)(
)1()sin()exp()1()cos()exp(
n
k
knkkk
n
n
k
knkkk
n
n
abCbxaxabCbxaxy
.
Символ
][z
обозначает целую часть числа
z
. Аналогично можно вычислить производные
)sin()exp( bxaxy
.
Пример 5. Получить формулу Лейбница, для производных высшего порядка произведения
двух функций
n
k
knkk
n
n
xvxuCxvxu
0
)()()(
)()())()((
.

Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
3
Представим формулу дифференцирования произведения как результат действия линейно-
го оператора
)(
vu
dd
, который действует на произведение функций по следующему пра-
вилу
)()()()())()()(( xvxuxvxuxvxudd
vu
, то есть
u
d
дифференцирует только
функцию
u
, а
v
d
, - только функцию
v
. При помощи этого оператора вычисление произ-
водной произведения порядка
n
представляется как
n
-кратное применение этого опера-
тора, - степень оператора порядка
n
, то есть
n
k
knkk
n
n
k
kn
v
k
u
k
n
n
vu
n
xvxuCxvxuddCxvxuddxvxu
0
)()(
0
)(
)()())()(()()())()(()())()((
.
Применение производных в геометрии и физике
Для применения производных в физических и геометрических задачах надо четко сфор-
мулировать условие задачи на языке функций. После этого применение производной к
решению задачи становится достаточно очевидно.
Пример 6. Вода из отверстия в баке вытекает со скоростью
HgV 2
, где
H
- высота
уровня воды над отверстием. Бак заполнен водой до уровня
h
. На какой высоте от дна ба-
ка надо проделать отверстие, чтобы струя била на наибольшее расстояние?
Горизонтальная струя, направленная с высоты
y
со скоростью
V
, бьет на расстояние
gyVx /2
(почему?)
1
. Квадрат расстояния как функция вертикальной координаты от-
верстия
)(4
2
yhyx
будет максимален при
2/hy
(почему?), то есть
hx
max
.
Пример 7. Определить, где и под каким углом пересекаются параболы
2
xy
, и
2
yx
?
Параболы пересекаются в точке
)1,1(
(почему?). Угол пересечения линий, - это угол меж-
ду касательными векторами к линиям в точке пересечения. Линии в точке пересечения
можно представить графиками функций
2
xy
и
xy
. Касательные векторы к графи-
кам этих функций в точке пересечения равны
)2,1(
1
a
,
)2/1,1(
2
a
. Угол между векто-
рами вычисляется через их скалярное произведение
5/4
||||
)cos(
21
21
aa
aa
. Ответ:
)5/4arccos(
.
Пример 8. Найти угол между двумя симметричными касательными к параболе
2/
2
xy
?
Касательные проходят через точки
)2/,(
2
xx
и
)2/,(
2
xx
, а касательные векторы к пара-
боле в этих точках
),1( x
и
),1( x
. Угол между касательными
1
1
arccos
2
2
x
x
(почему?).
Пример 9. Источник тока с ЭДС
E
и внутренним сопротивлением
r
замкнут на внешнее
сопротивление
R
. Найти величину внешнего сопротивления, при которой на нем выделя-
лась максимальная мощность?
Мощность тока
2
RIW
, а ток в последовательной цепи
)/( rREI
. Следовательно,
мощность во внешней цепи
22
)(
rRREW
. Остается найти наибольшее значение этой
функции. Для этого перепишем мощность через безразмерную переменную
rRx /
:
22
)1()/(
xxrEW
, а для отыскания максимума мощности найдем положительный
1
Тонкая струя вытекающей воды, при пренебрежении силами сопротивления, имеет вид траектории точки,
движущейся в однородном поле тяготения.
Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
4
нуль производной
322
)1(2)1())1((
xxxxx
(почему?). Приравнивая производ-
ную нулю, находим
1x
, то есть мощность максимальна когда внешнее сопротивление
цепи равно внутреннему сопротивлению источника.
Техника интегрирования
Рассматривая ниже техника интегрирования используется для решения задачи аналитиче-
ского интегрирования, которая состоит в нахождении по заданной функции
)(xf
ее неоп-
ределенного интеграла
CxFdxxf
)()(
, где
)(xF
, - любая первообразная функции
)(xf
, определяемая условием
)()( xfxF
2
.
В задаче аналитического интегрирования предполагается, что формула первообразной
должна записываться только через рациональные, алгебраические и элементарные транс-
цендентные функции. Это ограничение носит принципиальный характер, так как сущест-
венно ограничивает класс функций, для которых задача аналитического интегрирования
может быть решена.
Например, для функции
xx /)sin(
задача аналитического интегрирования не решается, но
для каждого отдельного сомножителя
)sin(x
и
x/1
она может быть легко решена любым,
кто знает таблицу элементарных производных
3
.
Технику интегрирования можно, достаточно условно, разделить на элементарное интег-
рирование, и интегрирование классов функций.
Элементарное интегрирование, основано на правилах интегрирования, следующих
из правил дифференцирования, дополненных набором типичных сценариев их ис-
пользования.
Интегрирование классов функций, это набор стандартных сценариев, применение
которых к определенному классу функций всегда приводит к решению задачи ана-
литического интегрирования.
В приведенных формулировках под сценариями интегрирования понимается описание ти-
пичных действий, которые необходимо выполнить для аналитического интегрирования
функций определенного вида. Однако, сказать что техника интегрирования сводится
только к использованию известных сценариев нельзя. Часто бывает так, что для интегри-
рования одной и той же функции можно использовать несколько подходов, причем при-
менение стандартного сценария является далеко не лучшим способом решения задачи.
Поэтому, догадка и фантазия играют в аналитическом интегрировании значительную
роль. Иными словами, знание сценариев подсказывает идеи, возможные пути решения за-
дачи, но не освобождает от ответственности за выбранную реализацию интегрирования
конкретной функции.
2
Поскольку аналитическое интегрирование считается выполненным, когда найдена любая первообразная,
вместо строгой записи
CxFdxxf
)()(
, для краткости, будем писать
)()( xFdxxf
.
3
В подобных случаях формулы, содержащие интегралы использую для определения новых функций, отно-
сящихся к классу так называемых специальных функций. Возникающая в рассмотренном примере функция
называется интегральный синус
x
dz
z
z
x
0
)sin(
)Si(
,
x
x
x
)sin(
)(iS
.
Значения интегрального синуса при конкретном значении аргумента вычисляются при помощи процедуры
численного интегрирования, опирающейся на понятие определенного интеграла.

Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
5
Важно понять, что в основе каждой конкретной реализации интегрирования лежит
личный опыт, приобретаемый в ходе самостоятельного решения задач и изучения сцена-
риев, которые обобщают опыт, накопленный предшественниками.
Элементарное интегрирование
Элементарное интегрирование, - это основа техники интегрирования. Оно базируется,
главным образом, на умении распознавать первообразные подынтегральных функций, то
есть определять, а порой и угадывать, производная, какой конкретной функции стоит под
знаком интеграла. Все остальное, это набор типичных сценариев преобразования подын-
тегральных функций, облегчающих распознавание первообразных.
Для освоения элементарного интегрирования необходимо знать некоторый базовый набор
первообразных, и научиться читать формулы дифференцирования справа налево. Это
служит первоосновой интегрирования. Чем шире базовый набор первообразных, тем лег-
че осуществить выбор подходящего сценария интегрирования. В качестве базового набо-
ра первообразных можно использовать элементарные интегралы, приведенные таблице 1.
Таблица 1 Формулы производных и интегралов простейших элементарных функций
Дифференцирование
Интегрирование
1
)(
aa
axx
1 ),1/(
1
aaxdxx
aa
xx /1)(nl
( / ) ln(| |)1 x dx x
)exp())(exp( axaax
exp( ) ( / ) exp( )ax dx a ax
1
)cos()(nsi axaax
)sin()/1()cos( axadxax
)sin()(sco axaax
sin( ) ( / ) cos( )ax dx a ax
1
)(cos/1)(gt
2
xx
)tg())(cos/1(
2
xdxx
)(sin/1)(gct
2
xx
)ctg())(sin/1(
2
xdxx
2
1/1)(narcsi xx
,
2
1/1)(sarcco xx
( / ) arcsin( )1 1
2
x dx x
)1/(1)(garct
2
xx
,
)1/(1)(garcct
2
xx
)arctg())1/(1(
2
xdxx
)ch()(hs axaax
)sh()/1()ch( axadxax
)sh()(hc axaax
)ch()/1()sh( axadxax
)(/ch1)(ht
2
xx
)th())(ch/1(
2
xdxx
)(/sh1)(hct
2
xx
)cth())(/sh1(
2
xdxx
2
1/1)(hArs xx
)1ln()1/1(
22
xxdxx
