Алексеев Д.В. Конспекты по общему курсу математики
Подождите немного. Документ загружается.


Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
6
1/1)(hArc
2
xx
)1ln()1/1(
22
xxdxx
Задача. Внимательно просмотрите все строки таблицы 1 и проследите, как при помощи
дифференцирования первообразной получается подынтегральная функция.
Простейшая идея интегрирования состоит в сведении исходного интеграла к одному или
нескольким известным интегралам при помощи правил интегрирования, следующих не-
посредственно из правил дифференцирования (таблица 2).
Таблица 2 Сопоставление основных правил дифференцирования и интегрирования.
Дифференцирование
Интегрирование
Линейность
)()())()(( xgBxfAxgBxfA
Линейность
dxxgBdxxfAdxxgBxfA )()())()((
Дифференцирование
произведения
)()()()())()(( xgxfxgxfxgxf
Формула интегрирования произведения
(интегрирование «по частям»)
dxxgxfdxxgxfxgxf )()()()()()(
Дифференцирование
сложной функции
)()()))((( xfxf
Интегрирование подстановкой
(«подведение под дифференциал»)
))(()())(()()( xFdxxxfxFdxxf
Применение правил интегрирования позволяет сделать следующие преобразования:
Свойство линейности позволяет разбить исходный интеграл на сумму нескольких
более простых, а точнее, более знакомых интегралов.
Формула интегрирования подстановкой позволяет выписывать первообразные для
производных сложных функций.
Формула интегрирования произведения позволяет преобразовывать исходные ин-
тегралы к более простым интегралам, при помощи подходящего выбора функций-
сомножителей.
Критерием правильности выбора конкретной идеи преобразования подынтегральной
функции, или сценария интегрирования, служит упрощение исходного интеграла в ходе
преобразования. Если после преобразований исходный интеграл усложняется, надо, ско-
рее всего, применить другой способ.
Таким образом, техника элементарного интегрирования базируется на основных правилах
интегрирования (таблица 2), базовом наборе первообразных (таблица 1) и типичных сце-
нариях интегрирования функций различных типов.
Научиться интегрировать, - значит приобрести собственный опыт в ходе изучения ти-
пичных сценариев интегрирования, - опыта предшественников, и самостоятельного ре-
шения конкретных задач.
Применение линейности
Применение линейности основано на тождественных преобразованиях подынтегральной
функции, конкретный вид которых зависит от рассматриваемой функции. Например, для
преобразования тригонометрических функций могут использоваться разнообразные три-
гонометрические тождества, а для преобразования алгебраических функций, - формулы
сокращенного умножения. В приводимых ниже примерах показано, как можно сводить
исходный интеграл к интегралам из базового набора

Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
7
Пример 1.
dx
x
dx
x
dx
xx
xx
dx
x
xx
1
1
1
1
)1)(1(
11
1
11
2222
22
4
22
.
Пример 2.
dxxdx
x
dx
x
xx
dx
x
xx
dx
x
xx
5
3
22
3
222
3
44
1
)(
2
.
Пример 3.
dx
x
dx
x
dx
xx
xx
dx
xx )(sin
1
)(cos
1
)(cos)(sin
)(cos)(sin
)(cos)(sin
1
2222
22
22
.
Пример 4.
||ln
1
||ln
1111
))((
1
bx
ba
ax
ba
dx
bxaxba
dx
bxax
.
Приведенные примеры демонстрируют лишь идею использования линейности. Все ос-
тальное будет зависеть от конкретной функции и вашего личного опыта проведения тож-
дественных преобразований.
Применение формулы интегрирования произведения
Формула интегрирования произведения применяется для преобразования исходного инте-
грала в следующем виде
dxxgxfxgxfdxxgxf )()()()()()(
.
Для применения этой формулы необходимо путем самостоятельного выбора разложить
подынтегральную функцию на два сомножителя, один из которых
)(xf
, а другой, -
)(xg
.
Если выбор сделан удачно, то интеграл, возникающий в правой части будет проще исход-
ного интеграла. Приводимые ниже примеры демонстрируют некоторые типичные сцена-
рии выбора разложения подынтегральной функции на сомножители.
Сценарий 1. Один из сомножителей является обратной трансцендентной функцией.
Пример 1.
xxxdxxxxxdxxxdxx
)ln())(ln()ln()ln()()ln(
.
Задача. Проведите подобные вычисления для интегралов
dxx)arcsin(
,
dxx)arctg(
.
В случаях, когда для достижения результата формулу интегрирования произведения при-
ходится применить несколько раз, промежуточный результат удобно выписывать с помо-
щью рекуррентных формул, связывающих однотипные интегралы.
Сценарий 2. Подынтегральная функция является произведением степени с натуральным
показателем и элементарной трансцендентной функции.
Пример 2. Рассмотреть интегралы вида
dxaxxaS
n
n
)sin()(
,
dxaxxaC
n
n
)cos()(
.
Стартовые интегралы
)(),(
00
aCaS
входят в перечень элементарных интегралов. Для дру-
гих натуральных значений показателя степени получаем
dxaxx
a
n
ax
a
x
dxax
a
xdxaxxaS
n
n
nn
n
)cos()cos())cos(
1
()sin()(
1
,
dxaxx
a
n
ax
a
x
dxax
a
xdxaxxaC
n
n
nn
n
)sin()sin())sin(
1
()cos()(
1
.
В эти формулы входят интегралы
)(),(
11
aCaS
nn
. Окончательный результат записывается
в виде пары рекуррентных формул

Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
8
)()cos()(
1
aC
a
n
ax
a
x
aS
n
n
n
,
)()sin()(
1
aS
a
n
ax
a
x
aC
n
n
n
.
Спускаясь при помощи этих формул вниз как по лестнице, легко добраться до опорных
интегралов
)(),(
00
aCaS
.
Задача. Получите рекуррентную формулу для интеграла
dxaxxaE
n
n
)exp()(
.
Пример 3. Рекуррентная формула для рационального интеграла
dx
ax
aI
n
n
)(
1
)(
22
.
Стартовым интегралом является
)/arctg(
11
)(
22
1
ax
a
dx
ax
aI
.
При
1n
, преобразуем интеграл к виду
dx
n
ax
x
aa
aI
dx
ax
x
aa
aI
dx
ax
xax
a
aI
n
n
n
n
n
n
)1(2
))((1)(
)(
1)(
)(
1
)(
)1(22
22
1
22
2
22
1
22
222
2
.
Интеграл в правой части последнего равенства вычисляется при помощи формулы интег-
рирования произведения
)(
)1(2
1
)()1(2
1
)1(2
))((
1
122
)1(22
aI
nax
x
n
dx
n
ax
x
n
n
n
.
Подстановка этого результата в предыдущую формулу окончательно дает
1222
1
222
)()22(
1
)(
)22(
32
)(
1
)(
n
n
n
n
ax
x
na
aI
na
n
dx
ax
aI
.
Эта рекуррентная формула применяется при интегрировании рациональных дробей.
Задача. Вычислите при помощи рекуррентной формулы
dx
x
42
)4(
1
.
Сценарий 3. Повторное применение формулы интегрирования произведения приводит к
уравнению относительно исходного интеграла.
Пример 4. Вычислить интеграл
dxxaxJ )sin()exp(
. Дважды применяем формулу интег-
рирования произведения, получаем
dxxaxaxaxdxxaxdxxax )cos()exp()cos()exp())cos()(exp()sin()exp(
,
dxxaxaxaxdxxaxdxxax )sin()exp()sin()exp()))(sin(exp()cos()exp(
.
Объединяя данные формулы, получаем уравнение для исходного интеграла
JaxaxaxaxJ
2
)sin()exp()cos()exp(
. Ответ:
2
1
))sin()cos()(exp(
a
xaxax
J
.
4
4
Для тех, кто знаком с комплексными числами и формулой Эйлера
)sin()cos()exp( xixix
полезно
знать и другой путь, обходящийся без формулы интегрирования произведения
ia
ixax
dxixaxdxxax
)exp()exp(
Im)exp()exp(Im)sin()exp(
.

Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
9
Преобразование интегралов заменами переменной
Преобразование интегралов заменами переменной, едва ли не самый главный технический
прием, применяемый в аналитическом интегрировании. Этот технический прием можно
подразделить на следующие две разновидности
Прямая подстановка (подведение под дифференциал)
Замена переменной (преобразование подынтегральной функции)
Для прямой подстановки необходимо увидеть в формуле подынтегральной функции
структуру производной сложной функции. Именно увидеть, что способен сделать только
человек, свободно владеющий техникой дифференцирования сложных функций. В этом
случае напрямую применяется формула из таблицы 2
))(()())(()()( xFdxxxfxFdxxf
.
Для замены переменной используется стандартная формула для дифференциала функции
вспомогательной переменной
dttutufdxxfdttudxtux )())(()()()(
.
При этом критерием правильности выбора функции для замены переменной служит то,
что подынтегральная функция новой переменной
)())(( tutuf
является более простой, чем
исходная подынтегральная функция
)(xf
.
Сценарий 1. Линейные замены переменных
baxt
.
Этот простой метод интегрирования должен быть отработан до автоматизма.
Пример 1. Интеграл
dxa
x
часто вносят в таблицу базовых интегралов. Однако, проще
выразить показательную функцию через стандартную экспоненту
))ln(exp( axa
x
.
Тогда
)ln(
))ln(exp(
)ln(
1
))ln(exp(
a
a
ax
a
dxaxdxa
x
x
.
Пример 2.
)cos(
1
)cos(
1
)sin(
1
,
)sin(
txdxx
dtdx
tx
dtt
.
Задача. Опираясь на элементарные интегралы таблицы 1, напишите 8 – 10 примеров ин-
тегрирования при помощи линейных замен переменной.
Сценарий 2. Интегралы от произведений тригонометрических функций.
Пример 3. Интегралы вида
dxxx
mn
)(cos)(sin
122
,
dxxx
mn
)(cos)(sin
212
преобразуют, ис-
пользуя дифференциалы синуса или косинуса
dxxxd )cos()sin(
,
dxxxd )sin()cos(
, а
также основное тригонометрическое тождество. В результате замены переменной эти ин-
тегралы превращаются в интегралы от многочленов:
dzzz
zx
dzdxx
zx
dxxx
mnmn
)1(
1)(cos
,)cos(
,)sin(
)(cos)(sin
22
22
122
,
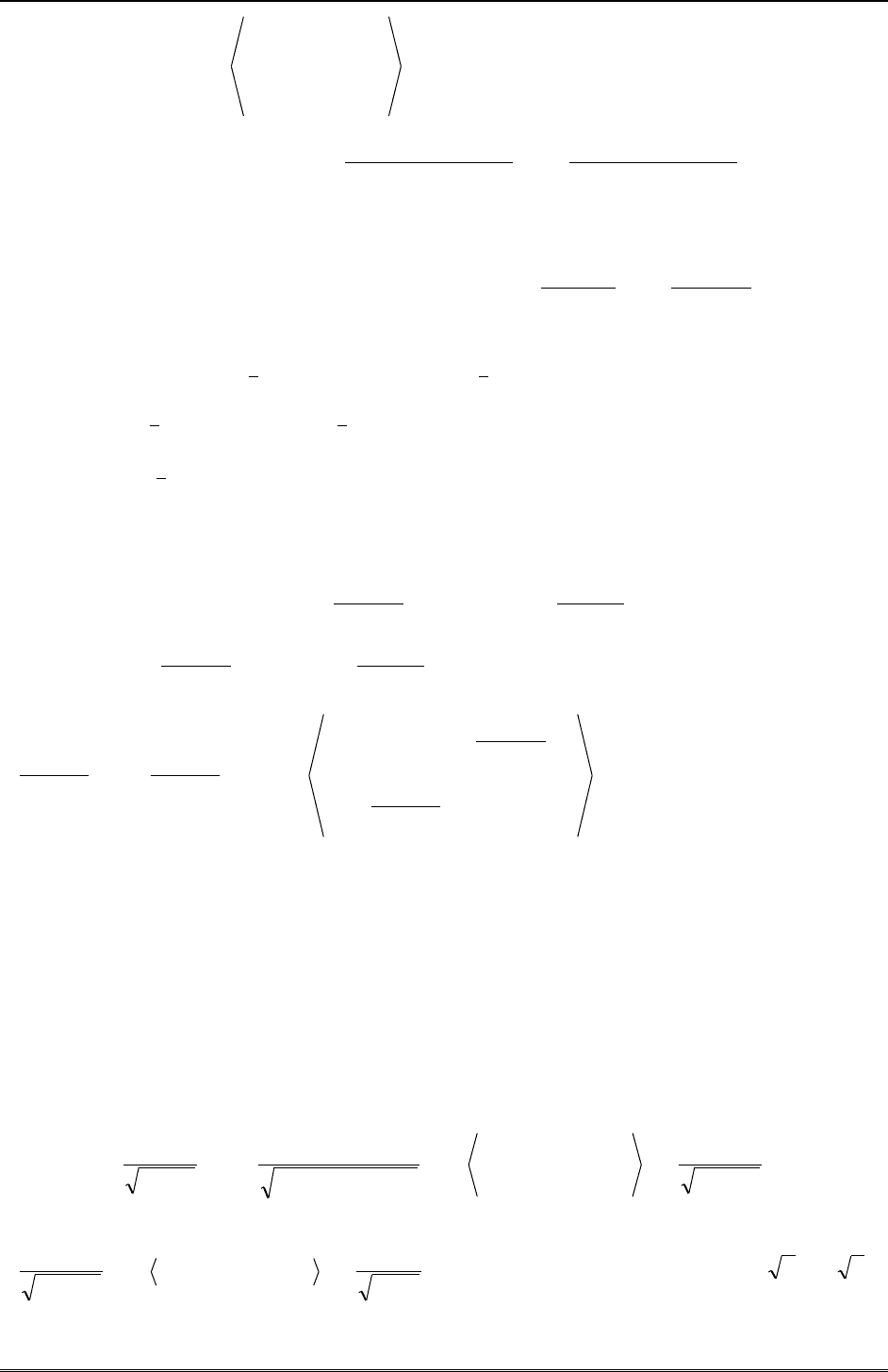
Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
10
dzzz
zx
dzdxx
zx
dxxx
mnmn 22
22
212
)1(
1)(sin
,)sin(
,)cos(
)(cos)(sin
.
Задача. Преобразуйте интегралы
dx
xx
mn
)(cos)(sin
1
122
,
dx
xx
mn
)(cos)(sin
1
212
к интегра-
лам от рациональных дробей при помощи умножения числителя и знаменателя на синус
или косинус с последующей заменой переменной.
Пример 4. Интегралы вида
dxx
n
)(sin
2
,
dxx
m
)(cos
2
,
dx
x
n
)(sin
1
2
,
dx
x
m
)(cos
1
2
.
Интеграл от положительной четной степени преобразуют при помощи формул перехода к
кратным углам
))2cos(1()(cos
2
1
2
xx
,
))2cos(1()(sin
2
1
2
xx
, например,
dxxxdxxdxx ))2(cos)2cos(21()))2cos(1(()(sin
2
4
1
2
2
1
4
,
dxxdxx ))4cos(1()2(cos
2
1
2
.
Для завершения вычислений используется линейность и линейные замены переменных.
В интегралах от отрицательных четных степеней используют формулы дифференциалов
тангенса или котангенса
dx
x
xd
)(cos
1
)tg(
2
,
dx
x
xd
)(sin
1
)ctg(
2
и тригонометрические
тождества типа
)(tg1
)(cos
1
2
2
x
x
,
)(ctg1
)(sin
1
2
2
x
x
. Например,
dzz
z
x
dx
x
dzzx
xd
x
dx
x
22
2
2
2
46
)1(
1
)(cos
1
,
)(cos
1
,)tg(
)tg(
)(cos
1
)(cos
1
.
В более сложных случаях используют одну из изложенных идей, которая больше подхо-
дит к конкретной интегрируемой функции. Аналогичные идеи используются для интегри-
рования произведений гиперболических функций. Отличие состоит лишь в том, что пре-
образования проводятся при помощи тождеств для гиперболических функций.
Сценарий 3. Выделение полного квадрата.
Интегралы, содержащие квадратичную функцию, часто преобразуют при помощи выде-
ления полного квадрата, для чего можно воспользоваться формулой
abcabxacbxax 4/)2/(
222
,
abxz 2/
. Однако, проще это делать простым
подбором.
Пример 5.
dz
za
adxdz
xz
dx
x
dx
xx
22
2
22
1
4/1,
,2/1
)2/1(4/1
11
.
Далее еще одна линейная замена
)2/12arcsin()/arcsin()arcsin(
1
1
,
1
222
xaztdt
t
adtdzatzdz
za
.

Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
11
Пример 6.
dz
az
adxdz
xz
dx
x
dx
xx
22
2
22
1
4/1,
,2/1
4/1)2/1(
11
,
Затем дробь разбивают на сумму простейших дробей, используют линейность и линейные
замены переменных
||ln
2
1
||ln
2
111
2
1
))((
11
22
az
a
az
a
dz
azaza
dz
azaz
dz
az
.
Выписать окончательный ответ не составляет труда.
Чаще всего, при аналитическом интегрировании приходится комбинировать рассмотрен-
ные выше сценарии различными способами. Как это следует делать, зависит от конкрет-
ного вида подынтегральной функции и личного опыта человека, решающего задачу.
Интегрирование некоторых классов функций
Интегрирование классов функций, - это набор стандартных сценариев, основой которых
является техника интегрирование рациональных дробей. Главный результат об интегри-
ровании рациональных дробей формулируется следующим образом:
Интеграл от любой рациональной функции выражается через рациональные функции,
логарифмы и арктангенсы.
Все остальное, - это сведение исходного интеграла к рациональной дроби при помощи
стандартной замены переменной. Следует помнить: использование стандартного сцена-
рия, - это последнее средство, применяемое лишь тогда, когда не удается найти более
короткого пути интегрирования конкретной функции.
Интегрирование рациональных дробей
Функция называется рациональной дробью, если она представляется в виде
)(/)( xPxP
mn
,
где
)(),( xPxP
mn
, - многочлены, старшая степень которых указывается индексом.
Если старшая степень знаменателя больше старшей степени числителя, дробь называется
правильной. В противном случае дробь называется неправильной.
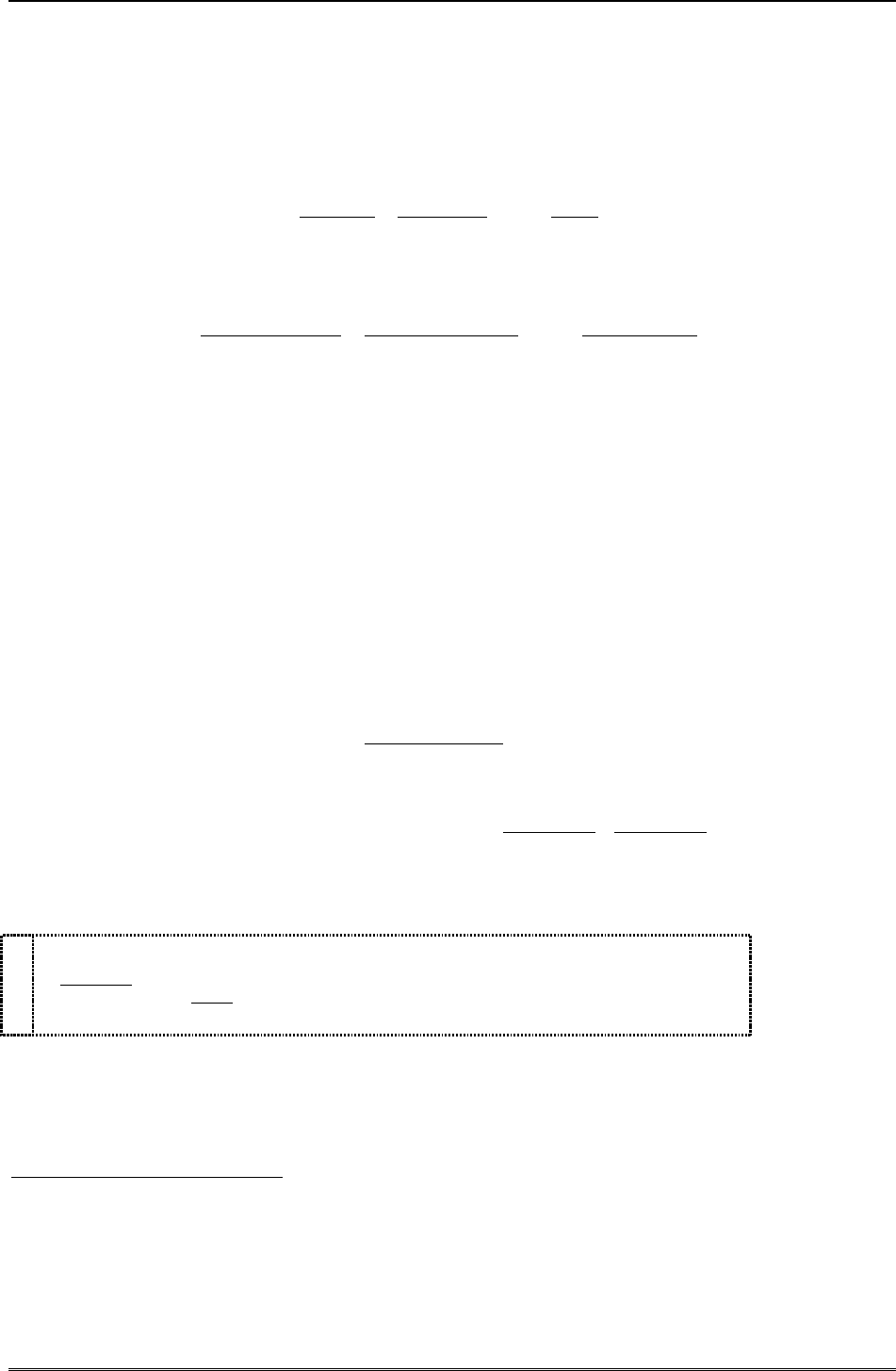
Неправильную дробь можно разбить путем деления на сумму целой части, - многочлена, и
правильной дроби:
mp
xP
xR
xQ
xP
xP
mn
m
p
mn
m
n
,
)(
)(
)(
)(
)(
.
В выписанном представлении рациональной функции многочлены
)(xQ
и
)(xR
называ-
ются частным и остатком соответственно.
Многочлен интегрируется тривиально, при помощи свойства линейности. Нетривиальная
часть задачи интегрирования рациональной функции связана с интегрированием правиль-
ной дроби. В основе интегрирования рациональных дробей лежит представление пра-
вильной рациональной дроби в виде суммы так называемых элементарных дробей.
Опишем систематическую процедуру разложения правильной дроби в сумму элементар-
ных дробей, называемую метод неопределенных коэффициентов. Эта процедура начина-
ется с разложения знаменателя исходной дроби в произведение элементарных сомножите-
Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
12
лей, в основе которого лежит основная теорема алгебры.
5
В интересующем нас случае
многочленов с вещественными коэффициентами, основная теорема алгебры гарантирует
разложение многочлена в произведение вещественных линейных сомножителей и квадра-
тичных сомножителей с отрицательными дискриминантами (среди сомножителей могут
встречаться одинаковые, что соответствует кратным корням). Линейным сомножителям
m
ax )(
сопоставляется серия элементарных дробей
ax
A
ax
A
ax
A
m
m
m
m
1
1
1
)()(
,
а квадратичным сомножителям
k
qpxx )2(
2
, - серия элементарных дробей
qpxx
CxB
qpxx
CxB
qpxx
CxB
k
kk
k
kk
2)2()2(
2
11
12
11
2
.
Входящие в числители данных дробей константы называются неопределенными коэффи-
циентами, так как их значения подлежать дальнейшему определению. Полно число неоп-
ределенных коэффициентов в точности равно старшей степени знаменателя, что находит-
ся в полном соответствии с тем, что разлагаемая в сумму дробь является правильной.
6
Для вычисления неопределенных коэффициентов выписанную с их помощью сумму эле-
ментарных дробей приводят к общему знаменателю, приравнивают полученный числи-
тель числителю исходной дроби и из условия равенства многочленов составляют систему
линейных уравнений для неопределенных коэффициентов. Решение полученной системы
завершает нахождение коэффициентов, входящих в разложение правильной дроби в сум-
му элементарных дробей.
Разложение правильной дроби в сумму элементарных дробей принципиально важно по-
тому, что интеграл от любой элементарной дроби может быть выражен через элементар-
ные функции. При этом дроби вида
n
qpxx
CBx
)2(
2
следует привести к простейшему виду
при помощи выделения полного квадрата и линейной замены переменной, то есть перепи-
сать их в виде линейной комбинации дробей вида
n
ax
x
)(
22
,
n
ax )(
1
22
. Все интегралы от
элементарных дробей перечислены в таблице 3.
Таблица 3 Интегралы от элементарных дробей.
1
1,)(
1
1
1|),ln(|
)(
1
1
nax
n
nax
dx
ax
n
n
5
Основная теорема алгебры гласит: Любой многочлен степени
n
может быть разложен в произведение ли-
нейных сомножителей
j
k
jn
axxP )()(
, где
j
a
корни (нули) многочлена ( в общем случае ком-
плексные), а
j
k
их кратности, удовлетворяющие условию
nk
j
.
6
Многочлен
01
1
1
axaxaxa
n
n
n
n
полностью определяется
1n
коэффициентами. Значит у
правильной дроби старшая степень числителя, в общем случае, на единицу меньше старшей степени знаме-
нателя, что и определяет полное число неопределенных коэффициентов.

Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
13
2
1,)(
)1(2
1
1),ln(
2
1
)(
122
22
22
nax
n
nax
dx
ax
x
n
n
3
1,
)()22(
1
)(
)22(
32
)(
1
)(
1222
1
222
n
ax
x
na
aI
na
n
dx
ax
aI
n
n
n
n
)/arctg(
11
)(
22
1
ax
a
dx
ax
aI
Описанный выше метод неопределенных коэффициентов гарантирует разложение любой
правильной дроби в сумму элементарных дробей. Однако, ввиду громоздкости, метод не-
определенных коэффициентов следует применять только в крайних случаях, когда не уда-
ется найти более простого пути представления конкретной рассматриваемой рациональ-
ной дроби в виде суммы элементарных дробей.
В рассматриваемых ниже примерах приводятся некоторые приемы, упрощающие разло-
жение конкретной рациональной функции в сумму элементарных дробей. При этом изло-
жение рассматриваемой задачи будет завершаться на разложении подынтегральной функ-
ции в сумму элементарных дробей. Остальные элементарные действия, - выделение пол-
ных квадратов, замены переменных и выписывание интегралов от элементарных дробей,
предлагается выполнить самостоятельно.
Пример 1.
dx
x
x
100
3
)1(
. Перспектива приводить к общему знаменателю сто дробей сразу
заставляет задуматься о поиске иного пути. Например,
99
2
100100
2
100
3
100
3
)1(
1
)1(
1
)1(
1)1)(1(
)1(
1)1(
)1(
x
xx
xx
xxx
x
x
x
x
,
979899989999
2
99
2
)1(
1
)1(
3
)1(
3
)1(
3)1(
)1(
3
)1(
3)1()1(
)1(
1
xxxx
x
xx
xx
x
xx
.
Остается выписать интеграл
dx
xxxx
979899100
)1(
1
)1(
3
)1(
3
)1(
1
.
Другой способ решения еще короче, - делаем замену переменной
1 xz
. Тогда:
dzzzzzdz
z
z
dx
x
x
)33(
)1(
)1(
979899100
100
3
100
3
.
Пример 2.
dx
x 1
1
4
. Здесь также проще использовать особенности подынтегральной
функции и известную формулу сокращенного умножения
1
2/1
1
4/1
1
4/1
1
1
1
1
1
1
2
1
2
1
1
1
1
1
2
1
1
1
22224
xxxxxxxxx
.
Пример 3.
dx
x
4
1
1
. В данном случае для разложения подынтегральной функции в сум-
му элементарных дробей придется использовать метод неопределенных коэффициентов.
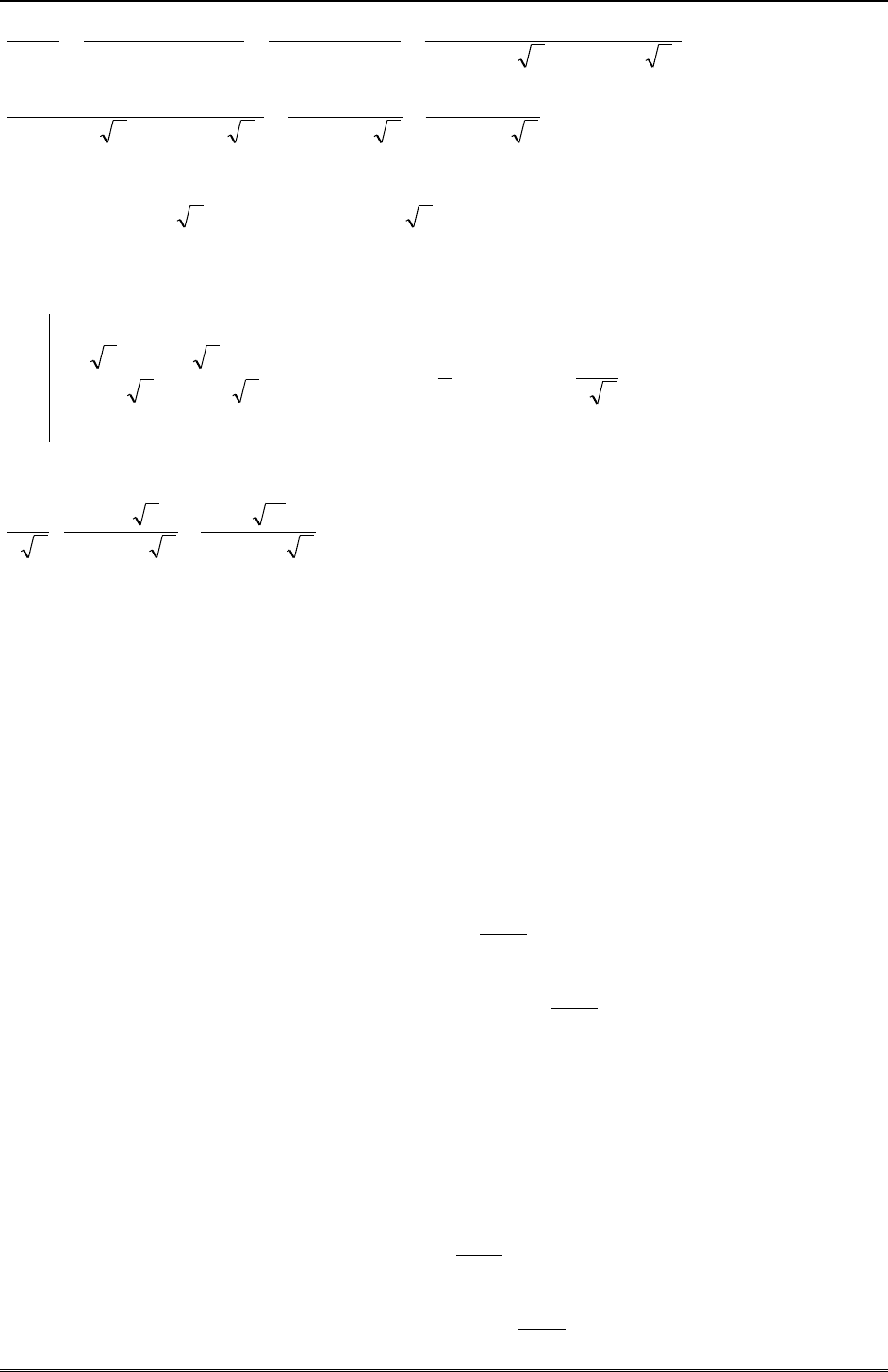
Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
14
)21)(21(
1
2)1(
1
212
1
1
1
22
2222244
xxxx
xxxxxx
,
2121)21)(21(
1
2222
xx
DCx
xx
BAx
xxxx
.
Приводя дроби к общему знаменателю и приравнивая числители, получаем
1)21)(()21)((
22
xxDCxxxBAx
.
Приравнивая коэффициенты многочленов при одинаковых степенях переменной в обеих
частях равенства, получаем систему линейных уравнений
.
22
1
,
2
1
1
022
022
0
0
1
2
3
CADB
DB
DCBA
DCBA
CA
x
x
x
x
Окончательно искомое разложение записывается в виде
21
2
21
2
22
1
22
xx
Dx
xx
x
.
Сведение к интегрированию рациональных дробей
Здесь перечислены некоторые стандартные замены переменных, которые позволяют све-
сти интегрирование рассматриваемой функции к интегрированию рациональной дроби.
Для обозначения рассматриваемых ниже функций используется символ
),,( wuR
, обо-
значающий рациональную дробь от переменных, записанных в скобках.
Еще раз напоминаем: к приводимым ниже сценариям необходимо прибегать только в
крайних случаях, когда не удалось найти более простого пути решения задачи.
Сценарий 1. Интегралы вида
dxxxR ))cos(),(sin(
.
Универсальная замена
)2/tg(xt
, совместно с тождествами
2
2
1
2
)2/(cos)2/tg(2)2/cos()2/sin(2)sin(
t
t
xxxxx
,
2
2
2222
1
1
))2/(tg1)(2/(cos)2/(sin)2/(cos)cos(
t
t
xxxxx
,
превращает исходный интеграл в интеграл от рациональной дроби.
Сценарий 2. Интегралы вида
dxxxR ))ch(),(sh(
.
Универсальная замена
)2/h(t xt
, совместно с тождествами
1)(sh)(ch
22
xx
,
)(sh)(ch)2ch(
22
xxx
,
)sh()ch(2)2sh( xxx
,
2
2
1
2
)2/(ch)2/th(2)2/ch()2/sh(2)sh(
t
t
xxxxx
,
2
2
2222
1
1
))2/(th1)(2/(ch)2/(sh)2/(ch)ch(
t
t
xxxxx
,
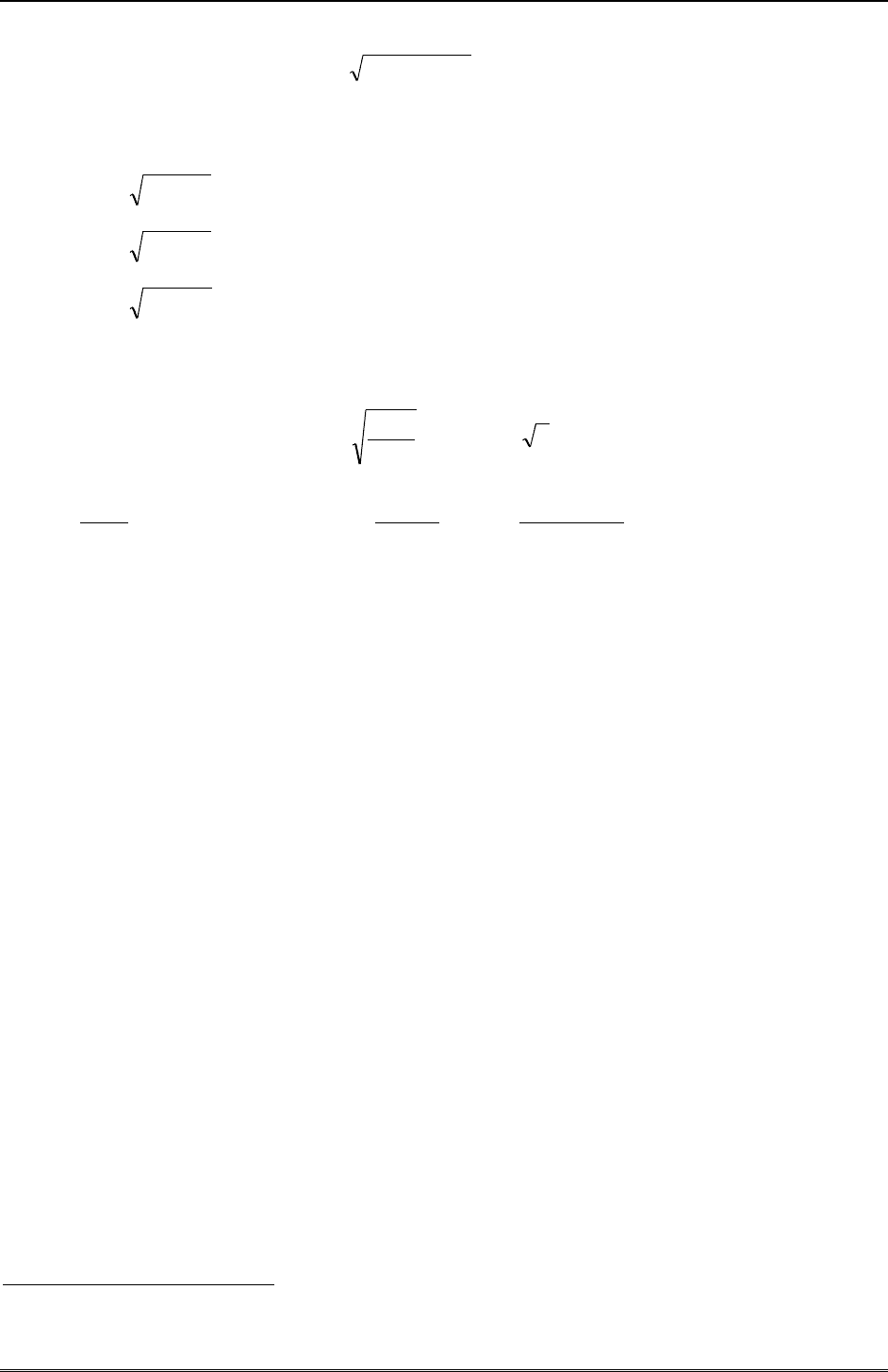
Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
15
превращает исходный интеграл в интеграл от рациональной дроби.
Сценарий 3. Интегралы вида
dxcbxaxxR ),(
2
.
Вначале следует преобразовать подынтегральную функцию путем выделения полного
квадрата. В результате исходный интеграл переходит в один из следующих типов
1.
dzzpzR ),(
22
,
)sin(tpz
,
2.
dzpzzR ),(
22
,
)sin(/ tpz
,
3.
dzpzzR ),(
22
,
)tg(tpz
Стандартные замены переменной, указанные рядом с каждым из этих типов интегралов,
сводят их к интегралам от тригонометрических функций.
7
Сценарий 4. Интегралы вида
dx
bx
ax
xR
n
,
,
dxxxR
n
,
.
Замена
n
t
bx
ax
и ее следствия
1
n
n
t
abt
x
,
dt
t
ntba
dx
n
n
2
1
)1(
)(
, сводит первый инте-
грал к интегралу от рациональной дроби. Со вторым интегралом еще проще
n
tx
,
dtntdx
n 1
. Если в формуле подынтегральной функции встречается несколько радикалов,
показатель степени следует подобрать так, чтобы все дробные показатели степени в ко-
нечной формуле исчезли.
О таблицах интегралов
Приведенные выше сценарии интегрирования, особенно сценарии замены переменных,
надо уметь использовать для сведения заданных интегралов, к интегралам приводимым в
различных справочных таблицах. В качестве таковых укажем лишь четыре наиболее рас-
пространенных источника:
1. Градштейн М. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений.
– М., Наука, 1971.
2. Двайт Г. Б. Таблицы интегралов и другие математические формулы. – М., Наука,
1977.
3. Прудников А. П., Брычков Ю. А., Маричев О. И. Интегралы и ряды. Элементарные
функции. – М., Наука, 2003.
4. Прудников А. П., Брычков Ю. А., Маричев О. И. Интегралы и ряды. Специальные
функции. – М., Наука, 2003.
Настоятельно рекомендуется научиться пользоваться приведенными здесь, или другими
подобными справочными таблицами.
Умение пользоваться таблицами интегралов принципиально важно потому, что в них све-
дены не только интегралы, первообразные которых выражаются через элементарные
функции, но и приводится большое число формул для интегралов, выражающихся через
7
Для тех, кто предпочитает работать с гиперболическими функциями, укажем, что интегралы под номера-
ми, 2 и 3 заменами
)ch(tpz
и
)sh(tpz
, соответственно сводятся к интегралам от гиперболических
функций, которые вычисляются подобно тригонометрическим интегралам.
