Алексеев Д.В. Конспекты по общему курсу математики
Подождите немного. Документ загружается.


7
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Проверка гипотезы о законе распределения
Для проверки гипотезы о законе распределения результатов измерений используется
представление выборки в сгруппированном виде, называемом гистограммой. Это пред-
ставление данных строится следующим образом:
Выбирается тестируемый (гипотетический) закон распределения (в рассматривае-
мом случае базовой модели это нормальное распределение
N x S( , )
2
с парамет-
рами, оцененными по исходной выборке).
Интервал допустимых значений случайной величины разбивается на несколько ин-
тервалов, - «карманов».
Подсчитываются «наблюдаемые частоты», - число элементов выборки, попадаю-
щих в каждый из карманов.
На основе тестируемого закона распределения вычисляются «расчетные часто-
ты», - число элементов выборки, попадающих в каждый карман.
Проводится сравнение наблюдаемых и расчетных частот.
Сгруппированные данные выборки наглядно представляются в виде системы прямоуголь-
ников, ступенчатой фигуры, называемой гистограммой. Ширина основания отдельного
прямоугольника равна ширине кармана, а его площадь, - частоте попаданий данных в
карман (наблюдаемой или расчетной).
Проблема выбора числа карманов и их ширины является достаточно нетривиальной. Не-
правильный выбор карманов может полностью обесценить результаты статистического
сравнения расчетных и наблюдаемых частот.
Для нормального распределения, и других распределений непрерывных и неограничен-
ных случайных величин, карманы выбирают на основе рекомендаций У. Кокрена:
Число карманов определяется объемом выборки по правилу
nm
,
Границы крайних карманов (для распределений неограниченных случайных вели-
чин) определяются условием: «расчетная частота попадания в крайний карман
равна единице»,
Все остальные карманы имеют равную ширину.
Перечисленные рекомендации опираются на большой опыт практического тестирования
гипотез о законе распределения.
Статистический критерий сравнения наблюдаемых и расчетных частот опирается на рас-
смотрение случайной величины
m
k
k
kk
np
npn
1
2
2
ˆ
ˆ
,
которая характеризует суммарное квадратичное отклонение наблюдаемых частот
n
k
от
расчетных частот
nnp
k
(
p F a F a
k k k
( ) ( )
1
, - вероятность попадания элемента вы-
борки в карман с границами
kk
aa ,
1
, рассчитываемая по функции распределения тести-
руемого закона). В частности, для нормального распределения левая граница крайнего ле-
вого кармана равна
, а правая граница крайнего правого кармана, -
.
Случайные величины
n
k
описывают число попаданий элементов выборки в k-й карман.
Из
m
случайных величин
n
k
только
1 sp
являются независимыми, что обусловлено
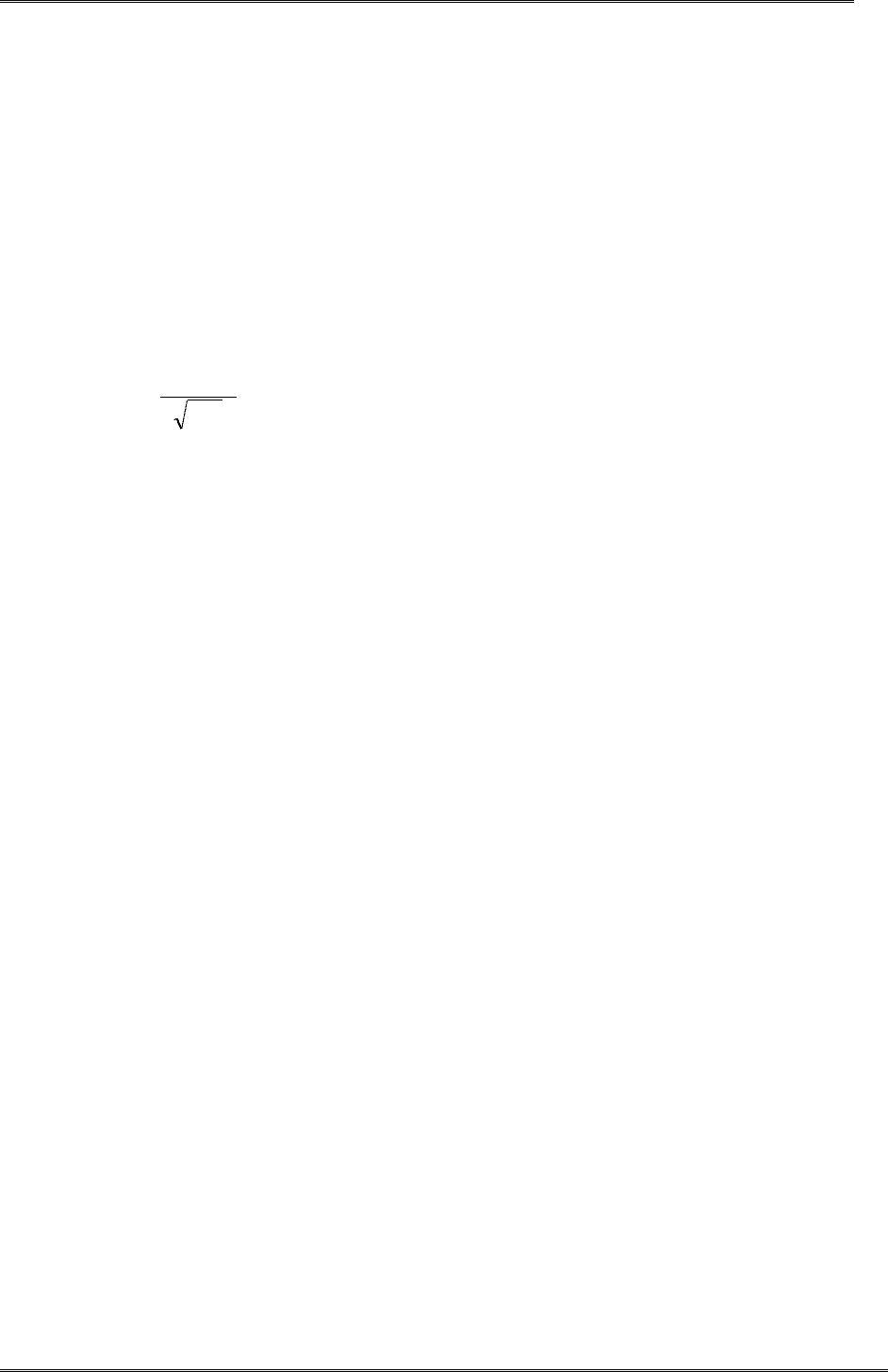
8
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
наложением на них
1s
связи. Одна из связей обусловлена фиксированным объемом вы-
борки
nn
P
k
k
1
ˆ
, а другие тем, что границы карманов вычисляются по
s
параметрам тес-
тируемого закона распределения (для нормального распределения
2s
).
Статистиком К. Пирсоном было установлено, что рассматриваемая случайная величина
2
приближенно имеет распределение
- квадрат с
1 sp
степенями свободы (поэтому
данную случайную величину называют
- квадрат расстоянием Пирсона).
Статистическое правило сравнения наблюдаемых частот с расчетными частотами строит-
ся следующим образом:
По исходной выборке вычисляется наблюдаемое значение
-квадрат расстояния
Пирсона
m
k
k
kk
B
np
npn
1
2
2
,
По найденному значению
2
B
вычисляется уровень значимости нулевой гипотезы
«тестируемое распределение описывает данные» по формуле
)
ˆ
(
22
1 Bsp
PSL
.
Уровень значимости равен вероятности получения в других реализациях рассматриваемо-
го эксперимента значений
2
1
ˆ
sp
, превосходящих значение
2
B
, вычисленное по исходной
выборке. Если уровень значимости достаточно велик, то нулевая гипотеза принимается
(отметим, что идеальное совпадение наблюдаемых частот с расчетными частотами дает
0
2
B
и соответствует уровню значимости 100%).
Смысл выражения «уровень значимости
)
ˆ
(
22
1 Bsp
PSL
достаточно велик», определя-
ется исследователем на основе критериев и требований, являющихся стандартом в той об-
ласти знаний, к которой относятся анализируемые данные.
Измерение линейной зависимости на фоне нормального шума
(элементы метода наименьших квадратов)
Рассматривается задача об определении коэффициентов линейной зависимости
baxy
.
Предполагается, что значения переменной
x
определяется точно, а результаты измерений
переменной
y
подвержены влиянию неконтролируемых статистически независимых слу-
чайных шумов
z
i
, имеющих одинаковое нормальное распределение
),0(
N
. Иными сло-
вами, проводится измерение набора случайных величин:
))
ˆ
;();
ˆ
;();
ˆ
;((
2211 nn
yxyxyx
, где
nizbaxy
iii
,,2,1 ,
ˆ
ˆ
,
и требуется по полученной выборке пар значений
));();;();;((
2211 nn
yxyxyx
оценить неиз-
вестные коэффициенты линейной зависимости
a
и
b
, а также проверить все остальные
гипотезы, лежащие в основе модели, а именно:
шумы имеют нормальное распределение
),0(
N
,
шумы в различных измерениях являются независимыми.

9
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Для оценки коэффициентов линейной зависимости используется минимизация суммы
квадратов отклонений наблюдаемых значений переменной
y
i
от расчетных значений
bax
i
:
n
i
ii
ybaxbaQ
1
2
)(),(
.
Условия минимума записываются стандартным образом:
0),(
baQ
a
,
0),(
baQ
b
,
0),(
baQ
aa
,
0),(
baQ
bb
,
0
),(),(
),(),(
baQbaQ
baQbaQ
bbba
abaa
,
где производные первого и второго порядка имеют вид
n
i
ii
n
i
i
n
i
ia
yxxbxabaQ
111
2
),(
,
n
i
i
n
i
ib
ynbxabaQ
11
),(
,
n
i
iaa
xbaQ
1
2
),(
,
nbaQ
bb
),(
,
n
i
ibaab
xbaQbaQ
1
),(),(
.
Для упрощения записи нижеследующих формул введем сокращенные обозначения для
сумм, входящих в формулы для производных:
n
i
i
x
n
x
1
22
1
,
n
i
i
x
n
x
1
1
,
n
i
ii
yx
n
<xy>
1
1
,
n
i
i
y
n
y
1
1
<
0)(
1
1
1
222
2
2
n
i
ix
xx
n
xx
x
xx
S
.
Поскольку в рассматриваемом конкретном случае достаточные условия минимума выпол-
няются автоматически, оценка коэффициентов сводится к решению системы линейных
уравнений, определяемых необходимым условием экстремума
, 1
,
2
ybxa
xyxbxa
2
~
x
S
yxxy
a
,
2
2
~
x
S
xyxyx
b
.
Поскольку описанный метод нахождения коэффициентов линейной зависимости основан
на минимизации суммы квадратов отклонений расчетных значений от наблюдаемых, он
называется метод наименьших квадратов.
Подстановка в суммы, вместо измеренных значений
y
i
соответствующих им случайных
величин
iii
zbaxy
ˆ
ˆ
позволяет записать коэффициенты линейной зависимости как слу-
чайные величины, являющиеся линейными функциями случайных шумов
z
i
:
n
i
ii
x
zxx
nS
aa
1
2
ˆ
)(
1
ˆ
,
n
i
ii
x
zxxx
nS
bb
1
2
2
ˆ
)(
1
ˆ
.
Эти формулы являются основой для исследования статистических свойств коэффициентов
линейной зависимости.
Так как в рамках выдвинутых гипотез шумы являются независимыми случайными вели-
чинами, распределенными по закону
N( , )0
, законы распределения для случайных вели-
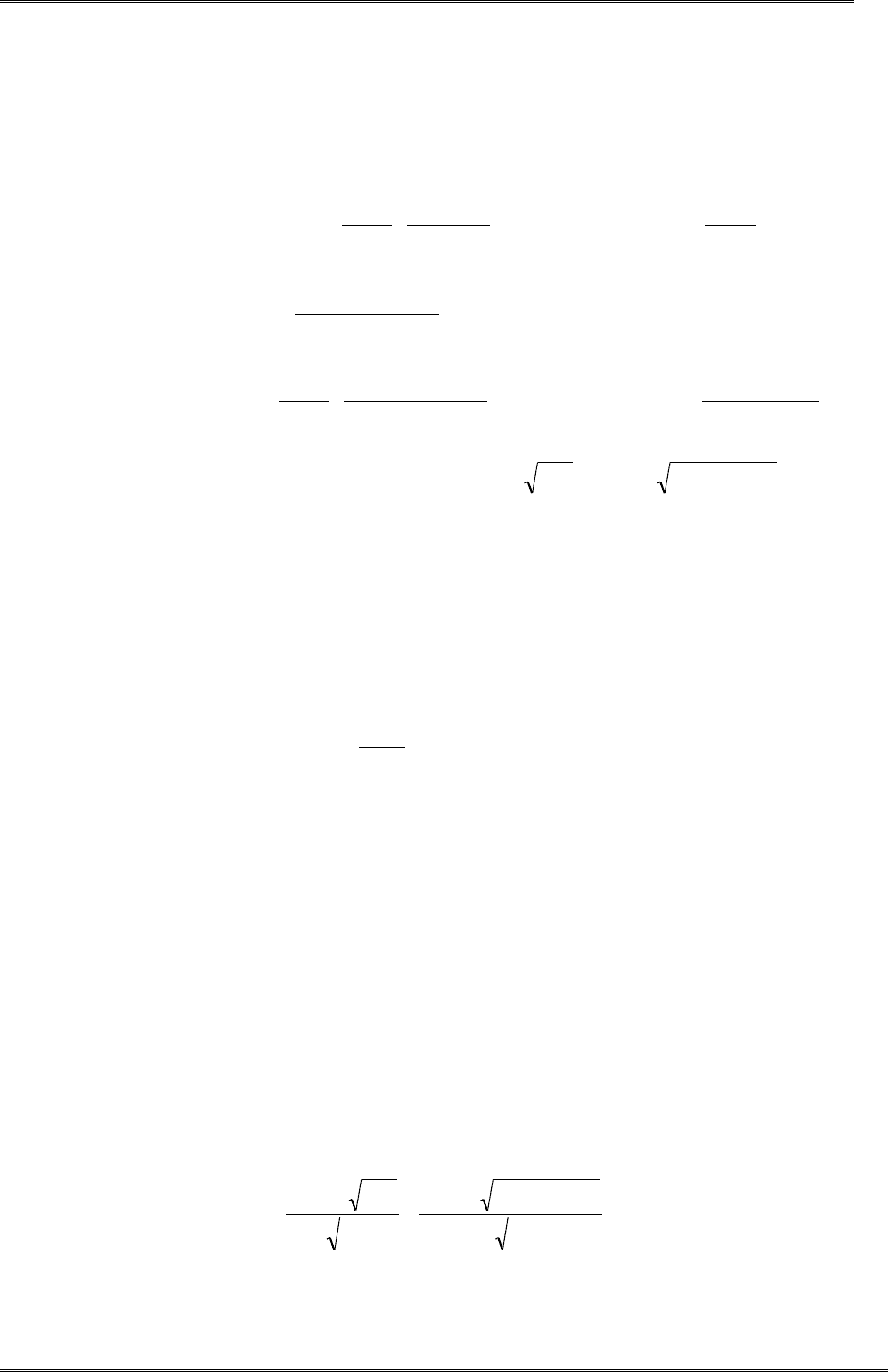
10
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
чин
a
ˆ
и
b
ˆ
можно получить при помощи преобразований характеристических функций
( ) exp( / )
z
2 2
2
при следующих линейных преобразованиях независимых случай-
ных величин:
awawwz
nS
xx
wz
N
i
ii
x
i
ii
ˆˆˆˆ
ˆ
ˆ
ˆ
1
2
,
nS
ia
nS
xx
x
i
x
i
2
22
2
2
22
22
2
exp)exp(
2
exp)2/exp(
,
bvbvvz
nS
xxx
vz
N
i
ii
x
i
ii
ˆ
ˆ
ˆˆ
ˆ
ˆ
ˆ
1
2
2
,
nS
x
ib
nS
xxx
x
i
x
i
2
222
2
2
222
22
2
exp)exp(
2
exp)2/exp(
.
Следовательно,
a
ˆ
и
b
ˆ
имеют распределения
)/,(
2
nSaN
x
)/,(
22
nSxbN
x
соответ-
ственно. Поскольку в теоретическом пределе
n
стандартные отклонения полученных
нормальных распределений стремятся к нулю, полученные по методу наименьших квад-
ратов оценки коэффициентов являются состоятельными точечными оценками.
Для получения интервальных оценок для коэффициентов линейной зависимости необхо-
димо, как и при получении оценки среднего значения на основе t- распределения, исполь-
зовать оценки стандартного отклонения помех на основе исходной выборки наблюдений.
Для этого рассматривается случайная величина называемая остаточной дисперсией
n
i
ii
bxay
n
Q
1
2
)
~
~
ˆ
(
2
1
ˆ
.
в которую входят оценки коэффициентов линейной зависимости, полученные методом
наименьших квадратов. Статистические свойства остаточной дисперсии являются следст-
вием следующего обобщения теоремы об ортогональном разложении:
Пусть случайные величины
niz
i
,3,2,1 ,
ˆ
статистически независимы и имеют одина-
ковое распределение
N( , )0
. Тогда справедливо разложение:
)/()
ˆ
(/)
ˆ
(/
ˆ
)2(/
ˆ
22222222
1
22
xSbbnSaanQnz
xx
n
i
i
,
где случайные величины
2
/
ˆ
)2(
Qn
и
222
/)
ˆ
(
x
Saan
,
)/()
ˆ
(
2222
xSbbn
x
независимы
и распределены по закону
-квадрат с
2n
степенями свободы и одной степенью сво-
боды соответственно.
Отсюда следует, что случайные величины
Q
nSaa
x
ˆ
)
ˆ
(
2
,
Q
xnSbb
x
ˆ
/)
ˆ
(
22
имеют
t
- распределения
2n
степенями свободы, а интервальные оценки для коэффици-
ентов линейной зависимости получаются из условия
ppttP
nn
))(|
ˆ
(|
22
и имеют вид:

11
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
nSQptaa
xn
2
2
/)(|
~
|
,
nSxQptbb
xn
22
2
/)(|
~
|
,
где
n
i
ii
bxay
n
Q
1
2
)
~
~
(
2
1
, - значение остаточной дисперсии, вычисленное по исход-
ной выборке и полученным оценкам коэффициентов
a
~
,
b
~
.
Если коэффициент наклона линейной зависимости
a
~
настолько мал, что его доверитель-
ный интервал накрывает нулевое значение, говорить о наличии статистически значимой
связи между переменными
yx,
не имеет смысла. Для подтверждения отсутствия стати-
стически значимой связи между исследуемыми переменными следует осуществить про-
верку нулевой гипотезы
0a
против альтернативы
0a
. Для этого используется так на-
зываемое распределение Фишера (см. приложение). В рассматриваемом случае, отноше-
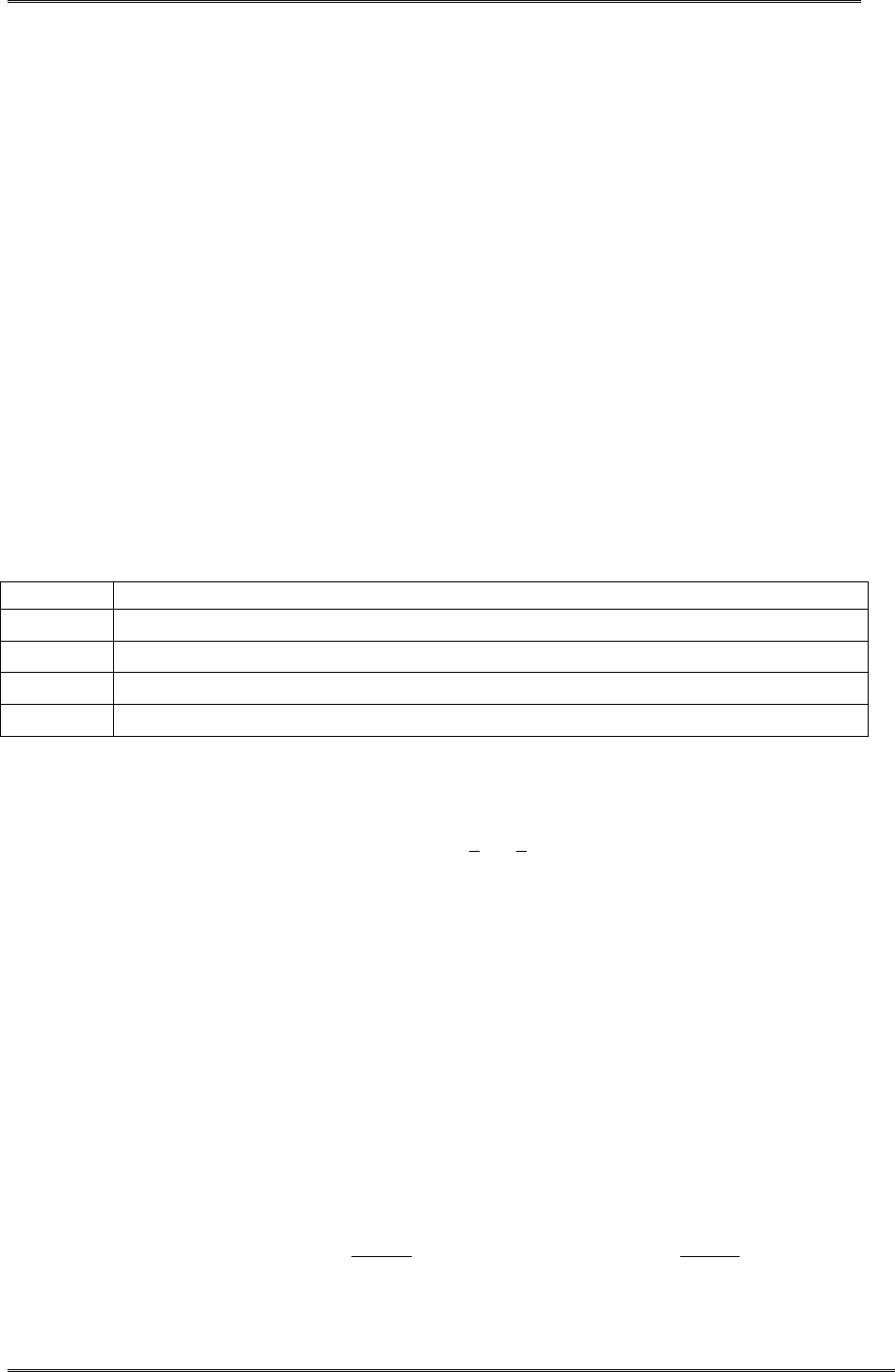
ние
Q
San
F
x
n
ˆ
ˆ
22
2,1
имеет распределение Фишера с
2,1 n
степенями свободы. Тогда уровнем значимости для
нулевой гипотезы
0a
против альтернативы
0a
будет вероятность события
)/
ˆ
(
22
2;1
QSnaFPSL
xn
,
и малые значения уровня значимости свидетельствуют против нулевой гипотезы, то есть в
пользу статистически значимой связи между переменными
yx,
.
Другой мерой адекватности модели данным наблюдения является коэффициент детерми-
нации
R
2
, определяемого формулой
n
k
k
n
k
k
n
k
k
yy
Qn
yy
ybxa
R
1
2
1
2
1
2
2
)(
)2(
1
)(
)
~
~
(
.
Коэффициент детерминации характеризует отношение разбросов расчетных и наблюдае-
мых значений
y
относительно выборочного среднего
y
. Чем ближе значения коэф-
фициента детерминации к единице, тем лучше полученная линейная зависимость описы-
вает данные наблюдений.
Для окончательной проверки адекватности построенной модели линейной зависимости
исходным данным, необходимо проверить справедливость гипотез, лежащих в основе мо-
дели. Для этого проводят анализ остатков, то есть после вычисления оценок коэффици-
ентов
a
~
,
b
~
, получают выборку остатков
nibxayz
iii
,2,1,
~
~
и для этой выборки
проверяют гипотезы «остатки независимы» и «остатки имеют распределение
),0(
N
».
Последнюю гипотезу можно проверить по критерию Пирсона, предварительно сделав
оценку стандартного отклонения с помощью статистики «выборочная дисперсия». Одна-
ко, эта проверка будет иметь смысл лишь тогда, когда остатки независимы и имеют оди-
наковую дисперсию.
Проверка гипотезы о независимости остатков может быть проведена при помощи так на-
зываемой статистики Дарбина - Уотсона

12
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
n
i
i
n
i
iiii
n
i
i
n
i
ii
z
zzzz
z
zz
DW
1
2
1
1
2
1
2
1
1
2
1
1
2
1
)2()(
.
значения которой лежат в интервале
]4,0[
. Качественное поведение статистики Дарбина –
Уотсона можно понять из следующих соображений. Когда остатки в соседних точках на-
блюдения сильно зависят друг от друга, значения статистики близко к границам интервала
(
0DW
при
ii
zz
1
, и
4DW
при
ii
zz
1
), а когда остатки в соседних точках незави-
симы
0
1
1
1
n
i
ii
zz
, то
2DW
близко к середине интервала.
Проверка гипотезы об одинаковой дисперсии остатков (так называемый тест на гомоске-
дастичность) проводится при помощи статистики Голдфельда – Квандта
n
ni
i
n
i
i
n
ni
i
n
i
i
zz
zz
GQ
3/2
2
3/
1
2
3/2
2
3/
1
2
,min
,max
,
которая сравнивает суммы квадратов остатков первой и последней трети выборки остат-
ков. Значения статистики близкие к единице свидетельствуют в пользу гипотезы об оди-
наковой дисперсии остатков, а сильные отклонения статистики от единицы, - против этой
гипотезы.
Замечания об обобщении простейшей линейной модели
Рассмотренная выше простейшая модель линейной зависимости между двумя перемен-
ными может быть обобщена двумя путями.
Во-первых, для парных наблюдений
);( xy
можно рассмотреть нелинейные зависимости
между переменными
)()()(
22110
xfaxfaxfaay
mm
.
Во вторых, для множественных наблюдений
);;;(
21 m
zzzy
можно рассматривать линей-
ные зависимости одной величины от нескольких переменных
);;(
21 m
zzz
mm
zazazaay
22110
.
При этом в обоих случаях значения коэффициентов модели
);;;(
210 m
aaaa
находятся пу-
тем минимизации квадратичного отклонения расчетных значений от наблюдаемых, то
есть по методу наименьших квадратов.
Оба описанных обобщения простейшей модели отличаются от нее главным образом
большими вычислительными сложностями. В то же время для проверки гипотез, лежащих
в основе модели, по-прежнему использовать критерий Фишера, коэффициент детермина-
ции и анализ остатков. Поскольку реальная обработка данных в рамках многомерных и
нелинейных моделей возможна лишь с применением компьютера, полная ясность в работе
с простейшей линейной моделью настоятельно необходима для уверенной интерпретации
результатов компьютерной обработки данных.
13
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Критерии проверки гипотез, основанные на интервальных оценках
В настоящем разделе будут приведены дополнительные примеры проверки статистиче-
ских гипотез для нормально распределенных выборок. Приводимые примеры выбирались
так, чтобы показать основные идеи, лежащие в основе проверки гипотез, не затеняя суть
сложными вычислительными подробностями.
Проверка гипотез будет осуществляться по следующей общей схеме:
Формулируются основная (нулевая) и альтернативная гипотезы
На основе данных и формулировок гипотез вычисляется уровень значимости
По вычисленному значению уровня значимости принимается решение в пользу ос-
новной или альтернативной гипотезы.
Наиболее сложным в приведенной схеме является понятие уровня значимости
SL
(signi-
ficance level).
Уровень значимости связан со степенью недоверия к основной гипотезе формулой:
Степень недоверия основной гипотезе = 1 - уровень значимости основной гипотезы.
Чем ниже значения уровня значимости, тем больше недоверие к основной гипотезе. Как
будет видно из приведенных ниже примеров, уровень значимости зависит не только от
формулировки основной гипотезы, но и от формулировки альтернативной гипотезы. Тра-
диционная интерпретация уровней значимости приведена в следующей таблице.
SL
Стандартная интерпретация
1,0SL
Данные согласуются с основной гипотезой
05,0SL
Возможна значимость. Есть сомнения в справедливости основной гипотезы
02,0SL
Значимость. Сильные доводы против основной гипотезы
01,0SL
Высокая значимость. Основная гипотеза почти наверняка ложная
Проверка равенства двух средних значений при известном стандартном отклонении
Для двух выборок статистически независимых случайных величин, объемов
1
n
и
2
n
соот-
ветственно найдены оценки средних значений
x
1
и
x
2
. Требуется определить, является ли
статистически значимой разность между полученными значениями, если известно, что
выборки распределены по нормальному закону с равными стандартными отклонениями.
Формулируем основную и альтернативную гипотезы.
Основная гипотеза: разность средних значений равна нулю.
Альтернативная гипотеза: разность средних значений не равна нулю.
Характеристические функции случайных величин «выборочное среднее» для рассматри-
ваемых выборок имеют вид
)2/exp()exp()( );2/exp()exp()(
2
22
221
22
11
niania
.
Если верна основная гипотеза, имеет место равенство истинных средних значений
a a
1 2
и характеристическая функция разности выборочных средних имеет вид
21
21
2222
21
21
22
21
2
~
);2/
~
exp()
2
exp()(
nn
nn
nn
nn
,
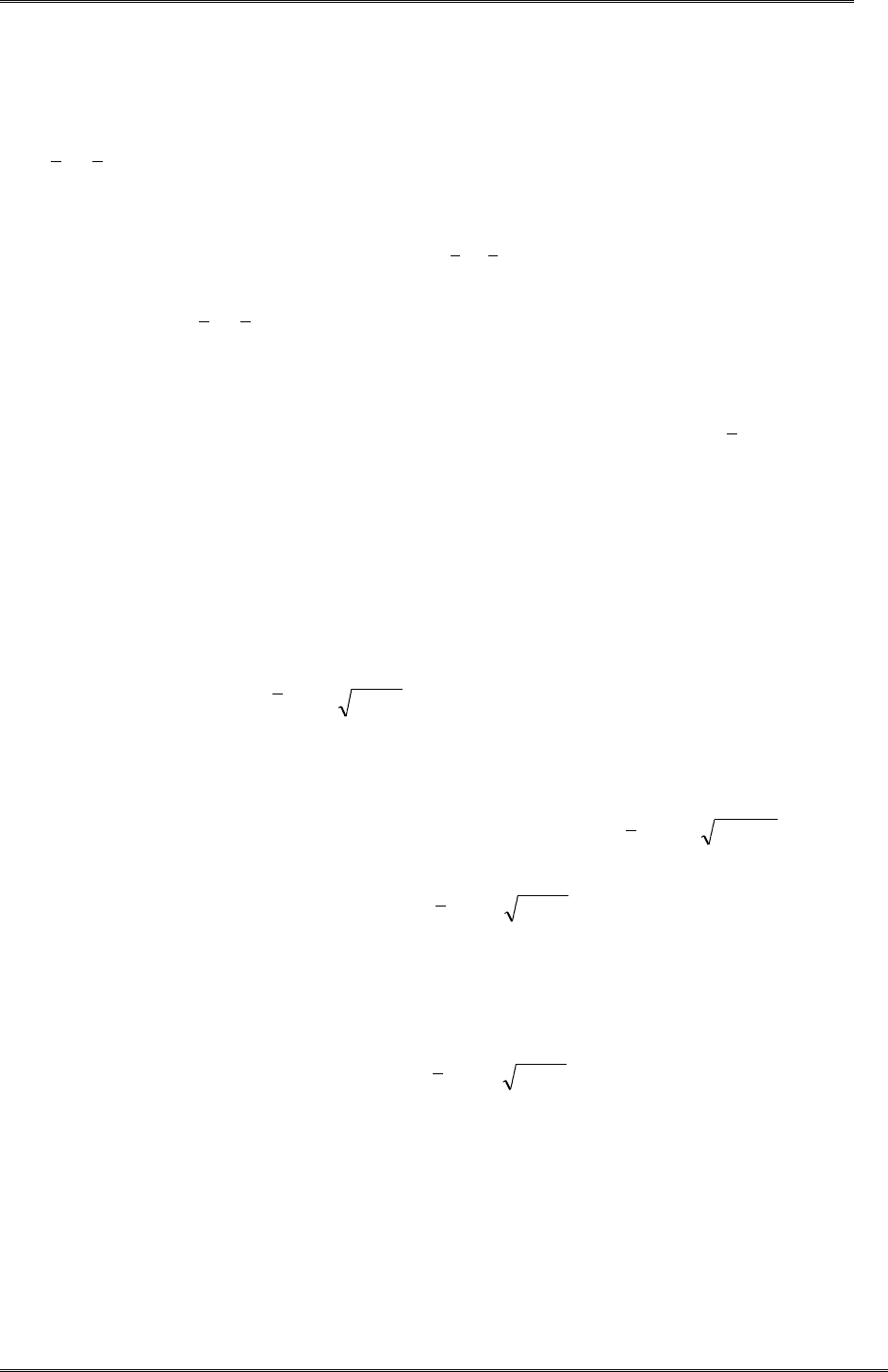
14
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
является характеристической функцией нормального распределения
N( ,
~
)0
, а нормиро-
ванная случайная величина
(
) /
~
u x x
1 2
будет распределена по закону
N( , )0 1
.
Уровень значимости основной гипотезы относительно выбранной альтернативной гипоте-
зы определяется из следующих соображений. Если верна основная гипотеза, то в пользу
справедливости основной гипотезы будут говорить малые значения наблюдаемой разно-
сти
| |x x
1 2
, а большие наблюдаемые значения этой разности будут свидетельствовать
против основной гипотезы. Поэтому, для вычисления уровня значимости основной гипо-
тезы против выбранной альтернативы естественно использовать формулу
)
~
/|||
ˆ
(|
21
xxuPSL
,
определяющую вероятность наблюдения в других экспериментах значений разности вы-
борочных средних
|
|x x
1 2
, превосходящих вычисленную по рассматриваемым выборкам.
Проверка равенства среднего значения выборки заданному значению при неизвестном
стандартном отклонении
Для нормально распределенной выборки вычислены выборочное среднее
x
и выборочная
дисперсия.
S
2
. На основании дополнительных соображений предполагается, что среднее
значение распределения равно числу
A
. Требуется проверить, равно истинное среднее
предполагаемому гипотетическому значению или превосходит его.
Формулируем основную и альтернативную гипотезы.
Основная гипотеза:
a A
.
Альтернативная гипотеза:
a A
.
По теореме об ортогональном разложении для нормально распределенной выборки из-
вестно, что отношение
nSaxt /
ˆ
/)
ˆ
(
ˆ
2
имеет
t
-распределение с
1n
степенью свобо-
ды, а согласно основной гипотезе
a A
.
Уровень значимости основной гипотезы относительно выбранной альтернативы опреде-
ляем из следующих соображений. Поскольку в пользу альтернативной гипотезы свиде-
тельствуют наблюдения больших положительных отклонений
( ) / /x A S N
2
, уровень
значимости будет вычисляться по формуле
nSAxtPSL
n
//)(
ˆ
2
1
.
Если при сохранении основной гипотезы заменить альтернативную гипотезу условием
a A
, в пользу альтернативной гипотезы будут говорить как положительные, так и отри-
цательные отклонения выборочного среднего от гипотетического значения. В этом случае
и уровень значимости будет вычисляться по формуле
nSAxtPSL
n
//||
ˆ
2
1
.
Проверка гипотезы о равенстве стандартного отклонения выборки заданному значению
Пусть по исходной нормально распределенной выборке вычислена выборочная дисперсия
S
2
. Требуется проверить, что истинное стандартное отклонение равно некоторому значе-
нию
0
, определенному из дополнительных соображений.
Формулируем основную и альтернативную гипотезы.
Основная гипотеза:
0
.
Альтернативная гипотеза:
0
.

15
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Так как случайная величина
22
/
ˆ
)1(
Sn
распределена по закону
-квадрат с
1n
сте-
пенью свободы, а в пользу альтернативной гипотезы свидетельствуют наблюдения значе-
ний
/S
2
0
2
существенно превосходящих единицу, уровень значимости будет вычисляться
по формуле
2
0
22
1
/)1(
ˆ
SNPSL
N
.
Если заменить исходную альтернативную гипотезу условием
0
, то в пользу этой
альтернативной гипотезы будут указывать значения
S
2
0
2
/
как много большие, так и
много меньшие единицы. Поэтому формула для определения уровня значимости должна
быть изменена следующим образом:
22
0
2
1
2
0
22
1
/)1(
ˆ
/)1(
ˆ
SnPSnPSL
nn
.
Проверка гипотезы о равенстве дисперсий двух независимых выборок
Пусть по двум выборкам объема
1
n
и
2
n
измерений одной и той же случайной величины,
определены выборочные дисперсии
S S
1
2
2
2
,
. Требуется установить, является ли статистиче-
ски значимым различие между полученными значениями выборочных дисперсий.
Формулируем основную и альтернативную гипотезы.
Основная гипотеза:
S S
1
2
2
2
.
Альтернативная гипотеза:
S S
1
2
2
2
.
Для проверки гипотез, основанных на сравнении дисперсий нормально распределенных
выборок, используется распределение Фишера (см. приложение). Так как случайные ве-
личины
22
11
/
ˆ
)1(
Sn
и
22
22
/
ˆ
)1(
Sn
имеют распределения
-квадрат с
1
1
n
и
1
2
n
степенями свободы, случайная величина
2
2
2
1
ˆ
/ SS
имеет распределение Фишера с
1
1
n
,
1
2
n
степенями свободы, а случайная величина
/
S S
2
2
1
2
- распределение Фишера с
1
2
n
,
1
1
n
степенями свободы. Поскольку в пользу альтернативной гипотезы свидетельствуют
значительные отклонения наблюдаемого значения отношения выборочных дисперсий от
единицы, уровень значимости вычисляется по формулам:
2
1
2
21,1
2
2
2
11,1
/
ˆ
/
ˆ
1221
SSFPSSFPSL
nnnn
для
2
2
2
1
SS
,
2
1
2
21,1
2
2
2
11,1
/
ˆ
/
ˆ
1221
SSFPSSFPSL
nnnn
для
2
2
2
1
SS
.
Элементы непараметрических методов статистики
Рассмотренные выше методы анализа данных существенным образом опирались на гипо-
тезу о нормальном распределении случайных шумов искажающих данные измерений или
наблюдений. Хотя гипотезу о нормальном распределении шумов можно заменить гипоте-
зой о некотором другом законе распределения, она все равно будет наиболее слабым зве-
ном, так как гипотезу о законе распределения наиболее трудно проверить, особенно когда
требуется установить статистическую независимость шумов в различных точках наблю-
дения. Рассматриваемые ниже методы анализа данных свободны от гипотез относительно
закона распределения данных измерений (или наблюдений).
Критерии, основанные на эмпирической функции распределения
Одним из способов наглядного представления данных является так называемая эмпириче-
ская функция распределения. Процедура построения эмпирической функции распределе-
16
Начальные сведения по математической статистике
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
ния опирается на представление исходной выборки в виде упорядоченного по возраста-
нию множества, которое называется вариационным рядом.
Эмпирическая функция распределения строится по следующему определению
По исходной выборке строится ее вариационный ряд.
)(}),,,(
)()3()2()1(321 nn
xxxxxxxx
Значения эмпирической функции распределения вычисляются по формуле
nxnnxF
xx
n
k
/)(/1)(
,
где
n x( )
- число элементов выборки удовлетворяющих условию
x x
k
.
Из этого определения следует, что эмпирическая функция распределения обращается в
нуль при
x x
( )1
, равна единице при
x x
N
( )
, и изменяется скачком на значениях аргу-
мента, равных элементам вариационного ряда.
Критерий Колмогорова используется для проверки гипотезы о соответствии распределе-
ния данных исходной выборки некоторому теоретическому закону распределения. Крите-
рий основан на измерении «расстояния» между эмпирической функцией распределения
исходной выборки и теоретической функцией распределения тестируемого теоретическо-
го закона распределения.
В критерии Колмогорова проверяется нулевая гипотеза: «выборка получена из распреде-
ления, описываемого функцией распределения
F x( )
» против альтернативы: «выборка по-
лучена из распределения, не описываемого функцией распределения
F x( )
».
В качестве статистики критерия выступает максимальное отклонение эмпирической
функции распределения выборки
)(xF
n
от теоретической функции распределения
F x( )
,
соответствующей проверяемому закону распределения:
|)()(|max xFxFD
n
x
n
.
Уровень значимости для основной гипотезы равен вероятности получения в других экспе-
риментах значений статистики критерия больше наблюдаемого
2
)
ˆ
(
nn
DDPSL
.
При объемах выборки
40n
, гипотезу о соответствии эмпирической функции распреде-
ления тестируемому теоретическому закону можно проверять путем сравнения получен-
ной по выборке статистики критерия Колмогорова с критическим значением, вычислен-
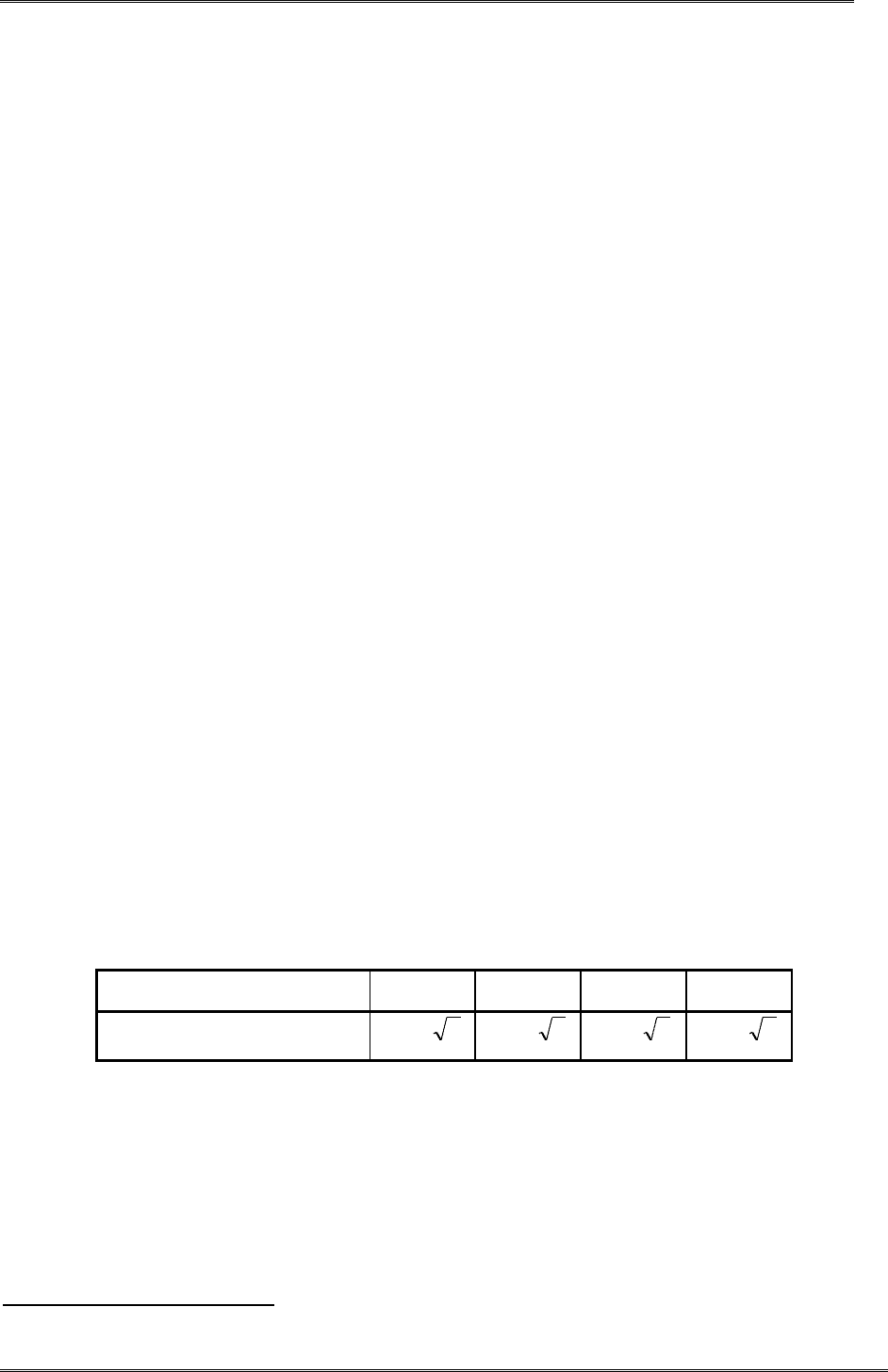
ным по следующей таблице.
Уровень значимости
SL
0,20
0,10
0,05
0,01
Критическое значение
c
D
n/07,1
n/22,1
n/36,1
n/66,1
Нулевая гипотеза принимается, если наблюдаемое значение статистики критерия не пре-
восходит критическое значение.
Критерий Смирнова используется для сравнения двух выборок. Предполагается, что для
каждой выборки предварительно построены эмпирические функции распределения
)(
1
xF
n
и
)(
2
xG
n
.
2
Такие вероятности приведены в таблицах Большев Л. Н., Смирнов Н. В. Таблицы математической стати-
стики. - М.: Наука, 1983. - 414 с.
