Алексеев Д.В. Конспекты по общему курсу математики
Подождите немного. Документ загружается.


Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
16
специальные функции (в практической работе с последним случаем приходится встре-
чаться сплошь и рядом!).
Обобщение понятия определенного интеграла
Определенный интеграл от функций с конечными разрывами
Простейшим обобщением понятия определенного интеграла от непрерывной функции яв-
ляется определенный интеграл от функции с конечными разрывами (разрывами первого
рода). В основу такого обобщения достаточно положить свойство аддитивности. Напри-
мер, если подынтегральная функция имеет внутри интервала интегрирования единствен-
ную точку разрыва первого рода
c
, то в силу непрерывности подынтегральной функции
на интервалах
),( ca
и
),( bc
b
c
c
a
b
a
dxxfdxxfdxxf )()()(
.
Более строгое обоснование данного результата состоит в «вырезании» точки разрыва
0,)()()()()(
с
с
с
с
b
с
с
a
dxxfdxxfdxxfdxxfI
,
и рассмотрении предела
)(lim
0
I
с помощью формулы
)())()(()()(
ocfcfdxxfdxxf
с
с
с
с
.
Обобщение описанного результата на случай, когда на интервале интегрирования присут-
ствует любое конечное число точек разрыва первого рода тривиально.
Определенный интеграл от функций с бесконечными разрывами
(несобственный интеграл первого рода)
Определенный интеграл от функции с бесконечными разрывами определяется при помо-
щи процедуры предельного перехода в определенном интеграле. Рассмотрим простейший
вариант, когда единственная точка разрыва подынтегральной функции попадает на одну
из границ интервала интегрирования, например, на нижнюю границу. В этом случае ис-
ходный интеграл «обрезают» на нижней границе, превращая его в определенный интеграл
от непрерывной функции, и рассматривают поведение функции
0,)()(
b
a
dxxfI
Когда эта функция имеет конечный предел
)(lim
0
I
, говорят что интеграл от функции с
бесконечным разрывом, называемый несобственным интегралом первого рода, сходится
(существует). В противном случае говорят, что несобственный интеграл расходится (не
существует).
Если точка разрыва попадает внутрь интервала интегрирования, несобственный интеграл
первого рода определяется при помощи «вырезания» точки разрыва через пару несобст-
венных интегралов, с точками разрыва на границе интервала
0,0,)()()()(
212211
2
1
b
с
с
a
dxxfdxxfII
.

Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
17
Такой несобственный интеграл считается сходящимся, если сходятся оба несобственных
интеграла в правой части равенства.
Существуют специфический случай несобственных интегралов с точной разрыва внутри
интервала интегрирования, когда интеграл расходится в определенном выше смысле, но
сходится при «симметричном вырезании» точки разрыва
0,)()()(
b
с
с
a
dxxfdxxfI
, (предел
)(lim
0
I
конечный).
В этом случае говорят, что несобственный интеграл сходится в смысле главного значения
по Коши, и обозначается символом
b
a
dxxf )(Vp
.
Определенный интеграл от непрерывной функции по бесконечному
интервалу (несобственный интеграл второго рода)
Простейшими несобственными интегралами второго рода являются интегралы от непре-
рывных функций вида
a
dxxf )(
,
b
dxxf )(
.
Для определения данных интегралов, их сводят к обычным определенным интегралам,
путем «обрезания» на бесконечной границе интегрирования, например,
R
a
dxxfRI )()(
.
Если предел
)(lim RI
R
конечное число, то говорят, что несобственный интеграл второго
рода сходится. В противном случае говорят, что интеграл расходится.
Несобственный интеграл от непрерывной функции по всей действительной оси определя-
ется при помощи свойства аддитивности через два несобственных интеграла, рассмотрен-
ных выше
1
1
2
2
)(lim)(lim)(
R
a
R
a
R
R
dxxfdxxfdxxf
.
Интеграл считается сходящимся, когда сходятся оба интеграла в правой части равенства.
Если по такому определению интеграл расходится, но к конечному пределу сходится оп-
ределенный интеграл по симметричному интервалу, то говорят, что несобственный инте-
грал второго рода сходится в смысле главного значения по Коши.
R
R
R
dxxfdxxf )(lim)(Vp
.
Замечание. Если исходный интеграл является несобственным по нескольким причинам,
его в точках непрерывности подынтегральной функции разбивают на несколько слагае-
мых, каждое из которых является простейшим несобственным интегралом («несобствен-
ным интегралом по единственной причине»). Такой несобственный интеграл считается
сходящимся только тогда, когда сходятся все определяющие его слагаемые.

Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
18
Техника вычисления определенных и
несобственных интегралов
Замена переменной в определенных и несобственных интегралах
При вычислении неопределенных интегралов используются разнообразные замены пере-
менных, определяемые дифференцируемыми функциями. Для вычисления определенных
интегралов это прием также применим. Он формулируется следующим образом:
Пусть непрерывно дифференцируемая функция
)(tu
задает взаимно однозначное ото-
бражение интервала
],[
на интервал интегрирования
],[ ba
функции
)(xf
. Тогда
buaudttutufdxxf
b
a
)(,)(,)())(()(
.
Требование непрерывности производной
)(tu
обеспечивает непрерывность функции
)())(( tutuf
, а взаимно однозначность отображения интервалов, строгая монотонность
)(tu
, гарантирует единственность решений уравнений
buau )(,)(
.
При вычислениях несобственных интегралов с помощью замены переменной, необходимо
соблюдать те же ограничения, что и при вычислении определенных интегралов. Такие
вычисления могут проводиться как для исследования сходимости рассматриваемого инте-
грала, так и для вычисления сходящегося интеграла. Основной результат, касающийся за-
мены переменной в сходящемся несобственном интеграле состоит в следующем:
сходящийся несобственный интеграл заменой переменной может быть преобразован в
обычный определенный интеграл.
Когда подынтегральная функция обладает определенной симметрией, для сокращения
вычислений, определенный интеграл может быть упрощен на основе симметрии подынте-
гральной функции. Например, любой интеграл от нечетной функции по симметричному
интервалу обращается в нуль, а интеграл от четной функции по симметричному интервалу
равен удвоенному интегралу по половине этого интервала. Если интегрируется периоди-
ческая функция по промежутку в который укладывается целое число периодов, интеграл
может быть записан как произведение интеграла по одному периоду на число периодов в
рассматриваемом интервале.
Исследование сходимости несобственных интегралов
Исследование сходимости несобственных интегралов часто удобно проводить, записывая
приближенную формулу для подынтегральной функции в окрестности разрыва (для не-
собственных интегралов первого рода) или при больших значениях переменной (для не-
собственных интегралов второго рода). Соответствующие результаты, называются при-
знаками сходимости несобственных интегралов и доказываются прямым вычислением.
Признак сходимости несобственного интеграла первого рода.
Несобственный интеграл
a
a
dxxf )(
сходится, если при
ax
подынтегральная функция
имеет постоянный знак и является бесконечно большой функцией порядка
1
,
)(1)()( axOaxCxf
.
Признак сходимости несобственного интеграла второго рода.
Несобственный интеграл
R
dxxf )(
сходится, если при
x
подынтегральная функция

Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
19
имеет постоянный знак и является бесконечно малой функцией порядка
1
,
)(1)(
1
xOCxxf
x
.
Признак сходимости несобственных интегралов второго рода, для подынтегральных
функций, имеющих колебательный характер.
Несобственный интеграл
R
dxxxg )sin()(
сходится, если функция
)(xg
имеет постоянный
знак и является бесконечно малой функцией порядка
0
,
)(1)(
1
xOCxxg
x
.
Для доказательства сходимости преобразуем интеграл при помощи формулы интегриро-
вания произведения
dxxO
x
x
CxO
x
x
CdxxO
x
x
C
R
R
R
)(1
)cos(
|)(1
)cos(
)(1
)sin(
1
1
11
.
Оба слагаемых в правой части равенства конечные числа, так как первое слагаемое равно
)(1
)cos(
1
RO
R
R
C
, а интеграл сходится в силу неравенства
RRR
dxxO
x
dxxO
x
x
dxxO
x
x
)(1
1
)(1
|)cos(|
)(1
)cos(
1
1
1
1
1
1
.
Приближенные оценки определенных интегралов
Когда первообразную вычислить аналитически невозможно, или весьма затруднительно,
для вычислений определенных интегралов прибегают к приближенным оценкам. Такие
оценки опираются либо на приближенные формулы для подынтегральной функции, либо
на смысл определенного интеграла как «площади под графиком». В последнем случае ис-
пользуемые для оценок формулы называются формулами численного интегрирования. Ес-
ли рассматриваемый интеграл является сходящимся несобственным интегралом, то для
численного интегрирования его следует свести к обычному определенному интегралу
подходящей заменой переменной.
Главная идея построения формул численного интегрирования состоит в разбиении интер-
вала интегрирования на «элементарные интервалы» малой длины. Затем на каждом эле-
ментарном интервале точный график подынтегральной функции приближают графиком
многочлена заданного порядка. Простейшим вариантом формулы численного интегриро-
вания является формула прямоугольников, оперирующая с многочленами нулевого поряд-
ка
N
ab
kafNIdxxf
N
k
b
a
,)()()(
1
0
.
Контроль точности вычислений, основанных на подобных формулах, осуществляется пу-
тем исследованиям сходимости получаемых результатов при увеличении числа интерва-
лов
N
.
8
8
Обычно число интервалов увеличивают вдвое и вычисления прекращают, когда при сравнении двух значе-
ний интеграла относительная
|)2(|/|)2()(| NININI
, или абсолютная
|)2()(| NINI
ошибка ста-
новится меньше заданной величины.
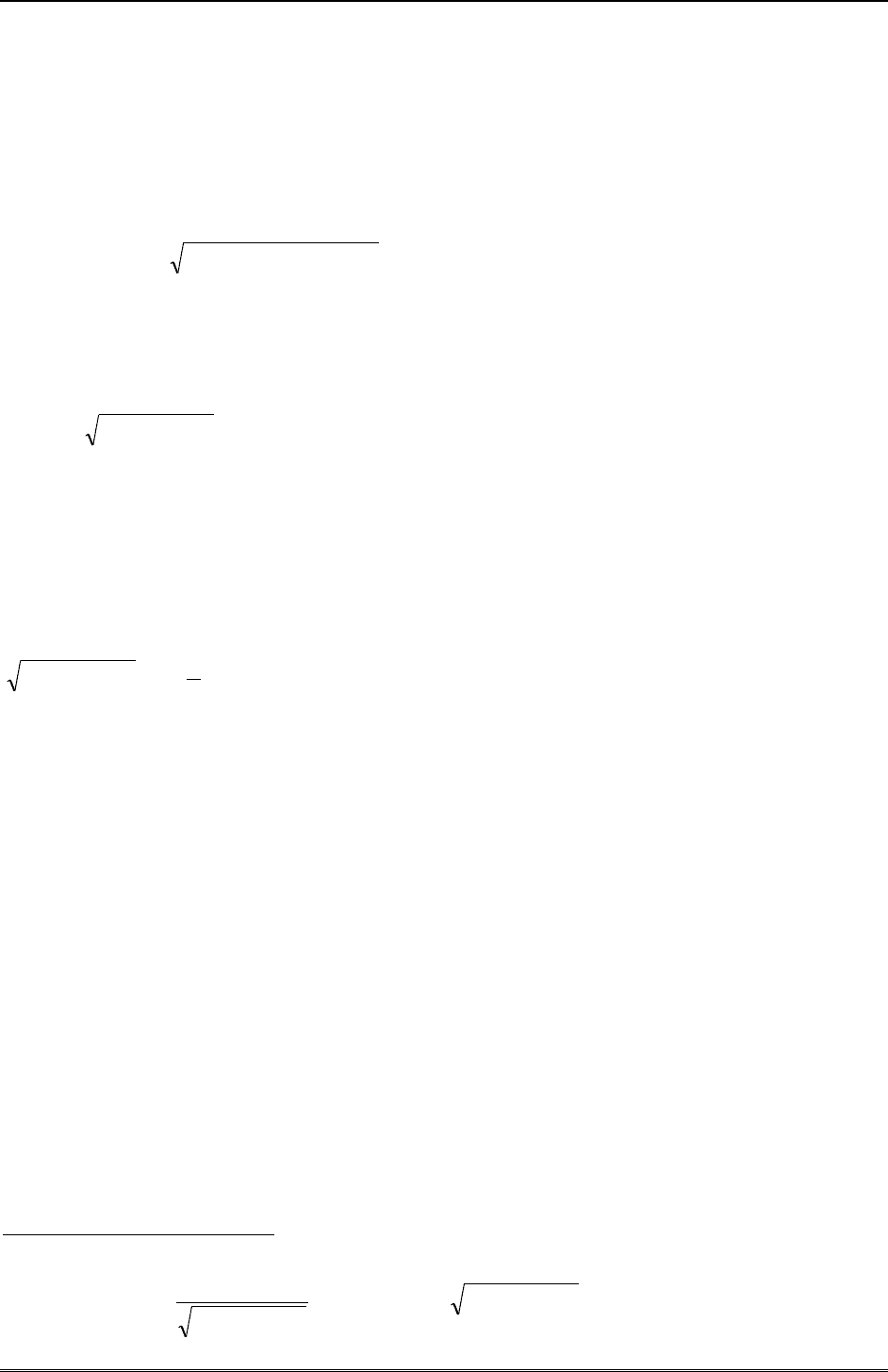
Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
20
Другой метод оценки определенных и несобственных интегралов основан на приближен-
ных формулах для подынтегральной функции, получаемых обычно при помощи подходя-
щих разложений подынтегральной функции или ее составляющей по формуле Тейлора.
В качестве примера оценки определенного интеграла получим приближенную формулу
для длины эллипса при малой разнице длин его полуосей. Эллипс задается векторной
функцией
))sin();cos(()( tbtatr
,
20 t
, а его длина выражается через интеграл от
длины вектора скорости
))cos();sin(()( tbtatv
.
2
0
2222
2
0
)(cos)(sin|)(| dttbtadttvL
.
Несмотря на кажущуюся простоту, первообразную подынтегральной функции выразить
через элементарные функции невозможно. Полагая, для определенности, что эллипс вы-
тянут вдоль оси ординат, запишем его длину в виде
222
2/
0
22
/1,)(sin14 bakdttkbL
.
Последняя формула выражает длину эллипса через специальную функцию, называемую
полным эллиптическим интегралом второго рода
9
. При конкретных значениях длин по-
луосей эллипса, необходимое значение полного эллиптического интеграла можно взять из
соответствующих справочников. В случае малой разницы между длинами полуосей
1k
, и длину эллипса можно оценить, разлагая квадратный корень по формуле Маклорена с
требуемой точностью, например,
)()(sin
2
1
1)(sin1
42222
kOtktk
,
)(4/12
42
kOkbL
.
В качестве примера оценки несобственного интеграла, получим приближенную формулу
для факториала при больших значениях переменной. Записав факториал через гамма-
функцию (см. следующий раздел):
00
))ln(exp(! dttntdtetn
tn
,
и сделав замену переменной
znt
, представим факториал в виде
0
`1
00
))ln((exp())ln(exp())ln(exp(! dzzznnndznznnzdtnznnzn
n
.
Из последней формулы видно, что в силу быстрого убывания показательной функции, при
больших значениях
n
и положительности функции
)ln()( zzz
, главный вклад в инте-
грал вносит окрестность точки
1z
, в которой функция
)(z
имеет локальный минимум.
Тогда интеграл можно оценить, используя квадратичное разложение
)(z
вблизи мини-
мума по формуле Тейлора
9
Специальные функции, называемые эллиптическими интегралами первого и второго рода задаются фор-
мулами
x
dt
tk
kxF
0
22
)(sin1
1
)|(
,
x
dttkkxE
0
22
)(sin1)|(
,
10 k
. При значениях пере-
менной
2/
x
эллиптические интегралы называются полными.
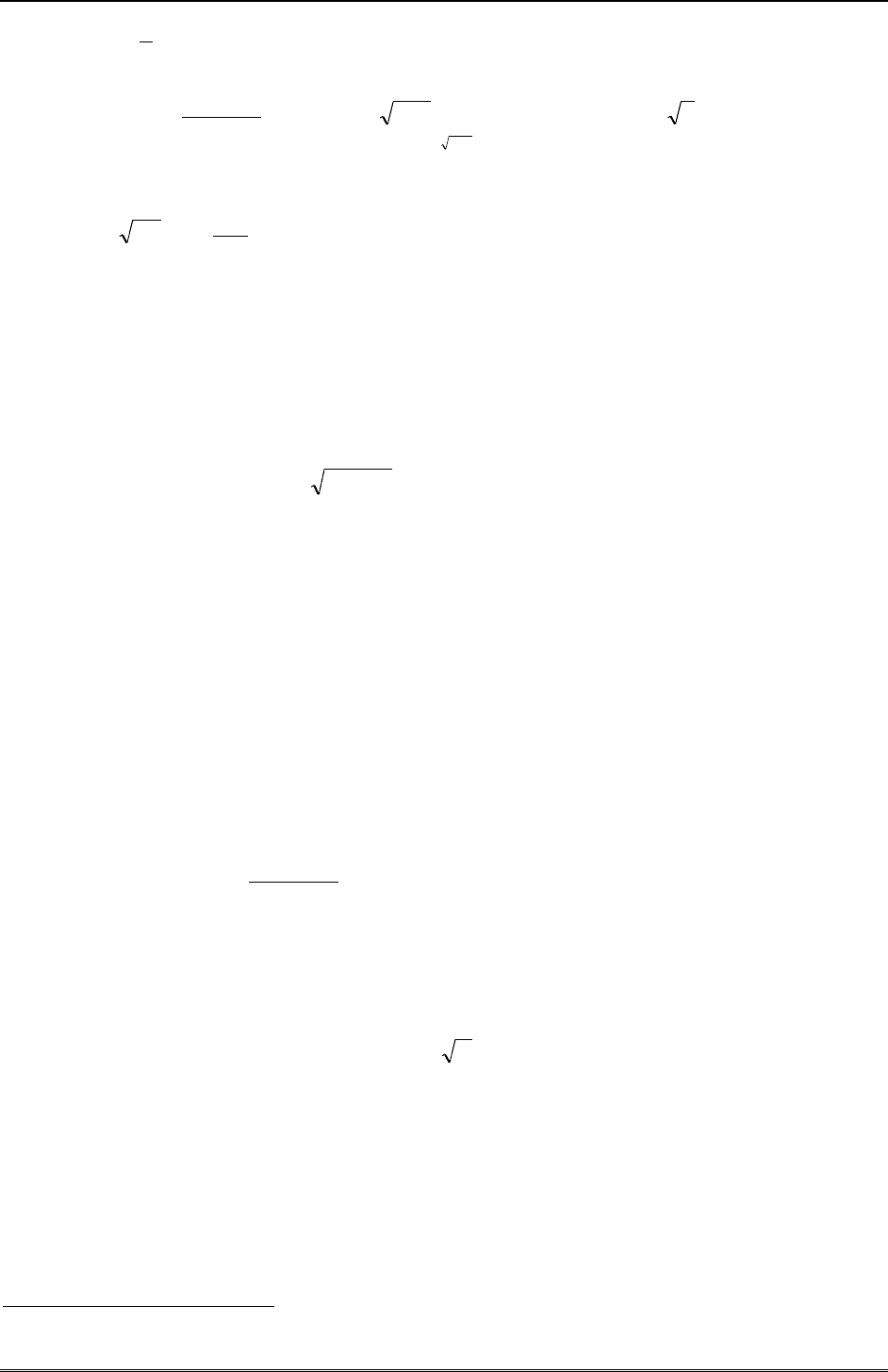
Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
21
2
1
)1(
2
1
1)ln(
zzz
z
duuenduunendz
zn
enn
nn
n
nnnn
)exp(2)exp(/2
2
)1(
exp!
22/1
2/
21
0
2
1
.
Полученная оценка дает главное приближение так называемой формулы Стирлинга
)(
12
1
12!
32/1
nO
n
enn
nn
.
Отсюда видно, что уже для значений переменной
10n
, главное приближение дает отно-
сительную погрешность вычислений менее одного процента.
Вычисление интегралов по их смысловому значению
Иногда вычисление определенного или несобственного интеграла может быть сделано во-
все без вычислений, непосредственно по его смысловому значению.
Рассмотрим простой пример:
a
a
dxxa
22
.
Хотя первообразную подынтегральной функции нетрудно найти аналитически, например,
при помощи замены
)sin(tax
, проще сразу записать ответ, опираясь на смысл этого
интеграла. Он выражает площадь полукруга
222
ayx
,
0y
, то есть равен
2/
2
a
.
В других случаях при подобных «вычислениях» опираются на знание некоторых часто
встречающихся функций. Например, полезно знать некоторые свойства функций Эйлера, -
гамма-функции
10
0,)exp()(
0
1
zdtttz
z
,
и бета-функции
0,,
)(
)`()(
)1(),(
1
0
11
ba
ba
ba
dtttbaB
ba
.
Основное свойство гамма-функции
)()1( zzz
,
легко доказывается при помощи формулы интегрирования произведения, а два частных
значения гамма-функции,
1)1(
и
)2/1(
, следует запомнить.
Замена переменной
)(sin
2
zt
дает представление бета-функции, которое очень удобно
при вычислении интегралов от произведений основных тригонометрических функций:
2/
0
1212
)(cos)(sin2),(
dzzzbaB
ba
.
Замена
)1/( uut
дает другое полезное представление бета-функции
10
Гамма-функцию иногда называют факториальной функцией, так она связана с факториалом
!)1( nn
.
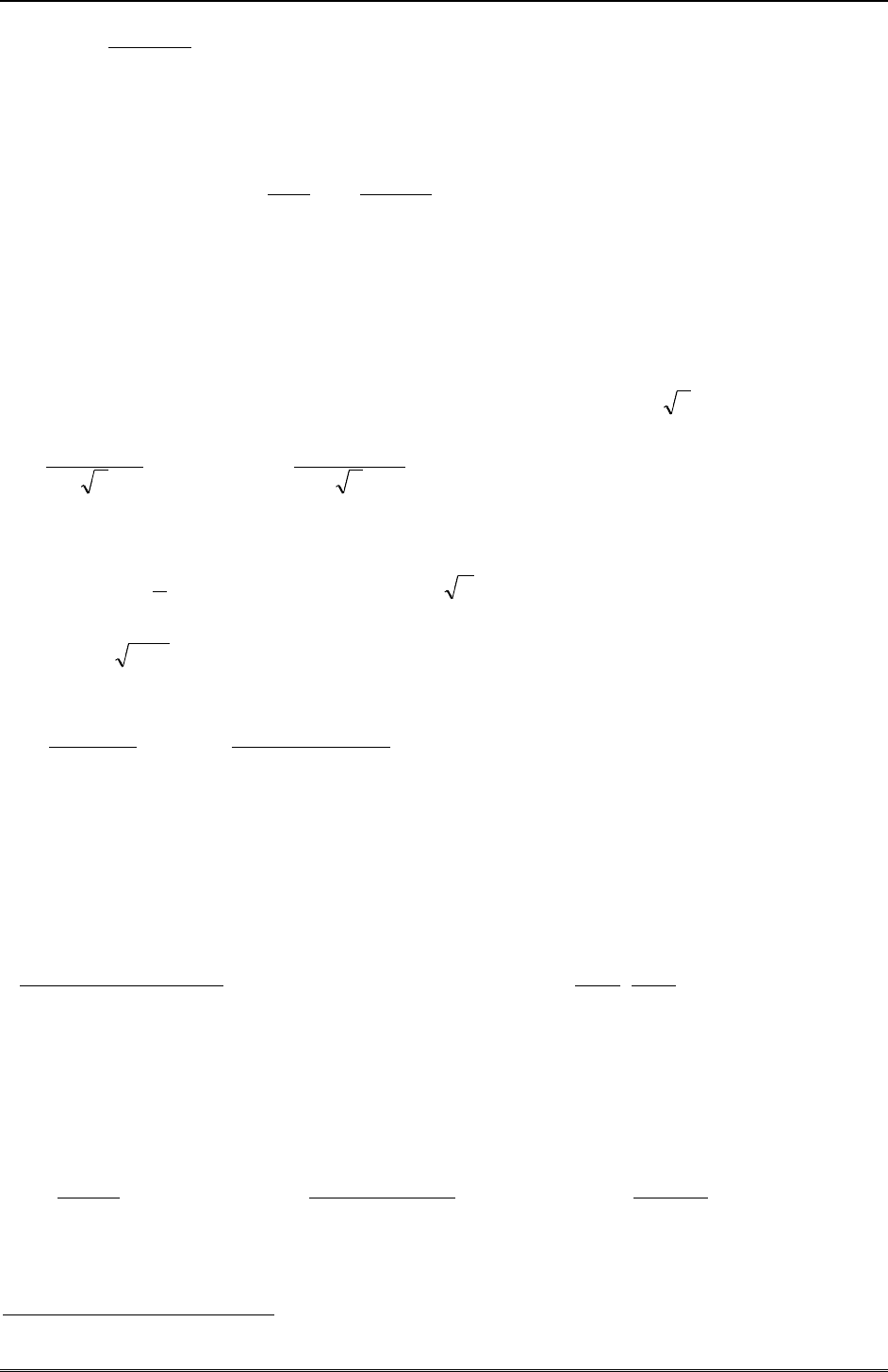
Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
22
0
1
)1(
),( du
u
u
baB
ba
a
.
В частном случае
ab 1
, бета-функция выражается через так называемый интеграл Эй-
лера
)sin(1
)1()()1,(
0
1
a
du
u
u
aaaaB
a
.
Это частное значение бета-функции также желательно запомнить. Другие конкретные
значения гамма и бета-функции можно найти в соответствующих справочниках.
11
Пример 1. Вычислить интеграл Гаусса
0,)2exp(
2
adxbxaxG
.
Выделяя в показателе экспоненты полный квадрат и делая замену
ubax
, получаем
0
2
2
2
2
)exp(
)/exp(2
)exp(
)/exp(
duu
a
ab
duu
a
ab
G
.
Получившийся интеграл сводим к гамма-функции заменой
tu
2
:
2/2/)2/1()exp(
2
1
)exp(
0
2/1
0
2
dtttduu
.
Ответ:
)/exp(/
2
abaG
.
Пример 2. Вычислить интегралы, установив, при каких значениях параметра они сходятся
А)
0
)cos(1
)(sin
dx
x
x
p
, Б)
2/
0
2
))cos()(sin(
)(tg
dx
xx
x
p
.
А) Вблизи границ интервала интегрирования подынтегральная функция
p
x
xxf
0
)(
,
2/)()(
2
p
x
xxf
. Для сходимости интеграла требуется выполнение условий:
12,1 pp
. Следовательно, интеграл сходится при
1p
. Переходя к переменной
tx 2/
, сведем интеграл к бета-функции:
2
1
,
2
1
2)(sin)(cos2
)2/(cos2
))2/sin()2/cos(2(
1
2/
0
21
0
2
pp
dtttdx
x
xx
pppp
p
.
Б) Вблизи границ интервала интегрирования подынтегральная функция
p
x
xxf
0
)(
,
p
x
xxf
)2/()(
2/
. Для сходимости интеграла требуется выполнение условия
1|| p
.
Заменой
tx )tg(
, сводим интеграл к бета-функции:
)sin(
)1()(
)2(
)1()1(
)1,1(
)1(
0
2
p
p
ppp
pp
ppdt
t
t
I
p
.
11
Справочник по специальным функциям. (под редакцией М. Абрамовица и И. Стигана), М., Наука, 1979,
является одним из лучших.
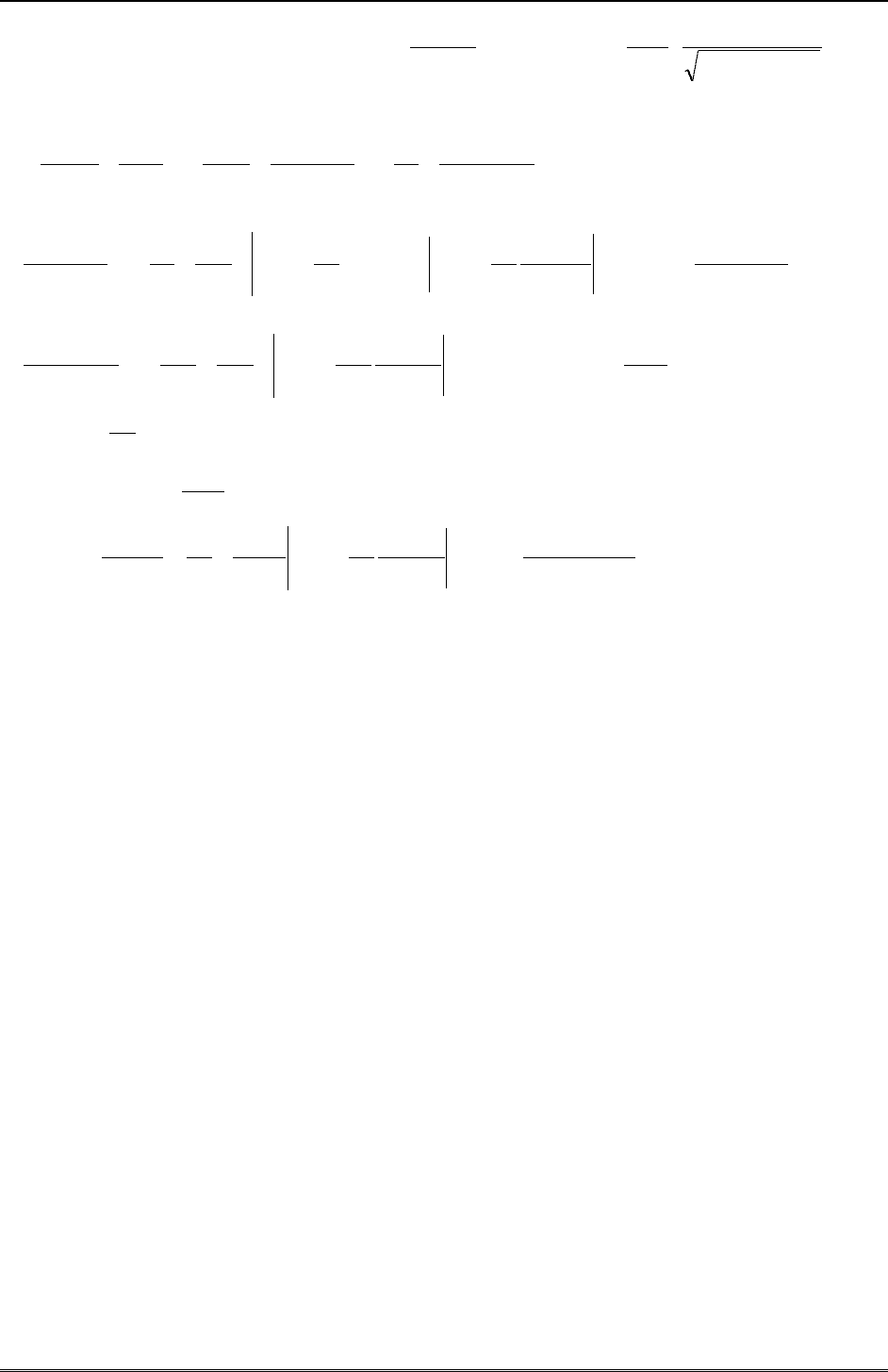
Техника дифференцирования и интегрирования
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
23
Пример 3. Вычислить интегралы А)
0
22
2
)(ln
dx
ax
x
I
, Б)
1
1
3
2
)1()1(
1
1
ln
xx
dx
x
x
J
.
А) Делаем замену переменной
tax
22
/
, и разбиваем интеграл на сумму трех слагаемых
.
1
)(ln
8
1
1
)ln()ln(
12
)(ln
12/12
0
12/1
0
12/12
dt
t
tt
a
dt
t
tt
a
a
dt
t
t
a
a
I
Вычисляем получившиеся интегралы сведением к интегралу Эйлера:
.0
)2/(sin
)2/cos(
)sin(
)1,(
11
)ln(
2
2
2/1
2/1
2/1
0
1
0
12/1
b
b
b
b
bdb
d
bb
db
d
dt
t
t
db
d
dt
t
tt
2
2/1
2
2
2/1
0
1
2
2
0
12/12
)sin(11
)(ln
b
b
b
bdb
d
dt
t
t
db
d
dt
t
tt
,
)2/1,2/1(
1
0
12/1
du
t
t
.
Ответ:
4/)(ln
2
22
a
a
I
.
Б) Делаем замену
t
x
x
1
1
, тогда
3/2
)3/(sin
)3/cos(
)sin()1()1(
)ln(
2
2
2
3/1
3/1
0
1
0
13/1
b
b
b
bdb
d
t
dtt
db
d
t
dtt
tJ
.

Кафедра высшей математики КузГТУ Конспекты проф. Д.В. Алексеева
Функции комплексной переменной. Начальные сведения
Одним из важнейших результатов теории функций одной переменной является формула
Ньютона – Лейбница, связывающая между собой понятия производной, первообразной и
определенного интеграла. Этот результат можно кратко резюмировать формулами:
)()()( aFbFdxxf
b
a
,
),(),()( baxxfxF
.
Проводимое ниже построение теории функций комплексной переменной будет основы-
ваться на идее обобщения данного результата на случай комплексных чисел. Как будет
видно из дальнейшего, проводимое таким образом построение теории функций комплекс-
ной переменной опирается на понятие потенциального векторного поля на плоскости.
Комплексные числа
Алгебраическая форма комплексных чисел
Комплексными числами называются упорядоченные пары вещественных чисел
),( yxz
.
Первое число пары называется действительной частью комплексного числа, а второе
число пары, - мнимой частью комплексного числа. Их обозначают символами
zx Re
и
zy Im
соответственно. Сложение и вычитание комплексных чисел, определяются пра-
вилом
),(
212121
yyxxzz
, а умножение комплексного числа на вещественное число, -
по правилу
),( ayaxaz
.
Перечисленные действия над комплексными числами подобны линейным операциям над
векторами на плоскости. Эта схожесть между комплексными числами и векторами также
используется для наглядного представления комплексных чисел точками на плоскости,
называемой комплексной плоскостью, по правилу:
zRe
- абсцисса,
zIm
- ордината.
В отличие от векторов, над комплексными числами определена единственная операция
умножения, сопоставляющая паре комплексных чисел другое комплексное число по пра-
вилу
),(
2121212121
xyyxyyxxzz
.
Из этого определения непосредственно видно, что произведение комплексных чисел не
зависит от порядка сомножителей.
Среди всего множества комплексных чисел выделяют следующие подмножества и специ-
альные комплексные числа
Подмножество действительных чисел
)0,(x
Подмножество мнимых чисел
),0( y
Комплексный нуль
)0,0(
Мнимая единица
)1,0(i
Из правила перемножения комплексных чисел следуют правила вычисления натуральных
степеней мнимой единицы
1
2
i
,
nn
i )1(
2
,
ii
nn
)1(
12
,
а также представление комплексного числа при помощи операций сложения и умножения
по формуле
yixz
.
Функции комплексной переменной. Начальные сведения
Кафедра высшей математики КузГТУ Конспекты проф. Д.В. Алексеева
2
В такой записи действительные и мнимые числа представляются в виде
0 ixz
и
yiz 0
соответственно, мнимая единица
10 i
, а комплексный нуль
00 i
,
1
а опи-
санные выше арифметические действия над комплексными числами, выполняются по
формулам
)()()()(
2121221121
yyixxyixyixzz
,
yaixaza
,
)()()()(
21212121221121
xyyxiyyxxyixyixzz
,
то есть при помощи обычных алгебраических правил раскрытия скобок и группировки, а
единственным новым моментом являются правила возведения мнимой единицы в степень.
При этом для суммирования и перемножения произвольного конечного набора комплекс-
ных чисел можно использовать обычные алгебраические правила, включая формулы со-
кращенного умножения, бином Ньютона, формулы суммирования прогрессий и т. п.
Над комплексными числами определена особая операция, называемая комплексное со-
пряжение, - действие, сопоставляющее исходному числу, другое комплексное число по
правилу
yixzyixz
, то есть комплексное сопряжение меняет знак мнимой
части исходного числа (комплексное сопряжение обычно обозначают чертой сверху).
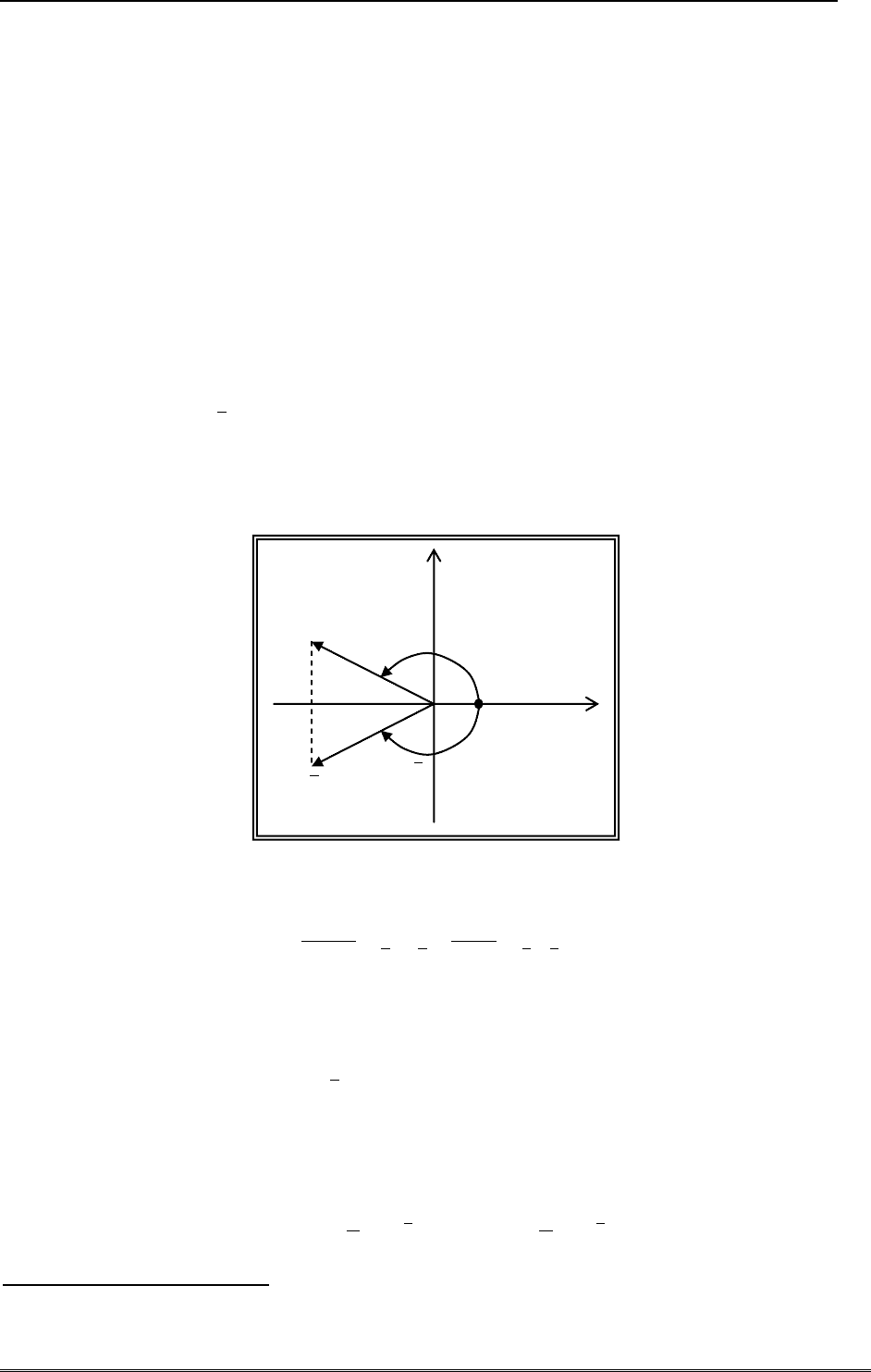
С точки зрения изображения комплексных чисел на плоскости, комплексное сопряжение
связывает между собой числа, симметричные относительно оси абсцисс (рис. 1).
Рисунок 1. Пара комплексно-сопряженных чисел на комплексной плоскости
Из правил сложения и умножения комплексных чисел следует, что справедливы равенства
2121
zzzz
,
2121
zzzz
.
Кроме того, из формулы умножения комплексных чисел следует, что произведение ком-
плексно сопряженной пары чисел дает неотрицательное действительное число, называе-
мое квадратом модуля комплексного числа
222
)()(|| yxyixyixzzz
.
При этом единственным числом с нулевым модулем является комплексный нуль. Из пра-
вил сложения и умножения комплексных чисел получаются формулы для выделения дей-
ствительной и мнимой части комплексного числа
)(
2
1
Re zzxz
,
)(
2
1
Im zziz
.
1
Комплексный нуль для краткости обозначают как обычный нуль, поэтому, работая с формулами, содер-
жащими комплексные числа необходимо понимать, где они содержат комплексный нуль, а где обычный
нуль.
zarg
zarg
z
z
zRe
zIm
