Алексеев Д.В. Конспекты по общему курсу математики
Подождите немного. Документ загружается.

Функции одной переменной. Начальные сведения
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
8
ax
ax
xxafxf
0|)(|),()()(
.
Определение дифференцируемой функции выделяет во всем множестве непрерывных
функций важнейший класс функций, называемых дифференцируемыми функциями, путем
уточнения структуры бесконечно малой функции в последней формуле. Поэтому, любая
дифференцируемая функция является непрерывной функцией, а обратное утверждение
неверно, - не всякая непрерывная функция дифференцируемая.
Определение дифференцируемой функции и производной
Функция
)(xf
называется дифференцируемой в точке
ax
, если вблизи этой точки она
может быть представлена в виде
axoaxafafxf
ax
))(()()(
.
Входящая в данную формулу константа, обозначенная символом
)(af
, называется произ-
водной функции в рассматриваемой точке
ax
.
Непосредственно из определения дифференцируемой функции следует приближенная
формула для оценки производной в виде частного приращения функции
)()( afxff
и приращения аргумента
axx
ax
afxf
o
ax
afxf
af
)()(
1
)()(
)(
.
Приближенное значение производной тем точнее, чем меньше приращение
x
.
Поскольку
0)1(lim
o
ax
, из определения дифференцируемой функции получается и точная
формула, выражающая производную в точке через предельное значение отношения при-
ращения функции к приращению переменной:
ax
afxf
af
ax
)()(
lim)(
.
Отсюда сразу получаются три простых, но важных результата:
производная постоянной функции
ConstCxf )(
равна нулю (
0f
);
производная тождественной функции
xxf )(
равна единице (
axf
),
производная степени с натуральным показателем
1
)(
nn
xnx
2
.
Множество всех значений переменной, при которых рассматриваемая функция является
дифференцируемой, называется областью существования производной. Поэтому естест-
венно рассматривать функцию, сопоставляющую значениям переменной из области суще-
ствования производной значения производной рассматриваемой функции в этой точке
)(xfx
. Именно эту функцию и называют производной исходной функции
)(xf
.
Практическое вычисление производных основано либо на определении дифференцируе-
мой функции, либо на следствиях этого определения, называемых правилами дифферен-
цирования. Ниже будут использоваться оба эти приема вычисления производных. Вычис-
ление по определению дифференцируемой функции будет использоваться для получения
2
Для получения этой формулы достаточно вспомнить формулу суммы геометрической прогрессии
1123221
n
ax
nnnnn
nn
naaxaxaaxx
ax
ax
.

Функции одной переменной. Начальные сведения
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
9
базового справочного набора производных, а правила дифференцирования, - как основной
способ вычисления производных.
Дифференциал, касательная к графику и геометрический смысл дифференцирования
Дифференциалом функции в точке
ax
называется линейная часть ее приращения
))(( axafdf
.
Поскольку дифференциал тождественной функции
axdx
, дифференциал принято за-
писывать в виде
dxafdf )(
.
3
Рассмотрим линейную функцию
))(()( axafafy
, определяемую дифференциалом.
Ее графиком является прямая линия, проходящая через опорную точку
))(,( afa
, а коэф-
фициент наклона этой прямой определяется отношением приращений
xy /
и равен
производной функции в опорной точке
)(
)(
af
ax
afy
x
y
.
Сравнение данного уравнения с уравнением прямой, пересекающей график функции в
двух точках
))(,( afa
,
))(,( bfb
(с уравнением секущей)
)(
)()(
)( ax
ab
afbf
afy
,
показывает, что уравнение секущей переходит в уравнение прямой, определяемой диффе-
ренциалом в предельном режиме
ab
.
Поскольку с геометрической точки зрения, этот предельный переход соответствует пере-
ходу секущей в касательную, справедливо утверждение: операция дифференцирования
сопоставляет каждой точке графика дифференцируемой функции
))(,( xfx
касательную
к графику, проходящую в направлении, задаваемом вектором с координатами
))(,1( xf
,
при этом, координаты вектора, направленного вдоль касательной, получаются диффе-
ренцированием координат вектора, задающего точку на графике функции.
В этом и состоит геометрический смысл операции дифференцирования функции (см. ри-
сунок 1).
3
Из этой формулы следует обозначение производной по Лейбницу, выражаемое словами: «Производная
равна отношению дифференциалов
dx
df
xf
)(
», а также использованный выше символ операции диффе-
ренцирования
dx
d
, называемый оператором дифференцирования.

Функции одной переменной. Начальные сведения
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
10
Рисунок 1 Геометрический смысл дифференцирования. Переход секущей в касательную (слева)
и касательный вектор к графику (справа).
Первообразная и неопределенный интеграл
Функция
)(xF
называется первообразной по отношению к функции
)(xf
, если она удов-
летворяет условию
)()( xfxF
на всей области определения
)(xf
.
Пусть
)(xF
первообразная, тогда
axoaxafaFxF ))(()()(
. Рассмотрим функ-
цию
CxFxF
c
)()(
, отличающуюся от
)(xF
постоянным слагаемым. Поскольку
axoaxafCaFCxF ))(()()(
обе функции
)(),( xFxF
c
, являются первообраз-
ными
)(xf
. Следовательно, задача об отыскании первообразной имеет бесконечное мно-
жество решений, любая пара которых различается лишь на постоянное слагаемое.
Множество всех первообразных рассматриваемой функции называется неопределенным
интегралом функции
)(xf
и обозначается символом
dxxf )(
. Операция нахождения пер-
вообразной называется интегрированием. Символ интеграла
dx
используется для обо-
значения этой операции, а функция,
)(xf
находящаяся под знаком интеграла называется
подынтегральной функцией. Решение задачи об отыскании первообразной принято запи-
сывать в виде
CxFdxxf
)()(
,
а взаимосвязь неопределенного интеграла с подынтегральной функцией, - в виде
)()( xfdxxf
, или
)()( xfdxxf
dx
d
.
Практическое выполнение интегрирования основано на некотором базовом справочном
наборе первообразных и правилах интегрирования, являющихся утверждениями, обрат-
ными правилам дифференцирования. Заметим, что если для выполнения дифференциро-
вания достаточно просто знать некоторый базовый набор производных и следовать прави-
лам дифференцирования, то в интегрировании далеко не последнюю роль играет метод
проб и ошибок, полного или частичного угадывания результата с дальнейшей его провер-
кой или обоснованием.
4
4
Принципиальное различие между умением дифференцировать и интегрировать отражено даже в анекдо-
тах. Вопрос: «Чем дифференцирование отличается от интегрирования?». Ответ: «Дифференцировать можно
научить даже обезьяну, а вот интегрировать ее в принципе научить нельзя!»
))(,( afa
))(,( bfb
ab
))(,( afa
))(,1( afV

Функции одной переменной. Начальные сведения
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
11
Правила дифференцирования и интегрирования
Правилами дифференцирования называются правила вычисления производных функций,
получаемых при помощи операций сложения, умножения и композиции из функций, про-
изводные которых известны. То есть, при получении этих правил, мы опираемся на опре-
деление дифференцируемости пары функций
axoaxafafxf
ax
))(()()(
,
axoaxagagxg
ax
))(()()(
.
Правилами интегрирования называются правила нахождения первообразных, получаемые
путем обращения правил дифференцирования.
Дифференцирование и интегрирование линейной комбинации функций
Линейной комбинацией двух функций
)(),( xgxf
называется функция, построенная по
формуле
)()( xgBxfA
, где
BA,
– действительные константы. Подставляя в линейную
комбинацию условия дифференцируемости рассматриваемых функций, получаем
)))(()(()))(()(()()( axoaxagagBaxoaxafafAxgBxfA
ax
,
что после перегруппировки и сложения бесконечно малых порядка выше первого дает:
axoaxagBafAagBafAxgBxfA
ax
)))(()(()()()()(
.
Производная находится отсюда как коэффициент при приращении аргумента, то есть
)()())()(( xgBxfAxgBxfA
.
Это и есть правило вычисления производной линейной комбинации двух функций.
Частными случаями данного правила являются правила вычисления производной суммы и
разности двух функций. Кроме того, данное правило непосредственно обобщается на слу-
чай линейной комбинации произвольного числа функций.
Правило интегрирования линейной комбинации двух функций получается обращением
правила дифференцирования линейной комбинации, - первообразная линейной комбина-
ции двух функций с точностью до постоянного слагаемого равна линейной комбинации
первообразных этих функций.
Более подробно. Пусть для пары функций известны их первообразные
)()( xFdxxf
,
)()( xGdxxg
.
Тогда обращение правила вычисления производной линейной комбинации
)()())()(( xGBxFACxGBxFA
,
дает следующее правило интегрирования
dxxgBdxxfAdxxgBxfA )()())()((
.
Это и есть правило интегрирования линейной комбинации пары функций. Частным случа-
ем данного правила являются правила интегрирования суммы и разности двух функций.
Кроме того, данное правило непосредственно обобщается на линейную комбинацию про-
извольного числа функций.
Дифференцирование произведения функций и формула интегрирования произведения
Перемножая равенства, определяющие дифференцируемость
)(),( xgxf
, получаем

Функции одной переменной. Начальные сведения
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
12
axoaxoaxoaxagafaxoafag
axagafagafagaf
axoaxagagaxoaxafafxgxf
ax
)))(()(())()((
)))(()()()(()()(
)))(()(()))(()(()()(
Нетрудно заметить, что три последних слагаемых в правой части равенства имеют поря-
док малости выше первого. Производную получаем по линейной части приращения, то
есть правило дифференцирования произведения имеет вид:
)()()()())()(( xgxfxgxfxgxf
.
Обращение этого правила, совместно с линейностью операции интегрирования, дает фор-
мулу интегрирования произведения
dxxgxfdxxgxfxgxf )()()()()()(
,
которую также называют формулой интегрирования по частям. Эта формула использует-
ся для того, чтобы подходящим выбором функций
)(),( xgxf
свести исходный интеграл к
более простому интегралу, следуя формуле
dxxgxfxgxfdxxgxf )()()()()()(
.
Примеры применения этого приема будут приведены в соответствующем разделе.
Дифференцирование композиции функций и формула интегрирование подстановкой
Композицией функций, которая также называется сложной функцией, называется функ-
ция, получаемая путем «встраивания» формулы одной функции внутрь формулы другой
функции
))(( xgfy
. Для разбора структуры сложной функции лучше использовать
стрелочные обозначения, в которых четко видна последовательность вычислений значе-
ний сложной функции
)()( tfyxgtx
.
Из этого обозначения четко видна не только последовательность вычисления, но и все
формулы, по которым проводится вычисление вспомогательных промежуточных пере-
менных. Это особенно удобно, когда композицию образуют три и более функций.
Рассмотрим композицию дифференцируемых функций
gf ,
вблизи точки
ax
)()( tfyxgtx
,
)()( bfyagba
.
Из формул
btobtbfbftf
bt
))(()()(
,
axoaxagagxg
ax
))(()()(
,
получаем
axOaxoaxagbt
ax
))((
,
axoaxagbfbfaxOoaxagbfbftf
bt
))(()()())(()()()(
,
откуда формула для производной находится по линейной части приращения.
Таким образом, правило вычисления производной сложной функции имеет вид
)(),()())((( xgtxgtfxgf
.
Мы не выделяем отдельно правило вычисления производной частного, так как это просто
комбинация правил вычисления производной произведения и сложной функции:
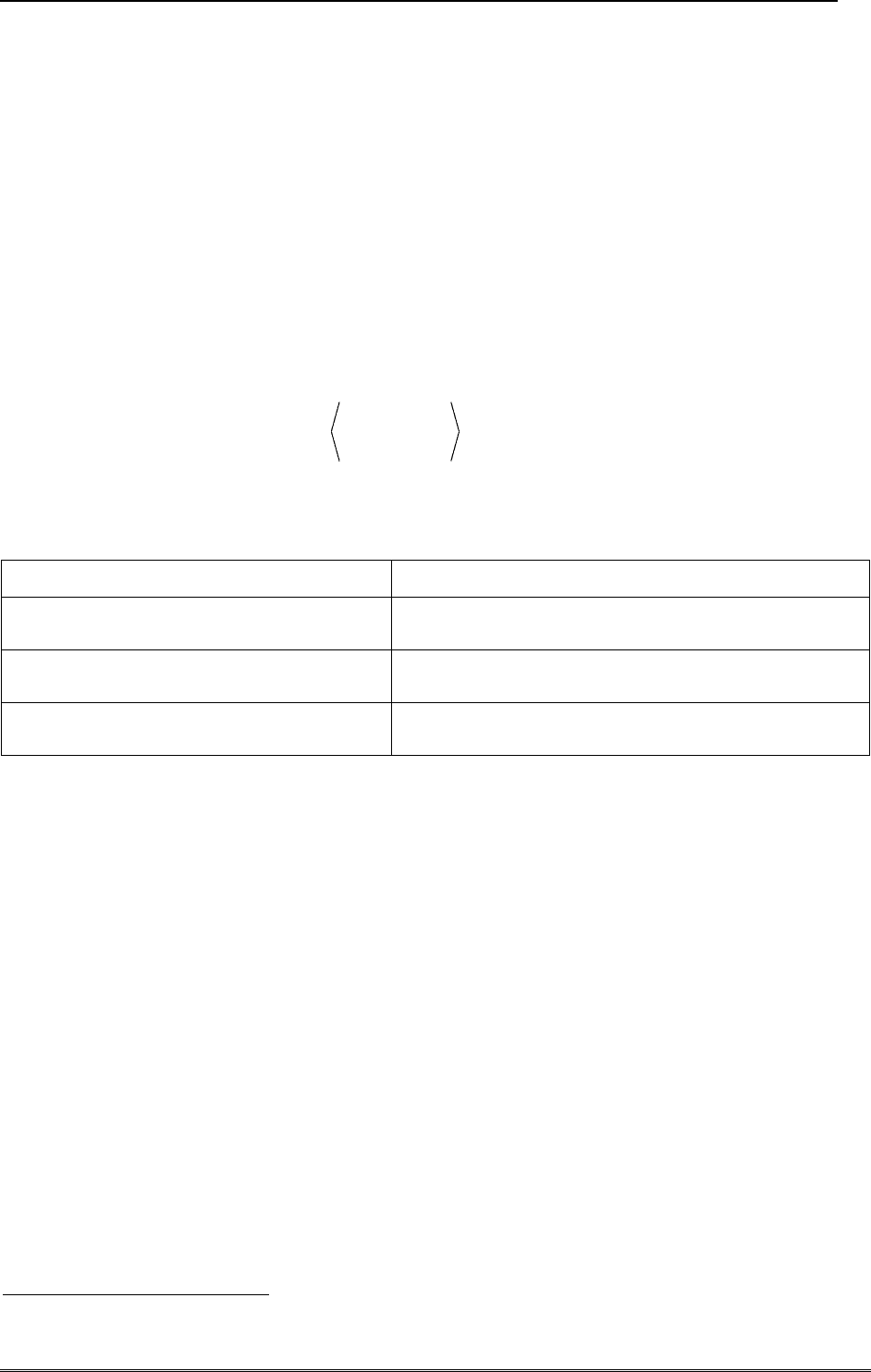
Функции одной переменной. Начальные сведения
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
13
))(()()()())()(())(/)((
111
xgxfxgxfxgxfxgxf
,
)()()()())(()(
2111
xgxgxgtxgtxgtx
,
5
)()()()()())(/)((
21
xgxgxfxgxfxgxf
.
Для приведения данной формулы к привычному виду достаточно привести ее правую
часть к общему знаменателю.
Правило интегрирования, обратное к правилу дифференцирования сложной функции на-
зывается интегрированием подстановкой или подведением под дифференциал.
Пусть известна первообразная
dttftF )()(
, тогда из формулы
)())(()())(()))((( xgxgfxgxgFxgF
следует правило интегрирования подведением под дифференциал
))(()()(
)(
),(
)())(( xgFtFdttf
dxxgdt
xgt
dxxgxgf
.
Сводка описанных выше трех основных правил дифференцирования и соответствующих
им правил интегрирования приведена в таблице 3.
Таблица 3 Взаимосвязь правил дифференцирования и интегрирования
Правило дифференцирования
Правило интегрирования
)()())()(( agBafAxgBxfA
dxxgBdxxfAdxxgBxfA )()())()((
)()()()())()(( xgxfxgxfxgxf
dxxgxfxgxfdxxgxf )()()()()()(
)(),()())((( xgtxgtfxgf
))(()())(()()( xgFdxxgxgftFdttf
Определенный интеграл и формула Ньютона - Лейбница
Определенный интеграл как площадь
Определенный интеграл от непрерывной функции по конечному интервалу, обозначаемый
символом
b
a
dxxf )(
,
проще всего определить как «площадь» фигуры, заключенной между осью абсцисс и гра-
фиком функции.
6
Слово «площадь» взято в кавычки, так как при ее вычислении учитывает
знак функции. Вклад в «площадь» имеет положительный знак, если график расположен
выше оси абсцисс и отрицательный знак, если график расположен ниже оси абсцисс.
Для вычисления площади рассматриваемый интервал
),( ba
разбивают на большое число
N
интервалов малой длины
Nabx /)(
и в каждом из этих интервалов
),(
1jj
xx
, на-
ходят наибольшее
)(
max
jf
и наименьшее
)(
min
jf
значение функции (здесь
xjax
j
,
1,2,1,0 Nj
).
5
Формулу
21
)(
tt
получается по определению
)/())(/()()(
211
ttttttttt
.
6
Эту фигуру называют криволинейной трапецией.
Функции одной переменной. Начальные сведения
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
14
В результате определенный интеграл оценивается неравенствами
max
1
0
max
1
0
minmin
)()()( IjfxdxxfjfxI
N
j
b
a
N
j
.
Входящие в это неравенство суммы
max
1
0
minmin
)(
N
j
jfxI
,
1
0
maxmax
)(
N
j
jfxI
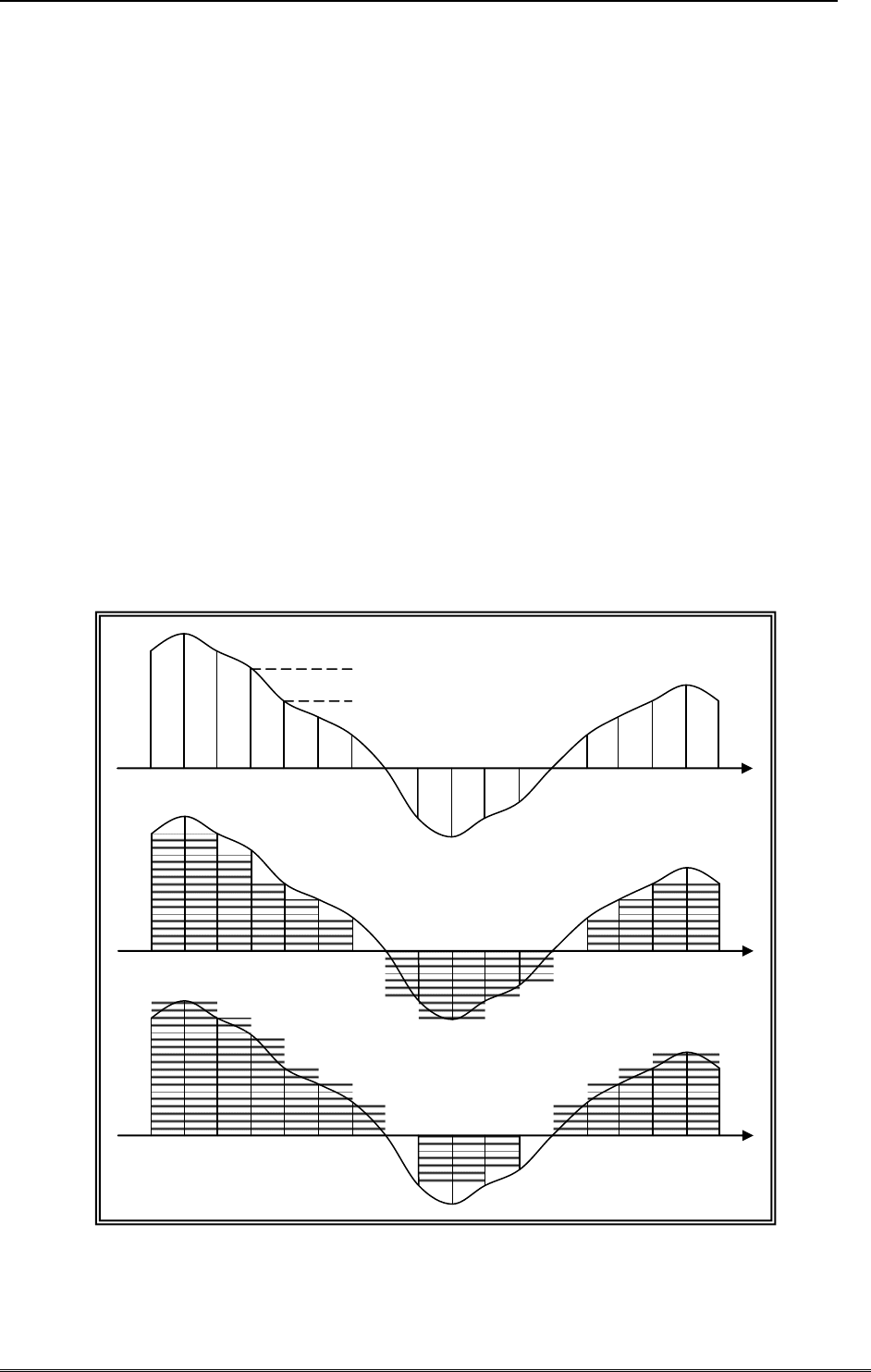
имеют простой геометрический смысл, - они дают приближенную оценку площади криво-
линейной трапеции в виде суммы площадей прямоугольников, «заполняющих» криволи-
нейную трапецию снизу и «накрывающих» ее сверху (рисунок 2). При этом точность при-
ближения площади криволинейной трапеции суммой площадей прямоугольников тем
точнее, чем меньше длина интервала разбиения
Nabx /)(
, то есть чем больше число
интервалов. Для доказательства этого факта покажем, что нижняя и верхняя границы
maxmin
,II
сближаются в пределе
)(,0 Nx
.
Так как подынтегральная функция является непрерывной, то
0|)()(|
0
minmax
x
jfjf
, тогда
01)1()()1(1|)()(|||
0
1
0
0
1
0
minmaxminmax
x
N
j
x
N
j
ooaboxNoxjfjfxII
.
Рисунок 2 Разбиение интервала интегрирования и приближение площади криволинейной трапеции
суммой площадей нижних (в середине) и верхних прямоугольников
При фиксированной нижней границе интервала интегрирования определенный интеграл
можно рассматривать как функцию верхней границы интервала интегрирования
1kk
xx
)(
)(
min
max
kf
kf
a
b

Функции одной переменной. Начальные сведения
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
15
x
a
dzzfxS )()(
.
Рассмотрим приращение этой функции при малом изменении положения верхней границы
)()()( xSxxSxS
.
Точное значение приращения удовлетворяет неравенству
xffxxfxS |||)()(|
minmax
,
)(max
),(
max
xff
xxxx
)(min
),(
min
xff
xxxx
.
Так как в силу непрерывности подынтегральной функции
0||
0
minmax
x
ff
, произведе-
ние
xoxff ||
minmax
. Отсюда следует, что
)()()()( xoxxfxSxxS
то есть определенный интеграл как функция верхней границы интегрирования является
первообразной для подынтегральной функции
)()( xfxS
.
Другими словами, производная определенного интеграла от непрерывной функции по
верхней границе интегрирования равна значению подынтегральной функции на этой гра-
нице
f x
d
dx
f z dz
a
x
( ) ( )
.
Этот результат носит название основной теоремы математического анализа для непре-
рывных функций, поскольку он связывает между собой все основные понятия анализа, -
определенный интеграл, производную и первообразную.
Формула Ньютона - Лейбница
Пусть
)(xF
любая другая первообразная подынтегральной функции. Поскольку различ-
ные первообразные одной функции различаются лишь на постоянное слагаемое, то спра-
ведливо равенство
CdzzfxF
x
a
)()(
.
Условие обращения в нуль определенного интеграла по интервалу нулевой длины позво-
ляет определить входящую в данную формулу неизвестную константу
C
при помощи
подстановки значения переменной
ax
)(,)()( aFCCdzzfaF
a
a
.
Отсюда сразу следует, что определенный интеграл по интервалу
),( ba
равен разности
значений любой первообразной подынтегральной функции на границах интервала интег-
рирования
f x dx F b F a
a
b
( ) ( ) ( )
.
Последняя формула носит название формулы Ньютона-Лейбница.
Замечание. Разность функций, принято обозначать символом
)()()( aFbFxF
b
a
.

Функции одной переменной. Начальные сведения
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
16
Из формулы Ньютона-Лейбница легко получить следующие важные свойства определен-
ного интеграла
Определенный интеграл меняет знак при перестановке границ интегрирования
f x dx f x dx
a
b
b
a
( ) ( )
Определенный интеграл аддитивная функция интервалов интегрирования
b
c
c
a
b
a
dxxfdxxfdxxf )()()(
Из свойства нечетности определенного интеграла при перестановке границ интегрирова-
ния сразу получается следующее дополнение к основной теореме анализа:
Производная определенного интеграла от непрерывной функции по нижней границе ин-
тегрирования равна значению подынтегральной функции на этой границе с обратным
знаком
a
x
dzzf
dx
d
xf )()(
.
В заключении рассмотрим определение определенного интеграла в виде суммы с точки
зрения формулы Ньютона – Лейбница. Выполняя разбиение интервала интегрирования на
малые интервалы равной длины, так как это было сделано выше, запишем определенный
интеграл в виде суммы
1
0
1
)}()({)(
N
k
kk
b
a
xFxFdxxf
.
Поскольку отдельный вклад в сумму
)()()()(
1
xoxxfxFxF
kkk
, получаем
)1()()()())()(()(
1
0
1
0
1
0
oxxfxoNxxfxoxxfdxxf
N
k
k
N
k
k
N
k
k
b
a
.
Поскольку
01lim
0
o
x
, определенный интеграл от непрерывной функции можно опреде-
лить как предел
xabNxxfdxxf
N
k
k
x
b
a
/)(,)(lim)(
1
0
0
Входящая в последнее равенство сумма, называется интегральной суммой. При конечных
значениях числа слагаемых интегральная сумма дает приближенную оценку определенно-
го интеграла в виде суммы «площадей прямоугольников», «высота» которых определяется
значениями функции
)(
k
xf
, а ширина основания равна
x
. Эта оценка тем точнее, чем
меньше длина интервала разбиения
x
.
Понятие интегральной суммы принципиально важно с точки зрения приложений. Именно
правильная формула элементарного вклада в суммируемую характеристику
xxf
k
)(
оп-
ределяет успешное вычисление суммарной характеристики, задаваемой определенным
интегралом.

Функции одной переменной. Начальные сведения
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
17
Представление функций степенными рядами
Формула Тейлора и ряд Тейлора
Определение производных высшего порядка
Так как производная некоторой функции
)(xf
сама является функцией, можно поставить
вопрос о ее дифференцируемости. Если производная дифференцируемая функция, то ее
производная называется второй производной или производной второго порядка по отно-
шению к исходной функции. Поскольку понятие второй производной основано на данном
ранее определении дифференцируемой функции, ясно, что вычисление второй производ-
ной проводится по тем же самым правилам дифференцирования.
Далее можно поставить вопрос и о дифференцируемости второй производной и прийти к
понятию производной третьего порядка (третьей производной). Этот процесс можно про-
должать до тех пор, пока будут получаться дифференцируемые функции. Таким образом,
мы приходим к следующему определению производных высшего порядка.
Производная порядка
n
это функция
)(
)(
xf
n
, получающаяся путем
n
- кратного диффе-
ренцирования исходной функции
)(xf
.))(()(,))(()(,))(()(
)1()()3(
xfxfxfxfxfxf
nn
Вывод формулы Тейлора при помощи формулы интегрирования произведения
Рассмотрим формулу, представляющую функцию через ее производную по формуле Нью-
тона – Лейбница и применим формулу интегрирования произведения несколько раз по
описанной ниже схеме (штрих обозначает дифференцирование по переменной
t
)
7
x
a
x
a
dttftxafdttfafxf )()()()()()(
,
x
a
x
a
x
a
dttftxtftxafdttftxafxf )()()()()()()()()(
,
x
a
x
a
x
a
x
a
dttftxtftxdttftxdttftx )()(
2
1
)()(
2
1
)())((
2
1
)()(
)3(222
,
x
a
x
a
x
a
x
a
dttftxtftxdttftxdttftx )()(
32
1
)()(
32
1
)())((
32
1
)()(
2
1
)4(3)3(3)3(3)3(2
,
,
x
a
nn
x
a
nn
x
a
nn
x
a
nn
dttftx
n
tftx
n
dttftx
n
dttftx
n
)()(
!
1
)()(
!
1
)())((
!
1
)()(
)!1(
1
)1()()()(1
.
Применение формулы интегрирования произведения продолжается до тех пор, пока по-
вторное дифференцирование функции
)(xf
является допустимым.
Объединяя полученные формулы, получаем так называемую формулу Тейлора, которая
раскрывает смысл бесконечно малой
axo
в определении дифференцируемой функции
7
При получении выписанных ниже формул использовалась формула для производной степени с натураль-
ным показателем.
