Алексеев Д.В. Конспекты по общему курсу математики

Подождите немного. Документ загружается.

Начальные сведения о дифференциальных уравнениях

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

тинную фазовую траекторию, то есть насколько хорошо (с какой точностью?) выполняет-

ся приближенное равенство

)(

txx





на всех узлах временной сетки.

Таким образом, задача о нахождении численного решения обыкновенного дифференци-

ального уравнения может быть сформулирована в следующем виде: по известному диф-

ференциальному уравнению построить рекуррентное уравнение, такое, что его решение

на заданном интервале времени дает приближенное решение исходного дифференциаль-

ного уравнения с заданной точностью.

Дифференциальные уравнения интегрируемые в квадратурах

Дифференциальное уравнение называется интегрируемым в квадратурах, если его реше-

ние может быть получено в явном или неявном виде при помощи конечного числа опера-

ций над элементарными функциями, включая и интегрирование. При этом решение счита-

ется полученным и в том случае, когда возникший в ходе решения интеграл не выражает-

ся через элементарные функции. Уравнения интегрируемые в квадратурах являются хотя

и узким, но важным классом дифференциальных уравнений, их достаточно подробный

перечень можно найти в соответствующих справочниках.

Ниже рассматриваются только

наиболее простые и часто встречающиеся типы уравнений данного класса.

В настоящем разделе будем использовать следующие определения:

 Дифференциальным уравнением называется уравнение, содержащее неизвестную

функцию и ее производные, а порядком дифференциального уравнения называется

порядок старшей производной, входящей в него.

 Решением дифференциального уравнения называется функция, обращающая его в

тождество.

Уравнения вида

0))(),(),(,(

)(





xyxyxyxF



называют дифференциальными уравнениями

порядка

общего вида, а уравнения вида

))(,),(),(,()(

)1()(

xyxyxyxfxy

nn 



 

, нормаль-

ной формой дифференциального уравнения порядка

. При этом одному уравнению об-

щего вида может соответствовать совокупность уравнений нормальной формы.

Приведенные определения согласуются с данными выше геометрическими определения-

ми следующим образом.

 Состояние системы задается вектором

))(,),(),((),,(

)1(

xyxyxyxxxx





 



, то

есть координаты вектора состояния задаются формулами

nkyx

,1,

)1(





 Связь между координатами вектора состояния

1





совместно с нормальной

формой исходного уравнения

))(,),(),(,()(

)1()(

xyxyxyxfxy

nn 



 

записанной в ви-

де

)),,,,(

21 nn

xxxxfx 



, задает нестационарное поле направлений по формуле

)),,,,(,,,,,(),(

21132 nnn

xxxxfxxxxxxV 







, то есть исходное уравнение является

неавтономным уравнением на

-мерном фазовом пространстве

),( xxVx







Описанная взаимосвязь между двумя определениями дифференциального уравнения на-

зывается записью дифференциального уравнения высшего порядка в виде нормальной сис-

темы дифференциальных уравнений первого порядка. Справедливо и обратное утвержде-

ние: систему

дифференциальных уравнений первого порядка можно записать в виде

одного уравнения порядка

. Эту взаимосвязь можно гибко использовать в зависимости

Смотри, например, Э. Камке. Справочник по обыкновенным дифференциальным уравнениям. – С-Пб,

«Лань», 2003.

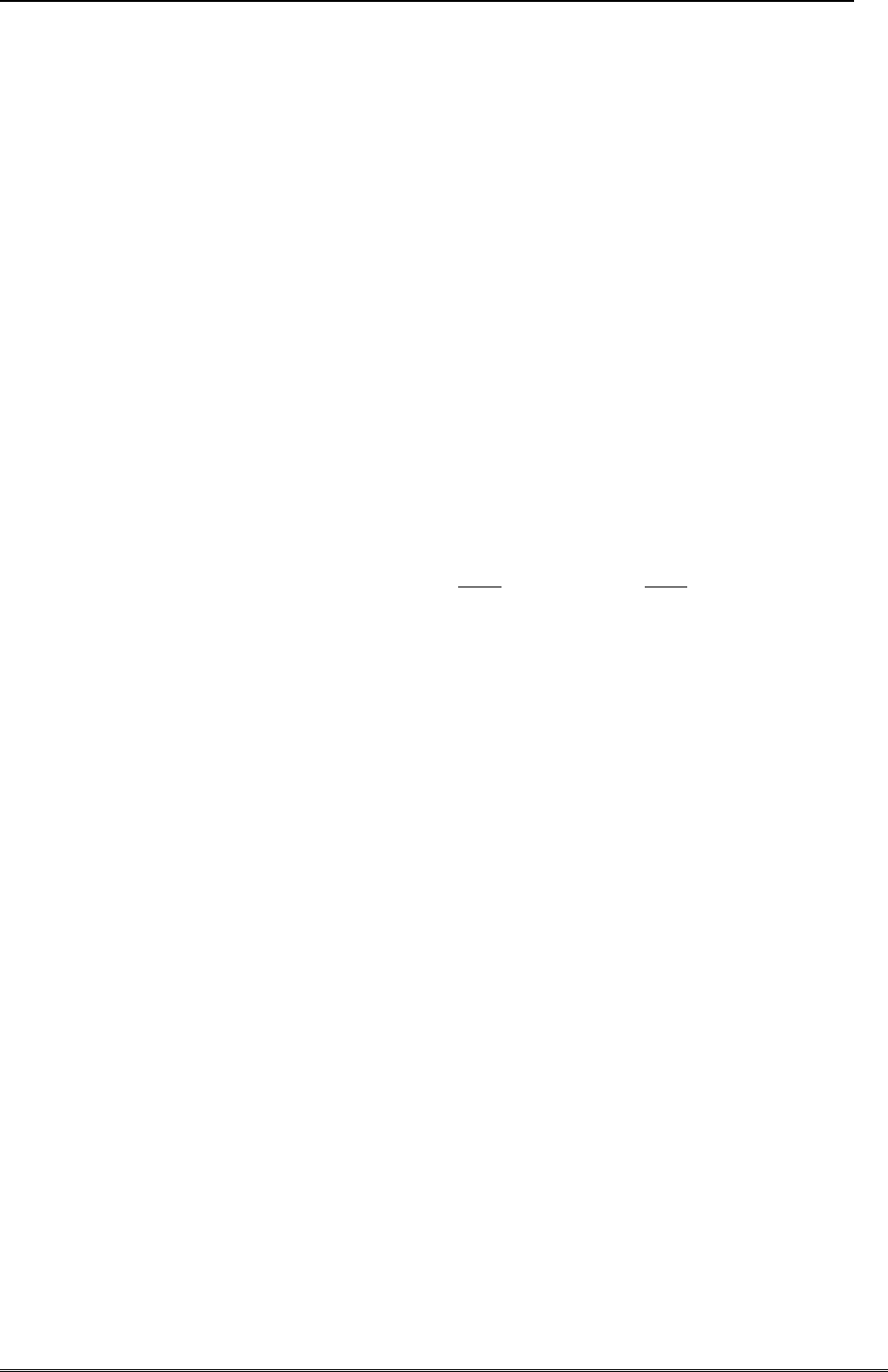
Начальные сведения о дифференциальных уравнениях

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

от особенностей конкретной задачи, - можно записать исходное уравнение в виде систе-

мы, или наоборот, исключив «лишние» переменные, записать исходную систему в виде

одного уравнения.

Стандартные дифференциальные уравнения первого порядка

Общее дифференциальное уравнение первого порядка имеет вид

0))(),(,( 



xyxyxF

, а его

нормальная форма, -

))(,()( xyxfxy 



. При записи дифференциального уравнения, аргу-

мент у функции и производной обычно опускают

),( yxfy 



Среди всех дифференциальных уравнений первого порядка выделяют стандартные типы,

для которых алгоритм получения решения известен. Рассматриваемые ниже три простей-

ших стандартных типа дифференциальных уравнений первого порядка классифицируют

по виду правой части нормальной формы уравнения

),( yxf

Уравнения с разделяющимися переменными.

Если в уравнении

),( yxfy 



функция

),( yxf

при помощи тождественных преобразова-

ний может быть переписана в виде произведения

)()(),( yhxgyxf 

, дифференциальное

уравнение называется уравнением с разделяющимися переменными. Общее решение

дифференциального уравнения с разделяющимися переменными вычисляется следующим

образом

dxxgdy

dxxgyhdyyhxgy )(

)(

)()()()( 



Cdxxgdy





)(

Последняя формула после выполнения интегрирования дает решение исходного уравне-

ния в неявном виде. Следует также, по возможности, получить и явную формулу для ис-

комого решения.

Однородные уравнения.

Если в уравнении

),( yxfy 



функция

),( yxf

при помощи тождественных преобразова-

ний может быть записана в виде

)/(),( xygyxf 

, то есть в виде функции переменной

xy/

, дифференциальное уравнение называется однородным. Однородное уравнение сво-

дится к уравнению с разделяющимися переменными при помощи следующей замены

функции

)()(



 xxyxu

. При этом при замене функции необходимо провести также и за-

мену производной

)()())(()( xuxxuxuxxy











. В результате этой замены получается

уравнение с разделяющимися переменными

)(uhuxu 





, или

))((

uuhxu 





, которое

решается, как описано выше, а конечных формулах делается обратная замена.

Линейные уравнения.

Если в уравнении

),( yxfy 



функция

),( yxf

линейна по

)()(),( xqyxpyxf 

уравнение называется линейным. В частном случае, когда

0)( xq

, линейное уравнение

0)( 



yxpy

называется однородным, а в общем случае линейное уравнение называется

неоднородным.

Важнейшим свойством линейных уравнений является то, что для них справедлив так на-

зываемый принцип суперпозиции (наложения) решений, суть которого состоит в следую-

щем. Если известны решения

)(),(

xyxy

неоднородных уравнений

)()(

111

xqyxpy 



)()(

222

xqyxpy 



, решение уравнения

)()()(

2211

xqсxqсyxpy 



, где

,сс

любые кон-

станты, выписывается по уже известным решениям по формуле

)()()(

2211

xyсxyсxy 

(доказательство принципа суперпозиции следует из линейности дифференцирования).

Начальные сведения о дифференциальных уравнениях

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Из принципа суперпозиции непосредственно следует структура общего решения линейно-

го дифференциального уравнения: общее решение линейного уравнения является суммой

общего решения однородного уравнения и частного решения неоднородного уравнения

)()()( xyxyxy



Однородное линейное уравнение

yxpy )(



является уравнением с разделяющимися пе-

ременными, и его решение получается стандартным образом:

dxxpdyy

)(





)ln()()ln( Cdxxpy





))(exp()( xPCxy



, где



 dxxpxP )()(

Частное решение неоднородного линейного уравнения вычисляется при помощи так на-

зываемого метода вариации постоянной. Идея этого метода состоит в том, что общее ре-

шение однородного уравнения подсказывает вид решения неоднородного уравнения, пу-

тем замены константы на функцию

))(exp()()( xPxAxy



. Входящая в последнюю фор-

мулу функция

)(xA

определяется из уравнения, получаемого подстановкой

)(xy

в ис-

ходное уравнение

)())(exp()()()())(exp()())(exp()( xqxPxAxpxpxPxAxPxA 



))(exp()()( xPxqxA 



, откуда функция

)(xA

находится интегрированием. Окончательно

получаем, что общее решением неоднородного линейного дифференциального уравнения

имеет вид

))(exp())(()( xPCxAxy 

, где



 dxxpxP )()(



 dxxPxqxA ))(exp()()(

Как видно из приведенных выше формул для решений уравнений с разделяющимися пе-

ременными, однородного и линейного, в формулу общего решения входит произвольная

константа, характеризующая неоднозначность операции интегрирования. Именно поэтому

эти формулы называются формулами общего решения, так как они задают семейство

функций, каждая из которых является решением исходного уравнения. Значение входя-

щей в общее решение константы фиксируется при переходе от формулы общего решения

к формуле частного решения, удовлетворяющего начальному условию

)( yxy 

, - под-

становка начального условия в формулу общего решения дает алгебраическое уравнение,

решение которого и фиксирует значение константы

Интегрирование дифференциальных уравнений заменами

переменных

Замены переменных, включающие как замену независимой переменной, так и замену ис-

комой функции часто позволяют свести исходное дифференциальное уравнение к одному

из рассмотренных выше стандартных типов дифференциальных уравнений первого по-

рядка. Все замены можно разбить на два типа:

 Замены, не изменяющие порядок исходного уравнения

 Замены, понижающие порядок исходного уравнения.

В последнем случае, вместо исходной функции вначале находится ее производная, а сама

функция находится далее интегрированием. В более сложных случаях при заменах ис-

пользуют комбинацию функции, производной и независимой переменой.

Решение дифференциальных уравнений при помощи замен переменных напоминает тех-

нику интегрирования. С одной стороны, существуют стандартные сценарии, позволяющие

свести исходное уравнение к уравнению одного из стандартных типов. С другой стороны,

для конкретного уравнения может быть использована нестандартная замена, позволяющая

получить его решение более просто. Приводимые ниже примеры иллюстрирую обе опи-

санные возможности.

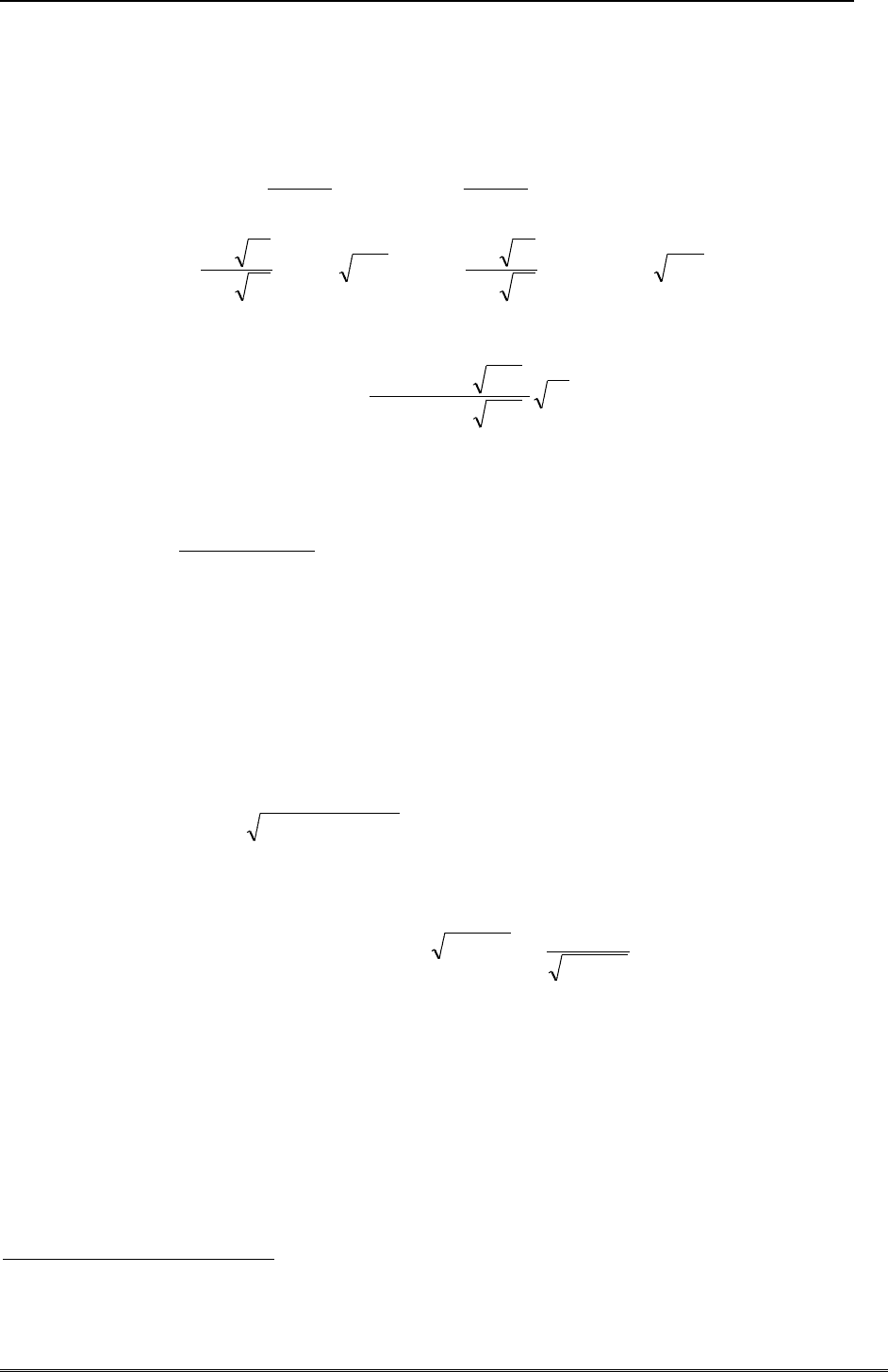
Начальные сведения о дифференциальных уравнениях

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Пример. Падение частицы при наличии квадратичной по скорости силы сопротивления.

Требуется решить уравнение

glxx  /



с начальным условием

0)0()0(  xx



. Выпол-

няя замену

ux 



, получаем уравнение с разделяющимися переменными

gluu  /



начальным условием

0)0( u

, которое и решается стандартным способом

dtl

glu

)/1(





glu

)/1(







Clgt

glu

ln/2ln 

















 

lgtC

glu

/2exp 





Из начального условия

0)0( u

получаем

1C

, то есть

 

lgt

/2exp1

)(







Вводя обозначение







, и используя тождество

)th())2exp(1/())2exp(1( zzz 

формулы для скорости и координаты записываем в виде

 

   





/th/

/2exp1

/)( tl

ltu 







   

)/ch(ln/th)/()(



tldttltx





Пример. Одномерное движение частицы в потенциальном поле.

Требуется решить уравнение

)(xfxm 



, где внешняя сила

)()( xUxf





. Умножение

обеих частей данного уравнения на скорость и интегрирование подстановкой дает кон-

станту, называемую интегралом энергии

0)( 



 xxUxxm



EdxxUxdxmdtxxUxxm 











)())((



ExUxm  )(2/



Решив интеграл энергии относительно производной, получаем уравнение с разделяющи-

мися переменными

mxUEx /2))(( 



. В качестве конкретного примера рассмотрим

случай гармонического осциллятора

2/)(

xmxU





Exmxm  2/2/

222





. Обозначив

/2 amE





, получаем

22222

axx







xax 













Результат интегрирования последнего уравнения можно записать одним из следующих

способов



 tax )/arcsin(

)sin()(



 tatx

или



 tax )/arccos(

)cos()(



 tatx

Входящие в конечные формулы константы



определяются по начальным условиям.

Например, при

0)0(,)0(  xax



получаем

)cos()( tatx





, а при

Vxx  )0(,0)0(



, -

 

)sin(/)( tVtx





Квадратичную по скорости силу сопротивления можно записать в виде

lxmf





, где

- постоянная

размерности длины,

- масса частицы, или в виде

/Vxmgf





, где

- скорость равномерного па-

дения частицы,

- ускорение свободного падения.

Начальные сведения о дифференциальных уравнениях

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Пример. Найти общее решение уравнений:

а)





xyyyx

, b)

323

yyxyx 



, c)

0)(













yyxyx

, d)

)cos(

xxyyx 



, e)

yyyyy











)(

, f)

0),exp()22()4(









xxyxyxxyx

a) Замена Бернулли

)()(

xyxz





)()()(

xyxyxz









, сводит исходное уравнение к

линейному

01/ 



xzz

. В то же время, нестандартная замена

)(/)( xyxxu 

)(/))()(()(

xyxyxxyxu







дает

xu 



cxyx  2//

b) Данное уравнение также сводится к линейному заменой Бернулли

)()(

xyxz





. В

то же время, данное уравнение является частным случаем однородного уравнения

)/(/ xyxyy 



. Тогда

xxyxt /)()( 

ttx 



2/)ln( yxxc 

c) Замена

)()( xyxxz





)()()( xyxyxxz











дает уравнение с разделяющимися пере-

менными

xzz /





cxz  )ln(/1

)))(ln(/(1 cxxy 



))ln(ln( ccxy 

. Кроме

того, решением исходного уравнения является любая константа.

d) Данное уравнение является линейным. Однако замена

xxyxt /)()( 

позволяет ре-

шить его быстрее

)cos(

xxtx 





 dxxxxy )cos(/

e) Исходное уравнение имеет тривиальное решение

Cy 

, включающее и случай

0y

. Полагая

0y

и замечая, что

 

/))((/ yyyyyy











, получаем уравнение

 

yyy







. Отсюда следует уравнение с разделяющимися переменными

cyyy 



cyy



 )(

. При

0c

получаем

/1 cxy 

, а при

0c

111

cxdy

cyyc





















, или





f) Уравнение может быть переписано в виде

)exp())2((

xyxxyx 







, откуда по-

лучается линейное уравнение первого порядка

)exp()2( cxyxxyx 



, кото-

рое можно еще более упростить заменой

)(

xzyx 

. Тогда

)exp( cxzz 



zzz 

0



)exp( xCz



)exp()( xxFz



)exp()exp()( cxxxF 



)exp(2/)2exp()(

xcxxF 

2/)exp( cxz



. Окончательно получаем

/2/)exp(/)exp( xcxxxxCy 

Иногда при нахождении решения в ходе вычислений можно непосредственно использо-

вать начальные условия.

Пример. Решить уравнение

)1()(









yyyyy

с начальными условиями

3)0(,1)0( 



 yy

Используя тождество

)/(1)/( yyyyy







, исходное уравнение можно переписать в виде

0)/3/(





 yyy

. Интегрируя это уравнение с учетом начальных условий, получаем

уравнение

3/2/3/





 yyy

. Это уравнение с разделяющимися переменными

3/)/2(1

yyy 





, общее решение которого имеет вид

3/)ln(3

yyCx 

. Из началь-

ного условия получаем

3/1C

, то есть искомое решение

3/)ln(3/13

yyx 

Замена Бернулли

)()( xyxz

n



сводит уравнения вида

)()(







yxbyxay

к линейным.

Начальные сведения о дифференциальных уравнениях

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Линейные дифференциальные уравнения с постоянными

коэффициентами

Основные определения и общее решение однородных уравнений

Линейными дифференциальными уравнениями с постоянными коэффициентами называ-

ются дифференциальные уравнения вида

)()()()()(

)1(

)(

tftxctxctxctx









где

числовые константы, называемые коэффициентами уравнения (здесь и далее в этом

разделе искомая функция обозначается

)(tx

, а для обозначения производных низших по-

рядков используются обозначения с точками). В частном случае

0)( tf

, уравнение назы-

вается однородным, а в общем случае, - неоднородным.

С точки зрения общей геометрической теории, данное уравнение описывает эволюцию

динамической системы, состояние которой задается вектором в

n

мерном фазовом про-

странстве

))(),(,),(),(()(

)2()1(

txtxtxtxtx











, то есть для задания начального условия для

рассматриваемого уравнения необходимо задать в начальный момент

значение функ-

ции и всех ее производных вплоть до порядка

1n

включительно.

Для записи линейного дифференциального уравнения с постоянными коэффициентами

удобно использовать его символическую запись при помощи дифференциального опера-

тора. Обозначая символом (оператором)

операцию дифференцирования, производную

первого порядка можно записать в виде

)()( txtDx





, а производные высших порядков

можно представить с помощью степени оператора дифференцирования

, то есть

)()(

)(

txtDx



. В этих обозначениях исходное дифференциальное уравнение можно запи-

сать кратко с помощью многочлена от оператора дифференцирования, - дифференциаль-

ного оператора с постоянными коэффициентами порядка

)()()( tftxDP



где

)( cDcDcDDP







В силу линейности операции дифференцирования

)())(( tDxсtxсD 

дифференциальные

операторы с постоянными коэффициентами являются линейными операторами, и пере-

множаются как обычные многочлены, то есть алгебра дифференциальных операторов с

постоянными коэффициентами эквивалентна алгебре обычных многочленов от числовой

переменной. Последнее утверждение принципиально важно, так как позволяет перенести

на дифференциальные операторы с постоянными коэффициентами многие результаты ал-

гебры многочленов, в том числе и основную теорему алгебры. Последний результат фор-

мулируется в виде следующего утверждения: дифференциальный оператор с постоянны-

ми коэффициентами порядка

может быть разложен в произведение

линейных со-

множителей

nkDDDcDcDcD









,)()()(

2101





где числа



являются корнями так называемого характеристического уравнения





czczcz



, определяемого коэффициентами исходного дифференциаль-

ным оператором.

Важность последнего утверждения состоит в том, что знание корней характеристического

уравнения позволяет без вычислений выписать общее решение однородного линейного

дифференциального уравнения с постоянными коэффициентами согласно следующему

Начальные сведения о дифференциальных уравнениях

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

правилу: общее решение однородного уравнения является линейной комбинацией

базис-

ных функций





llo

tctx

)()(



, при этом сомножителю

D )(





в разложении опера-

тора в произведение линейных сомножителей соответствует серия

базисных функ-

ций

))exp(,),exp(),exp(),(exp(

ttttttt

jjj









Приведенное правило получается на основе решения простейшего линейного дифферен-

циального уравнения первого порядка

)exp()()( tctxD 



, которое является неодно-

родным уравнением.

Общее решение простейшего уравнения дается формулой

)exp()(

tctx





, а частное ре-

шение

)exp()()( ttFtx





вычисляется методом вариации постоянной

))exp(()( tctF

























,),)exp((

)(



















.),exp(

,),exp(

)(





ttc

В последней формуле введено обозначение







. Случай





называют резонанс-

ным, а случай





- нерезонансным. Полученные решения приведены в таблице 1.

Таблица 1. Общие решения простейшего уравнения с постоянными коэффициентами

Нерезонансный случай

Резонансный случай

Уравнение

)exp()()( tctxD 



)exp()()( tctxD 



Решение

)exp())/(()exp(

tctс





)exp()exp()(

ttctctx





Покажем, как при помощи решений простейших уравнений и замены функций получают-

ся правила выписывания базисных функций для однородных уравнений второго порядка.

Когда корни характеристического уравнения различны

0)())((

 txDD



, получаем

)exp()exp()(

),exp()()(

),exp()(

,0)()(

),()()(

2211

tctctx

tctxD

tctz

tzD

tztxD



























то есть решение является линейной комбинацией базисных функций

))exp(),(exp(



Когда корни характеристического уравнения совпадают

0)()(

 txD



, имеем

)exp()exp()(

),exp()()(

),exp()(

,0)()(

),()()(

1211

ttctctx

tctxD

tctz

tzD

tztxD



























то есть решение является линейной комбинацией базисных функций

))exp(),(exp(

ttt





Общий случай однородного уравнения отличается от случая уравнения второго порядка

только большим числом промежуточных замен функций в ходе вычислений.

В заключении сделаем замечание о способах записи базисных функций и решения одно-

родного уравнения для случая когда его коэффициенты являются вещественными. В этом

случае коэффициенты характеристического уравнения являются вещественными, и его

корни можно сгруппировать в комплексно сопряженные пары

),(



ii 

Базисные функции, связанные с комплексно сопряженными корнями также можно сгруп-

пировать в комплексно сопряженные пары

)))exp((),)exp((( tittit





, а посколь-

Начальные сведения о дифференциальных уравнениях

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

ку искомое решение является вещественной функцией, вклад в него от комплексно со-

пряженной пары базисных функций должен быть вещественным, то есть представляться

суммой комплексно сопряженных слагаемых

скtitС

.))exp(( 



Преобразование комплексной экспоненты при помощи формулы Эйлера

))sin())(cos(exp()exp()exp())exp(( titttitti





и запись комплексной констан-

ты в виде

2/2/

iccC 

, позволяет представить вклад в общее решение от комплексно

сопряженной пары базисных функций через тригонометрические функции

)sin()exp()cos()exp(.))exp((

tttctttcскtitС

kkk





Таким образом, для записи решения однородного уравнения вместо комплексно сопря-

женной пары базисных функций

)))exp((),)exp((( tittit





можно использовать

пару вещественных базисных функций

))sin()exp(),cos()exp(( tttttt





. При этом

вопрос об использовании комплексно сопряженных или вещественных базисных функций

решается исключительно соображениями удобства их использования в конкретной задаче.

Пример. Свободные колебания затухающего гармонического осциллятора.

Требуется найти вещественные решения однородного уравнения

0)()(2)(

 txtxtx





Характеристическое уравнение имеет вид





, а его корни зависят от соот-

ношения между параметрами





























Решения выписываются по корням характеристического уравнения, при этом для записи

решения в случае комплексно сопряженных корней используем вещественный базис



































.),exp()exp(

,),exp()(

,),sincos)(exp(

)(

021







tctc

ttcc

tctct

Решение неоднородных уравнений с квазимногочленом

Комплексная функция вещественной переменной называется квазимногочленом, если она

может быть представлена в виде суммы



 )exp()()( ttptf



, где

)(tp

- многочлен с

комплексными коэффициентами, а



- комплексные константы.

В силу принципа супер-

позиции следует, что решение неоднородного уравнения



 )exp()()()( ttptxDP



представляется в виде суммы решений уравнений вида

)exp()()()( ttptxDP





. То есть

для нахождения решений уравнений с правой частью квазимногочленом достаточно уметь

вычислять частное решение для уравнений с правой частью вида

)exp()( ttp





Как будет видно из приводимых ниже примеров, квазимногочлены являются достаточно широким классом

функций. Кроме того, разложение функции в интеграл Фурье











dtiftf )exp()(

)(

можно рассмат-

ривать как обобщение понятия квазимногочлена на случай «непрерывной суммы» однотипных слагаемых.

Начальные сведения о дифференциальных уравнениях

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Используя описанное выше разложение дифференциального оператора с постоянными

коэффициентами в произведение линейных сомножителей, нетрудно догадаться, что вы-

числение решения неоднородного уравнения, также как и вычисление решений однород-

ного уравнения может быть сведено к последовательности решений простейших уравне-

ний первого порядка. Получаемый таким образом результат можно сформулировать в ви-

де следующих правил подбора формы решения по правой части уравнения:

 Если в уравнении

)exp()()()( ttptxDP





константа



не является корнем харак-

теристического уравнения (резонанса нет), частное решение неоднородного урав-

нения имеет вид

)exp()()(

tctctctctx









 Если в уравнении

)exp()()()( ttptxDP





константа



является корнем характе-

ристического уравнения кратности

(резонанс порядка

), частное решение неод-

нородного уравнения имеет вид

)exp()()(

tctctctcttx









Входящие в формулы решений неизвестные коэффициенты определяются из системы

уравнений, получаемой из условия равенства многочленов в левой и правой части исход-

ного уравнения.

Пример. Колебания незатухающего осциллятора под действием гармонической силы.

Требуется найти действительное частное решение неоднородного уравнения

)cos()()(

tftxtx







, правая часть которого

2/))exp()(exp()cos( titit





является

суммой квазимногочленов нулевого порядка. Решение можно получить, используя прин-

цип суперпозиции. Однако проще воспользоваться линейностью операции выделения

действительной части комплексного числа

)Re()Re()Re(

2121

zzzz 

, решить вспомога-

тельное уравнение

)exp()()(

tiftztz







для комплексной функции

)(tz

, и найти ис-

комое решение путем выделения ее действительной части

)(Re)( tztx 

. Решение одно-

родного уравнения записываем через комплексно сопряженные базисные функции

..)exp()( скtictz





. При условии





резонанса нет, а при





имеет место резо-

нанс первого порядка. В нерезонансном случае решение ищется в виде

)exp()( tiatz





Подстановка этого решение в уравнение для

)(tz

дает:

)exp()exp()(

tiftia











)exp(

)(









tif

)cos(

)(









В резонансном случае решение ищется в виде

)exp()(

titatz





. Его вторая производная

)exp(2)exp()(

000

tiaititatz







. Подстановка решения и производной в исходное

уравнение для функции

)(tz

дает

)exp()exp(2

000

tiftiai







a 

)exp(

)(





)sin(

)(





Преимущество приведенного способа решения заключается в том, что при помощи выде-

ления мнимой части полученного комплексного решения

)(tz

сразу получается и решение

уравнения с синусоидальным воздействием

)sin()()(

tftyty

























.),cos(

,),sin(

)(









Начальные сведения о дифференциальных уравнениях

Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева

Решение неоднородных уравнений вариацией постоянных

Когда правая часть неоднородного уравнения не является квазимногочленом, его частное

решение вычисляется методом вариации постоянных, который обобщает метод вариации

постоянной для уравнения первого порядка. Это метод реализуется следующими шагами:

1. Выписывают общее решение однородного уравнения

)()()()(

2211

tctctctx

nno



 

2. Исходное неоднородное уравнение записывается в виде системы

уравнений пер-

вого порядка















),()(

tftx

txtx







выписывается решение однородной системы













































),()()()(

,0)(

),()(

)1()1(

)1(

111

22111

2211

tctctctx

txtx

nno















замена в котором констант

на функции и дает искомую форму частного решения

неоднородной системы































).()()()()()()(

),()()()()()()(

)1()1(

)1(

111

22111

2211

ttfttfttftx









3. Подстановка выписанного решения в неоднородную систему дает систему линей-

ных уравнений для производных

)(tf



искомых функций

















































),()()()()()()(

,0)()()()()()(

)1()1(

)1(

2211

tfttfttfttf

ttfttfttf









после решения которой функции

)(tf

находятся интегрированием.

Пример. Незатухающий гармонический осциллятор под воздействием произвольной силы.

Требуется решить неоднородное уравнение

)()()(

tftxtx 





. Решение однородного

уравнения записываем в виде линейной комбинации вещественных базисных функций

)sin()cos()(

0201

tctctx





, а исходное уравнение, - в виде системы уравнений первого

порядка











).()()(

),()(

tftxtp

tptx





С помощью первого уравнения системы

)()( tptx 



выписываем решение однородной сис-

темы, и, варьируя постоянные, получаем формулу для частного решения