Алексеев Д.В. Конспекты по общему курсу математики
Подождите немного. Документ загружается.


Векторная алгебра и аналитическая геометрия 19
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
).()()(
,)(
));(;1()()),(;()(),()()(
aftafty
tatx
afaVafaaRaVtaRtR
Поскольку график функции – это множество точек на плоскости, координаты которых за-
даны формулой
))(;( xfx
, с функцией
)(xfy
можно связать векторную функцию на
плоскости
))(;()( xfxxRx
. Ее координатными функциями является пара функций
)(, xfx
. Нетрудно увидеть, что пара функций,
)(,1 xf
, входящая в формулу координат
вектора параллельного касательной, является производными этих координатных функций.
На основании изложенного приходим к следующему принципиальному выводу. Операция
дифференцирования числовой функции может быть определена чисто геометрически, как
сопоставление каждой точке графика функции
))(;( xfx
вектора
))(;1( xf
, параллельного
касательной к графику в этой точке. При этом координатные функции касательного век-
тора получаются дифференцированием координатных функций графика при помощи
обычных правил дифференцирования.
Простейшими примерами годографов векторных функций являются линии на плоскости,
задаваемые векторными функциями вида
))();(()( tytxtRt
.
Операция дифференцирования векторной функции на плоскости определяется по анало-
гии с описанной в предыдущем разделе геометрической процедурой дифференцирования
обычной числовой функции. Продифференцировать векторную функцию – это сопоста-
вить каждой точке из ее области значений (точке годографа) касательный вектор к годо-
графу.
))();(()()()( tytxtRtVtR
.
Координатные функции касательного вектора вычисляются при помощи дифференциро-
вания координатных функций исходной векторной функции:
Касательный вектор к годографу будет определен только тогда, когда определены все
производные координатных функций. Если касательный вектор определен в любой точке
годографа, определяемая годографом линия называется гладкой, а соответствующая ей
векторная функция – дифференцируемой. Если годограф является непрерывной линией,
составленной из нескольких гладких кусков, векторная функция называется кусочно-
дифференцируемой, а ее годограф – кусочно-гладкой линией.
Дифференцирование векторной функции в пространстве произвольной размерности также
проводится путем определения касательного вектора, который вычисляется дифференци-
рованием всех координатных функций
))();();();(()(
321
tRtRtRtRtV
n
.
Заметим, что касательный вектор к годографу часто называют вектором скорости. Это
связано с тем, что понятие векторной функции широко используется в задачах механики
точки, в которых годограф отождествляется с траекторией, а также с тем, что аналогия с
механикой точки является весьма плодотворной для самой теории векторных функций.
Поставим вопрос: всегда, ли две различные векторные функции имеют различные годо-
графы?
Ответ на этот вопрос отрицательный. Можно привести бесконечное множество различных
векторных функций, имеющих одинаковый годограф. Для примера, воспользуемся на-

Векторная алгебра и аналитическая геометрия 20
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
глядным представлением из механики точки. Пусть точка движется по прямой линии. Вы-
бирая подходящую систему координат, совместим эту прямую с осью абсцисс. Тогда век-
торная функция будет задаваться единственной координатной функцией:
itutR
)()(
. Яс-
но, что в последней формуле функция
)(tu
является абсолютно произвольной. То есть од-
ному годографу – оси абсцисс соответствует бесконечное множество векторных функций.
Для уменьшения этого произвола в теории векторных функций вводится понятие ориен-
тации линии. На языке механической аналогии понятие ориентации линии означает, что
точке запрещено менять направление движения. То есть ориентированная линия это тра-
ектория точки с указанием направления движения.
Рассмотрим следующий вопрос: когда две различные векторные функции описывают од-
ну ориентированную линию? Для этого рассмотрим две векторные функции
)(),( sStR
,
получаемые одна из другой при помощи замены переменной:
)(st
. Для совпадения
годографов функций
)(),( sStR
с учетом ориентации необходимо, чтобы при изменении
переменной
s
значения функции
)(st
пробегали область определения функции
))(( tRD
, не изменяя направления движения. То есть приращение функции
dssdt )(
должно иметь тот же знак, что и приращение переменной
ds
. Для этого производная
)(s
должна быть положительной.
Интегрировать векторную функцию можно различными способами. Первый способ ин-
тегрирования векторной функции дает вектор, и связан с вычислением прямолинейного
перемещения из одной очки годографа другую. Второй способ интегрирования дает ска-
ляр, и связан с вычислением длины криволинейного отрезка годографа. Оба способа ин-
тегрирования находят разнообразное применение в прикладных задачах. Поскольку годо-
граф дифференцируемой векторной функции является гладкой кривой, ниже будем ото-
ждествлять понятия кривой и годографа
Вычислить перемещение – это найти вектор, соединяющий начальную и конечную точки
на линии. Пусть параметр векторной функции
)(tRt
изменяется в интервале
bta
.
Разобьем этот интервал на большое число
N
равных частей
NkNabdtkdtat
k
;2;1;0,/)(,
,
вычислим значение функции и касательный вектор в каждой точке деления и составим
интегральную сумму
N
k
k
dttV
0
)(
.
Каждое слагаемое в интегральной сумме является малым перемещением вдоль касатель-
ного вектора, вычисленного в точке годографа
)(
k
tR
. С точностью до поправок, являю-
щихся бесконечно малыми второго порядка по приращению
dt
, это перемещение равно
вектору, соединяющему две соседних точки линии
)()()(
1 kkk
tRtRdttV
.
Используя стандартное правило перехода к пределу в интегральной сумме, получаем
формулу интегрирования векторной функции
)()())()((lim)(lim)(
0
1
0
aRbRtRtRdttVdttV
N
k
kk
N
N
k
k
N
b
a

Векторная алгебра и аналитическая геометрия 21
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Полученная формула интегрирования векторной функции является аналогом формулы
Ньютона-Лейбница, которую можно записать в виде:
b
a
dttVaRbRtVtR )()()()()(
.
Аналогия с формулой Ньютона–Лейбница особенно ясно видно в координатной записи
вектора перемещения. Например, для линии на плоскости координатная запись имеет вид:
))()()(;)()()(()()(
b
a
b
a
dttyaybydttxaxbxaRbR
.
Переход к случаю линий в пространстве произвольной размерности будет отличаться
только числом координатных функций.
Вычисление длины гладкой кривой связано с процедурой интегрирования модуля скоро-
сти. Отличие этой процедуре интегрирования от описанной выше процедуры вычисления
перемещения состоит в суммировании путей – длин перемещений, а не векторов. Для вы-
числения длины кривой выполним ее разбиение, описанное в предыдущем разделе, и со-
ставим интегральную сумму
N
k
k
dttV
0
|)(|
.
Каждое слагаемое выписанной интегральной суммы является длиной малого перемещения
вдоль касательного вектора. Входящая в это слагаемое длина вектора скорости вычисля-
ется по стандартной формуле. Например, для трехмерного вектора
)()()(|)(|
222
tVtVtVtV
zyx
.
Формула для длины криволинейного отрезка получается при помощи стандартного пере-
хода к пределу в интегральной сумме
b
a
N
k
k
N
ba
dttVdttVL |)(||)(|lim
0
.
Выражение, находящееся под интегралом, называется дифференциалом длины дуги и
полностью определяется вектором скорости
dttVdl |)(|
.
При помощи дифференциала длины дуги формула для длины криволинейного отрезка за-
писывается в виде
b
a
ba
dlL
.
Из этой формулы можно сделать следующий вывод. Если рассматривать длину кривой как
параметр векторной функции, то формула для длины кривой будет иметь простейший вид.
Это обусловлено тем, что входящая в нее длина вектора скорости равна единице. Этот
вектор скорости называется единичным касательным вектором. Формулу для единичного
касательного вектора получается при помощи правила дифференцирования сложной
функции и определения произвольного касательного вектора
|)(|/)()//()()( tVtVdtdltV
dl
dt
dt
Rd
dl
Rd
le
.
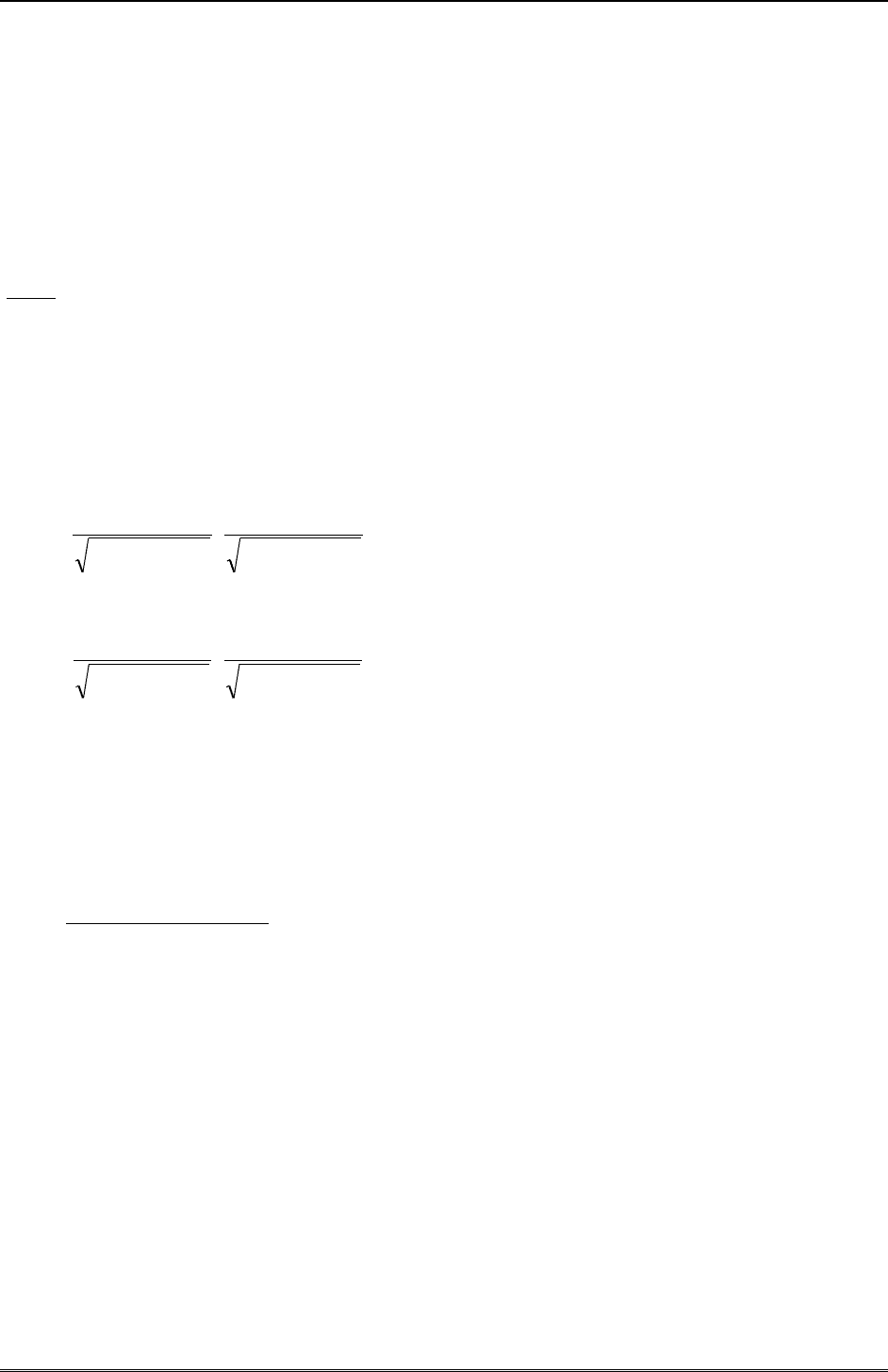
Векторная алгебра и аналитическая геометрия 22
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Параметризация векторной функции при помощи параметра длины кривой называется ес-
тественной параметризацией, а сама длина – естественным параметром кривой.
Понятие естественной параметризации кривой и единичного касательного вектора нахо-
дят применение при определении понятия кривизны плоских кривых. В механике точки
понятие кривизны линии связано с понятием центростремительного ускорения, возни-
кающего при движении по криволинейной траектории с постоянной скоростью
ConstV ||
.
Кривизна плоской кривой
)(tk
определяется при помощи уравнения
)()(
)(
tntk
dl
ted
,
где
)(tn
- единичная нормаль к кривой определяемая согласно следующим условиям:
0))(),(( tnte
;
вектор
)(tn
получается поворотом вектора
)(te
против хода часовой стрелки.
Так как единичный касательный вектор к плоской кривой имеет вид
)
)()(
)(
;
)()(
)(
()(
2222
tVtV
tV
tVtV
tV
te
yx
y
yx
x
,
то единичная нормаль записывается в виде
)
)()(
)(
;
)()(
)(
()(
2222
tVtV
tV
tVtV
tV
tn
yx
x
yx
y
.
Для записи формулы кривизны введем следующие обозначения для вторых производных
координатных функций:
)()();()( tatytatx
yx
.
Тогда непосредственно из уравнения, определяющего кривизну, при помощи правила
дифференцирования сложной функции получаем формулу
2/322
))()((
)()()()(
)(
tVtV
tatVtatV
tk
yx
xyyx
,
выражающую кривизну через производные координатных функций.
Для уяснения понятия кривизны, рассмотрим векторную функцию, описывающую равно-
мерное движение по окружности в естественной параметризации:
ALLlALlAlR
2),/2sin();/2cos(()(
.
Вычисляя все необходимые производные, получаем, что кривизна при равномерном дви-
жении по окружности является постоянной:
Ak /1
.
То есть при равномерном движении по окружности кривизна является величиной обратно
пропорциональной радиусу окружности.
Альтернативным способом описания линий на плоскости является их рассмотрение как
годографов векторных функций
)}();({)( tytxtR
.

Векторная алгебра и аналитическая геометрия 23
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
Эллипс, с центром симметрии в точке
);(:
00
yxС
, полуосями
a
,
b
и осями симметрии,
параллельными координатным осям, задается векторной функцией
)}sin();cos({)(
00
tbytaxtR
.
Чтобы убедиться в этом, достаточно исключить параметр при помощи основного триго-
нометрического тождества
.1/)(/)(
),(sin/)(
),(cos/)(
),sin(
),cos(
22
0
22
0
222
0
222
0
0
0
byyaxx
tbyy
taxx
tbyy
taxx
В отличие от эллипса гипербола состоит из двух ветвей. Поэтому для ее задания необхо-
димо использовать две векторные функции, по одной функции для каждой ветви. Напри-
мер, гипербола с центром симметрии в начале координат, действительной полуосью
a
и
мнимой полуосью
b
, задается векторными функциями
)}sinh();cosh({)(
1
tbtatR
,
)}s inh();cosh({)(
2
tbtatR
.
Первая функция описывает левую ветвь гиперболы, расположенную в правой полуплос-
кости, а вторая – ветвь в левой полуплоскости. Каноническое уравнение гиперболы полу-
чается при помощи исключения параметра с помощью основного тождества для гипербо-
лических функций
.1//
),(sinh/
),(cosh/
),sinh(
),cosh(
2222
222
222
byax
tby
tax
tby
tax
Простейшая парабола
2
xy
задается векторной функцией
};{)(
2
tttR
.
Если векторная функция
)}();({)( tytxtR
определяется дифференцируемыми координат-
ными функциями, ее годограф определяет гладкую кривую. В любой точке гладкой кри-
вой касательный вектор
)}();({)( tytxtV
определен однозначно. Примерами гладких
кривых на плоскости являются все рассмотренные выше линии второго порядка.
Если в некоторых точках линии касательный вектор не определяется однозначно, то такая
линия называется кусочно-гладкой

Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
1
Начальные сведения о теории вероятностей
Пространства событий и вероятности
Теория вероятностей имеет дело с количественным описанием понятия случайности, ос-
нованным на представлении о случайном эксперименте. Случайный эксперимент это про-
цесс, точный исход которого нельзя предсказать, однако можно заранее перечислить все
его возможные исходы. Множество всех альтернативных исходов случайного экспери-
мента, которые нельзя представить в виде совокупности более простых исходов того же
случайного эксперимента, называется пространством элементарных исходов или про-
странством элементарных событий, конкретный вид которого определяется рассматри-
ваемым случайным экспериментом. Пространство элементарных событий является пер-
вым базовым понятием теории вероятностей. Нельзя решить вероятностную задачу без
ясного представления о пространстве элементарных событий.
При формулировке различных утверждений в вероятностных задачах, наряду с элемен-
тарными событиями используются также составные события. Составные события строят-
ся путем объединения нескольких элементарных событий в единый объект по некоторому
общему для элементарных событий условию. Используя теоретико-множественную сим-
волику для операций объединения и пересечения множеств, можно построить формаль-
ную алгебру событий. Однако на начальном этапе изучения проще и полезнее отказаться
от формальной алгебры и использовать при работе с событиями словесные формулировки.
Вторым основным понятием теории вероятностей являются функции, определяемые на
пространстве событий. Функции на пространстве событий строятся стандартным образом:
функция, это однозначное соответствие между элементами пространства событий, - обла-
стью определения функции, и множеством некоторых других объектов, - областью значе-
ний функции. Природа области значений рассматриваемых на пространстве событий
функций может быть достаточно разнообразной, - векторы, матрицы, действительные и
комплексные числа, и т.п. Среди функций на пространстве событий наиболее часто встре-
чаются вещественные числовые функции, областью значений которых являются множест-
ва вещественных чисел, называемые случайными величинами.
Среди всех случайных величин выделяют функции, принимающие значения в интервале
[0;1], которые характеризуют относительную частоту появления конкретного события при
достаточно длительном повторении рассматриваемого случайного эксперимента. Эти
функции называются вероятностями событий, которые и являются третьим основным
понятием теории вероятностей.
Конечные пространства событий
Простейшие примеры пространств событий предоставляют случайные эксперименты с
равновероятными альтернативными исходами, общее число которых конечно: подбрасы-
вание «правильных» монет или игральных костей, вытаскивание карт из «хорошо перета-
сованной» колоды и т. п.
В таких случайных экспериментах вероятности исходов подсчитываются по правилу:
Вероятность события = (Число благоприятных исходов)/(Полное число исходов).
Выписанное правило подсчета вероятностей называется постулатом равной априорной
вероятности. Это название подчеркивает, что равная вероятность альтернативных эле-
ментарных исходов постулируется заранее (априори), на основе некоторых «разумных со-
ображений», которые в реально осуществляемых реализациях рассматриваемых случай-
ных экспериментов могут и не выполняться. Например, колода карт тасуется не достаточ-

Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
2
но тщательно, игральная кость имеет смещенный центр тяжести, и т. п. Разработка коли-
чественных критериев, используемых для обоснования согласия рассматриваемой вероят-
ностной модели, с экспериментальными данными (данными наблюдений) составляет
предмет математической статистики и здесь не рассматривается.
Приведем несколько примеров вычисления вероятностей на основе постулата равной ап-
риорной вероятности.
Случайные совпадения.
Письма разным адресатам случайно размещаются по заранее подготовленным для от-
правки конвертам. Какова вероятность того, что все письма попадут по назначению?
Пространством элементарных являются различные варианты раскладки писем по конвер-
там с соблюдением ограничения: в одном конверте одно письмо. Если всего имеется
n
конвертов, то первое взятое письмо можно поместить в любой из
n
конвертов, второе - в
любой из оставшихся
1n
конвертов, третье - в любой из оставшихся
2n
конвертов, и
так далее. Последнее письмо помещается в единственный оставшийся конверт. Полное
число возможных вариантов раскладки писем равно произведению вариантов раскладки
каждого из писем, то есть
!n
. Событию «все письма попали по назначению» соответствует
единственный благоприятный вариант. Следовательно, искомая вероятность равна
!/1 n
.
Равновесие при бросании монет.
Какова вероятность того, что при бросании четного числа монет число выпавших гер-
бов будет равно половине числа монет?
Поскольку каждая из
n2
монет может упасть на одну из сторон (падение на ребро исклю-
чается из рассмотрения), полное число элементарных событий равно
n2
2
. Число благо-
приятных исходов для события «выпало
n
гербов» подсчитывается следующим образом.
Из
n2
монет
n
штук можно выбрать
!/)!2( nn
способами (размещение
n
писем по
n2
конвертам!). Поскольку порядок выбора монет для подсчета числа гербов не играет роли
(все гербы одинаковы), полученное число необходимо поделить на число различных вари-
антов упорядочения набора выбранных
n
монет. Следовательно, число благоприятных
событий равно
)!!/()!2( nnn
. Тогда искомая вероятность
n
n
n
n
C
nn
n
nP
2
2
2
2
1
2
1
!!
)!2(
)(
.
Когда число монет велико, для вычисления факториалов можно воспользоваться прибли-
женной формулой Стирлинга
nenn
nn
2!
и вычислить искомую вероятность прибли-
женно по формуле:
nnP
/1)(
.
В тех случаях, когда применимость постулата равной априорной вероятности к рассмат-
риваемому случайному эксперименту не может быть обоснована, для вычисления вероят-
ностей событий используется следующее более общее правило:
Вероятность события = Сумма вероятностей благоприятных элементарных событий.
В отличие от правила основанного на постулате равной априорной вероятности, здесь ве-
роятности различных элементарных событий не являются равными, но, по прежнему, яв-
ляются заданными заранее (априори).
Бесконечные дискретные пространства событий
Бесконечные дискретные пространства событий часто возникают при рассмотрении неог-
раниченных последовательностей однотипных случайных экспериментов
Испытания до первого успеха.

Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
3
Пусть случайный эксперимент состоит в бросании монеты до первого выпадения герба.
Требуется описать пространство событий. Обозначим неудачу символом
н
, а успех (вы-
падение герба) символом
у
.Элементами пространства событий являются последователь-
ности вида
нунн
, число элементов которых равно числу подбрасываний. Поскольку
теоретически число подбрасываний монеты не ограничено, число возможных последова-
тельностей бесконечно.
Испытания до повторения двух неудач подряд. Элементами пространства событий явля-
ются последовательности вида
эуннэээ
, где
ээээ
- любая последовательность, не со-
держащая двух неудач подряд.
Для бесконечных дискретных пространств элементарных событий постулат равной апри-
орной вероятности не применим, так как попытка его применения сталкивается со сле-
дующим простым противоречием: когда число равновероятных элементарных исходов
бесконечно вероятность отдельного элементарного исхода должна быть равна нулю. В
этом легко убедиться, рассматривая предельный переход в формуле для вероятности к
бесконечному пространству событий. Поэтому, в случае бесконечного дискретного про-
странства элементарных исходов для подсчета вероятности используется правило:
Вероятность события = Сумма вероятностей благоприятных элементарных событий.
Конкретные примеры вычисления вероятностей событий по этому правилу будут рас-
смотрены ниже при рассмотрении вероятностей последовательностей событий.
Непрерывные пространства событий и геометрические вероятности
Если элементарные исходы образуют непрерывное множество, то есть вблизи некоторого
выбранного элементарного исхода расположено бесконечное число сколько угодно близ-
ких к нему других элементарных исходов, становится бессмысленным говорить о вероят-
ности отдельного элементарного исхода. Вместо этого необходимо новое правило, при
помощи которого можно сравнивать вероятности различных событий, каждое из которых
представлено некоторым непрерывным множеством. Иногда удается наглядно предста-
вить множества элементарных событий в виде некоторых геометрических множеств: от-
резков линий, плоских или пространственных фигур. Тогда отношение вероятностей двух
событий можно подсчитать по правилу:
Отношение вероятностей = Отношение мер геометрических множеств.
Это правило является обобщением постулата равной априорной вероятности на случай
непрерывных пространств событий и может быть применено только тогда, когда все про-
странство элементарных событий может быт представлено в виде геометрического мно-
жества конечного размера. Поскольку описанное правило вычисления вероятностей осно-
вывается на понятии геометрической меры множества (длины, площади или объема), ве-
роятности, рассматриваемые в подобных задачах, называют геометрическими вероятно-
стями. В некотором смысле геометрические вероятности подобны вероятностям на конеч-
ном пространстве элементарных событий, определяемым на основе постулата равной ап-
риорной вероятности.
Приведем несколько примеров вычисления геометрических вероятностей.
Случайное расположение точек.
Внутри квадрата со стороной
2A
с центром в начале координат случайно помещается
точка
M x y:( ; )
. Вычислить вероятность:
)(
222
RyxP
при различных значениях
R
.
Пространство событий является исходным квадратом, а интересующее нас событие - кру-
гом радиуса
R
с центром в начале координат. Различные варианты взаимного расположе-
ния квадрата и круга представлены на рисунке.

Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
4
R>A
2
A<R<A
2
R<A
Когда радиус круга больше диагонали квадрата точка наверняка попадает внутрь круга,
когда радиус меньше стороны квадрата искомая вероятность равна отношению площади
круга к площади квадрата, в промежуточном случае искомая вероятность равно отноше-
нию площади пересечения круга и квадрата к площади квадрата. Ответ:
.2 ,1
;2 )),/arccos(4/)(/(1/
; ,4/
)(
2222
22
222
AR
ARARAARAR
ARAR
RyxP
Случайные хорды.
На окружность заданного радиуса случайно рисуется хорда. Вычислить вероятность
события «длина хорды больше радиуса».
Решение задачи сильно зависит от конкретизации того, что понимается под случайно на-
рисованной хордой. Приведем два варианта решения, оба из которых являются верными.
Вариант 1. Хорда определяется расстоянием
d
ее середины от центра окружности.
Тогда пространством элементарных событий будет исходный круг радиуса
R
, а
искомой вероятности события будут соответствовать точки внутри круга радиуса
R 3 2/
. Тогда искомая вероятность равна отношению площадей
4/3/)2/3()2/3(
22
RRRdP
.
Вариант 2. Хорда определяется случайным центральным углом между ее концами.
Тогда пространство элементарных событий представляется интервалом
0
.
Чтобы хорда была длиннее радиуса, угол должен находиться в интервале
/ 3
. Из отношения углов находим искомую вероятность
3/2/)3/2()3/(
P
.
Если непрерывное пространство событий не может быть представлено в виде конечного
геометрического множества условие равенства вероятностей элементарных исходов не
может быть реализовано. В этом смысле ситуация напоминает ту, которая имеет место для
бесконечного дискретного пространства событий, то есть в рассмотрение необходимо
вводить функцию, описывающую вероятности элементарных исходов. Например, пусть
пространство событий отождествляется с числовой прямой, и пусть на числовой прямой
задана положительная функция
)(xp
, удовлетворяющая условию нормировки
1)(
dxxp
Тогда определенный интеграл
b
a
dxxp )(
, можно трактовать как вероятность реализации
группы элементарных событий из интервала
);( ba
, а дифференциал
dxxp )(
- как вероят-
ность реализации элементарных событий из бесконечно малого интервала
);( dxxx
.
Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
5
Описанная конструкция может быть обобщена и на более сложные случаи, когда про-
странство событий может быть отождествлено с плоскостью, трехмерным пространством
и даже бесконечномерным пространством (примеры таких построений будут приведены в
главе посвященной случайным величинам). Однако в некоторых случаях решения удается
получить из рассмотрения геометрических вероятностей, как в следующем примере.
Квадратное уравнение со случайными коэффициентами.
Найти вероятность того, что квадратное уравнение
x px q
2
2 0
имеет веществен-
ные корни; положительные корни.
Пространство событий - точки на координатной плоскости с координатами
( ; )p q
. Оно не
является ограниченным геометрическим множеством. Для сведения задачи к схеме гео-
метрической вероятности рассмотрим ее решение на некоторой части плоскости конечно-
го размера, а затем воспользуемся процедурой предельного перехода к бесконечной плос-
кости. Подобно задаче о случайных хордах, данная задача также имеет несколько пра-
вильных решений.
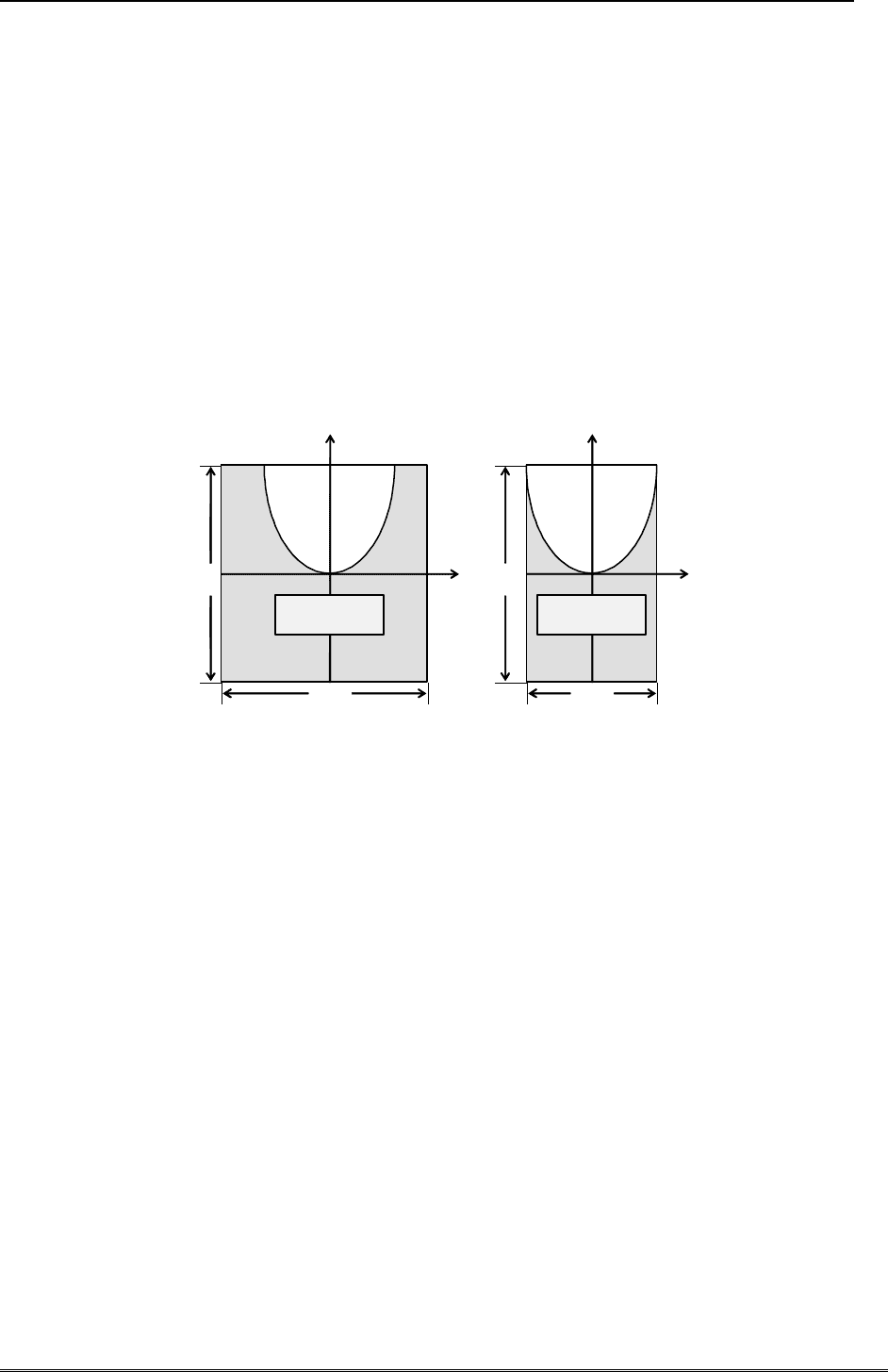
p
q
2L
p q
2
0
2L
p
q
2L
p q
2
0
2L
2
Вариант 1. Вычислим требуемые вероятности на квадрате со стороной
2L
с цен-
тром в начале координат. Событию «корни вещественные» соответствуют точки с
координатами, удовлетворяющими условию
p q
2
0
. Событию «корни положи-
тельные» соответствуют подмножество точек предыдущего события, удовлетво-
ряющие условиям
p q 0 0;
. Находим требуемые отношения площадей непо-
средственно из рисунка:
2/122/12
)6/1(4/1)0;0;0( ;)3/1(1)0(
LqpqpPLqpP
.
В пределе бесконечной плоскости
L
вероятность события «корни веществен-
ные» стремится к единице, а вероятность события «корни положительные - к 1/4.
Вариант 2. Вычислим требуемые вероятности на прямоугольнике со сторонами
2L
и
2
2
L
. В этом случае определяющие требуемые вероятности отношения площадей
оказываются не зависящими от масштаба исходного прямоугольника:
12/1)0;0;0( ;3/2)0(
22
qpqpPqpP
.
Формальная алгебра событий и вычисление вероятностей
Описанные выше на конкретных примерах правила вычисления вероятностей могут быть
формализованы при помощи стандартных операций над множествами. Обозначим про-
странство элементарных событий символом
, а составляющие его элементарные собы-
тия символами
i
для дискретных пространств и символами
( )
для непрерывных про-
странств.
Составные события образуются путем объединения различных элементарных событий по
некоторому общему признаку:
