Алексеев Д.В. Конспекты по общему курсу математики
Подождите немного. Документ загружается.


Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
6
BAi
i
BA
)( ;
.
Для записи операции объединения дискретных событий можно также использовать знак
операции сложения, а для объединения непрерывных событий знак операции интегриро-
вания:
B
Ai
i
dBA
)( ;
.
В частности, все пространство элементарных событий является объединением образую-
щих его элементарных событий:
)( ;
i
i
, или
d
i
i
)( ;
.
Суммой двух составных событий называется множество элементарных событий, входя-
щих в события-слагаемые. При этом каждое из составляющих сумму элементарных собы-
тий входит в сумму только один раз. Сумма событий обозначается
BA
или
A B
.
Формулировка события-суммы читается с использованием союза «или»:
«Произошло А или В».
Множество элементарных событий, входящих одновременно в события А и В называется
произведением событий и обозначается символом пересечения множеств
BA
или при
помощи знака операции умножения
A B
.
Формулировка события-произведения читается с использованием союза «и»:
«Произошло А и В».
Если события-сомножители не содержат общих элементарных событий, то их произведе-
ние является невозможным событием, обозначаемым символом пустого множества
.
Такие события называются несовместными или альтернативными. В частности, любая па-
ра элементарных событий является альтернативной:
,=)()( =)()( ;, ji
jiji
,
так как при реализации случайного эксперимента одновременное появление различных
элементарных исходов невозможно.
Каждому элементарному событию сопоставляется вероятность
p p( ); ( ) 0 1
.
Невозможному событию сопоставляется нулевая вероятность
p( ) 0
.
Вероятность составного события вычисляется как сумма вероятностей составляющих его
элементарных событий:
p A p p B p d
i
i A
B
( ) ( ); ( ) ( ( ))
.
Согласно этому правилу вероятность суммы составных событий вычисляется по формуле:
p A B p A p B p A B( ) ( ) ( ) ( )
.
Смысл формулы для вероятности суммы событий следующий. Вероятность
p A B( )
складывается из вероятностей элементарных событий, входящих в А или В. При этом ка-
ждое элементарное событие должно содержаться в этой сумме только один раз. Так как
сумма вероятностей
p A p B( ) ( )
дважды содержит вероятности элементарных событий
входящих в
A B
, для устранения этого лишнего суммирования вероятностей элементар-
ных событий и проводится вычитание вероятности
)( BAp
.

Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
7
Следствием формулы для вероятности суммы событий является условие нормировки ве-
роятностей на единицу:
p p p p d
i
i
( ) ( ) ; ( ) ( ( ))
1 1
.
Смысл условия нормировки состоит в том, что при реализации случайного эксперимента
одно из элементарных событий обязательно произойдет.
Последовательности событий
Во многих моделях случайных экспериментов приходится иметь дело с событиями, про-
исходящими в определенной последовательности. Например, легко представить реализа-
цию последовательности случайных событий состоящую из результатов подбрасывания
монеты некоторое заданное число раз, или последовательность телеграфного кода, иска-
женную влиянием помех. Общей чертой для всех последовательностей событий является
то, что, работая с последовательностью, мы имеем дело с совместными событиями, одно
из которых не исключает другое. На языке формальной алгебры событий это записывается
в виде следующего условия совместности событий рассматриваемой последовательности:
A A A
N1 2
.
Основная задача при работе с последовательностями событий заключается в вычислении
вероятностей
p A A A
N
( )
1 2
для событий-произведений.
Условная вероятность и статистическая независимость
События, формирующие последовательность, могут быть зависимыми или независимыми.
Зависимость событий в последовательности означает, что некоторые из событий последо-
вательности могут служить причиной появления следующих за ними событий, или влиять
каким-то иным образом на последующие события последовательности. Для последова-
тельности зависимых событий реализация конкретного события-причины приводит к из-
менению протекания случайного эксперимента, что сказывается на вероятности события-
следствия. Для независимых событий напротив, события не влияют друг на друга, и на
вероятности отдельных событий последовательности.
Количественно зависимость событий описывается при помощи условной вероятности.
Понятие условной вероятности опирается на предполагаемую последовательность собы-
тий в паре. Пусть из некоторых соображений известна вероятность совместного события
p A B( )
и вероятность события-причины
p B( )
. Тогда условная вероятность появления
события
A
по причине реализации события
B
вычисляется по формуле:
p A B p A B p B( | ) ( ) / ( )
.
В этой формуле принципиально важно, что причина, - событие
B
, обязательно предшест-
вует следствию, - событию
A
. Поскольку в общем случае
p A B p B A( | ) ( | )
следует четко
различать эти условные вероятности, и читать формулу определения условной вероятно-
сти четко, подчеркивая последовательность событий:
«
p A B( | )
- вероятность реализации
A
при условии что
B
произошло».
Когда события являются независимыми, вероятность последующего события не зависит
от реализации предыдущего, и условная вероятность совпадает обычной вероятностью:
p A B p A B p B p A( | ) ( ) / ( ) ( )
,
то есть вероятность совместной реализации двух независимых событий вычисляется про-
стым перемножением вероятностей событий-сомножителей:

Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
8
p A B p B p A( ) ( ) ( )
.
События являющиеся независимыми в описанном выше смысле называют статистиче-
ски независимыми. Из приведенного определения сразу следует формула для вероятности
произведения любого числа статистически независимых совместных событий:
)()()()(
2121 nn
ApApApAAAp
.
Приведем несколько примеров вычисления вероятностей статистически независимых со-
бытий.
Вероятность для числа успехов в серии независимых испытаний с двузначным исходом
(биноминальное распределение).
Рассматривается случайный эксперимент, состоящий из конечной серии независимых ис-
пытаний с двузначным исходом «успех – неудача» (этот случайный эксперимент также
называют испытаниями Бернулли). Обозначим вероятность успеха в отдельном испыта-
нии
p
, а вероятность неудачи
q p 1
. Требуется вычислить вероятность появления в
серии длины
n
заданного числа успехов
nk 0
.
Так как отдельные испытания в серии независимы, вероятность появления в серии задан-
ного числа успехов
k
равна произведению
k
вероятностей успеха и
kn
вероятностей
неудачи.
Для вычисления искомой вероятности это число необходимо умножить на число возмож-
ных вариантов появления
k
успехов в серии длины
n
. Это число равно числу возможных
размещений
k
одинаковых объектов по
n
позициям и равно
k
n
C
k
knnnn
!
)1()2)(1(
.
Следовательно, искомая вероятность равна
)!(!
!
;)(
knk
n
CqpCkP
k
n
knkk
nn
.
Вероятность появления серии заданной длины при независимых испытаниях до появления
первого успеха (геометрическое распределение).
Пространство событий в рассматриваемом случайном эксперименте, это последователь-
ности вида
уннн
n
1
(см. подробности в рассмотренном ранее примере).
Поскольку испытания в серии независимы, а успех в последовательности событий всегда
находится на последнем месте, вероятность реализации серии испытаний длины
n
вычис-
ляется как произведение вероятностей
n 1
неудачи и одной вероятности успеха:
P n q p n
n
( ) ; ; ; ;
1
1 2 3
Когда события последовательности не являются статистически независимыми, вычисле-
ние вероятности последовательности событий следует проводить по формуле, исполь-
зующей понятие условной вероятности:
)()|()|(
)()|()(
33221
22121
nnn
nnn
AApAAApAAAp
AApAAApAAAp
Важным частным случаем этой формулы является ситуация, когда входящие в нее услов-
ные вероятности зависят только от события непосредственно предшествующего послед-
нему событию в последовательности
Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
9
);|()|( );|()|(
32322121
AApAAApAApAAAp
nn
Тогда вероятность последовательности событий
)()|()|()|(
)()|()|()()|()(
13221
3322122121
nnn
nnn
ApAApAApAAp
AApAApAApAApAApAAAp
Входящие в последнюю формулу условные вероятности
p A A
k k
( | )
1
удобно трактовать как
вероятности перехода системы из состояния
A
k
в состояние
A
k 1
, что удобно использо-
вать при вычислении вероятностей, подобно тому, как это сделано в следующем примере.
Суммирование по путям.
Программа экзамена состоит из
n2
задач. Студент умеет решать только
n
из них. Эк-
заменационный билет содержит пять задач. Какова вероятность сдать экзамен, если
для этого требуется выполнение одного из трех условий: 1) решено не менее четырех за-
дач из билета; 2) решено три задачи из билета и одна дополнительная из оставшихся;
3) решено две задачи из билета и две дополнительных из оставшихся.
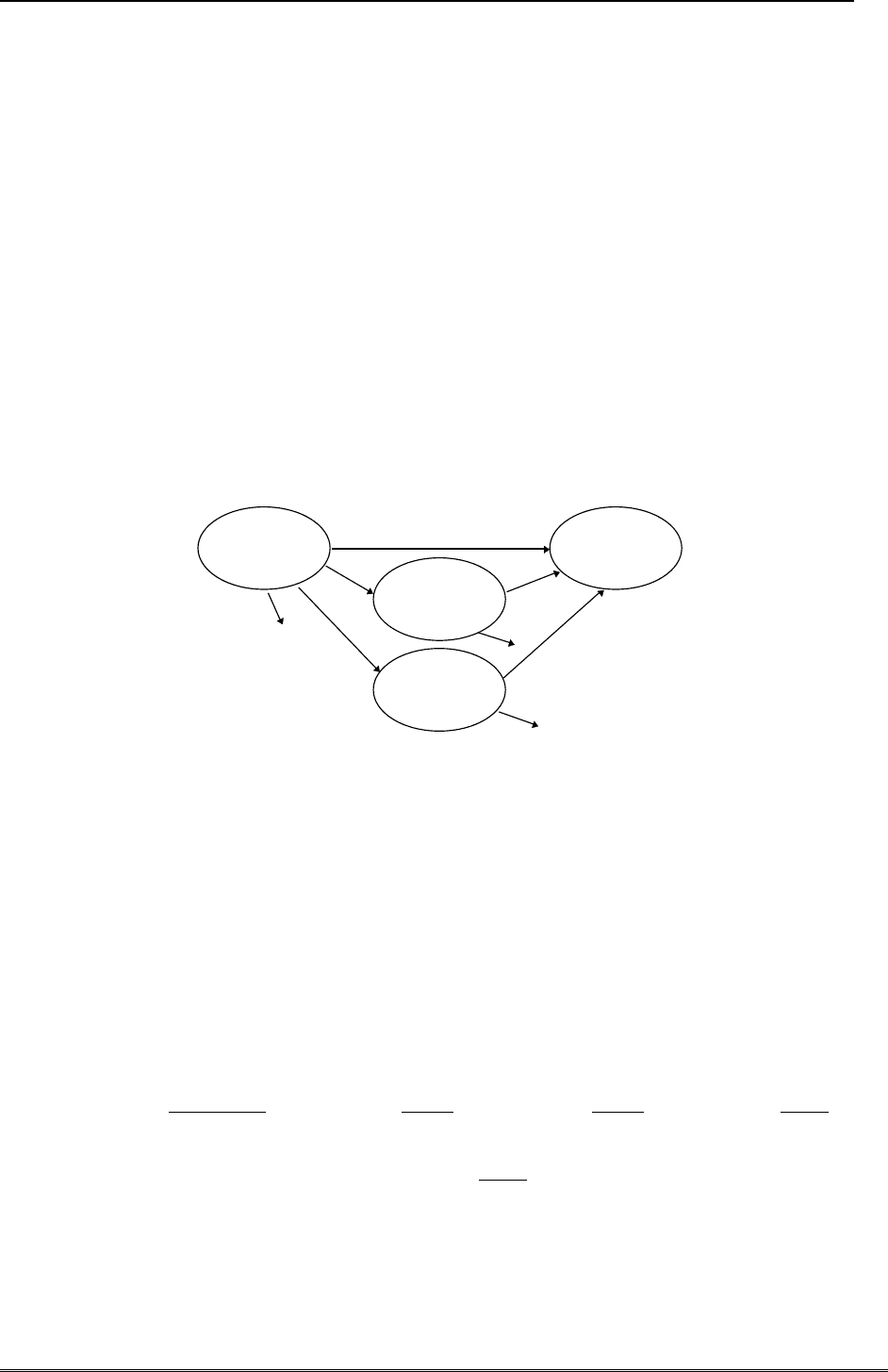
Решение задачи удобно начать с построения схемы перехода студента из исходного со-
стояния в конечное состояние, - возможных путей сдачи экзамена (смотри рисунок).
А
Начало
С
Решено три
D
Решено две
В
Сдано
Каждому пути, ведущему в конечное состояние «сдано» соответствует своя вероятность.
Поскольку пути не имеют точек пересечения, полная вероятность сдать экзамен склады-
вается из суммы вероятностей соответствующих различным путям перехода из состояния
«начало» в состояние «сдано»:
)()()()()()( BDPDАPBCPCAPBAPсданоP
.
Входящие в выписанную формулу вероятности вычисляются на основе постулата равной
априорной вероятности как отношения числа благоприятных исходов к полному числу
исходов, которые определяются по условиям перехода из одного состояния в другое. При
этом зависимость событий формирующих отдельный путь проявляется при подсчете ве-
роятностей через изменение пространства событий в результате «попадания» студента в
промежуточное состояние:
5
2
145
)(
n
nnn
C
CCC
BAP
,
5
2
23
)(
n
nn
C
CC
CAP
,
5
2
32
)(
n
nn
C
CC
DAP
,
1
52
1
3
)(
n
n
C
C
BCP
,
2
52
2
2
)(
n
n
C
C
BDP
Формула полной вероятности и формула Байеса
Пусть событие
A
может произойти только как следствие некоторого другого события,
входящего в набор вызывающих его альтернативных причин
H H H
n1 2
, ,
. Поскольку
причина реализуется ранее следствия, событие-произведение
A H
k
формулируется сле-

Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
10
дующим образом: «
A
происходит по причине
H
k
». Вероятность этого события может
быть вычислена по известной априорной вероятности появления причины
p H
k
( )
и по ап-
риорной условной вероятности
p A H
k
( | )
:
p A H p A H p H
k k k
( ) ( | ) ( )
.
Будем считать, что набор причин образует полную систему, то есть событие
A
может
быть обусловлено только какой либо из перечисленных причин. Иными словами, если со-
бытие
A
произошло, то произошло какое-то из событий
H
k
, то есть событие
k
kH
H
является достоверным. Тогда полная вероятность реализации события
A
безотносительно
к вызвавшей его причине будет вычисляться по формуле, называемой формулой полной
вероятности:
p A p A H p A H p H
k
k
k k
k
( ) ( ) ( | ) ( )
.
Смысл формулы полной вероятности следующий. Поскольку причины вызывающие со-
бытие
A
являются альтернативными
H H
j k
, то событие
A
представляется в виде
суммы полной системы альтернативных событий вида
A H
k
k
k
k
kH
HAHAAA
.
Определение условной вероятности и формула полной вероятности позволят решить зада-
чу об определение так называемых апостериорных условных вероятностей
p H A
k
( | )
, в
которых причина и следствие меняются местами. Смысл понятия апостериорной условной
вероятности состоит в следующем. Событие
A
считается уже произошедшим и ставится
вопрос: какова вероятность того, что событие
A
было обусловлено причиной
H
k
?; то
есть апостериорная условная вероятность связана с «прогнозом вспять», - причина и след-
ствие располагаются в обратной временной последовательности.
Вычисление апостериорной условной вероятности проводится по стандартной формуле,
определяющей условную вероятность:
p H A
p H A
p A
k
k
( | )
( )
( )
.
Поскольку
H A A H
k k
, требуемая апостериорная вероятность может быть вычислена
по известным априорным вероятностям по формуле, называемой формулой Байеса:
p H A
p A H
p A
p A H p H
p A H p H
k
k k k
k k
k
( | )
( )
( )
( | ) ( )
( | ) ( )
.
где для вычисления вероятности
)(Ap
использована формула полной вероятности.
Задача выборочного контроля.
Число бракованных изделий в партии из 100 штук с равной вероятностью может со-
ставлять 0,1,2,3. Пригодной считается партия, не содержащая бракованных изделий.
Для контроля пригодности партии из нее берут для проверки наугад 10 изделий. Если
среди проверенных изделий нет бракованных, партия считается пригодной. Можно ли
считать используемую схему контроля удовлетворительной?
Вводим в рассмотрение следующую систему событий:
H
k
партия содержит
k
бракован-
ных изделий;
A
контрольная партия не содержит бракованных изделий;
k
HA
проверка

Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
11
партии, содержащей
k
бракованных изделий брака не выявила. Согласно исходному ус-
ловию задачи вероятности
P H
k
( ) / 1 4
. Априорные условные вероятности
P A H
k
( | )
вы-
числяем с использованием постулата равной априорной вероятности по формуле:
P A H C C
k k
( | ) /
100
10
100
10
.
Вероятность отсутствия ошибки равна апостериорной вероятности
P H A( | )
0
, которая вы-
числяется по формуле Байеса
P H A
P A H P H
P A H P H
С
С С С С
k k
k
( | )
( | ) ( )
( | ) ( )
,
0
0 0
0
3
100
10
100
10
99
10
98
10
97
10
0 29
.
Поскольку вероятность ошибки контроля
1 0 71
0
P H A( | ) ,
велика, исследуемую схему
контроля, по-видимому, удовлетворительной считать нельзя.
Случайные величины
Случайной величиной называется числовая функция на пространстве событий, - одно-
значное соответствие между элементами пространства событий и значениями случайной
величины (соответствия, при которых нескольким различным событиям сопоставляется
одно и то же число допускаются принятым определением).
Случайные величины подразделяются на дискретные и непрерывные, в зависимости от
типа пространства событий, на котором они определены и области значений, принимае-
мых случайной величиной. При этом важно понимать следующий принципиальный мо-
мент. На непрерывном пространстве событий можно определить случайную величину,
принимающую дискретные значения, но невозможно определить непрерывную случай-
ную величину на дискретном пространстве событий
Понятие случайной величины является важным для приложений потому, что во многих
вероятностных задачах события допускают ясную формулировку в терминах числовых
значений, принимаемых случайными величинами.
Для случайных величин будут использоваться обозначения со шляпкой, а для числовых
значений, принимаемых случайной величиной - тот же символ без шляпки (
x
читается
«случайная величина икс», а
x
- «значение случайной величины икс»).
Функции распределения и плотности вероятностей
Функцией распределения случайной величины называется вероятность события
xx
ˆ
:
)
ˆ
()(
ˆ
xxPxF
x
.
По известной функции распределения можно вычислить вероятность попадания случай-
ной величины в любой заданный интервал:
)()()
ˆ
()
ˆ
()
ˆ
(
ˆˆ
aFbFaxPbxPbxaP
xx
.
Непосредственно из определения функции распределения случайной величины, следуют
ее основные свойства:
)()( yFyxF
функция распределения неубывающая функция;
1)( F
вероятность достоверного события равна единице;
0)( F
вероятность невозможного события равна нулю.

Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
12
Для дискретных случайных величин функция распределения обладает свойством непре-
рывности слева, смысл которого состоит в скачкообразном изменении значения функции
распределения при переходе через очередное значение случайной величины:
F x F x P x
x i x i i
( ) ( ) ( ) 0
.
В силу этого свойства график функции распределения дискретной случайной величины
имеет вид ступенек.
Для непрерывных случайных величин функция распределения обладает свойством диф-
ференцируемости, отражающим возможность вычисления для непрерывной случайной
величины вероятности ее попадания в сколь угодно малый интервал:
)()( ;)()()()
ˆ
(
ˆˆˆˆˆ
xFxdxxxFdxxFdxxxxP
xxxxx
.
Входящая в выписанную формулу производная функции распределения называется плот-
ностью вероятности непрерывной случайной величины.
1
Суммируя свойства функций распределения, приходим к формулам для вычисления зна-
чений функции распределения дискретных и непрерывных случайных величин по вероят-
ностям появления конкретного значения дискретной случайной величины
P x
i
( )
или по
известной плотности вероятности непрерывной случайной величины:
F x P x F x z dz
i
x x
x
i
( ) ( ), ( ) ( ) .
{ }
Моменты и характеристические функции случайных величин
Моментом случайной величины порядка
N
называется среднее значение
N
-й степени
рассматриваемой случайной величины:
M x x P x
N
i
N
i
x
[ ] ( )
{
}
,
M x x x dx
N N
[ ] ( )
.
(формула с суммированием относится к дискретным случайным величинам, а формула с
интегрированием, - к непрерывным случайным величинам). Смысл термина «среднее зна-
чение» очевиден из структуры выписанных формул, - суммируются значения случайной
величины, умноженные на вероятность реализации этого значения
2
.
Наиболее часто приходится иметь дело с моментами низших порядков. Момент нулевого
порядка есть просто условие нормировки вероятности:
}
ˆ
{
0
1)(]1[][
x
i
xPMxM
,
dxxxM )(][
0
.
Момент первого порядка называется средним значением случайной величины:
1
Понятие плотности вероятности может быть обобщено на дискретные случайные величины при помощи
дельта - функции Дирака:
( ) ( ) ( )x P x x x
i
x
i
i
. Это позволяет рассматривать многие свойства слу-
чайных величин без разделения на дискретные и непрерывные. Однако, на начальном этапе изучения целе-
сообразно раздельно выписывать формулы для дискретных и непрерывных случайных величин.
2
Выписанные средние значения от функций случайных величин называют также средними по вероятности
и математическими ожиданиями.

Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
13
}
ˆ
{
)(][
x
ii
xPxxM
,
dxxxxM )(][
.
Комбинация моментов первого и второго порядка
D x M x M x[ ] [ ] [ ]
2 2
называется дисперсией случайной величины, которая характеризует разброс значений
случайной величины около среднего значения. Дисперсия неотрицательна, что легко уви-
деть из тождества:
( [ ]) ( ) ( [ ] [ ]) ( )
( ) [ ] ( ) [ ] ( ) [ ] [ ] [ ],
{
} {
}
{
} {
}{
}
x M x P x x x M x M x P x
x P x M x x P x M x P x M x M x D x
i i
x
i i i
x
i i i i
x
i
xx
2 2 2
2 2 2 2
2
2
или аналогичного тождества для непрерывных случайных величин.
Для измерения разброса значений случайной величины около среднего значения также
используется так называемое стандартное (или среднеквадратичное) отклонение:
[ ] [ ]x D x
, которое имеет ту же физическую размерность, что и величина
x
.
Характеристической функцией случайной величины называется среднее значение показа-
тельной функции следующего вида:
{
}
( ) exp( ) ( )
x i i
x
ix P x
,
( ) exp( ) ( )
x
ix x dx
.
Разложение показательной функции в ряд Маклорена по степеням переменной
ix
при-
водит к связи между характеристической функцией и моментами случайной величины:
00 }
ˆ
{}
ˆ
{ 0
ˆ
][
!
)(
)(
!
)(
)(
!
)(
)(
N
N
N
N x
i
N
i
N
x N
i
N
i
N
x
xM
N
i
xPx
N
i
xPx
N
i
,
000
ˆ
][
!
)(
)(
!
)(
)(
!
)(
)(
N
N
N
N
N
N
N
N
N
x
xM
N
i
dxxx
N
i
dxxx
N
i
.
Следовательно, зная характеристическую функцию случайной величины можно получить
все моменты при помощи связи между коэффициентами ряда Маклорена с производными:
M x i
d
dx
N N
N
N
[ ] ( )
( )
|
0
,
и наоборот: зная все моменты случайной величины можно записать ее характеристиче-
скую функцию в виде ряда.
Примеры характеристических функций
Биноминальное распределение.
Случайная величина
N
число успехов в серии испытаний Бернулли длины
N
принимает
дискретные значения
k N 01 2; ; ; ;
с вероятностями
P k C p q
N N
k k N k
( )
. Характеристиче-
ская функция вычисляется при помощи формулы бинома Ньютона:
( ) ( ) exp( ) exp( ) ( exp( ))
N
N
k
N
N
k
k
N
k N k N
P k i k C i k p q q p i
0 0
.

Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
14
Для одного испытания характеристическая функция имеет вид:
( ) exp( )
n
q p i
, то
есть характеристическая функция числа успехов в серии равна произведению характери-
стических функций числа успехов в каждом отдельном испытании. Это является отраже-
нием того факта, что случайная величина
N
число успехов в серии является суммой ста-
тистически независимых случайных величин:
N n
i
i
N
1
- чисел успехов в отдельных ис-
пытаниях серии, каждое из которых принимает два значения: 0 (неудача) и 1 (успех).
Низшие моменты для числа успехов вычисляются по характеристической функции разло-
жением в ряд с точностью до второго порядка, с использованием известных разложений
показательной функции и бинома:
)(
2
)(
1
))
2
)(
(1())1)(exp(1())exp((
22
2
2
NppqN
i
pNi
i
ipipipq
NNN
.][ ;][ ;][ ;][
222
pqNNpqNNDNppqNNMpNNM
Геометрическое распределение.
Это распределение используется для вычисления вероятности появления серии заданной
длины
n
в неограниченных сериях испытаний до появления первого успеха:
;3;2;1 ;1 ;)(
1
nqppqnP
n
.
Характеристическая функция случайной величины
n
вычисляется при помощи формулы
суммирования геометрического ряда
( ) exp( ) exp( ) exp( )
exp( )
exp( )
q p iN p i q p ik
p i
q i
n
n
k
k
1
1 0
1
.
Разлагая характеристическую функцию в ряд, получаем первые моменты:
),/1/2(
2
)(
)/1(1))2/)()(/1(1(
)1))(exp(/1(1(
)1()1)(exp()exp()exp(1
)exp(
2
2
12
1
pp
i
piiip
ip
qi
p
qi
p
iq
ip
./]
ˆ
[ ;/]
ˆ
[ ;//1]
ˆ
[ ;/1]
ˆ
[
2222
pqnpqnDpqpnMpnM
Распределение Пуассона.
Это распределение используется для описания случайной величины
k
ˆ
, принимающей
значение из натурального ряда
k 0 1 2 3 , , , ,
. Вероятность появления конкретного
значения распределенной по Пуассону случайной величины определяется формулой:
P k
k
k
k
( )
!
exp( ); , , , 0 1 2
.
Параметром распределения Пуассона , как будет видно ниже, является ее первый момент
(среднее значение) случайной величины.
Характеристическая функция вычисляется при помощи известной формулы разложения
показательной функции в ряд Маклорена:
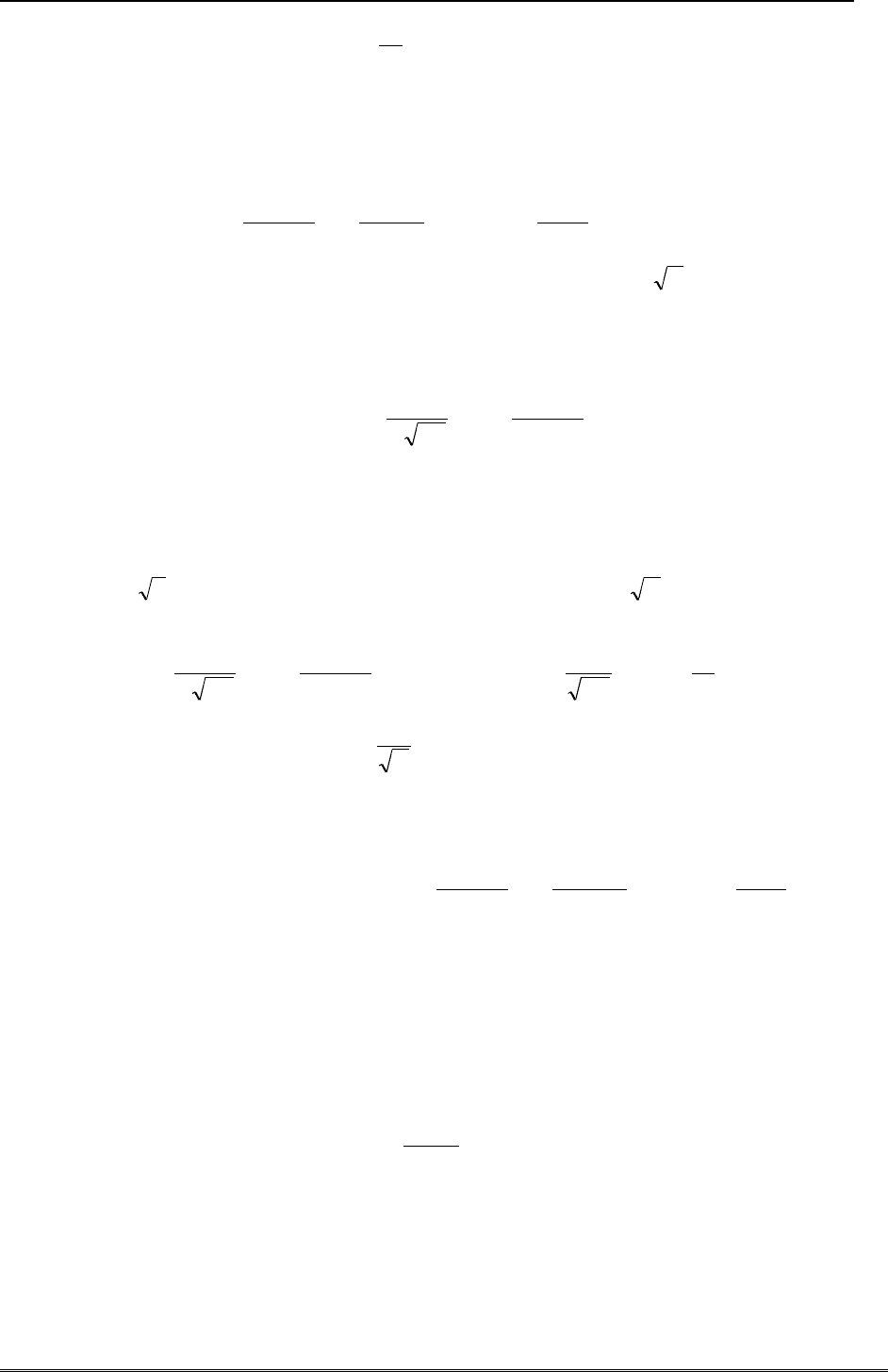
Начальные сведения по теории вероятностей
Кафедра высшей математики КузГТУ Конспекты проф. Д. В. Алексеева
15
))1)(exp(exp()exp(
!
)exp()(
0
iki
k
k
k
.
Разложение характеристической функции в ряд с точностью до второго порядка дает
формулы для низших моментов, дисперсии и стандартного отклонения:
),(
2
)(
1)
2
)(
1)(
2
)(
1(
)2/)exp(()exp())2/)((exp())1)(exp(exp()(
2
2222
22
i
i
ii
i
iiiii
][ ;][ ;][ ;)(
22
KKDKMKM
.
Нормальное распределение.
Непрерывная случайная величина, с плотностью вероятности
2
2
),(
2
)(
exp
2
1
)(
ax
x
a
,
называется распределенной по нормальному закону со средним значением а и стандарт-
ным отклонением
. Нормальное распределение обозначают символом
N a( , )
, а его ха-
рактеристическая функция вычисляется при помощи замен переменных
/)( axz
,
2/)(
izu
и известного интеграла Гаусса
exp( )
u du
2
:
).2/exp()exp()exp(
1
)2/exp()exp(
2
exp
2
1
)exp(
2
)(
exp
2
1
)(
22222
2
2
2
),(
iaduuia
dzzi
z
iadxix
ax
a
Вычисление моментов, дисперсии и стандартного отклонения проводятся при помощи
разложения показательных функций в ряд до квадратичных слагаемых:
)(
2
)(
1 )
2
)(
1)(
2
)(
1()2/exp()exp()(
22
22222
22
),(
a
i
ai
iai
aiia
a
,
.][ ;][ ;][ ;][
2222
xxDaxMaxM
Отсюда ясен смысл названия параметров нормального распределения.
Гамма-распределение.
Непрерывная случайная величина, принимающая неотрицательные значения имеет гамма-
распределение с параметрами (a,b) если ее плотность вероятности:
)exp(
)(
)(
1
bx
a
xb
x
aa
,
где
0
1
)exp()( duuua
a
, гамма-функция Эйлера.
Характеристическая функция гамма-распределения вычисляется при помощи определения
гамма-функции и замены переменной
u x b i ( )
в интеграле:
