Воронов А.А. Теория автоматического управления. Часть первая

Подождите немного. Документ загружается.

Вещественные и мнимые частотные функции системы опре-

деляются равенствами

U (со) — А (со) cos ф (со);

V (со) = А (со) sin ф (со).

Пользуясь полученными соотношениями

можно построить АФЧХ. Из (2.55) очевидно

(2.57)

(2.55)—(2.57),

L (со)

i— 1

И.

(2.58)

где L (со) — 20 lg А (со) и L

(со) = 20 lg Л^ (со) — логарифми-

ческие амплитудные частотные функции.

Из (2.56) и (2.58) вытекает следующее правило построения

J14X (ЛАЧХ и ЛФЧХ) систем, передаточные функции кото-

рых преобразованы к виду (2.54): строят ЛЧХ отдельных

звеньев и затем их графически складывают.

На основании (2.58) можно также сформулировать несколь-

ко иной, более простой порядок построения ЛАЧХ. Проил-

люстрируем это сначала на кон-

кретном примере.

Пусть W (s)=

100

(s+l)/№ х

X (10s + 1) (0,01 s

+0,1 s+1)].

J1 огар ифмическа я ам пл итуд-

ная частотная функция

(о>) =г

40—v20 lgo)—

—20 lgj/"(10o))

+20 igy-^Ti-

- 20 lg |/(

—

0,01 со

)

(0,1 со)

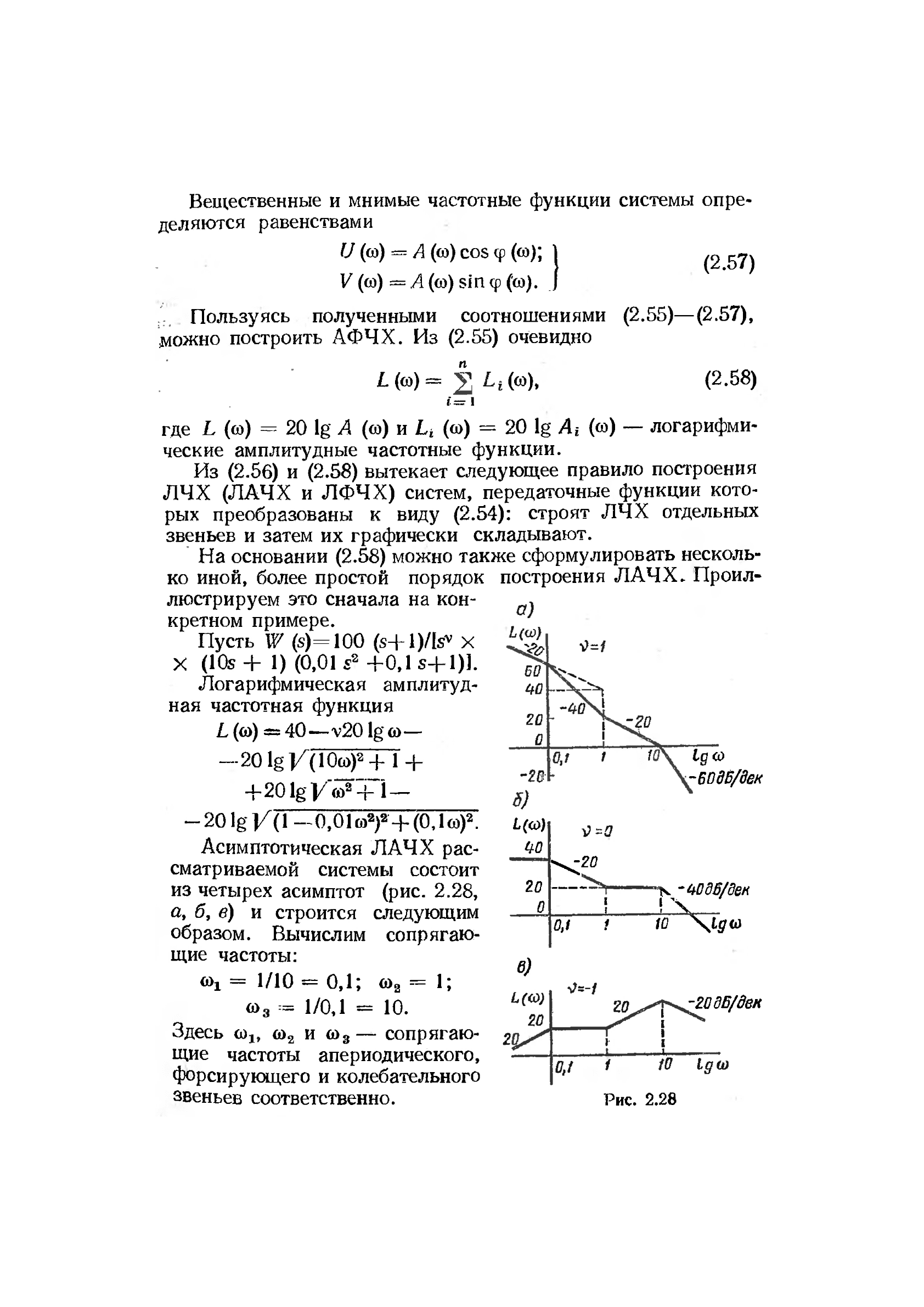
Асимптотическая ЛАЧХ рас-

сматриваемой системы состоит

из четырех асимптот (рис. 2.28,

а, б, в) и строится следующим

образом. Вычислим сопрягаю-

щие частоты:

о)! = 1/10 - 0,1; б>

- 1;

- 1/0,1 - 10.

<о

-ШБ/дек

L(<o)

-^zo

—у<-Мд6/дек

X -

i f

10 \l gio

О)

-20 дБ/дек

Здесь со

о>2 и

о) з —-

сопрягаю-

щие частоты апериодического,

форсирующего и колебательного

звеньев соответственно.

Рис. 2.28

Напомним, что при построении асимптотической ЛАЧХ эле-

ментарных звеньев при частотах, меньших сопрягающей час-

тоты, под корнем оставляют только единицу (остальными чле-

нами пренебрегают), а при частотах, больших сопрягающей

частоты, —члены с найвысшей степенью со. Поэтому в рас-у

сматриваемом примере при

о>

<; со

L (со) « 40 — v201gco.

Это уравнение первой асимптоты. Согласно этому уравне-

нию, первую асимптоту проводят через точку с координата-

ми 1 и 20 lg k с наклоном — v20 дБ/дек. Она кон-

чается на первой сопрягающей частоте.

При % ^ о < ш

аналогично имеем

L (со) 40 — v201g со — 201g Юсо = 20 — v 20 lgo> —

— 20 lgco.

Это уравнение второй асимптоты. Ее наклон изменяется

на — 20 дБ/дек и обусловливается апериодическим звеном.

Вторую асимптоту проводят от конца первой асимптоты до вто-

рой сопрягающей частоты согласно ее уравнению с наклоном

(— v 20—20) дБ/дек.

При 6>

О) < ш

L (со) « 20 — v201gco— 201gco + 201gco - 20 — vx

X20 Igco.

Это уравнение третьей асимптоты. Ее наклон изменяется

на 20 дБ/дек и обусловливается форсирующим звеном. Третью

асимптоту проводят от конца второй асимптоты до третьей со-

прягающей частоты с наклоном — v-20 дБ/дек.

При со > со

L (со) = 20 — v-20lgco — 40 lg

0,1 со

- 60 — v201gco —

— 401g со.

Это уравнение последней, четвертой, асимптоты. Ее наклон

изменяется по отношению к третьей асимптоты на —40 дБ/дек

и обусловливается колебательным звеном.

Теперь нетрудно сформулировать общее правило построе-

ния асимптотической ЛАЧХ системы с передаточной функци-

ей вида

1= 1

где Wi (s) — передаточные функции элементарных звеньев.

Правило построения асимптотической ЛАЧХ.

1. Вычисляют сопрягающие частоты и значение 201g&,

где k — передаточный коэффициент системы, равный произ-

ведению передаточных коэффициентов звеньев (k = П&

2. Строят первую асимптоту, которую проводят До первой

сопрягающей частоты через точку с координатами о) = 1 и

L — 201gfe с наклоном — v*20 дБ/дек. Здесь v равно разности

между числами интегрирующих и дифференцирующих звень-

ев.

3. Проводят вторую асимптоту от конца первой асимптоты

до второй сопрягающей частоты. Ее наклон изменяется на

20,-20, 40 или — 40 дБ/дек в зависимости от того, является

ли с&л сопрягающей частотой форсирующего, апериодическо-

го, форсирующего второго порядка или колебательного зве-

на соответственно.

4. Строят каждую последующую асимптоту аналогично

второй. Изменение наклона (I + 1)-й асимптоты зависит

от того, сопрягающей частотой какого элементарного звена

является щ.

Если какая-либо сопрягающая частота является кратной

и ее кратность равна /, т. е. имеется I одинаковых элементар-

ных звеньев,*то изменение наклона при этой частоте в I раз

больше, чем при соответствующей простой частоте.

Для колебательных звеньев с малым коэффициентом демп-

фирования <с 0,4) асимптотическая ЛАЧХ должна быть

скорректирована в окрестности сопрягающей частоты по точ-

ным формулам или с помощью кривых поправок (см. рис. 2.9, г).

§ 2.8. Многомерные стационарные линейные

системы

Многомерными системами или системами многосвязного уп-

равления называют автоматические системы управления, в ко-

торых имеется несколько (больше одной) управляемых вели-

чин. Соответственно объекты, имеющие несколько управляе-

мых величин, называют многомерными объектами или объ-

ектами многосвязного управления.

Примерами многомерных объектов могут быть: самолет,

у которого управляемыми величинами являются курс, углы

тангажа и крена, высота, скорость; паровой котел, в котором

регулируется температура, давление пара и другие величины.

Обычно управляемые величины называют выходами или

выходными величинами. И поэтому многомерные системы еще

определяют как автоматические системы с многомерным (век-

торным) выходом.

Многомерные системы и объекты называют линейными и

стационарными, если они описываются системой линейных

дифференциальных уравнений с постоянными коэффициента-

ми.

Уравнения многомерных стационарных линейных систем

и объектов. Пусть у

..., у

обозначают выходные величины,

Hi, и

— параметры управления или задающие воздейст-

вия и Д, f

— возмущающие воздействия. Уравнения

многомерных стационарных линейных систем и объектов в об-

щем случае можно записать в виде следующей системы:

Яп

(р)Уг

+ —+ «1Р

(Р)Уо

= йи (Р)н

+ ... +b

(р) u

+ (p)fi + ... + c

(p) f ,

(p) Ух

+... +

^pp (P) yp

= b

i(p)u

+ ... + b

(P)

-f

+ + —+ {p)fb

или в более компактной форме

р т I

u(P)yj^ 2 Ь

(р)и

}

+ 2 c

(p)f;,

р. (2.59)

/= | /=

Здесь aij (р), Ь

(р), c

j (р) обозначают стационарные линей-

ные операторы, т. е. полиномы от оператора дифференцирова-

ния с постоянными коэффициентами.

Переходя в обоих частях (2.59) к изображениям Лапласа,

при нулевых начальных условиях получим систему алгебраи-

ческих уравнений:

р m I

2 а

(s)

}

(s)

= 2 btj

(s)

Uj (s) + 2

(*)

(

i /-= i /= i

i = l....,p, (2-60)

где

Yj (s) = L{y

}

(t)}, U

(s) = L{u

}

(t)), F

}

(s) = L {/,- (0).

Для многомерных систем удобна матричная форма записи

уравнений.

Введем в рассмотрение матрицы

Уi~\

•

; Ш =

«и (Р)

...

Clip

(р)

-1

. «р! (Р)

••• «рр (р)

J 1

L«m.

В(р)

Ьц

(/>)...

1т

{р)

\\ {р)...Ь

рт

(р)

f =

; с м-

^11 (/>)•••

^п(р)

^piH-.^PHp).

С их помощью (2.59) в матричной форме будет

A(p)y = B(p)u + C(p)f.

(2.61

Точно так же можно записать (2.61) в изображениях Лап-

ласа в матричной форме:

A (s)

Y (s)

- В (s) U (s) + С (s) F (s).

Здесь

(2.62)

«п («)... aip(s)

A (s) =

|; Y (s)

«pi (s)...«pp(s)

(s)...b

(s)

]

у As)

IVp (si

(s) =

bf>\

(s)... bp

(s)

1 'Л (s) c

(s)... c

(s)

<s) = i

; с (s) = ; F(S) =

•

L^m(s).

Cpl (s)...

Cp/

(s) _

В (2.61), после умножения и сложения матриц, в правой и

левой частях получатся матрицы-столбцы. Приравняв их со-

ответственные элементы, получим систему уравнений (2.59).

Аналогично, выполнив указанные операции над матрицами

и приравняв соответственные элементы матриц левой и правой

Частей матричного уравнения (2.62), получим систему (2.60).

Пример 2.6. Пусть исходная система дифференциальных урав-

нений имеет вид

(ао P

) у

У2

= К №

аз

У1+(^р +

) Уг

= Ь

В матричной форме, как нетрудно проверить, эта система записывается

в виде

{р)

у = В (/?) и,

где

А {р)

-I

+ а

аз а&р+с1ь

} '«-[*.' л]

Г: а

Передаточная матрица. Для описания многомерных систем

и объектов, как и в случае одномерных систем, можно ис-

пользовать передаточные функции. Передаточной функцией

W/J. (s) (в изображениях Лапласа) по /-му параметру управле-

ния и i-му выходу называют отношение изображения Лапласа

выходной величины у

к изображению входной величины

при

нулевых начальных условиях. По определению,

{s)^Y

(s)/U

(s). (2.63)

Эту передаточную функцию можно вычислить следующим об-

разом. В системе (2.60) приравниваем нулю изображения всех

возмущающих воздействий и параметров управления, кроме

Uj (s). Из полученной системы алгебраических уравнений на-

ходим решение Yi (s), а затем, разделив его на Uj (s), получим

искомую передаточную функцию.

Аналогично определяют передаточную функцию w\§ (s)

по /-му возмущающему воздействию и i-му выходу:

(

)

(2.64)

В случае многомерных систем (объектов) для ее полного

описания необходимо иметь р-т передаточных функций по уп-

равлению и fj-/ передаточных функций по возмущению. Эти

передаточные функции записывают в виде матриц:

(s)

Wf (s) -

w«

(s)...

Wlm (S)'

Wlv

(s)...

(s)J'

(s)...

(s) 1

•

wU (s)...

(s)

(2.65)

(2.66)

Матрицы (2.65) и (2.66) называют матрицами передаточ-

ных функций или

передаточными

матрицами: матрица (2.65)—

по управлению,, а матрица (2.66) — по возмущению.

Передаточные матрицы дают полное описание многомерных

систем (объектов) при нулевых начальных условиях. С их по-

мощью уравнения (2.60) или (2.62) многомерной системы в изо-

бражениях Лапласа можно записать в следующем виде:

Y (s)

- W"

(s)

-h Wf

(s)

(s).

(2.67)

Действительно, согласно определению (2.63), когда изоб-

ражения всех возмущающих воздействий и параметров уп-

равления, кроме Uj (s), равны нулю, имеем

(s)=^Wl(s)U

(s)

р; / = га.

Аналогично, из (2.64)

(s) = W

(s) Fj (s), t-1 p;/«l /.

В общем случае, когда все параметры управления и возмущаю-

щие воздействия отличны от нуля, используя принцип супер-

позиции, можем записать

т I

Yi(s)=: 2 П (№(*> + S

р. (2.68)

/=1 /=1

Очевидно, (2.67) является матричной формой записи получен-

ной системы (2.68).

Рассмотрим способы вычисления передаточных матриц.

Первый способ, указанный выше, основан на использовании

определений (2.63) и (2.64). Второй способ основан на соотно-

шениях

(s)

= A

(s) В

(s); W

(s)

- А-

($) С (s).

(2.69)

Эти соотношения получают следующим образом. Умножим

слева обе части матричного уравнения (2.62)

(s) Y (s)

В (s) U (s)

(s)F(s)

на обратную матрицу A*"

(s). Тогда получим

(s) « A-

(s) В

(s)

U (s) 4- A-

(s) С

($)

F (s).

Приравнивая правую часть полученного уравнения к правой

части равносильного ему уравнения (2.67), получим соотноше-

ния (2.69).

Как известно из курса высшей алгебры, обратная матрица

Ли (s)... i4i

(s)

A -

(s)=

|A(s)f

(s)... App(sy

Здесь A

(s) — алгебраическое дополнение элемента а

(s).

Знак Т обозначает операцию транспонирования.

Пример 2.7. Пусть система (объект) описывается уравнениями

Перейдем к изображениям Лапласа (при нулевых начальных условиях)

(s* + s) У

(s)

У 2

) = Vi

(s)

+ F,

(s);

(s + 1) Y

(s) + sY

(S) - U

(s) + F

(s).

В Матричной форме эта система записывается так:

(s)

Y (s)

—

(s)

U (s) +

(s) F (s),

где

+ s 11

Г! 0] П 01

A(S)

= ls+I J

5 B(S) =

|o .J

: C<S)

= lo ,]•

Найдем обратную матрицу A^

(s):

I A

(s)

I — (s

+ 1) (s

—

1); A

=s; A,= —(s+1);

(s+ 1) (s

—

1) L —

+ s \

-—

— f

I-

Так как В (s) и С (s) являются единичными матрицами, то

(s)-A-i(s).

Весовые или импульсные переходные матрицы. Пусть уп-

равляющий параметр Uj = б (/), а остальные управляющие

параметры и возмущающие воздействия равны нулю. При этом

решение (2.59) многомерной системы при нулевых начальных

условиях обозначим

(t), (0,..., ^р/ (0- Эти функции

называют весовыми или импульсными переходными функция-

ми. Функция (£) описывает реакцию системы на i-u вы-

ходе при действии в точке приложения у-го параметра управле-

ния единичного импульса и называется импульсной переходной

или

весовой

функцией по /-му параметру управления и i-му вы-

ходу. Матрицу

[

Wn (/)... wtmi't)

Wpi

(t)...W%

(t)

составленную из весовых функций по управлению, называют

импульсной переходной или

весовой

матрицей по управлению.

Аналогично определяют импульсную переходную или весовую

матрицу по возмущению:

wf (t) =

u(t)... w\t(t)

pl (*)••• Wptit)

Здесь w[j (t)

...,

Wpj

(t) — решение (2.59) многомерной систе-

мы, когда fj = б (t)

а все остальные возмущающие воздейст-

вия и параметры управления равны нулю.

Весовые матрицы, как и передаточные матрицы, дают пол-

ное описание многомерной системы (объекта).

Установим связь между весовыми и передаточными матри-

цами.

Согласно определению (2.63) передаточной функций Wlj

(s)

уi

(«)

= W

(s)

Uj (s),

= 1,..., p. (2.70)

Так как (s) = L{6 (t)} = 1 и y

(/) — w

(t) при uj =

= 6 (?) и остальных входных воздействиях, равных нулю, то

из уравнения (2.70)

оо

B7?,(s) = LK(0)=f w"/(t)e~

dt, (2.71)

• I I

I 1,...,

1 5 . .

. ,

TTb.

Аналогично можно показать, что

оо

\H/(e)=LM/(0i==J w

n(t)e~

р,

(2.72)

Таким образом, передаточные функции (элементы передаточ-

ных матриц) равны изображению Лапласа от весовых функций

(элементов весовых матриц).

В матричной форме (2.71) и (2.72) принимают вид

оо

(s)

- L {w* (t)\ » J w« (t) e~

dt;

со

(s)

L {vtf (0) = J

(0e~

dt.

По определению, интеграл от матрицы равен матрице интегра-

лов от ее элементов.

Запишем формулу для определения выходных величин по

весовым матрицам при произвольных входных воздействиях.

Учитывая, что оригиналами от передаточных функций явля-

ются весовые функции, и используя теорему о свертке, из

(2.68)

т I -

Yi(s) = 2 ^

ii(s)Uj(s)+ 2 W

(s)F

(s),

/==

i /= i

переходя к оригиналам, получим

т оо

Уг

(0= X f

V>%

(t - Т)

(Т) dx +

1 О

l oo

+ S f T)/>(x)dT,

= 1,...., p-

/-1 »

Эта система в матричной форме записывается как

оо оо

У(0= f w

(£—т)и(т)dT+ Г w'(/—T)f(T)dT.

Таким образом, связь между выходными и входными величи-

нами с помощью весовых матриц записывается так же, как и в

одномерном случае.

Запись дифференциальных уравнений в нормальной форме

Коши. При рассмотрении многих вопросов удобно, если урав-

нения одномерных и многомерных систем записаны в виде нор-

мальной системы. Нормальной системой или системой в нор-

мальной форме Коши называют систему дифференциальных

уравнений первого порядка, разрешенных относительно про-

изводных. В частности, нормальной системой линейных диф-

ференциальных уравнений называют систему

п т I

*»•= 2 ацхнь 2

j+ 2

,ея1

(

/=i /=1

В матричной форме она записывается как

х = Ах

-Ь

Bu + Cf, (2.74)