Воронов А.А. Теория автоматического управления. Часть первая

Подождите немного. Документ загружается.

звенья. Звено, которое можно описать уравнением

{Tip'

+ 7\р + 1) у = ku,

или в другой форме

(7V + 2 ITp + l)y = ku

(2.49)

где Т = 7\>, £ == Т

/(2Т)

или передаточной функцией

W (s) - kt (TV + 2ITS + 1), (2.50)

называют колебательным, если 0

<С

£ <С 1, консервативным,

если 1 = 0 (7\ — 0), и

апериодическим звеном

второго порядка»

если § ^ 1. Коэффициент £ называют коэффициентом

демпфирования.

Колебательное звено. (0 < £ < 1). Частотная передаточ-

ная функция

W (/с*) = k/[(\ — Г

со

)+/2£Гсо].

Умножив числитель и знаменатель на комплексно-сопряжен-

ное знаменателю выражение, получим вещественную и мни-

мую частотные функции:

им-..

1"Г* ..; VH-

(1 —ca

)

-h(2§r

<0)

(1—Г

со

)

+ (2|Г(й)

Фазовая частотная функция, как это видно из АФЧХ

(рис. 2.9, а), изменяется монотонно от 0 до — ли выражается

формулой

<р

(со) =

arct

g ,

У2 2

при

со

^ 1/7\

1 —>

_„_

arct

g-l^ при

со

> 1/7\

Логарифмическая фазовая частотная характеристика (рис.

2.9, б) при со -> 0 асимптотически стремится к оси частот, а

при со

—>

оо — к прямой ф = — я. Ее можно построить с

помощью шаблона. Но для этого необходимо иметь набор шаб-

лонов, соответствующих различным значениям коэффициента

демпфирования.

Амплитудная частотная функция

(со)

- ki V(

- Т

со

)

+ (2£Гсо)

логарифмическая амплитудная функция

(со)

- 20 lg £-20 lg}/(1 —Т

со

)

(2£7со)

(2.51)

L(со) ^

Уравнение асимптотической ЛАЧХ имеет вид

20 lg k при

со

20Igk—401gTco при о^Ш!,

где Oi = 1/Г является сопрягающей частотой. Оно получает-

ся из уравнения (2.51), если под корнем при со < о^ оставить

только единицу, а при со^со

—

слагаемое Г

со

. Асимптоти-

ческая ЛАЧХ (рис. 2.9, б) при со < со! параллельна оси час-

тот, а при со ^ со

имеет наклон — 40 дБ/дек.

Следует иметь в виду, что асимптотическая ЛАЧХ (рис.

2.9, б) при малых значениях коэффициента демпфирования до-

вольно сильно отличается от точной ЛАЧХ. Точную ЛАЧХ

можно построить по асимптотической ЛАЧХ, воспользовав-

шись кривыми отклонений точных ЛАЧХ от асимптотических

(рис. 2.9, г).

Решив дифференциальное уравнение (2.49) колебательного

звена при и = 1 (/) и нулевых начальных условиях [у (0) —

= у

{0)

= 01, найдем переходную функцию:

МО

V«

+Pf

_oi

sinflW

+ <p

где a - l/T\ p = V\ -|

/Г;

Фо

= arctg^L^

Весовая функция

w(t)=h (t)

sinj3f.

По переходной характеристике (рис. 2.9, е) можно опреде-

лить параметры колебательного звена следующим образом.

Р)

б) Ш)

ум V,

Ш -AW)

-зс/г

<Ц _ '

Г,

0,2OA 0J5

J 1 3^56

810

Рис. 2.9

О)

J ^

<*>Ч/Т

О к

Рис. 2.10

Передаточный коэффициент к определяют по установивше-

муся значению h (оо) переходной функции. Постоянную вре-

мении Т и коэффициент демпфирования

Е;'

можно найти из

уравнений

или

=•-

2л/Т

; а

—

-~\п

где Т

— период колебаний; А

и Л

— амплитуды двух со-

седних колебаний относительно установившегося значения

(рис. 2.9, в).

Консервативное звено (£ = 0). Передаточная функция

W (s) = k/(T

+ 1).

Частотная передаточная функция

W (/со) - k/( 1 — Г

о>

Фазовая частотная функция, как это следует из АФЧХ

^рис. 2.10, а),

. | 0 при о <

/Т;

[ —л; при со > 1/Т

Это выражение можно получить из фазовой частотной функ-

ции колебательного звена предельным переходом при £ -> 0.

Нетрудно выписать выражения для остальных частотных

функций; ЛЧХ приведены на рис. 2.10, б.

Переходная функция

h(t)=k(\

—

cos

о>!

t);

= 1 /Т

Переходная характеристика (рис. 2.10, в) представляет со-

бой график гармонических колебаний.

Апериодическое звено второго порядка (| ^ 1). Передаточ-

ную функцию (2.50) при £ ^ 1 можно преобразовать к виду

(s)

= - ,

(Tis+\)(T

s+l)

где

1,2

Апериодическое звено второго порядка можно представить

как последовательное соединение двух апериодических звень-

ев первого порядка. Оно не относится к числу элементарных

звеньев.

Форсирующее звено второго порядка. Так называют зве-

но, которое описывается уравнением

У = к (7V + 2ЪТр + I) и

или, что то же, передаточной функцией

W (s) - к (TV + 2ITs + 1) (2.52)

при условии, что 0 ^ I <; 1.

Не представляет трудности получить выражения для час-

тотных и временных функций и построить соответствующие

характеристики.

На рассмотрении этих вопросов останавливаться не будем.

Заметим только, что при частотах, превышающих сопрягают

щую частоту, ЛАЧХ имеет наклон 40 дБ/дек и ЛФЧХ получа-

ется зеркальным отражением относительно оси частот ЛФЧХ

соответствующего колебательного или консервативного звена.

Если £ I, то звено с передаточной функцией (2.52) не отно-

сится к числу элементарных; его можно представить как

последовательное соединение двух форсирующих звеньев пер-

вого порядка.

Неминимально-фазовые звенья. Звено называют мини-

мально-фазовым, если все нули и полюсы его передаточной

функции имеют отрицательные или равные нулю веществен-

ные части. Звено называют неминимально-фазовым, если хотя

бы один нуль или полюс его передаточной функции имеет по-

ложительную вещественную часть.

Напомним, что нулями передаточной функции W (s) —

= R (s)/Q (s), где R (s) и Q (s) — полиномы от s, называют кор-

20Lgk

О.

-Я/2

а)

X2036/дек

1§0)

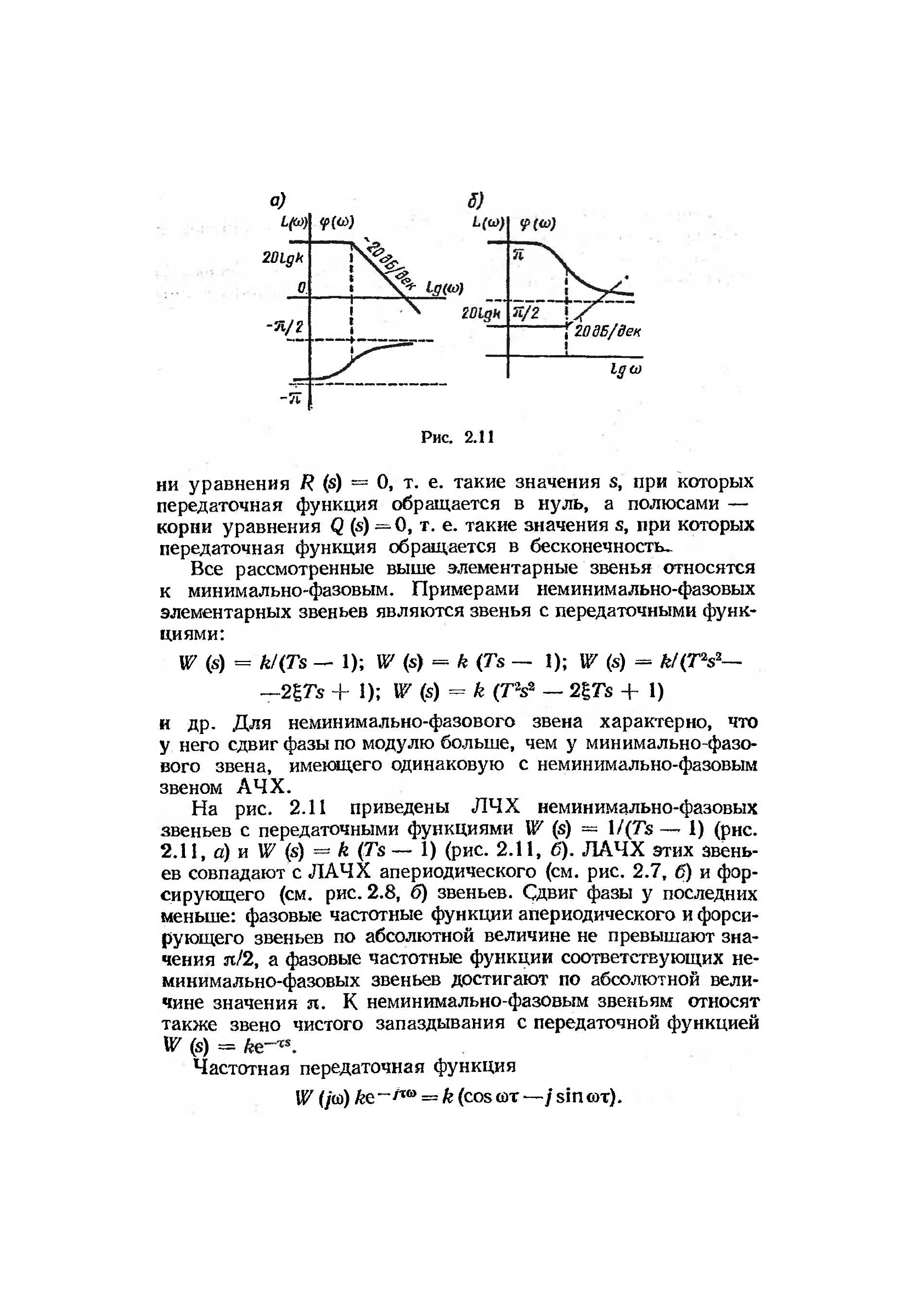
Рис. 2.11

ни уравнения R (s) = 0, т. е. такие значения $, при которых

передаточная функция обращается в нуль, а полюсами —

корни уравнения Q

(s) —

0, т. е. такие значения s, при которых

передаточная функция обращается в бесконечность^

Все рассмотренные выше элементарные звенья относятся

к минимально-фазовым. Примерами неминимально-фазовых

элементарных звеньев являются звенья с передаточными функ-

циями:

W (s) = k/(Ts — 1); W (s) = к (Ts — I); W (s) - kf(T*s

—

—2ITs + 1); W(s) = k (TV —

2%Ts

+ 1)

и др. Для неминимально-фазового звена характерно, что

у него сдвиг фазы по модулю больше, чем у минимально-фазо-

вого звена, имеющего одинаковую с неминимально-фазовым

звеном АЧХ.

На рис. 2.11 приведены ЛЧХ неминимально-фазовых

звеньев с передаточными функциями W (s) = 1 /(Ts — 1) (рнс.

2.11, а) и W (s) к (Ts — 1) (рис. 2.11, б). ЛАЧХ этих звень-

ев совпадают с ЛАЧХ апериодического (см. рис. 2.7, б) и фор-

сирующего (см. рис. 2.8, б) звеньев. Сдвиг фазы у последних

меньше: фазовые частотные функции апериодического и форси-

рующего звеньев по абсолютной величине не превышают зна-

чения л/2, а фазовые частотные функции соответствующих не-

минимально-фазовых звеньев достигают по абсолютной вели-

чине значения я. К неминимально-фазовым звеньям относят

также звено чистого запаздывания с передаточной функцией

W (s) =

Частотная передаточная функция

W (/со) = к (cos

сот

— / sin сот).

Для остальных частотных н временных функций имеем:

(со)

= fe cos сот; V (со) = — k sm сот; А (со) = k\

(

) = —

шт;

20 lg k; h (t) = ftl (* — T); w (t) =

= £6 (* — x).

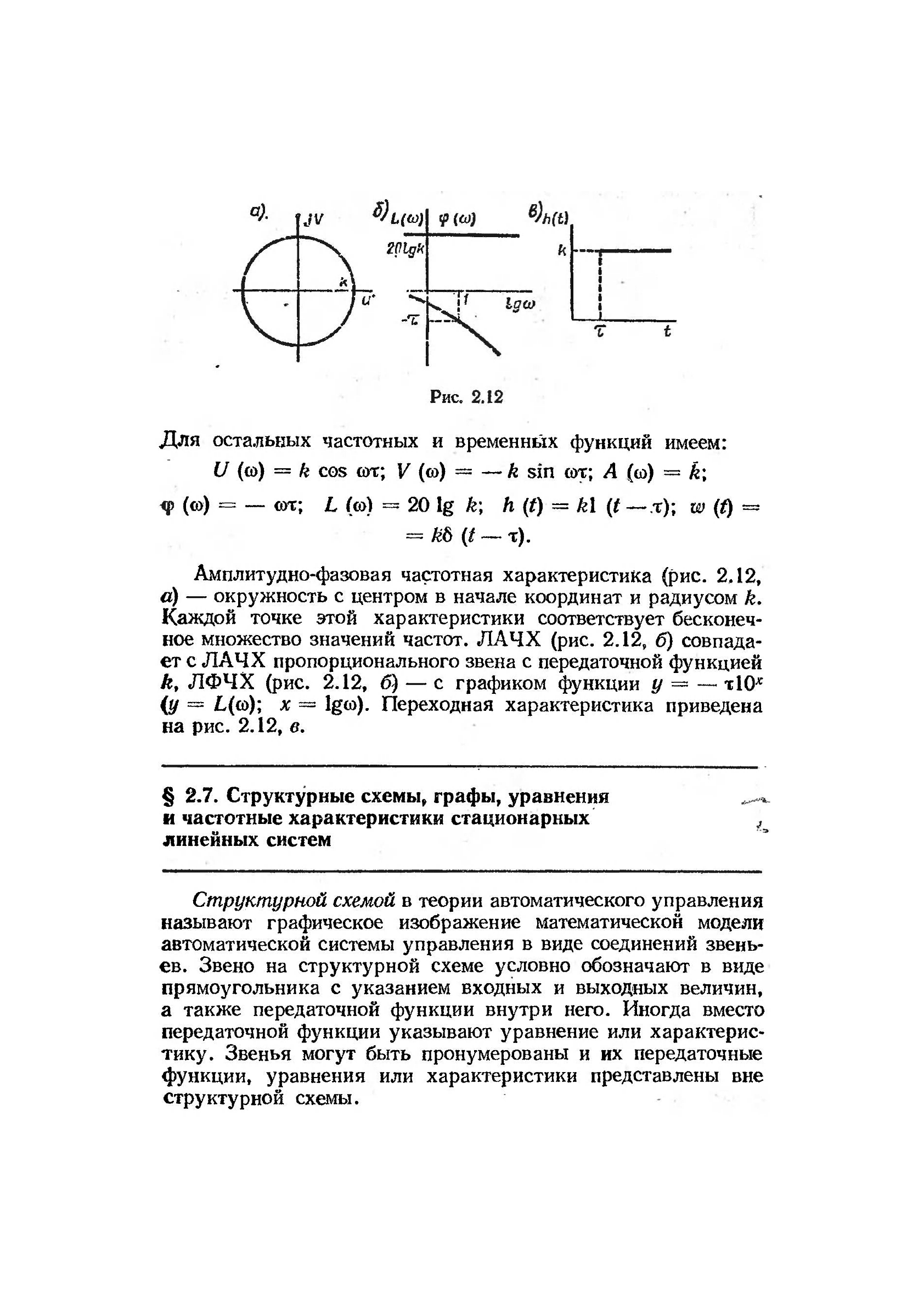
Амплитудно-фазовая частотная характеристика (рис. 2Л2,

а) — окружность с центром в начале координат и радиусом k.

Каждой точке этой характеристики соответствует бесконеч-

ное множество значений частот. ЛАЧХ (рис. 2.12, б) совпада-

ет с ЛАЧХ пропорционального звена с передаточной функцией

А, ЛФЧХ (рис. 2.12, б) — с графиком функции у = — т10*

{у = L(со); х = Igco). Переходная характеристика приведена

на рис. 2.12, в.

§ 2.7. Структурные схемы, графы, уравнения

и частотные характеристики стационарных

линейных систем

Структурной схемой в теории автоматического управления

называют графическое изображение математической модели

автоматической системы управления в виде соединений звень-

ев. Звено на структурной схеме условно обозначают в виде

прямоугольника с указанием входных и выходных величин,

а также передаточной функции внутри него. Иногда вместо

передаточной функции указывают уравнение или характерис-

тику. Звенья могут быть пронумерованы и их передаточные

функции, уравнения или характеристики представлены вне

структурной схемы.

Входные и выходные величины записывают в виде изобра-

жений, если передаточные функции задают в форме изображе-

ний. Если же передаточные функции задают в операторной

форме или звенья описывают дифференциальными уравнения-

ми, то входные и выходные переменные записывают в виде ори-

гинала.

Сравнивающие (рис. 2.13, а, б) и суммирующие (рис. 2.13,в)

звенья изображают в виде круга, разделенного на секторы.

В сравнивающем звене сектор, на который подается «вычитае-

мое», затемняют (рис. 2.13, б) или перед соответствующим вхо-

дом ставят знак минус (рис. 2.13, а).

Структурную схему широко используют на практике при

исследовании и проектировании автоматических систем управ-

ления, так как она дает наглядное представление о связях

между звеньями, о прохождении и преобразовании сигналов в

системе.

При математическом описании автоматическую систему

обычно изображают в виде блок-схемы и для каждого «блока»

(элемента) записывают уравнения, исходя из физических за-

конов, которым подчиняются процессы в нем. Структурную

схему можно составить на основании этой блок-схемы и полу-

ченных уравнений или только на основании последних. И даль-

нейшие преобразования, необходимые для получения уравне-

ний и передаточных функций системы, проще и нагляднее про-

изводить по структурной схеме.

Звено на структурной схеме не обязательно изображает

модель какого-либо отдельного элемента. Оно может быть мо-

делью элемента, соединения элементов или вообще любой час-

ти системы.

Основные правила лреобразования структурных схем.

1. Последовательное соединение звеньев (рис. 2.14, а). При

последовательном соединении выходная величина каждого

предшествующего звена является входным воздействием по-

следующего звена. При преобразовании структурных схем це-

почку из последовательно соединенных звеньев можно заме-

нить одним звеном (рис.

2.14, б) с передаточной

а) в)

функцией W (s)

равной V /Оч^г gf/O^W? tt/Оч^Ц+%

произведению передаточ-

ных функций отдельных

звеньев:

(s)=П W

fa).

i=i

Рис. 2.13

Рис. 2.14

- *

Запишем уравнения звеньев у

= W

..., у

- W

!/n~i-

Исключив из этой системы переменные у

...,

получим

Уп =W

W»..

откуда

П U7

г г

2. Параллельное соединение звеньев (рис. 2.15, а). При па-

раллельном соединении на вход всех звеньев подается один и

тот же сигнал, а выходные величины складываются. Цепь из

параллельно соединенных звеньев можно заменить одним

звеном (рис. 2.15, б) с передаточной функцией W (s), равной

сумме передаточных функций входящих в нее звеньев: IV (s)^=

= 2 ^ (

)- Для вывода этой формулы составим уравнения

i = I

для каждых звеньев:

У1

= Wjtfoi у

= W

\ ...; у

= №

Сложив эти уравнения и учитывая, что у = 2 получим

i = 1

искомую формулу.

3. Звено, охваченное обратной

связью

(рис. 2.16, а). При-

нято считать, что звено охвачено обратной связью, если его

выходной сигнал через какое-либо другое звено подается на

вход. При этом если сигнал у

обратной связи вычитается

из входного воздействия у

, т. е. е

= у

— у

то обратную

связь называют отрицательной. Если сигнал у± обратной свя-

зи складывается с входным воздействием у

, т. е. е

= у

+ у

то обратную связь называют положительной.

Разомкнем обратную связь перед сравнивающим звеном

(рис. 2.16, а). Тогда получим цепь из двух последовательно

соединенных звеньев. Поэтому передаточная функция W разом-

кнутой цепи (рис. 2.16, а) равна произведению передаточной

функции W

прямой цепи и передаточной функции W

Q с

об-

ратной связи: W = W

W О-С (рис. 2.16, б).

Передаточная функция \F

замкнутой цепи с отрицатель-

ной обратной связью — звена, охваченного отрицательной об-

ратной связью, — равна передаточной функции прямой цепи,

деленной на единицу плюс передаточная функция разомкну-

той цепи:

W, - WJ{\ + W).

Для вывода этой формулы выпишем уравнения для каждого

звена:

yt^W

В этой системе последнее уравнение — уравнение сравнива-

ющего звена — называют уравнением замыкания.

Исключив переменные е

и у

из приведенной системы, по-

лучим уравнение у = W

(у

— W

y) или (1 + W

)y=

. Отсюда

- WJ(\ + W

J - WJ{

+ W).

Если обратная связь положительна, то аналогично полу-

чим W

- W

/( 1 — IF).

Передаточная функция замкнутой цепи с положительной

обратной связью равна передаточной функции прямой цепи,

а)

Рис. 2.15 Рее. 2.16

деленной на единицу минус передаточная функция разомкну-

той цепи. Если передаточная функция

QwC

= 1, то обратная

связь называется единичной и структурная схема изображает-

ся так, как показано на рис. 2.16, е. Передаточная функция

при этом принимает вид W

== W

/( 1 + W

) при отрица-

тельной обратной связи и W

— W

)( 1 — W

) при положи-

тельной обратной связи.

При преобразовании структурных схем возникает необхо-

димость переноса и перестановки сумматоров и узлов. Рас-

смотрим, какие изменения в схеме при этом нужно произвести.

4. Перенос сумматора (рис. 2.17). Легко показать, что при

переносе сумматора по ходу сигнала необходимо добавить зве-

но с передаточной функцией, равной передаточной функции

звена, через которое переносится сумматор (рис. 2.17, а). Если

сумматор переносится против хода сигнала, то необходимо до-

бавить звено с передаточной функцией, равной обратной пере-

даточной функции звена, через которое переносится сумматор

(рис. 2.17, б).

При переносе сумматора возникают неэквивалентные уча-

стки линии связи. Эти участки на рис. 2.17 заштрихованы.

5. Перенос узла (рис. 2.18, а). При переносе узла также не-

обходимо добавить звено. Если узел переносится по ходу сиг-

нала, то добавляется звено с передаточной функцией, равной

обратной передаточной функции звена, через которое перено-

сится узел (рис. 2.18, б). Если узел переносится против хода

сигнала, то добавляется звено с передаточной функцией, рав-

ной передаточной функции звена, через которое переносится

узел (рис. 2.18, в).

а)

(

у 2

Рис. 2.17