Воронов А.А. Теория автоматического управления. Часть первая

Подождите немного. Документ загружается.

фективность во время переходного про-

цесса между отдачей команды и получе-

нием окончательного результата. Объяс-

няется это тем, что обычно в таких си-

стемах потери в переходном процессе

достаточно малы и влияют несуществен-

но на общую величину выигрыша в уста-

новившемся режиме, поскольку сам уста-

новившийся режим значительно более

длителен, чем переходный процесс. Но

иногда динамика не исследуется из-за математических труд-

ностей. Методам оптимизации конечных состояний в орга-

низационных и экономических системах посвящены курсы

методов. оптимизации и исследования операций.

В управлении динамическими техническими системами

оптимизация часто существенна именно для переходных про-

цессов, в которых показатель эффективности зависит не толь-

ко от текущих значений координат (как в экстремальном уп-

равлении), но и от характера изменения в прошлом, настоящем

и будущем, и выражается некоторым функционалом от коор-

динат, их производных и, может быть, времени.

В качестве примера можно привести управление бегом спортсме-

на на дистанции. Так как его запас энергии ограничен физиологиче-

скими факторами, а расходование запаса зависит от характера бега,

спортсмен уже ие может в каждый момент отдавать максимум возмож-

ной мощности, чтобы не израсходовать запас энергии преждевременно

и ие выдохнуться иа дистанции, а должен искать оптимальный для

своих особенностей режим бега.

Нахождение оптимального управления в подобных динами-

ческих задачах требует решения в процессе управления доста-

точно сложной математической задачи методами вариацион-

ного исчисления или математического программирования "в

зависимости от вида математического описания (математиче-

ской модели) системы. Таким образом, органической состав-

ной частью системы оптимального управления становится

счетно-решающее устройство или вычислительная машина.

Принцип поясняется на рис. 1.10. На вход вычислительного

устройства (машины) ВМ поступает информация о текущих

значениях координат х с выхода объекта О, об управлениях и

с его входа, о внешних воздействиях z на объект, а также за-

дание извне различных условий: значение критерия оптималь-

ности J, граничных условий х (0), х (оо ), информация о до-

пустимых значениях x^Xuu^Vht. П. Вычислительное

Рис. 1.10

устройство по заложенной в него программе вычисляет опти-

мальное управление и. Оптимальные системы могут быть как

разомкнутыми, так и замкнутыми.

Адаптивные системы. В реальных условиях внешние воз-

мущения иногда приводят к изменению не только координат,

но и параметров системы (коэффициентов уравнений), причем

в таких системах, как баллистические ракеты, изменения па-

раметров существенны. Изменения параметров, вышедшие

за определенные границы, приводят не только к количествен-

ным ошибкам или к ухудшению других показателей качества

системы, но зачастую и к полной потере ее работоспособности.

Эти потери качества часто невозможно устранить, находясь

в рамках первоначально принятого фундаментального принци-

па управления, это можно сделать лишь путем изменения па-

раметров (а иногда и структуры) системы так, чтобы приблизить

математическое описание претерпевшей изменения системы к

ее исходной модели настолько, чтобы сохранить работоспо-

собность первоначально принятого фундаментального прин-

ципа управления.

Системы, автоматически изменяющие значение своих па-

раметров или структур при непредвиденных изменениях внеш-

них условий на основании анализа состояния или поведения

системы так, чтобы сохранялось заданное качество ее работы,

называют адаптивными системами (от лат. adaptio — при-

способление). Термин заимствован из биологии, где адаптаци-

ей называют приспособление организма к изменяющейся среде

с целью сохранения жизнедеятельности. Но в теории управле-

ния (так как любая автоматическая система в каком-то смысле

приспосабливается к изменениям среды) понятие адаптации

умышленно сужено: к ней относят лишь такие виды приспо-

собления, которые осуществляются путем изменения уп-

равляющим устройством параметров или структуры системы

по данным анализа ее работы.

Адаптивные системы с изменением значений параметров

иногда "называют самонастраивающимися, а системы с измене-

нием структуры и алгоритма управления — самоорганизую-

щимися.

Обычно адаптивная система содержит в качестве «ядра» схе-

му, реализующую один из фундаментальных принципов управ-

ления, а контур адаптации пристраивают к ней как вторич-

ный, осуществляющий коррекцию параметров. Контур адап-

тации, обычно состоящий из устройства измерения ИУ, вы-

числения ВУ и управления УУ, может быть разомкнут

а)

ИУ

ВУ

УУ

6М1

-<8н

б)

ИУ

ВУ

УУ бНП

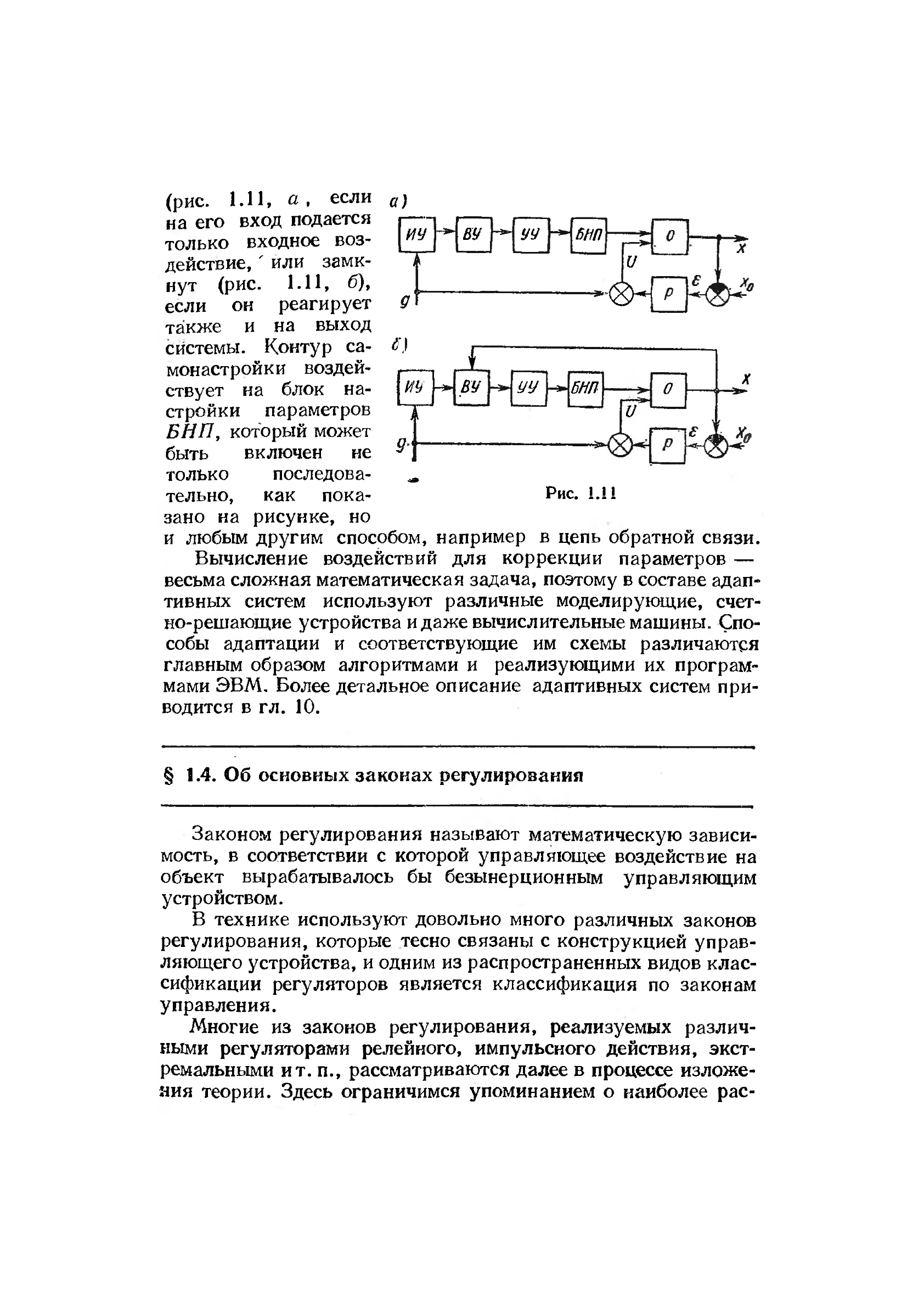
(рис. i.ll, а), если

на его вход подается

только входное воз-

действие, ' или замк-

нут (рис. 1.11, б),

если он реагирует

также и на выход

системы. Контур са-

монастройки воздей-

ствует на блок на-

стройки параметров

БНП, который может

быть включен не

только последова-

тельно, как пока-

зано на рисунке, но

и любым другим способом, например в цепь обратной связи.

Вычисление воздействий для коррекции параметров —

весьма сложная математическая задача, поэтому в составе адап-

тивных систем используют различные моделирующие, счет-

но-решающие устройства

даже вычислительные машины. Спо-

собы адаптации и соответствующие им схемы различаются

главным образом алгоритмами и реализующими их програм-

мами ЭВМ. Более детальное описание адаптивных систем при-

водится в гл. 10.

-а»

Рис. 1.11

§ 1.4. Об основных законах регулирования

Законом регулирования называют математическую зависи-

мость, в соответствии с которой управляющее воздействие на

объект вырабатывалось бы безынерционным управляющим

устройством.

В технике используют довольно много различных законов

регулирования, которые тесно связаны с конструкцией управ-

ляющего устройства, и одним из распространенных видов клас-

сификации регуляторов является классификация по законам

управления.

Многие из законов регулирования, реализуемых различ-

ными регуляторами релейного, импульсного действия, экст-

ремальными ит. п., рассматриваются далее в процессе изложе-

ния теории. Здесь ограничимся упоминанием о наиболее рас-

пространенных законах, реализуемых линейными регулятора-

ми по отклонению непрерывного действия. В этих простей-

ших законах управляющее воздействие линейно зависит от

отклонения, его интеграла и первой производной по време-

ни. При описании законов наиболее удобно использовать без-

размерные относительные переменные е = |jt = и/и§,

где х

и и

— базовые значения (например, соответствующие

номинальному режиму объекта).

Пропорциональный закон (обозначаемый П): \i = &

е.

Регулятор, осуществляющий этот закон, называют пропор-

циональным. Постоянную k

называют

коэффициентом

переда-

чи (усиления) регулятора, обратную величину

—

статизмом

регулятора. С возрастанием статизма регулятора возрастает и

статизм регулирования. Интегральный закон (И):

[х

= -

edt или d\i/dt = е/7\

Постоянная Т имеет размерность времени, и ее называют

постоянной времени интегрирования. Интегральный регуля-

тор — астатический, и именно с его помощью осуществляется

рассмотренная выше простейшая схема астатического регу-

лирования. Пропорционально-интегральный закон (ПИ):

^ = +

Иногда его называют пропорциональным законом с интег-

ральной коррекцией. Регулятор ПИ также обеспечивает аста-

тическое регулирование. В этом можно убедиться, представив

уравнение в виде d\x/dt — k

(de/dt + в/Г).

В состоянии равновесия при постоянных воздействиях

должно быть d[i/dt = 0; de/dt = 0, откуда равновесие может

иметь место лишь при в = 0. Пропорционально-интегрально-

дифференциальный закон (ПИД):

(

I С de

e + -J еЛ + 7„

Постоянные Т

и Т

соответственно называют постоянны-

ми времени интегрирования и дифференцирования. Регулятор

ПИД так же обеспечивает астатическое регулирование. Про-

изводную de/dt вводят в закон регулирования для повышения

качества процесса регулирования.

Глава 2

МАТЕМАТИЧЕСКОЕ

ОПИСАНИЕ

АВТОМАТИЧЕСКИХ

СИСТЕМ УПРАВЛЕНИЯ

§ 2.1. Уравнения динамики и статики.

Линеаризация

На определенном этапе разработки

и исследования автоматической систе-

мы управления получают ее математи-

ческое описание

—

описание процессов,

проистекающих в системе, на языке ма-

тематики. Математическое описание мо-

жет быть аналитическим (с помощью

уравнений), графическим (с помощью

графиков, структурных схем и графов) и

табличным (с помощью таблиц).

Для получения математического опи-

сания системы обычно составляют опи-

сание ее отдельных элементов. В част-

ности, для получения уравнений систе-

мы составляют уравнения для каждого

входящего в нее элемента. Совокупность

всех уравнений элементов и дает урав-

нения системы.

Уравнения (а также структурные схе-

мы) автоматической системы управле-

ния называют ее математической мо-

делью. Такое название обусловлено тем,

что при математическом описании (сос-

тавлении уравнений) физических про-

цессов всегда делают какие-либо допу-

щения и приближения. Математическая

модель одной и той же системы в зави-

симости от цели исследования может

быть разной. Более того, иногда полез-

но при решении одной и той же задачи

на разных этапах принимать разную ма-

тематическую модель: начать исследова-

ние с простейшей модели, а затем ее по-

степенно усложнять, с тем чтобы учесть

дополнительные явления и связи, кото-

рые на начальном этапе были отброшены

как несущественные. Сказанное обуслов-

ливается тем, что к математической мо-

дели предъявляются противоречивые тре-

Рис. 2.1 бования: она должна, с одной стороны,

как можно полнее отражать свойства ори-

гинала, а с другой стороны, быть по возможности простой,

чтобы не усложнять исследование.

Система управления и любой ее элемент производят преоб-

разование входного сигнала х (Q в выходной сигнал у (t).

С математической точки зрения они осуществляют отображение

у (t) - Ах

<*),

согласно которому каждому элементу х (t) из множества X

входных сигналов (х (0 £ X) ставится в соответствие единст-

венный, вполне определенный элемент у (0 из множества Y вы-

ходных сигналов [у (/) £ Y1. В приведенном соотношении А

называется оператором. Оператор, определяющий соответст-

вие между входным и выходным сигналами системы управле-

ния (элемента), называется оператором этой системы (эле-

мента). Задать оператор системы — это значит задать правило

определения выходного сигнала этой системы по ее входному

сигналу.

Рассмотрим математическое описание непрерывных систем

управления с помощью дифференциальных уравнений. В боль-

шинстве случаев звенья и системы описываются нелинейными

дифференциальными уравнениями произвольного порядка.

Здесь под звеном понимается математическая модель элемен-

та. Для примера рассмотрим звено (рис. 2.1), которое можно

описать дифференциальным уравнением второго порядка

F(y,y,y,u

d) + f~

О,

(2.1)

где у — выходная величина; и и f — входные величины; у

* ..

и и — первые производные по времени; у — вторая производ-

ная по времени.

Уравнение (2.1), описывающее процессы в звене при про-

извольных входных воздействиях, называют уравнением ди-

намики. Пусть при постоянных входных величинах и =

и / = /

процесс в звене с течением времени установится:

выходная величина примет постоянное значение у = Тог-

да (2.1) примет вид

(2.2)

Это уравнение описывает статический или установившийся

режим и его называют уравнением статики.

Статический режим можно описать графически с помощью

статических характеристик. Статической характеристикой

звена или элемента (а также системы) называют зависимость

выходной величины от входной в статическом режиме. Стати-

ческую характеристику можно построить экспериментально,

подавая на вход Элемента постоянное воздействие и измеряя

выходную величину после окончания переходного процесса,

или расчетным путем, используя уравнение статики.

Если звено имеет несколько входов, то оно описывается с

помощью семейства или семейств статических характеристик.

Например, звено, характеризующееся в статическом режиме

уравнением (2.2), можно описать графически с помощью семей-

ства статических характеристик, представляющих собой кри-

вые зависимости выходной величины у от одной входной вели-

чины и (или /) при различных фиксированных значениях дру-

гой — f (или и).

Линеаризация. Обычно автоматические системы описыва-

ют нелинейными дифференциальными уравнениями. Но во

многих случаях можно их линеаризовать, т. е. заменить ис-

ходные нелинейные уравнения линейными, приближенно

описывающими процессы в системе. Процесс преобразования

нелинейных уравнении в линейные называют линеаризацией.

В атоматических системах должен поддерживаться неко-

торый заданный режим. При этом режиме входные и выходные

величины звеньев системы изменяются по определенному зако-

ну. В частности, в системах стабилизации они принимают оп-

ределенные постоянньш значения. Но из-за различных возму-

щающих факторов фактический режим отличается от тре-

буемого (заданного), поэтому текущие значения входных и вы-

ходных величин не равны значениям, соответствующим задан-

ному режиму. В нормально функционирующей автоматической

системе фактический режим немного отличается от требуемого

режима и отклонения входных и выходных величин входящих

в нее звеньев от требуемых значений малы. Это позволяет про-

извести линеаризацию, разлагая нелинейные функции, вхо-

дящие в уравнения, в ряд Тейлора. Линеаризацию можно

производить по звеньям.

Пример 2.1. Проиллюстрируем изложенное на примере звена,

описываемого уравнением (2.1). Пусть заданному режиму соответст-

вуют

и~=и*;

«*;

/ = у=у*\ у=у*; у=у*. (2.3)

Обозначим отклонения реальных значений «, / и у от требуемых

через Аи, Д/ и Ду, т. е. Аи •= и — и*, Д/ = / — /*, ~ у — у*.

Тогда и == и* + Да; и

===

и* + Ди; / = f* + А/; р = у* + А^/; у =

= у* + А#; у = if* -}- Ду. Подставим эти выражения в (2.1) и, рас-

сматривая Z

как функцию от независимых переменных и, и, у, у и у\

разложим ее в ряд Тейлора в точке (2.3) и отбросим малые члены бо-

лее высокого порядка, чем отклонения. Тогда (2.1) примет вид

F* + (dFIdy)* Ау+ (dFjdij)

Ay+(dF/dy)* Aу+ (dF/du)* Au +

+ (dF fdu) * Au + f* + А/ = 0. (2.4)

Здесь звездочка сверху обозначает, что соответствующие функ-

ции и производные вычисляются при значениях аргумента, определяе-

мых соотношениями (2.3). Когда в системе устанавливается заданный

режим, уравнение (2.1) принимает вид F* + /* = 0. Вычтя это урав*

ние из (2.4), получим искомое уравнение звена в отклонениях:

«V «

-f-

Ау-\-а

А у—b

А и

—

—с

А[

= 0, (2.5)

где a^(dF/dy)*\ а

=*(дР/ду)*1 a

^(dF/dy)*;

= — (dF/du)*; — (dF/du)*; с

~ — I»

Если время t явно не входит в исходное уравнение (2.1) и, кроме

того, заданный режим является статическим — величины у*, и* и /*

ие зависят от времени, то коэффициенты линеаризованного уравнения

(2.5) являются постоянными.

Звенья и системы, которые описываются линейными урав-

нениями, называют соответственно линейными звеньями и ли-

нейными системами.

Уравнение (2.5) было получено при следующих предполо-

жениях: 1) отклонения выходной А у и входной А и величин до-

статочно малы; 2) функция F обладает непрерывными частны-

ми производными по всем своим аргументам в окрестности то-

чек, соответствующих заданному режиму. Если хотя бы одно

из этих условий не выполняется, то линеаризацию произво-

дить нельзя. По поводу первого условия необходимо отметить

следующее: нельзя раз и навсегда установить, какие отклоне-

ния считать малыми. Это зависит от вида нелинейности.

Часто нелинейную зависимость между отдельными пере-

менными, входящими в уравнение звена, задают в виде кри-

вой. В этих случаях линеаризацию можно произвести графи-

чески.

Геометрически линеаризация

нелинейной зависимости между

двумя переменными (рис. 2.2) озна-

чает замену исходной кривой АВ

отрезком ее касательной А'В' в

точке 0\ соответствующей задан-

ному режиму, и параллельный

перенос начала координат в эту

точку.

В зависимости от того, вхо-

дит или нет время явно в урав- Рис. 2.2

нение, системы разделяют на

стационарные и нестационарные.

Автоматические системы управления (звенья) называют

стационарными, если они при постоянных внешних воздейст-

виях описываются уравнениями, не зависящими явно от време-

ни. Это означает, что свойства системы со временем не изменя-

ются. В противном случае система называется нестационар-

ной. Для линейных систем можно дать также следующее опре-

деление: стационарными линейными системами (звеньями)

называют системы (звенья), которые описываются линейными

уравнениями с постоянными коэффициентами; нестационарны-

ми линейными системами (звеньями) или системами с пере-

менными параметрами — системы (звейья), которые описы-

ваются линейными уравнениями с переменными коэффици-

ентами.

§ 2.2. Основные свойства преобразования Лапласа

В этом параграфе даны основные сведения о преобразова-

нии Лапласа, которые будут использованы при рассмотрении

систем, описываемых линейными дифференциальными уравне-

ниями.

Преобразованием Лапласа называют соотношение

X(s)= J

л: 0

)e-

ставящее функции х {t) вещественного переменного в соответ-

ствие функцию X (s) комплексного переменного s (s = а+

+/о>). При этом х (f) называют оригиналома X (s) — изобра-

жением или изображением по Лапласу. То, что х (/) имеет сво-

им изображением X (s) или оригиналом X (s) является х (£),

записывается так:

х (t) ф X (s) или X ($) Ф х (t).

Иногда также пользуются символической записью

X (s) - L {х (0>,

где L — оператор Лапласа.

Предполагается, что функция х (t), которая подвергается

преобразованию Лапласа, обладает следующими свойствами:

X (0 определена и кусочно-дифференцируема на всей положи-

тельной числовой полуоси [0, оо]; х (t) =

при t < 0; суще-

ствуют такие положительные числа Ж и с, что \х (£)| ^ Me

при 0 ^ t < оо. Функции, обладающие указанными тремя

свойствами, часто называют функциями-оригиналами.

Соотношение

/оо

х (0 - ~ j х (s)

est

dSj

(Уо

—

определяющее по известному изображению его оригинал

(в

точ-

ках непрерывности последнего), называют обратным преобра-

зованием Лапласа. В нем интеграл берется вдоль любой пря-

мой Res — о

> с. Символически обратное преобразование

Лапласа можно записать так:

где символ L"

— обратный оператор Лапласа.

Остановимся на основных свойствах преобразования Лап-

ласа.

1. Свойство линейности. Для любых постоянных аир

L {ax

(t) + P*

(t)} - aL (t)} + PL {*

(t)}.

2. Дифференцирование оригинала. Если производная х (t)

является функцией-оригиналом, т. е. обладает указанными вы-

ше тремя свойствами, то L {х (t)} = sX (s) — х (0), где

<п)

X(s) = L {х (£)}, я(0) = Нш х (t). Если n-я производная х (t)

является функцией-оригиналом, то

L \ х(t)) =s

X(s) —s

x(0)—s"~

x(0)—.,.—x (0),

(k)

где я(0) =Нша: (t), = —1.