Воронов А.А. Теория автоматического управления. Часть первая

Подождите немного. Документ загружается.

Рассмотрим случай вещественных корней характеристиче-

ского уравнения (6.55). Вещественные корни получаются при

g = 1. Тогда s = т—о. В этом случае параметры щ и р

свя-

заны одним уравнением

А (со) щ + В (со) щ + С (со) 0, (6.72)

где

п п

I tч

Л = 2 «П-*G

(to); В= 2 Pn-fcG

(o>);

С- 2 (©); sG

fa) = I)****.

fe=0

(6.72а)

Для определения G/,., i («О

вспользуёТбя рекуррентная

формула

(ft+1)

—e>G

.(to)i k—0, 1,2;;.;.

•

s- ..

<ч

- •.| : -: r:

При ЭТОМ Go (w) = 1. . .

В'плоскости параметров и

при каждом значении,

со

урав-

ние (6.72) определяет прямую. Это особые прямые.

Если строится область устойчивости,, то определяются две

прямые, соответствующие корню, находящемуся в бесконеч-

ности, и корню, расположенному в начале координат. Если

строится область с заданной степенью устойчивости Г|, то бе-

рется корень, расположенный в точке [—tj, 01. Особые прямые

совпадают с прямыми в традиционном методе £>-разбиения и

определяются аналогично.

Найдем область параметров щ и соответствующую чи-

сто мнимым корням характеристического уравнения.

Чисто мнимые корни уравнения (6.55) исходя из (6.62а)

получаются при £ = 0. При этом s = /со. При £ = 0 рекур-

рентная формула принимает вид (6.68):

при Qo (со, 0) = 1; Qx (со, 0) - 0.

Отсюда следует, что

0)2

Q2h-2i

(6.73)

Они-

и. следовательно, формулы для коэффициентов (6.71), опреде-

ляющих систему (6.64), принимают вид

А.

= Ai (со, 0) =

1 2 J

= 2 ««

fc=o

Г—]

—2fe Q*k (<*>,

(<0,0).

1 2 ]

= S Рг

f—1

i~2h

(*>,

0);

Сг

= С

(о),0) =

I. 2 j

S Уп-

к— 0

-2

Qth

(©. 0);

А =

А (ю, 0) =

]

1 2 j

fe— 0

Qtk (*>, 0);

(с>,0)==

[ 2 j

2 Р»-

n—11

i Q*k (w, 0);

(«.0) =

. 2 j

2 vn-

-2Л-1 Qafe

(6.74)

Функции Q

(со, 0) вычисляются по рекуррентной формуле

(6.73) при

(со, 0) = I.

Параметры fx

и (х

для каждого значения со, при котором

ЪгВъ—АъШгф 0,

вычисляются по формулам

—С г В

2 ф

—С

—

—* \h~zrz

At B

—Az B

—i4

(6J5)

Полученные соотношения могут быть применены для построе

ния областей на плоскости параметров исходя из условия

расположения корней характеристического уравнения внутри

угла, трапеции, полукруга или исходя из заданной степени

устойчивости. Например, при построении области изменения

параметров и ц

исходя из расположения корней характери-

ческого уравнения внутри угла 2<р в левой полуплоскости

(рис. 6.7, а) используются формулы (6.65а) и (6.71). При по-

строении областей изменения параметров с учетом заданной сте-

пени устойчивости (рис. 6.7, б) используются формулы, полу-

ченные для случая вещественных отрицательных корней харак-

теристического уравнения, т. е. в формулы (6.65а) подстав-

ляются формулы (6.72а).

Пример 6.6. Рассмотрим характеристическое уравнение замкну-

той системы

ао s

-+-

+а

-f а

s-fа

= 0.

Коэффициенты характеристического уравнения зависят от двух па-

раметров fij и [х

линейно:

= + +

* —

1,2,3,4.

и имеют вид а

= 0,04 щ; а

= 0,36 щ + 0,04; a

= -+- 0,36;

— -f 0,4щ + 2; a

= 2щ + 2.

Необходимо найти значения параметров щ и ДЛЯ которых ха-

рактеристическое уравнение имеет корни, расположенные слева от

мнимой оси внутри угла

<р

= 60° (§ = 0,5). Запишем коэффициенты ха-

рактеристического уравнения следующим образом:

Обо = 0,04; Ро = 0; Vo = 0; = 0,36; = 0; у* = 0,04; а

-2;

Ра - 0; у^ = 0,36; 2; = 0,4; 2; а

= 0; р

=2; =

Определим функции Q

для каждого значения со по рекур-

рентной формуле

<?*+!*= —ЯюбОл—1; —авйЕ).

Для | = 0,5 имеем Q

= 1; Qi = — <о (Л = 4).

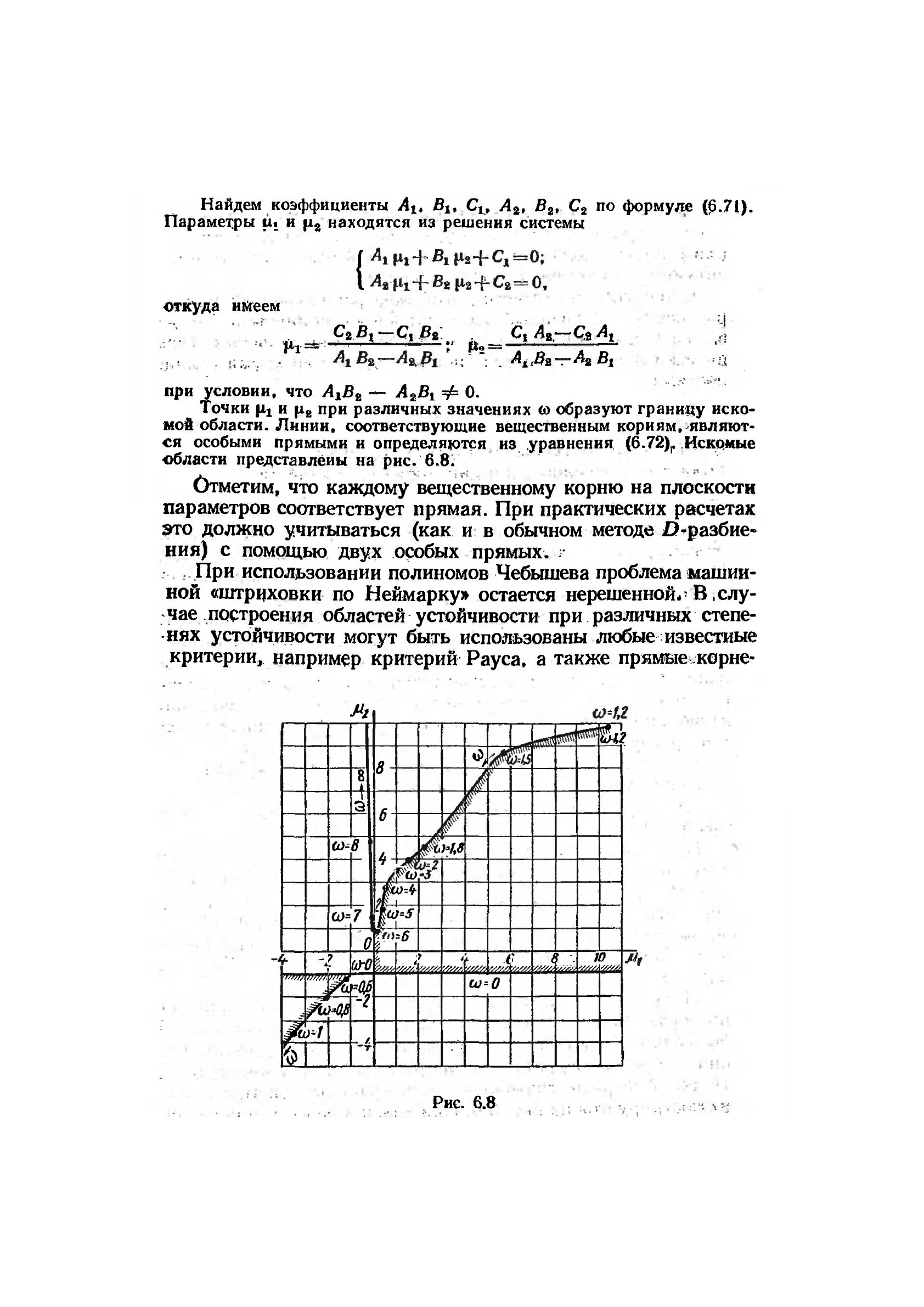
Найдем коэффициенты A

, В

, С

по формуле (£.71).

Параметры и fi

находятся из решения системы

{

откуда ийгеем

С 2В

—С

—С А А

• • '

•—

До — —

;

— -

: A

d^A

при условии, что А

— A

Ф 0.

Точки I*! и fx

при различных значениях <о образуют границу иско-

мой области. Линии, соответствующие вещественным кори ям, являют-

ся особыми прямыми и определяются из уравнения (6.72)^. Искомые

области представлены на рис. 6.8.

Отметим, что каждому вещественному корню на плоскости

параметров соответствует прямая. При практических расчетах

это должно учитываться (как и в обычном методе D-разбие-

ния) с помощью двух особых прямых,

При использовании полиномов Чебышева проблема машин-

ной «штриховки по Неймарку» остается нерешенной,

В .слу-

чае построения областей устойчивости при различных степе-

нях устойчивости могут быть использованы любые известные

критерии, например критерий Рауса, а также прямые корне-

Ы2

О 4

СО-

fio

fw-b

С0=

fW-S

& 1

CQ-0

ш*

'////Л

шл

f .

ША

'Г'Г/Т;

7Ш.

щЛ

гЩ

cv=

)*QJ&

-1

)-1

_ /

• •

Рис. 6.8

вые методы. При построении области исходя из расположения

корней характеристического уравнения внутри угла, трапеции

или в других областях слева от мнимой оси корневые методы

являются единственно эффективными.

В заключение отметим, что модифицированный метод D-

разбиения, основанный на применении полиномов Чебыше-

ва, дает возможность вести исследование импульсных, гармо-

нически линеаризованных систем с одной или двумя нелиней-

ностями.

« - "" I '

*"«

' I

•* .

•

г ' •

•

' •

•

•• "

" — . • . .•.••'•'••»•• • • ' • . . . • • I

•

§ 6.11. Универсальные методы построения

областей устойчивости и динамического качества

. ...

:; Если каким-либо образом найдена первая точка границы

области, можно обойти весь контур, двигаясь вдоЛь границы.

Наиболее простой способ слежения состоит в использовании

принципа взаимно-перпендикулярной ориентации.

Пусть построение границы искомой области происходит в

двумерном пространстве, т. е. на плоскости. Алгоритй движе-

ния вдоль границы состоит в следующем. Направлениё изме-

нения параметров на плоскости параметров и |х

осущест-

вляется в четырех возможных направлениях: вверх, вниз,

влево, вправо, т. е. по сторонам квадрата. В вершинах квадра-

тов проверяется выполнение условия G (fi

) I-

Если на данном шаге изменения параметров мы пересека-

ем границу и попадаем в искомую область, то G (щ, fx

) <С /.

В этом случае следующий шаг выполняется с поворотом по ча-

совой стрелке.

Если на очередном шаге изменения параметров мы пересе-

каем границу и выходим из искомой области, то G (fi

щ) >

;> /. В этом случае следующий шаг изменения параметров вы-

бирается таким образом, чтобы движение происходило с пово-

ротом против часовой стрелки. Легко видеть, что граница об-

ласти находится в точке, где соблюдается условие G (fjb

) =

Получение более точного положения точки границы мож-

но осуществить, применяя метод деления интервала, так, что-

бы границы строились по точкам на расстоянии, равном поло-

вине стороны квадрата, или на расстояния, равном одной тре-

ти ее. Алгоритм движения вдоль границы искомой области

иллюстрируется на рис. 6.9. При каждом пересечении границы

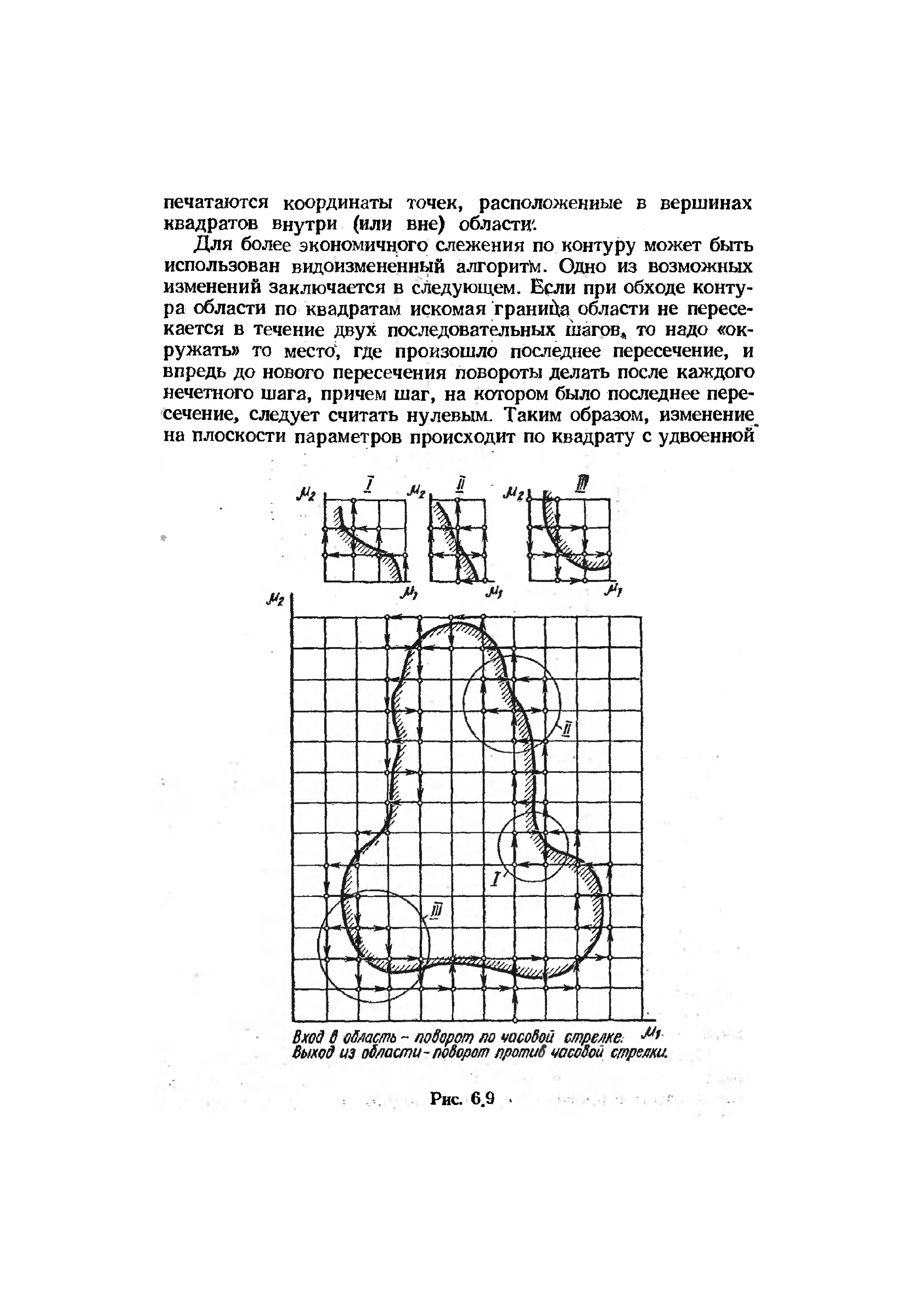
печатаются координаты точек, расположенные в вершинах

квадратов внутри (или вне) области'.

Для более экономичного слежения по контуру может быть

использован видоизмененный алгоритм. Одно из возможных

изменений заключается в следующем. Если при обходе конту-

ра области по квадратам искомая граница области не пересе-

кается в течение двух последовательных шагов* то надо «ок-

ружать» то место; где произошло последнее пересечение, и

впредь до нового пересечения повороты делать после каждого

нечетного шага, причем шаг, на котором было последнее пере-

сечение, следует считать нулевым. Таким образом, изменение^

на плоскости параметров происходит по квадрату с удвоенной"

Рис. 6.9 .

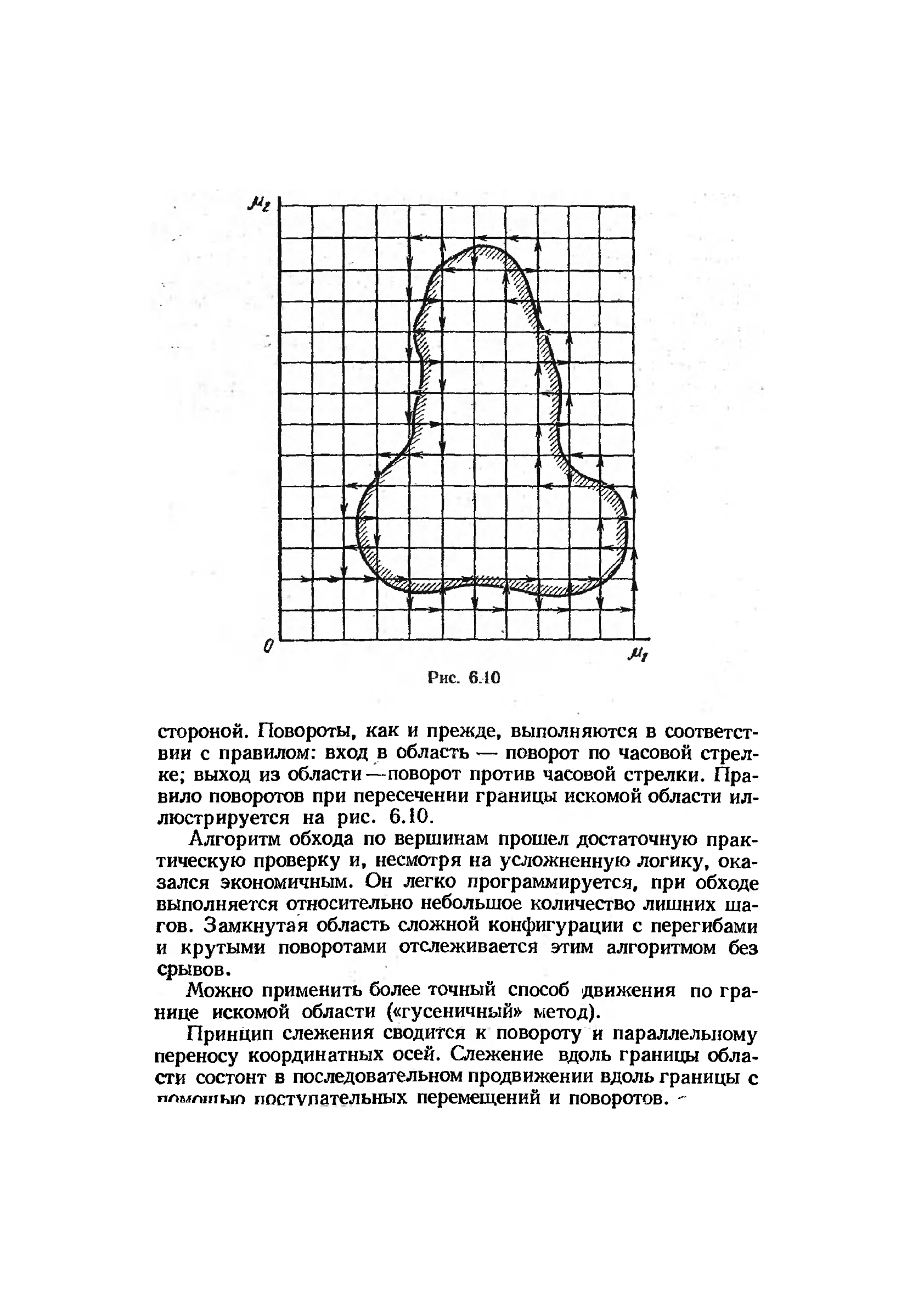
стороной. Повороты, как и прежде, выполняются в соответст-

вии с правилом: вход в область — поворот по часовой стрел-

ке; выход из области—поворот против часовой стрелки. Пра-

вило поворотов при пересечении границы искомой области ил-

люстрируется на рис. 6.10.

Алгоритм обхода по вершинам прошел достаточную прак-

тическую проверку и, несмотря на усложненную логику, ока-

зался экономичным. Он легко программируется, при обходе

выполняется относительно небольшое количество лишних ша-

гов. Замкнутая область сложной конфигурации с перегибами

и крутыми поворотами отслеживается этим алгоритмом без

срывов.

Можно применить более точный способ движения по гра-

нице искомой области («гусеничный» метод).

Принцип слежения сводится к повороту и параллельному

переносу координатных осей. Слежение вдоль границы обла-

сти состоит в последовательном продвижении вдоль границы с

ПЛМЛШЬЮ поступательных перемещений и поворотов. -

* * '

• » « Z - ;

Пусть имейся две точки lx

yj и [х

, ,yj, принадлежа-

щие искомой области на плоскости параметров fijfi

, и пусть

интересующая нас область лежит справа от прямой, соединяю^

щей точку [х

\ с [х

, */

]. Тогда приближенно можно указать

следующую точку по формулам

= 2Х

— x

; = 2У

—

. .

. •

Геометрически это означает, что сделан шаг по прямой,

соединяющей точки \х

] и 1х

, у

], от точки lx

] к точ-

ке [лг

, у

],' равной расстоянию между этими точками

(рис. 6.11, а, б).

В полученной точке с координатами 1х°

у°] вычисляется

функционал G (х°, у°1. При этом возможны два случая:

1. G 1А у

] — /> 0.

Анализируемая точка с координатами [я

, у°1 находится

вне искомой области. Тогда выполняется поворот против ча-

совой стрелки и производится определение положения новой

точки U

, у

] по формулам

= х

+ — х

] cos а

—W —у

\ sin а

; 1 ^

[х°—лг

] sfri

+ [у

—y

]

cos а

, j

где а

— угол поворота.

2. G у°] — I < 0.

Точка находится внутри искомой области. Для выхода на

границу осуществляется поворот по часовой стрелке. Положе-

ние новой точки определяется по формулам

^х

+ —Х

! cos а + [t/> — у

] sin

ее;

\ ^

^Уг—sin a +[tf— oleosa, j

В полученной точке вновь вычисляется функционал Q lx

\ и проверяется знак разности G 1х

, уЦ — /.

Если соблюдается условие G —• / = 0, то точка

находится точно на границе искомой области.

Если имеет место случай 1, то нахождение следующей

точки выполняется по формулам (6.76) в соответствии со зна-

ком разности G

[*<*>, у<

— /.

Эта процедура продолжается до тех пор, пока случай 1 не

перейдет в случай 2 или наоборот.

Переход сопровождается переменой знака разности

Угол а

делится на два или на три, и процесс продолжа-

ется до тех пор, пока угол а

не станет равным наперед задан-

ному малому значению. При практических расчетах величина

сб| ж

1°

отражает достаточную точность. Найденная таким об-

разом точка границы принимается за новое значение 1х

причем в качестве точки \х

\ берется прежняя точка U

1 и процесс повторяется.

Все точки получаются на одинаковом расстоянии от гра-

ницы, что не достигается при использовании алгоритма «блуж-

дания» по вершинам квадратов.

Объем вычислительной работы существенно уменьшается,

при использование малых и фиксированных углов поворота.

Приближенно можно считать sin cos — a

/2.

При a 5° ошибка составляет менее

Если точка находится внутри области, поворот по часовой

стрелке с учетом параллельного переноса в точку [x

]

осуществляется по формулам

=^х

+ (х°—х

)<1 —а

/2) + -у

) а;

У*

-« +

(у»

-у

)

—а

/2).

Если точка находится вие области, поворот против часовой

стрелки с учетом параллельного переноса в точку \х

]

выполняется по формулам

- х

~~х

) (1

-а

/2)-(/-у

) а;

• ••

^y* + {x

~xz)a + (y

-yi)(l ^а

/2). -

Вычисления в значительной степени упрощаются, если по-

вороты делать всегда на один и тот же угол. В этом случае для

конкретной задачи величины sin

ее

и cos а вычисляются только

один раз и входят постоянными коэффициентами в формулы.

Например, если взять а =

0,1

рад (5°43'46"), то имеем sin а =

= 0,09983; cos а ^ 0,99500. ~

Для данного угла имеем формулы:

а) при повороте по часовой стрелке

< I, точка внутри

области)

= х

+ 0,99500 — х

) + 0,09983 — у

У*

— 0,09983 (х° — х

) + 0,99500 (у

— у

);

б) при повороте против часовой стрелки (G > /, точка вне

области)

= х

+ 0,99500 — х

) — 0,09983 {у

— у

У*

+ 0,09983

(X*

— х

) + 0,99500

(у*

— у

Точность нахождения границы увеличивается при исполь-

зовании малых углов.

Если отслеживаемый контур имеет сложную конфигурацию,

то процедуру построения границы можно разделить на два

этапа: поиск и уточнение границы. В режиме поиска исполь-

зуются большие углы; в режиме уточнения — малые. Величи-

на угла а

может быть выбрана из условия окончания слеже-

ния на каждом шаге:

h < 8,

где Л — шаг; е — заданная точность.

Если заданы точность и шаг, то угол определяется по фор-

муле а

в/Л.

Движение вдоль участков границы со сложной конфигура-

цией может осуществляться с переменным шагом. При введении

переменного шага в формулы вносятся изменения. Пусть дли-

на шага при переходе из точки lx

yj в точку lx

\ равна 1

а из точки [х

] в точку [л:

, у

] равна t

Тогда q = ljl

— число, показывающее, во сколько раз

следующий шаг меньше предыдущего.

Координаты новой точки находятся по формулам я? =

= (я + 1) X* — У\ = to + 1) г/з —

ЯУг-

Использование переменного шага и угла приводит к адап-

тивному способу слежения вдоль границы. В зависимости от

условий движения, конфигурации области и других факторов