Воронов А.А. Теория автоматического управления. Часть первая
Подождите немного. Документ загружается.


Переходим к построению желаемой ЛАЧХ. ЛАЧХ неизменяемой
части имеет требуемый порядок астатизма и передаточный коэффици-
ент, поэтому низкочастотная асимптота желаемой ЛАЧХ совпадает с
низкочастотной асимптотой ЛАЧХ неизменяемой части системы.
Для заданного значения о — 30% по номограмме (см. рис. 5.24)
определяем
Ршах = 1,27 и /р~3,5л/со
С
р.
Вычисляем нижний предел частоты среза желаемой ЛАЧХ:
со
С
р1 = 3, 5я/*
р
= 3, 5я /0,5 = 22с-
1
.
По (5.39) находим верхний предел частоты среза;
<0cp2^Vw/g
0
УёоТбТГ = 22,4 с-
1
.
Выбираем со
с
= 22 с""
1
и через эту точку проводим среднечастотнук>
асимптоту желаемой ЛАЧХ с рекомендованным ранее наклоном
— 20 дБ/дек (рис. 5.28). Далее по кривым (см. рнс. 5.25) для Р
тах
—
= 1,27 определяем, что необходим избыток фазы у — 40° при ордина-
тах (со), лежащих в пределах = 14 дБ. Проводим прямую с ор-
динатой + 14 дБ и из точки пересечения ее со среднечастотной асимп-
тотой желаемой ЛАЧХ строим пробную сопрягающую асимптоту с на-
клоном — 40 дБ/дек.
Пусть высокочастотной асимптотой желаемой ЛАЧХ будет высо-
кочастотная асимптота ЛАЧХ неизменяемой части системы. Сопряже-
ние среднечастотной асимптоты желаемой ЛАЧХ с высокочастотной
начинаем при частоте со
2
.
Теперь нужно проверить избыток фазы при контрольных частотах
со
а
и cog. Воспользуемся номограммой для подсчета фазы по асимптоти-
ческой ЛАЧХ, изображенной на рис. 5.26.
Подсчитываем фазу при частоте со
а
:
<Ра = —20 (2,25 —2,04) — 40 (2,04—0) — 20 (2,16—0)
— 40(2,2—2,16) — 60 (2,25 — 2,2) = — 133,6°.
Следовательно, избыток фазы
Ya = 180—133,6 = 46,4°.
Подсчитываем фазу при частоте cog:
фа
= —20 (2,25—2,22)— (40 (2,22—2,16) — 20 (2,16—0,24)—
— 40 (0,24+1,12)—60 (2,25—1,12) - — 163,6°.
Избыток фазы при этой частоте
Y6 = 180—163,6= 16,4°.
При частоте со
а
избыток фазы превышает требуемое значение на
6°. Допустимо, однако, лишь незначительное перемещение сопрягающей
асимптоты вправо. Оно не расширит сколько-нибудь заметно диапазон
пропускания нижних частот, поэтому останавливаемся ,иа выполнен-
ном сопряжении.
Избыток фазы прн частоте cog значительно меньше допустимого.
Для его увеличения высокочастотную асимптоту желаемой АЧХ нуж-

Рис. 5.29
но сместить вправо.
При этом усложнится
корректирующее устрой-
ство.
Попробуем прове-
рить качество системы
при составленной же-
лаемой ЛАЧХ и затем
будем решать вопрос о
целесообразности ее из-
менения.
По L
m
(со) составля-
ем передаточную функ-
цию разомкнутой скор-
ректированной системы:
k (s
/со а
+ 1)
S (s/C0
3
+ 1) (S/0)2+ 1) (s/0>4+ 1)
200 (0,24s+l)
s (2,17s+1) (0,01s+ 1) (0,00574s+ S)
где co
3
= 0,46c
—i
—i
10-
7
s
4
+
co
a
= 4,2c-
1
; co
2
= 100c-
1
; co
4
=174c
Передаточная функция замкнутой системы
W
g
(s) = WWII + w (s)] = (0,24 S + l)/(6,25
+ 1,74- !0-
4
s
3
+0,01 ls?+ 0,245 s + 1).
Вещественная частотная характеристика, вычисленная по частот-
ной передаточной функции Wg (/со), представлена на рис. 5.29. Пост-
4
роенная по ней переходная характеристика показана на рис. 5.30.
Показатели качества а = 14% и 0,4 с удовлетворяют требо-
ваниям. Перерегулирование даже значительно меньше допустимого,
поэтому составленную желаемую ЛАЧХ можно ие изменять.
Несоответствие показателей качества с их расчетными значения-
ми объясняется значительным отличием вида вещественной частотной
характеристики скорректированной системы (рис. 5.29) от типовой, по
которой составлены номограммы (см. рис. 5.24 и 5.25). *
Вычитая из желаемой ЛАЧХ
1
Ж
(со) ЛАЧХ L
0
(
w
) неизменяе-
мой части системы, получаем
ЛАЧХ последовательного кор-
ректирующего устройства L
K
(со)
(см. рис. 5.28). По этой ЛАЧХ
составляем полиномы R
K
(s) и
Q
K
(s) числителя и знаменателя
передаточной функции корректи-
рующего устройства:
Як (S) = (s/co
a
+ 1) (s/щ + 1)=
= (0,24 s + 1) (0,05 s + 1);
QK
(S) = (s/co
3
+
1)
(s/щ + 1) =
= (2,17s + 1) (0,0 0574s + 1).
Рис. 5.30
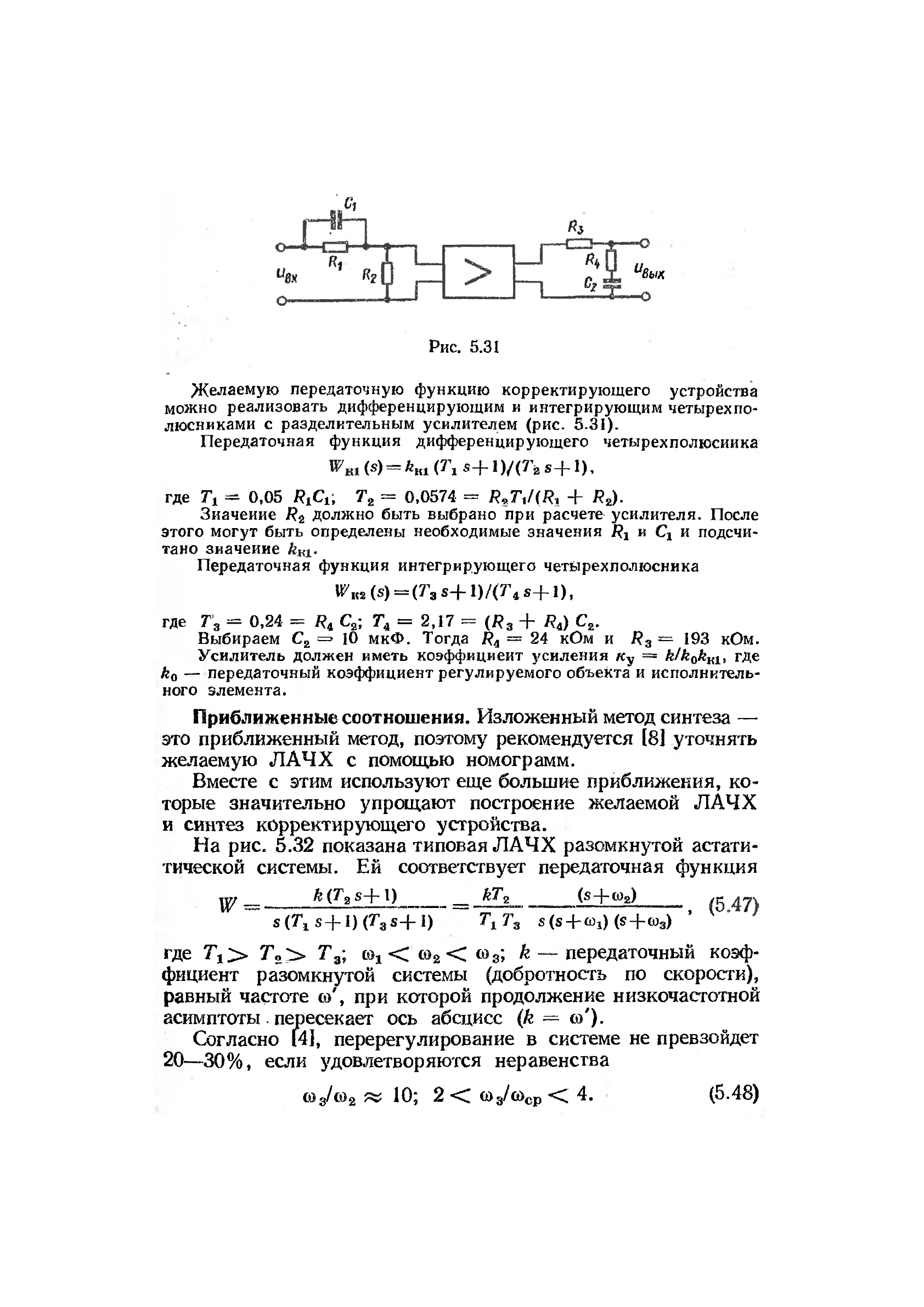
и
вык
Рис. 5.31
Желаемую передаточную функцию корректирующего устройства
можно реализовать дифференцирующим и интегрирующим четырехпо-
люсниками с разделительным усилителем (рис. 5.31).
Передаточная функция дифференцирующего четырехполюсника
<s)
= V V\s+ \)/(7\s+l),
где T
t
- 0,05 RtCu Т
2
- 0,0574 - + Д
2
).
Значение R
2
должно быть выбрано при расчете усилителя. После
этого могут быть определены необходимые значения R
1
и С
г
и подсчи-
тано значение
Передаточная функция интегрирующего четырехполюсника
W
K
z(s) = (T
3
s+l)/0\s+\)
t
где Т
3
- 0,24 - /?
4
С
2
; Г
4
= 2,17 = (R
3
+ tf
4
) С
2
.
Выбираем С
2
10 мкФ. Тогда R
4
= 24 кОм и R
3
— 193 кОм.
Усилитель должен иметь коэффициент усиления Ку = k/k
0
k
Kti
где
k
0
— передаточный коэффициент регулируемого объекта и исполнитель-
ного элемента.
Приближенные соотношения. Изложенный метод синтеза —
это приближенный метод, поэтому рекомендуется [8] уточнять
желаемую ЛАЧХ с помощью номограмм.
Вместе с этим используют еще большие приближения, ко-
торые значительно упрощают построение желаемой ЛАЧХ
и синтез корректирующего устройства.
На рис. 5.32 показана типовая ЛАЧХ разомкнутой астати-
тической системы. Ей соответствует передаточная функция
w ~ k(T
2
s+\)
=
kT
2
_
(5
+ to
2
)
5(^5+1)^35+1)" Т
Х
Г
3
5(5 + 0)^ (S + C0
3
) '
где T
x
^> Т
э
;
coj
< со
2
< со
3
; k — передаточный коэф-
фициент разомкнутой системы (добротность по скорости),
равный частоте со', при которой продолжение низкочастотной
асимптоты пересекает ось абсцисс (k — со').
Согласно [41, перерегулирование в системе не превзойдет
20—30%, если удовлетворяются неравенства
со3/со2 ^ 10; 2< 0>
3
/а>
ср
< 4. (5.48)

Рис. 5.32
При этом время регулирования с достаточной точностью оп-
ределяется по частоте среза:
t
v
^ п/о>
ср
. (5.49)
Следовательно, заданное значение k определяет частоту
со' и затем можно построить прямую, на которой будет лежать
низкочастотная асимптота желаемой ЛАЧХ.
С другой стороны, заданное значение времени регулирова-
ния t
v
позволяет определить по (5.49) частоту среза со
ср
же-
лаемой ЛАЧХ. Остается выбрать частоту со
2
и ш
3
так, чтобы
удовлетворялись неравенства (5.48).
В результате оказываются известными желаемая ЛАЧХ
и передаточная функция разомкнутой системы. Зная переда-
точную функцию неизменяемой части системы, можно опреде-
лить необходимую передаточную функцию последовательно-
го корректирующего устройства.
Неравенства (5.48) определяют частоты со
2
и со
3
не одно-
значно. Поэтому удобно сразу же рассматривать несколько
вариантов значений со
2
и со
3
. Затем выбрать тот из них, при
котором система имеет требуемые показатели качества. Для
их определения необходимо, конечно, строить переходные ха-
рактеристики замкнутой системы.
Используют и другие приближенные соотношения для по-
строения желаемой ЛАЧХ. Иногда, особенно при предвари-
тельных расчетах, они оказываются весьма удобными.

I r.T.v.-;;::
1
:
МАШИННАЯ РЕАЛИЗАЦИЯ
МЕТОДОВ ТЕОРИИ
АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
§6.1. Математические модели
автоматических систем и особенности
реализации их на ЭВМ
Возможности современной вычисли-
тельной техники позволяют значи-
тельно ускорить сроки проектиро-
вания автоматических систем управле-
ния объектами различного назначе-
ния. Успех в решении задачи в зна-
чительной степени зависит от основных
факторов: математической изученности
управляемого объекта, т. е. от того, на-
сколько адекватно составлено математи-
ческое описание функционирования
объекта, эффективности прикладных ме-
тодов теории автоматического управле-
ния, уровня развития вычислительных
методов, наличия высококачественного
программного обеспечения, от того, на-
сколько успешно используется творче-
ский потенциал исследователя-проекти-
ровщика. При этом решающей фактор
остается за человеком, который может
решать многие неформализованные зада-
чи. Именно этот фактор стимулирует
развитие диалогового проектирования.
Основа автоматизированного проек-
тирования — математическое описание
функционирования системы. В настоя-
щее время преобладают и широко ис-
пользуются три способа математическо-
го описания автоматических систем: 1)
метод передаточных функций и тесно
связанные с ними частотные характе-
ристики;
2)
метод переменных состояния;
3) структурно-топологические методы.

Метод передаточных функций, по существу, представляет
собой применение преобразования Лапласа и частотной теории
для изучения качественного поведения решений обыкновенных
дифференциальных уравнений. Созданные для проектирова-
ния систем с одним входом и одним выходом передаточные
функции и частотная теория до сих пор являются основными
инженерными методами со сложившейся методологией. Непо-
средственное изучение исходных дифференциальных уравнений
с заданными начальными условиями заменяется в этих методах
исследованием алгебраических свойств некоторых функций,
порождаемых системой дифференциальных уравнений. На-
пример, критерий Михайлова и Найквиста основаны на изу-
чении именно таких функций.
На разработку и усовершенствование Частотных методов
были затрачены десятилетия; несмотря на «машинный век»,
они не утратили своего значения и не исчерпали всех возмож-
ностей. Многолетние исследования показали, что по глубине
и степени завершенности частотные методы во многих случаях
не имеют вполне эквивалентный замены, а модификация их
применительно к ЭВМ позволяет получать весьма ценную ин-
формацию о проектируемой системе в сжатые сроки. В 70-е
годы Г. Розенброком [19] был создан метод «размытых» частот-
ных характеристик, предназначенный для автоматизирован-
ного проектирования систем с несколькими входами и выхо*-
дами. Дальнейшее развитие метода было осуществлено
В. В. Солодовниковым и его учениками [131.
В основе метода переменных состояния лежит представле-
ние дифференциальных уравнений в нормальной форме Коши,
которое дополняется алгебраическими уравнениями, связы-
вающими выходные переменные с переменными состояния
x-Ax + Bu;
(б1)
у-=Сх,
где А, В, С — матрицы коэффициентов размерности п X п,
п X т, г X п соответственно; и — вектор возмущающих воз-
действий; т — число входов; г — число выходов.
Математическим аппаратом метода переменных состояния
(МПС) являются матричное исчисление и вычислительные ме-
тоды линейной алгебры. Метод переменных состояния содей-
ствовал значительному развитию теории управления. На язы-
ке МПС выполнена большая часть работ по оптимальному уп-
равлению, фильтрации, оцениванию. В настоящее время в те-

ории автоматических систем управления наметилось плодо-
творное сочетание метода переменных состояния с частотными
методами. Оба способа описания взаимосвязаны и дополняют
друг друга.
Топологические методы опираются на использование мето-
дов теории графов. Они получают все большее распростра-
нение, однако эффективность их применения во многом зависит
от принципиальных результатов, полученных в теории гра-
фов.
С точки зрения автоматизации проектирования систем уп-
равления с помощью топологических методов представляет
интерес задача формирования передаточных функций по струк-
турным схемам. Если структура системы выбрана, то, исполь-
зуя передаточные функции динамических звеньев и известные
правила преобразования структурных схем, можно сравни-
тельно легко составить программу получения передаточной
функции разомкнутой или замкнутой системы при управляю-
щих или возмущающих воздействиях. Программа нахождения.
передаточной функции сводится к раскрытию скобок, приведе-
нию подобных членов и упорядочиванию коэффициентов по
убывающим степеням полинома. Такая программа часто явля-
ется основной при машинных исследованиях (анализ устойчи-
вости, построение частотных характеристик, построение обла-
стей устойчивости, D-разбиение в плоскости параметров и т. д.).
Автоматизация формирования передаточных функций позволя-
ет вести параметрический синтез и анализировать различные
структуры. Такие программы успешно применялись для по-
строения передаточных функций сложных систем с перекре-
щивающимися обратными связями. Уязвимое место таких про-
грамм — частые случаи переполнения разрядной сетки ввиду
плохой «обусловленности» полинома. Кроме того, существуют
технические трудности при программировании, так как неко-
торые алгоритмические языки (АЛГОЛ ФОРТРАН) не при-
способлены для обработки буквенно-символьной информации.
Решение подобных задач стало эффективным на основе тополо-
гических методов. Так, использование методов теории графов
в сочетании со структурными числами дает возможность полу-
чать передаточные функции по любой структуре на языке
ФОРТРАН.
Метод переменных состояния ориентирован на вычисли-
тельные методы теории матриц. Если требуется выполнить
анализ устойчивости по уравнениям переменных состояния
(6.1), то традиционные способы требуют предварительного

приведения матрицы А к характеристическому урав-
нению
| А — sE |
—
(—
1
)
л
+ s
n
~
1
+... + а
п
) = 0 (6.2)
с последующим применением критериев устойчивости или кор-
невых методов. Существующие критерии устойчивости (Рау-
са, Гурвица, Льенара—Шипара, Михайлова) могут применять-
ся только непосредственно к коэффициентам характеристиче-
ского уравнения замкнутой системы. Методы локализации соб-
ственных чисел матрицы А (Гершгорина, Островского, Бра-
узра и др.) дают лишь достаточные условия и малопригодны
для широкого использования.
Получение коэффициентов характеристического уравнения
часто связано с серьезными трудностями вычислительного
характера, несмотря на наличие стандартных программ, по-
строенных на известных методах. Применительно к задачам
машинного анализа и синтеза сложных автоматических систем
многие методы не вполне подходят из-за чувствительности к
«частным особенностям» матрицы или потери точности из-за
роста погрешности вследствие накопления ошибок округле-
ния.
В последнее время были созданы способы определения всех
собственных чисел матрицы А, не связанные с операцией вы-
числения коэффициентов характеристического уравнения. Они
основаны на представлении матрицы А в виде произведения
ортогональной и почти треугольной форм. Наибольшей уни-
версальностью обладают QR- и QL-алгоритмы. Сущность QR:
алгоритма состоит в представлении исходной матрицы А в ви-
де произведения двух матриц: ортогональной Q и верхней
треугольной R (нижней треугольной L в случае (^-алгорит-
ма). Предварительно матрица А преобразуется к форме Хассен-
берга Н, а QjR-алгоритм всегда предполагает, что такое при-
ведение выполнено. Матрица Н является верхней треуголь-
ной матрицей, но с наличием субдиагональных элементов. На-
пример, матрица Хассенберга размерности (4 X 4) имеет вид
Ф
О * * *
о о * *
Процедура метода предусматривает построение матрицы,
подобной матрице А, но имеющей клеточную треугольную
структуру с диагональными блоками 1X1 или 2X2 и теми же
(6.3)

собственными числами, что и исходная матрица А. Приведе-
ние исходной матрицы А к матрице Хассенберга Н осущест-
вляется для сокращения числа операций и экономии машин-
ного времени. Различные способы (например, метод Хаусхол-
дера и метод Гивенса) приведения к матрице Н рассматривают-
ся в работах по линейной алгебре.
В теоретическом отношении QR- и QL-алгоритмы мало раз-
личаются. <2#~алгоритмы эффективнее использовать, когда
большие элементы матрицы сосредоточены в нижнем правом
углу, a QL-алгоритм — когда большие элементы матрицы со-
средоточены в левом верхнем углу. При правильной реализа-
ции алгоритма на ЭВМ ошибки округления во многих случа-
ях не оказывают большого влияния на точность нахождения
собственных чисел матрицы А. Описание и особенности машин-
ной реализации QR- и QL-алгоритмов более подробно изло-
жены в [4, 5, 14, 151.
Особенности машинных вычислений в задачах автоматиче-
ского управления. Успех в решении задач автоматизирован-
ного проектирования автоматических систем во многом опре-
деляется тем, как в действительности осуществляются дейст-
вия над числами в ЭВМ. Существенная особенность машинных
вычислений — влияние ошибок округления. Как бы точно ни
осуществлялись операции над числами, для их представления
отводится конечное число знаков и они должны быть округ-
лены.
В современных цифровых ЭВМ расчеты, как правило, вы-
полняются в режиме с плавающей запятой. Это связано с пред-
ставлением чисел, сильно различающихся по абсолютной вели-
чине. Число разрядов в мантиссе достигает 15 и выше (в деся-
тичных знаках), и все же встречаются задачи, где такой точ-
ности недостаточно.
Иногда возникает вопрос, почему вообще нужна такая
точность вычислений, как 10~
12
и выше, В большей части за-
дач науки и техники исходные данные в лучшем случае имеют
точность 10~
3
—10 а часто она не достигает и 10~
2
или бы-
вает еще ниже. На раннем этапе создания цифровых вычисли-
тельных машин Дж. Нейман показал, что для получения точ-
ности конечного результата, равной 10~
3
, требуется точность
промежуточных вычислений в арифметических операциях
10~
12
. Кроме того, существует эффект усиления ошибок, обра-
зовавшихся от предшествующих операций. Это усиление в
принципе может быстро покрыть любой разрыв. Например,
отношение 10~
3
и 10~
12
образуют разрыв 10
9
. Дж. Нейман

привел пример, когда 425 последовательных операций, каж-
дая из которых усиливает ошибку только на 5%, заполняют
этот разрыв. Разумеется, приведенный пример лишь иллю-
стрирует важность проблемы получения верных результатов
в условиях накопления ошибок округления. В действитель-
ности в реальных машинах результаты округления не столь
неблагоприятны. Все же при решении сложных задач прихо-
дится считаться с ошибками накопления в результате округ-
ления.
В режиме с плавающей запятой почти во всех случаях
происходит округление и в окончательных результатах могут
наблюдаться существенные, искажения. Результаты округле-
ний, какими бы малыми они ни были, меняют свойства арифме-
тических операций. Свойства ассоциативности и дистрибутив-
ности не выполняются на существующих ЭВМ. Произведение
сомножителей, отличных от нуля, может оказаться равным
нулю (это явление известно как «возникновение машинного
нуля при умножении»). Свойство коммутативности соблюдает-
ся лишь в том случае, если имеет место «правильное» округле-
ние [4, 51.
Формирование процесса правильного округления в совре-
менных ЭВМ, работающих в двоичной системе счисления, за-
труднительно. В системе счисления с четным основанием ок-
ругление реализуется неоднозначно. Считается невозможным
построить процесс округления в «классическом» виде, основан-
ный лишь на анализе конца мантиссы, таким образом, чтобы
ошибки компенсировали друг друга. Следовательно, на ЭВМ,
по существу, реализуются новые операции, лишь приближен-
но изображающие обычные арифметические операции. Отме-
ченные особенности не могут быть устранены техническими
средствами, хотя точность может быть значительно уве-
личена. Существуют большие возможности увеличения точ-
ности. Они заключаются в применении переменной длины ман-
тиссы, в использовании сокращенных систем счисления (на-
пример, троичной). -
Распространенным способом анализа точности является
решение задачи с обычной и удвоенной точностью. Совпадение
результатов указывает на отсутствие ошибок округления, по-
этому считается, что остальные вычисления в сходных зада-
чах можно вести с обычной точностью. Такой подход распро-
странен и часто дает удовлетворительные результаты.
Другой подход заключается в использовании специальных
программ, позволяющих записывать числа и выполнять one-
