Воронов А.А. Теория автоматического управления. Часть первая

Подождите немного. Документ загружается.

Если

= WJW = 1 /(W

WbWJ

(5.33)

то передаточная функция относительно задающего воздейст-

вия обращается в единицу, а передаточная функция для ошиб-

ки слежения — в нуль. Следовательно, (5.33) — это условие

инвариантности ошибки слежения е от задающего воздейст-

вия, или условие идеального воспроизведения выходной ко-

ординатой у задающего воздействия g.

Выполнение (5.33) связано с большими трудностями, не-

жели выполнение (5.30). Причина в том, что сигнал форси-

рующей цепи должен преодолеть не только инерционность ис-

полнительного элемента регулятора, но и регулируемого

объекта.

Ранее указывалось на практическую невозможность созда-

ния производных выше второго порядка, поэтому в комбини-

рованных следящих системах достигается лишь частичная ин-

вариантность ошибки в от задающего воздействия g до нулевой,

первой или второй производной включительно. Это означает

соответственно астатизм первого, второго и третьего поряд-

ков относительно задающего воздействия.

Неизбежная (хотя и незначительная) инерционность диф-

ференцирующих элементов, а также неточности в определе-

нии параметров и изготовлении элементов регулятора ведут к

тому, что и частичная инвариантность обеспечивается лишь

с точностью до малой величины 6.

Несмотря на это, комбинированное регулирование значи-

тельно увеличивает точность слежения и находит широкое

применение. Чем медленнее изменяется задающее воздействие

g> тем больший эффект дает частичная инвариантность в

от g.

При наличии форсирующей цепи роль замкнутого контура

следящей системы уменьшается и он может быть выполнен из

более простых элементов. Форсирующая цепь не влияет на

устойчивость замкнутого контура, но сама эта цепь должна

быть устойчивой.

Если в комбинированной следящей системе имеется силь-

ное возмущение, то точность слежения может быть увеличе-

на еще более созданием компенсирующей связи по этому воз-

мущению. Преобразовательные элементы обеих цепей частично

могут быть объединены, и может оказаться, что для создания

компенсирующей цепи потребуется только элемент, измеряю-

щий возмущение.

§ 5.5. Обеспечение устойчивости и повышение

запаса устойчивости

Способы придания системам автоматического регулирова-

ния устойчивости и достаточного запаса устойчивости (спосо-

бы стабилизации и демпфирования) разнообразны. В § 5.2

рассматривалась возможность решения этой задачи выбором

основных элементов регулятора и изменением их динамиче-

ских свойств с помощью местных обратных связей. Выясним,

как влияет на устойчивость изменение наиболее характерно-

го параметра — постоянной времени апериодического звена.

На рис. 5.16 сплошными линиями изображены логарифми-

ческие частотные характеристики разомкнутой системы с пе-

редаточной функцией (5.26). При увеличении Т

с 0,5 до 1 с

характеристики принимают положение, показанное пунктир-

ными линиями. Увеличение постоянной времени Т

приводит

к увеличению запаса устойчивости по фазе с у

—

26° до у

— 60°. Заметим, что сопрягающая частота щ = МТ

располо-

жена левее частоты среза ш

ср

Если же сопрягающая частота апериодического звена рас-

положена правее частоты среза о>

ср

, то увеличение постоян-

ной времени этого звена уменьшит запас устойчивости. Оче-

видно, что изменение постоянной времени колебательного зве-

на влияет на запас устойчивости аналогичным образом. Влия-

ние постоянной времени форсирующего звена [звена с переда-

точной функцией = k (Ts +1)] противоположно.

Итак, если сопрягающая частота апериодического или ко-

лебательного звена расположена левее частоты среза логариф-

мической амплтудно-частотной характеристики разомкнутой

480° -

W -

20 -

ОгО =

L(o>)

Рис. 5.16

системы, а сопрягающая

частота форсирующего

звена расположена пра-

вее частоты среза, то

увеличение постоянной

времени каждого из этих

звеньев ведет к увеличе-

нию запаса устойчивости?

[4]. Указанная зависи-

мость справедлива лишь

при условии, что сопря-

гающая частота раско-

ложена на некотором удалении (около одной декады) от ча-

стоты среза.

Встречаются, од&ако, структуры, для которых указанное

правило не выполняется. Пусть, например, передаточная

функция разомкнутой системы

W = k (Т

+ l)/[T

s + 1) (T

s + 1) (7> + 1)1,

где k = 100; Т

= 0,1 с; Г, = 1 с; = 0,5 с; 7

= 0,01 с.

Логарифмические частотные характеристики этой систе-

мы показаны на рис. 5.17 сплошными линиями. При изменении

до 10 с характеристики принимают положение, показан-

ное на рис. 5.17 пунктиром. Запас устойчивости по фазе с

у = 61° уменьшился до у

= 47°.

Другой и наиболее применяемый путь стабилизации и дем-

пфирования системы — введение в ее прямую цепь дополни-

тельных звеньев. С этой целью используют сложные динамиче-

ские звенья.

В зависимости от структуры и параметров системы введе-

ние одного и того же звена может дать различные результаты.

Так, в § 5.4 уже было показано, что введение интегрирующего

звена может вести и к уменьшению, и к увеличению запаса

устойчивости. Поэтому правильный выбор дополнительного

звена можно сделать только зная структуру и параметры си-

стемы.

Рассмотрим наиболее характерные случаи стабилизации

и демпфирования систем путем введения дополнительных зве-

ньев. Предположим, что разомкнутая система описывается пе-

редаточной функцией (5.26) при k = 100; Т

= 0,05 с; Т

= 0,01 с и Т

= 0,001 с. В разомкнутом состоянии система

устойчива и ее логарифмические частотные характеристики,

изображенные на рис. 5.18 сплошными линиями, свидетель-

ствуют о неустойчивости замкнутой системы, так как фаза

достигает —180° при частоте, меньшей частоты среза.

Введем в прямую цепь системы дополнительное звено с пе-

редаточной функцией W

= 1/(Тд5 + 1), где Т

= 8 с. Тог-

да характеристики системы принимают положение, показан-

ное на рис. 5.18 пунктирными линиями, и на основании их

можно видеть, что замкнутая система становится устойчивой.

Запас по фазе составляет у

= 51°. Увеличением постоянной

времени Т

дополнительного звена запас устойчивости по фа-

зе можно увеличить.

Устойчивость достигнута введением апериодического зве-

на, постоянная времени которого значительно больше постоян-

ных времени имеющихся апериодических звеньев. При этом

высокочастотная часть логарифмической амплитудно-частот-

ной характеристики сместилась вниз. Так же изменилась и

логарифмическая фазочастотная характеристика. Такой при-

ем обеспечения устойчивости или повышения запаса устойчи-

вости называют демпфированием с подавлением высоких ча-

стот (демпфированием с внесением отрицательных фазовых

сдвигов).

Апериодическое звено с большой постоянной времени

представляет собой фильтр низких частот и подавляет высоко-

частотные помехи. В этом достоинство данного вида демпфиро-

вания. Значительное уменьшение частоты среза и, следователь-

но, быстродействия системы является весьма существенным не-

достатком.

Если ось абсцисс пересекается асимптотой ЛАЧХ, имею-

щей наклон — 20дБ/дек, и слева от частоты среза са

ср

только

одна сопрягающая частота, то система остается устойчивой и

запас устойчивости не изменяется при увеличении передаточ-

-90°

Or о

о -20

LCco)

-180°

Рис. 5.18

ного коэффициента k разомкнутой системы. Нужно только

одновременно с увеличением k пропорционально увеличивать

постоянную времени апериодического звена. Предположим

далее, что в рассматриваемую систему введено дополнитель-

но идеальное форсирующее звено с передаточной функцией

= T

s + I, где 7*

= 0,01 с. На рис. 5.19 изображены

логарифмические частотные характеристики разомкнутой це-

пи исходной системы (сплошные линии) и системы с дополни-

тельным звеном (пунктирные линии). В замкнутом состоянии

система с дополнительным звеном будет устойчивой, запас по

фазе составляет у

= 43°.

Теперь устойчивость достигнута введением не апериодиче-

ского, а форсирующего звена. В результате высокочастотная

часть ЛАЧХ сместилась вверх. Такое же изменение и у ЛФЧХ,

поэтому данный прием называют демпфированием с подняти-

ем высоких частот (демпфированием с внесением положитель-

ного фазового сдвига).

Введением форсирующего звена могут быть обеспечены

устойчивость и необходимый запас устойчивости при любой

передаточной функции исходной системы (если она становится

структурно устойчивой). Одновременно увеличивается и бы-

стродействие. Однако существенно увеличивается и влияние

высокочастотных помех. Последнее обстоятельство является

серьезным недостатком данного вида демпфирования и огра-

ничивает его применение.

Предположим еще, что в рассматриваемую систему введено

дополнительно сложное звено с передаточной функцией

«7

= (Г

2д

s +

(Т

3д

+ 1 )/[Г

1д

s -'

(Г*

s + 1)1,

где Г

1д

- 0,1 с; Т

2д

- 7

3д

= 0,01 = 0,001 с.

На рис. 5.20 показаны логарифмические частотные харак-

теристики разомкнутой цепи исходной системы (сплошные ли-

нии) и системы с дополнительным звеном (пунктирные линии).

В замкнутом состоянии система с дополнительным звеном ус-

тойчива, запас устойчивости по фазе у

= 49°.

Устойчивость достигнута смещением вниз среднечастоткой

части ЛАЧХ, и данный прием называют демпфированием с

подавлением средних частот. Этот вид демпфирования проме-

жуточный между двумя первыми, и применяют его наиболее

часто.

Рассмотренные приемы стабилизации и демпфирования си-

стем автоматического регулирования являются основными, но

далеко не исчерпывают всех возможностей.

§ 5.6. Выбор параметров и синтез корректирующих

устройств по корневым годографам

Наглядность и простота исследования влияния отдельных

параметров системы на ее динамические свойства составляют

несомненные достоинства метода корневых годографов и обус-

ловливают его применение как для выбора параметров, так

и для синтеза корректирующих устройств.

Пусть требуется выбрать какой-то параметр а (передаточ-

ный коэффициент элемента, постоянную времени, коэффициент

демпфирования). Тогда при постоянных значениях всех ос-

тальных параметров нужно задавать различные значения а

х>

... внутри возможных пределов изменения этого параметра

в данной системе и построить траектории корней (корневой

годограф). Затем можно выбрать такое значение а, при кото-

ром имеет место наиболее благоприятное расположение нулей

и полюсов. Корни следует вычислять наиболее простым чис- -

ленным методом, так как большой точности не требуется из-за

приближенности корневой оценки качества.

Для выбора значения передаточного коэффициента k ра-

зомкнутой системы необходимо построить корневой годограф

при изменении k. Способ построения такого корневого годогра-

фа разработан весьма детально (см. § 4.6).

При синтезе корректирующего устройства используют раз-

личные исходные положения. В простейшем случае полагают,

что переходный процесс зависит от ближайшего к мнимой оси

вещественного полюса. Вместе с тем пользуются и предположе-

нием, что наилучшие динамические свойства система имеет,

когда ближайшей к мнимой оси будет пара комплексно-сопря-

женных полюсов. Однако добавление третьего ближайшего к

мнимой оси вещественного полюса обычно улучшает качество

переходного процесса.

Необходимо также учитывать влияние нулей передаточ-

ной функции, поэтому для определения качества переходно-

го процесса наиболее правильно рассматривать три ближай-

ших полюса и один нуль передаточной функции замкнутой

системы.

Порядок синтеза также может быть различным. Пусть тре-

буется выбратё последовательное корректирующее устройст-

во по заданным показателям качества переходной характери-

стики и при заданном значении передаточного коэффициента

k разомкнутой системы. Тогда можно поступать следующим

образом [1]: выяснить влияние k на показатели качества; по-

строить корневой годограф нескорректированной системы при

изменении k и отыскать на нем точки, соответствующие задан-

ным показателям качества; добиться прохождения траек-

торий корней при заданном значении k вблизи выбранных

точек, вводя дополнительные нули и полюсы; составить пе-

редаточную функцию последовательного корректирующего

устройства по дополнительно введенным нулям и полюсам.

Следует иметь в виду, что при введении диполя, т. е. полю-

са и нуля, близко расположенных друг к другу, показатели

качества почти не изменяются, но передаточный коэффициент

может быть увеличен.

Пример расчета по изложенной схеме приведен в [1].

Предположим, что динамика системы определяется парой

комплексно-сопряженных полюсов:

%,02

= —сс

± /Ч- (5.34)

Тогда передаточная функция замкнутой системы

(s)

= ft

/(r§ s

+ 2Г

s + 1), (5.35)

На основании переходной характеристики, соответствую-

щей этой передаточной функции, определяют зависимость а

и to

от времени регулирования /

и относительно перерегули-

рования сг [3], т. е.

«3/f

; а —е~

яа

«/

°о. (5.36)

Теперь синтез последовательного корректирующего уст-

ройства по заданным значениям ft, и сг будет слагаться из

следующих этапов:

1. Намечают положение определяющей пары полюсов s

и s

, т. е. пары полюсов передаточной функции (5.35), кото-

рая приблизительно эквивалентна передаточной функции скор-

ректированной системы на основании^заданных показателей

качества t

и а. При этом используют соотношения (5.36).

На диаграмме достаточно отметить только один полюс s

2. Наносят на диаграмму полюсы и нули неизменяемой

части системы.

3. Вводят дополнительные нули и полюсы так, чтобы тра-

ектория корней скорректированной системы при изменении

k проходила вблизи полюса s

.Желательно скомпенсировать

нулями ближайшие к мнимой оси полюсы неизменяемой ча-

сти системы, с тем чтобы влияние полюсов s

и s

на динами-

ку системы было действительно определяющим. Точка s

будет принадлежать траектории корней скорректированной

системы, если удовлетворяется уравнение фаз (4.36).

4. Вводят диполь так, чтобы передаточный коэффициент

ft имел необходимое значение. При этом' для вычисления ft

используют (4.37).

5. Составляют передаточную функцию последовательного

корректирующего устройства по введенным полюсам и нулям.

6. Для проверки выполнения требований строят переход-

ную характеристику скорректированной системы.

Пример 5.1. Передаточная функция неизменяемой части системы

Wo (s) =• k/ls

(0,1 s-f-

I) (0,05s + 1)].

Требуется выбрать последовательное корректирующее устройство,

обеспечивающее при fc > 10 следующие показатели качества: 0,5 с <

< /р < 0,7 с; 20% < о <

< 30%.

Подставляя в (5.36) /р =

= 0,5 и 0 = 0,2, получаем

«о

—

б; е~

8/сй

°-0,2;

соо— И

,2.

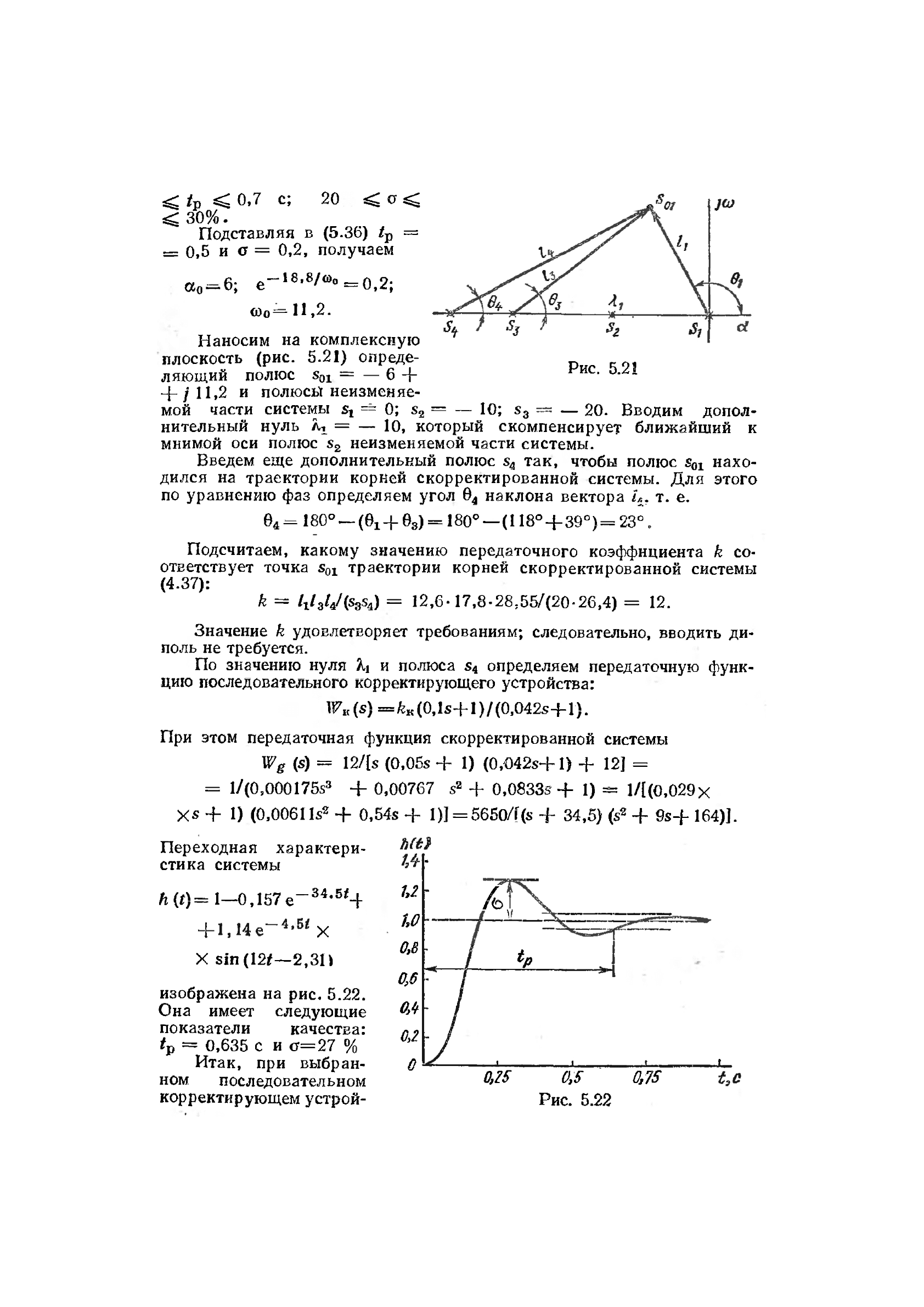
10; s

Рис. 5.21

— 20. Вводим допол-

Наносим на комплексную

плоскость (рис. 5.21) опреде-

ляющий полюс s

= — 6 +

+ /11,2 и полюськ неизменяе-

мой части системы s

== 0; s

нительный нуль = — 10, который скомпенсирует ближайший к

мнимой оси полюс s

неизменяемой части системы.

Введем еще дополнительный полюс s

так, чтобы полюс s

нахо-

дился на траектории корней скорректированной системы. Для этого

по уравнению фаз определяем угол в

наклона вектора т. е.

- i80°^-(e

) = iso°—о 18°+з9°)=23°.

Подсчитаем, какому значению передаточного коэффициента k со-

ответствует точка s

траектории корней скорректированной системы

(4.37):

k = MaVfesJ = 12,6.17,8-28,55/(20-26,4) = 12.

Значение k удовлетворяет требованиям; следовательно, вводить ди-

поль не требуется.

По значению нуля Я1 и полюса s

определяем передаточную функ-

цию последовательного корректирующего устройства:

(s) =M0,ls+I)/(0,O42s-f-l).

При этом передаточная функция скорректированной системы

(s) - 12/[s (0,05s + 1) (0,€42s+1) + 12] =

= 1/(0,000175s

+ 0,00767 s

+ 0,0833s + 1) l/[(0,029x

X* + 1) (0,0061 Is

+ 0,54s + 1)] = 5650/f(s + 34,5) (s

+ 9s+ 164)].

Переходная характери-

стика системы

h(t)= 1— 0,157 е~

X sin (12*—2,31 \

изображена на рис. 5.22.

Она имеет следующие

показатели качества:

*р = 0,635 с и 0=27 %

Итак, при выбран-

ном последовательном

корректирующем устрой-

0,8

0,6

0,2

ч>

А>

]

——1—

0,15 0,5 0,75

Рис. 5.22

стве система удовлетворяет требованиям. Однако следует заметить, что

показатели качества скорректированной системы заметно отличаются

от тех значений (fp = 0»5 с; о — 20 %), по которым производится рас-

чет. Зто объясняется недостаточным удалением полюсов s

и s

(см.

рис. 5.21) от определяющей пары комплексно-сопряженных полюсов.

В результате полюсы скорректированной системы имеют следующие

значения: s

= — 4,5 ± /12; s

— — 34,5 т. е. пара комплексно-

сопряженных' полюсов отличается от выбранной (определяющей) и на

динамику системы оказывает влияние полюс s

§ 5.7. Синтез корректирующих устройств

по логарифмическим амплитудно-частотным

характеристикам

Рассмотрим еще один метод синтеза корректирующих уст-

ройств, весьма детально разработанный и нашедший широкое

применение.

Пусть передаточная функция неизменяемой части системы

(s)^k

(s)/ls-oQ

(s)l

где Ro (s); Q

(s) — полиномы от s со свободным членом, рав-

ным единице; k

, v

— постоянные величины.

Потребуем, чтобы система была астатической v-ro порядка,

имела добротность k, перерегулирование не более а и время

регулирования не более t

. Такой комплекс требований весь-

ма часто предъявляют к следящим системам. Значения по-

рядка астатизма v и добротности k выбирают, исходя из не-

обходимой точности регулирования в установившихся режи-

мах. Выбором показателей качества переходной характери-

стики — перерегулирования о и времени регулирования —

гарантируются необходимые быстродействие и динамическая

точность системы.

В некоторых случаях необходимо, чтобы при начальном

рассогласовании g

ускорение регулируемой координаты ке

превышало некоторого допустимого значения w. Такое огра-

ничение необходимо, например, в механических системах,

когда регулируемой координатой является перемещение. Пре-

дупреждается появление в регулируемом объекте и в исполни-

тельном элементе недопустимых перегрузок (механических,

электрических и т. п.).

Легко установить, что если порядок астатизма v

неизме-

няемой части системы меньше v, то в усилитёльно-преобразо-