Воронов А.А. Теория автоматического управления. Часть первая

Подождите немного. Документ загружается.

рации над ними с точностью, превосходящей рабочую точность

ЭВМ. Такой способ резко увеличивает объем потребного ма-

шинного времени и загружает память. В "задачах машинного

проектирования систем управления этот способ имеет огра-

ниченное применение.

Значительный эффект достигается за счет применения но-

вых вычислительных методов. Изменение вычислительной схе-

мы или использование нового подхода часто дает возможность

принципиально решить задачу на ЭВМ. Характерна машинная

постановка фильтра Калмана в задачах управления и Навига-

ции. Последовательные вычисления в соответствии с урав-

нением Калмана не приводят к положительно-полуопределен-

ной матрице ошибок. Причина неудачи кроется в операциях с

плохо обусловленными матрицами. Благоприятное изменение

вычислительной схемы позволило применить фильтр Калма-

на в космической системе «Аполлон». Сущность применения вы-

числительной схемы состояла в использовании метода «квад-

ратного корня матрицы». Использовался тот факт, что квадрат-

ный корень матрицы имеет разброс элементов в два раза мень-

ший, чем исходная матрица, и в этом проявляется как бы эф-

фект «удвоения» разрядной сетки.

Характерно получение передаточных функций по обычным

правилам преобразования структурных схем. В программе

должно быть предусмотрено раскрытие скобок, приведение

подобных членов и вычисление коэффициентов по убывающим

степеням производной. Некоторые коэффициенты элементар-

ных звеньев малы (как правило, всегда меньше единицы), по-

этому возникает опасность превращения в машинный нуль

старших коэффициентов характеристического уравнения.

При исследовании системы по уравнениям переменных со-

стояния часто возникает необходимость многократного по-

строения характеристического уравнения по исходным матри-

цам коэффициентов. Задача является частью «полной пробле-

мы собственных значений» и известна также как проблема по-

строения векового уравнения. Для того чтобы обойти много-

численные трудности, в течение десятилетий создавались раз-

личные приемы и методы, подробно изложенные в [151.

В задачах анализа и синтеза автоматических систем ча-

сто имеется определенная специфика, не позволяющая в пол-

ной мере воспользоваться стандартными программами, в ос-

нову которых положены известные методы. Одна группа ме-

тодов (А. М. Данилевского, А. Н. Крылова, Хессенберга, Са-

муэльсона и др.) чувствительна к частным особенностям ма-

трицы, например к «провалам», т. е. к вырождению (в смыс-

ле машинной точности) промежуточных определителей. Дру-

гая (методы, основанные на идее Леверье) не учитывает бы-

стрый рост погрешности на высоких порядках вследствие на-

копления ошибок округления, что ограничивает размерность

решаемых задач.

Прямые корневые методы, базирующиеся на построении

характеристического полинома, также чувствительны к на-

коплению ошибок округления. Применение их для исследова-

ния линейных систем порядка п ^ 20 показало, что накопле-

ние ошибок округления при построении характеристическо-

го полинома и последующее применение корневых методов

синтеза часто приводили к совершенно неправильным резуль-

татам. Устойчивые системы при определенных сочетаниях

параметров трактовались как неустойчивые и, наоборот, не-

устойчивые рассматривались как устойчивые. Многолетние

исследования показали, что при принятой длине разрядных

сеток отечественных ЦВМ граница надежной применимости

метода Ньютона (и его модификаций) составляет п ^ 20.

Если п> 20, результаты также получаются, но неопределен-

ность в результатах увеличивается. Они могут быть сильно ис-

кажены ошибками округления.

Особенно значительное накопление ошибки проявляется

при сильной связи корней полинома с его коэффициентами.

Показателен следующий простой пример 111]. Полином

— 4s

+ (6 — 49-10~

) s

— 4s + 1 отличается от полинома

(s — I)

только коэффициентом при s

. Характерно, что это

различие весьма незначительно, всего

49*

10-

. Однако если

все четыре корня второго полинома равны единице, то у пер-

вого полинома корни таковы: s

= 1,02681; s

~ 0,97389;

= 0,99965 ± 0,026455. Это значит, что сравнительно не-

значительное изменение коэффициентов (всего на 49-Ю-

)

приводит к существенному изменению корней (уже на 0,03).

При степенях полинома порядка 20 и выше может наступить

качественное искажение результатов.

Отметим еще одну особенность. Не все традиционные мето-

ды теории автоматического управления одинаково хорошо при-

способлены к машинной реализации. Затруднения встречают-

ся при реализации D-разбиения, частотных методов, формиро-

вании передаточных функций по структурным схемам.

Ценность D-разбиения как метода построения границ

области состоит в том, что метод не требует какой-либо на-

правленной процедуры для нахождения первой точки грани-

цы, т. е. является беспоисковым. Поиск, особенно в виде пол-

ного или частичного перебора точек плоскости параметров*

не всегда является целесообразным из-за затрат машинного

времени и отсутствия уверенности, что точка искомой области

может быть найдена, если область имеет малые размеры.

D-разбиение принципиально позволяе! сразу найти границы

области устойчивости в плоскости интересующих проектиров-

щика параметров. Однако свойства метода таковы, что помимо

действительных кривых, являющихся границами искомой об-

ласти, появляются «посторонние». «Посторонние» кривые

представляют собой границы областей на плоскости парамет-

ров, соответствующих одинаковому числу корней, расположен-

ных справа от мнимой оси. Например, одному корню в пра-

вой полуплоскости соответствует определенный диапазон из-

менения параметров на плоскости параметров. Два корня соот-

ветствуют другому диапазону изменения параметров, три кор-

ня — третьему и т. д. При больших порядках характеристиче-

ского полинома переплетение истинных и «посторонних» ли-

ний может принимать самые причудливые формы и выбор дей-

ствительных кривых среди большого количества линий оказы-

вается весьма трудной задачей при программировании. При

изменении со кривые могут претерпевать бесконечные разрывы

второго рода и ветви могут уходить в бесконечность.

При ручных расчетах для выделения искомой области слу-

жит графическая процедура штриховки по Неймарку. Суть ее

состоит в том, что при движении по кривой в сторону возраста-

ния со штриховку наносят слева, если определитель положите-

лен, и справа, если он отрицателен. При изменении со от —оо

до +оо получается двойная штриховка, так как при со = 0

изменяется знак определителя системы. Если определитель

обращается в нуль,то это приводит к бесконечному разрыву

второго рода. Особенности имеются и при штриховое особых

прямых. Более подробные сведения об этом можно найти в ра-

ботах [3, 8].

Штриховка затрудняет полноценную машинную реализа-

цию метода D-разбиения. Выбор действительной области среди

претендентов, к тому же часто разбросанных во всех квадран-

тах, заставляет привлекать алгебраические критерии, методы

непосредственного вычисления корней. Недостатком метода

является также его недостаточная универсальность. Варьируе-

мые параметры должны входить в коэффициенты характери-

стического уравнения линейно, возникают трудности при за-

дании расположения корней внутри трапеции, угла или других

фигур в левой полуплоскости. Все же метод D-разбиения явля-

ется единственным беспоисковым методом и может быть с ус-

пехом использован при построении областей устойчивости не

только в автоматических системах, но и в численных методах.

D-разбиение может также использоваться в качестве парал-

лельного или вспомогательного метода.

Метод D-разбиения можно существенно видоизменить, уп-

ростить и сделать более универсальным путем введения полино-

мов Чебышева. Полиномы Чебышева, обладая свойствами как

гармонических, так и-ортогональных функций, являются уни-

кальными и как будто специально созданы для применения на

ЭВМ. Они, в частности, позволяют вести операции в веществен-

ной арифметике, что само по себе перспективно с точки зрения

возможной модификации некоторых традиционных методов,

ибо расчеты в комплексной арифметике увеличивают объем вы-

числений в четыре раза.

Другой пример — автоматизация построения передаточных

функций в сложных структурных схемах. Наиболее распро-

страненные алгоритмические языки приспособлены для опе-

раций с числами и не вполне подходят для обработки буквенной

информации. Новые вычислительные методы, создаваемые на

основе графов и структурных чисел, позволяют обойти эти

трудности и значительно уменьшить ошибки округления.

Машинная реализация JI4X имеет ряд особенностей. Полу-

чение амплитудной характеристики не вызывает затруднений.

Трудность кроется в вычислении фазовой характеристики, кото-

рая в общем случае находится не только в первом квадранте,

т. е. является разрывной. Видоизменение метода частотных

характеристик применительно к машинной реализации приво-

дит к предотвращению ложных скачков фазы и в целом повы-

шает информационную ценность метода частотных характе-

ристик. Например, в перспективе оказывается целесообразным

строить новые частотные характеристики — изамплиты (ли-

нии равных запасов устойчивости по амплитуде) и изофазы

(линии равных запасов устойчивости по фазе). Таким образом,

машинная ориентация частотных методов приводит к появле-

нию новых способов машинного анализа и синтеза.

§ 6.2. Анализ устойчивости по уравнениям

переменных состояния

и по характеристическому уравнению

Пусть процессы в системе описываются уравнением (6Л).

Для того чтобы система (6.1) была асимптотически устойчива,

необходимо и достаточно, чтобы все собственные числа s

(i -= 1, п) матрицы А имели отрицательные действительные

части, т. е. лежали слева от мнимой оси плоскости комплекс-

ного переменного s.

Рассмотрим характеристическое уравнение

| А —sE | = 0, (6.4

где Е — единичная матрица.

Корни Si характеристического уравнения (6.4) являются

собственными числами матрицы А. Совокупность всех собствен-

ных чисел образует спектр матрицы А. Сумма элементов, стоя-

щих на главной диагонали, образует след матрицы А и обозна-

чается Sp А. След матрицы связан с ее собственными числами

соотношением

п п

Sp А = 2

ii = S

55=5

•

— 1

Раскрывая определитель |А — sE получим характери-

стическое уравнение

(-1 )"(s" + a

+ (6.6)

где а

— сумма всех диагональных миноров первого порядка,

равная следу Sp А; а

— сумма всех диагональных миноров

второго порядка матрицы А; а

— определитель матрицы А.

Анализ расположения всех собственных чисел- матрицы А

относительно, мнимой оси осуществляется по коэффициентам

уравнения (6.6) с помощью известных критериев.В системах

высокого порядка получение коэффициентов характеристиче-

ского уравнения часто связано с серьезными трудностями чис-

то вычислительного характера.

Число диагональных миноров &-го порядка матрицы А

равно

ft tt(n~l)... (n — fe+l) , ,

1л

—

1 11

—|

tC —

*f it»

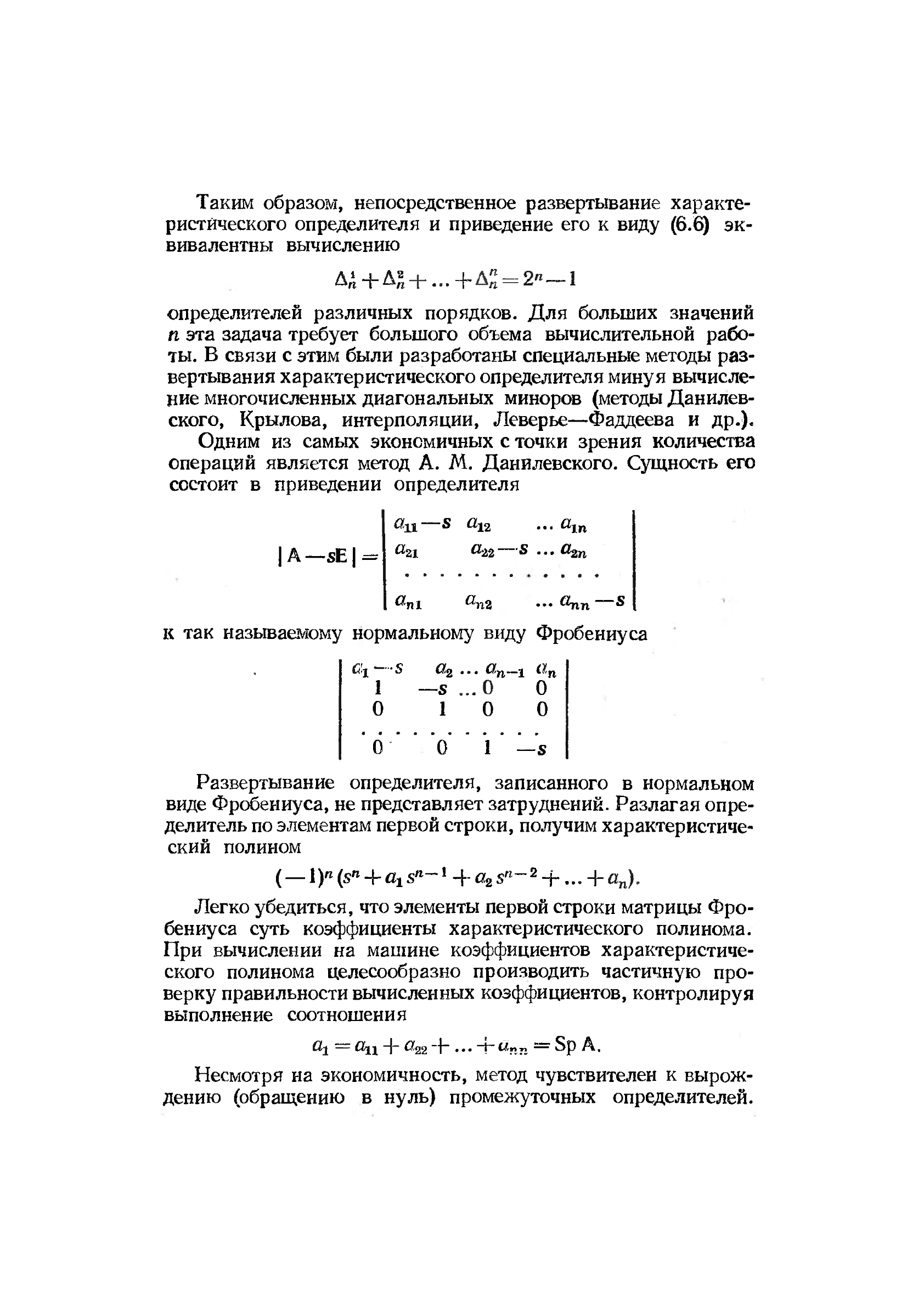
Таким образом, непосредственное развертывание характе-

ристического определителя и приведение его к виду (6.6) эк-

вивалентны вычислению

определителей различных порядков. Для больших значений

п эта задача требует большого объема вычислительной рабо-

ты. В связи с этим были разработаны специальные методы раз-

вертывания характеристического определителя минуя вычисле-

ние многочисленных диагональных миноров (методы Данилев-

ского, Крылова, интерполяции, Леверье—Фаддеева и др.)*

Одним из самых экономичных с точки зрения количества

операций является метод А. М. Данилевского. Сущность его

состоит в приведении определителя

| А—sE |

—

$21 $22

• •

$1и

•S ... &2

а,

а»

п1

n2 ®пп

к так называемому нормальному виду Фробениуса

i—

... О

—s 0

0 1

0 0

0 1 -

-S

Развертывание определителя, записанного в нормальном

виде Фробениуса, не представляет затруднений. Разлагая опре-

делитель

по

элементам первой строки, получим характеристиче-

ский полином

(_\)п

(

+ й1

n- i

n-2

Легко убедиться, что элементы первой строки матрицы Фро-

бениуса суть коэффициенты характеристического полинома.

При вычислении на машине коэффициентов характеристиче-

ского полинома целесообразно производить частичную про-

верку правильности вычисленных коэффициентов, контролируя

выполнение соотношения

<hx

+ +... = Sp А.

Несмотря на экономичность, метод чувствителен к вырож-

дению (обращению в нуль) промежуточных определителей.

Метод, предложенный А. Н. Крыловым, заключается в пред-

варительном преобразовании уравнения

в эквивалентное ему

D(s)

<р

(5) = | А —sE |

Ьи-

Ь-i

...

b-i

S ^12

- • •

Ьъъ . • .

'2п

пП

развертывание которого по степеням s осуществляется значи-

тельно проще, так как определитель можно разлагать по ми-

норам первого столбца. Метод чувствителен к вырождению

определителей и имеет меньшую точность вычисленных коэф-

фициентов.

Нечувствителен к вырождению определителей метод Леве-

рье—Фаддеева. Расчетная схема состоит в построении последо-

вательности

А^

-—

A; Gj

—

Sp Ajj Cj = Aj —E;

AC^; &2

= Sp А?у2;

—E;

A„ AC

^; a

= Sp A Jn\ C

- A

—a

Полученные величины a

представляют собой ко-

эффициенты характеристического полинома

(s)

= (— 1)" | А

— sE

| - s" + а

+... + а

Отметим, что попутно с вычислением коэффициентов харак-

теристического полинома может быть построена обратная ма-

трица А-

= C

_i/a

. Практически метод сводится к га-

кратному перемножению матриц порядка п. Число операций

умножения составляет около (rt — 1) и

При реализации этого метода на ЦВМ в случае операций

с матрицами высокого порядка может происходить перепол-

нение разрядной сетки, что вызывает необходимость введения

масштабирования; при вычислении .последовательности ма-

триц С

происходит накопление ошибки при округлениях, ко-

торое с увеличением порядка матрицы увеличивается, так как

происходит пропадание последних значащих цифр ввиду вы-

читания очень близких друг к другу величин, Это приводит к

тому, что при больших порядках матрицы А коэффициенты ха-

рактеристического полинома оказываются вычисленными с

пониженной степенью точности. Накопление ошибки начи-

нается с 7—8-го порядка и в дальнейшем увеличивается с ро-

стом п.

Если задана структурная схема системы и имеются переда-

точные функции отдельных звеньев, то определение передаточ-

ной функции ведется по обычным правилам структурных пре-

образований схем и построение характеристического полинома

не таит в себе принципиальных трудностей. Однако при руч-

ных расчетах это связано с утомительными выкладками, кото-

рые могут являться источником ошибок. При постановке зада-

чи на ЦВМ передаточные функции отдельных звеньев представ-

ляются полиномами не выше второго порядка. Характеристи-

ческий полином системы может быть записан в виде

P(s)= П (A

sl + B

s+Cj.

Программа должна предусматривать раскрытие скобок и

приведение подобных членов.

Перспективно построение передаточной функции с помощью

топологических методов.

Реализация на ЦВМ этих методов излагается в специальной

литературе.

В настоящее время для оценки расположения корней ха-

рактеристического уравнения относительно мнимой оси су-

ществуют критерии Рауса, Гурвица, Льенара—Шипара, Ми-

хайлова, Найквиста, методы непосредственного вычисления

корней (Ньютона, Мюллера, Берстоу). Для анализа устойчи-

вости импульсных систем используется критерий Шура—

Кона. Все перечисленные критерии опираются на знание ко-

эффициентов характеристического полинома.

Машинная реализация и сопоставление критериев показа-

ли, что наиболее простой, удобной в реализации и надежной

является вычислительная схема Рауса. Критерий позволяет

исследовать систему с учетом любой заданной степени устойчи-

вости

т|.

При этом возникает задача формирования коэффициен-

тов смещенного характеристического уравнения

(s—tj)

+ а

(s—

+... + а

=!0.

Относительно новых коэффициентов уравнение записыва-

ется в виде

- a

+ a

+... + а

Коэффициенты а

, а

...

суть

i —

где k — номер коэффициента; С — число сочетаний по к — i

из п — i.

Формула для а

может быть представлена так:

( W

ft0 (k-i)\(n~k)\

•

Отрицательным значениям величины г\ соответствует сме-

щение прямой s

—

г] вправо, а положительным — влево.

Рассмотрим, например, характеристическое уравнение трет

тьего порядка. Сместим его влево на величину степени устой*

чивости ц. Вычислим коэффициенты а

Имеем:

^а

; = — Зя

?На

= За

rf—2а

г\ + а

;

«з = —«о'П

^ ^rj + а

Если характеристическое уравнение записать в виде

1 — 0

то коэффициенты смещенного уравнения вычисляются по видск

измененной формуле

J (—1У-*n*-*CSZ2,

где Сп — число сочетаний из п по т (i — п

п — 1, 0).

Отметим, что в некоторых задачах, например при направ-

ленном выходе в область устойчивости* критерий Рауса и с*

пользовать затруднительно, так как он не позволяет ввести

количественную меру. (Это, впрочем, относится и к другим

критериям, в которых используется принцип ДА—НЕТ).

В качестве такой количественной "меры, например, может быть

использована вещественная часть ближайшего к мнимой оси

собственного числа Res

max

. Величина Res

ma?

является не-

прерывной, хотя и негладкой, функцией параметров. Если

задана область допустимых значений параметров, то возмож-

но из неустойчивой точки направленно выйти на границу об-

ласти устойчивости. Применение критерия Рауса в такой си-

туации приводит к тактике прямого перебора, хотя в силу эко-

номичности критерия это часто оказывается оправданным

§ 6.3. Функционально-преобразованные матрицы

и их применение. Критерий В. И. Зубова

Рассмотрим систему

x = Ax + F(*), (6.7

где А — матрица коэффициентов размерности п X п; F

(t)

—

вектор-функция внешних воздействий (п X I).

Пусть на плоскости комплексного переменного з задана

некоторая область D, соответствующая различным случаям-

расположения спектра s

исходной матрицы коэффициентов А

системы (6.7). Область D может быть произвольной частью

плоскости s, в том числе левой полуплоскостью или некоторой

заданной частью ее. Обозначим совокупность всех матриц

порядка п

спектр которых находится внутри области D,

через A

С другой стороны, пусть на-плоскости комплексного пере-

менного р задан круг радиуса г с центром в начале координат.

Обозначим через В

совокупность всех матриц порядка п,

спектр которых р* находится внутри круга радиуса

Ipil < r

i = i, п.

Допустим, что существует оператор L, устанавливающий

взаимно однозначное соответствие двух множеств: A

и В

Если А £ A

, то оператор L (А) от матрицы А есть такая ма-

трица порядка п

что L (А) £ В