Воронов А.А. Теория автоматического управления. Часть первая

Подождите немного. Документ загружается.

Далее имеем

(2k -}-2)

2И

- exp

[AA

(2k -f

2)]

+ f exp {A

[(2k

+ 2) x

—T]}F(T)rfT,

или

(2k+2)h \

4h + j exp [A (2kh

—T)1

F (т) dr 1. (6.40)

2 kh J

P (2AA)

Применим к интегралу в правой части выражения (6.40)

формулу Симпсона. Тогда

(2fe-f 2)h

j exp

[А

(2kh

—т)1

(т)

dr - (ft/3) {exp (—2Ah) x

2 kh

X F

[(2k

+ 2)A] + F

(2kh)

4 4 exp (—

Aft)

[(2k

+ 1)ft]}.

Выполнив необходимые преобразования, получим рекур-

рентную формулу

2№

= exp (2

Aft)

2fe

+ (hi3) F

(2kh)]

4- (4/3) h exp (AA) x

X Fl(2k + 1)A] + (A/3)F[(2k 4-2)A], ft-0, 1, 2, 3, ....

С учетом функционально-преобразованной матрицы окон-

чательное выражение алгоритма для построения переходных

процессов имеет вид

Хаы-2 - Dm [X

2fe

+ (А/3) F (2kh)\ + D

(4/3) AF [(2k 4 1)

+ (A/3)F[(2ft+ 2)A], ft-0, 1, 2, ....

Порядок точности при параболической аппроксимации инте-

грала пропорционален 0 (ft

), что соответствует по точности

интегрированию с использованием функционально-преобра-

зованной матрицы D

Способ вычисления интеграла вносит систематические ошиб-

ки в значение вектора x

. Более подробные способы исследова-

ния точности приводятся в работе ]6]. Изложенные алгоритмы

распространяются на построение переходных процессов в ли-

нейных нестационарных системах.

Можно выбрать максимальный шаг построения процессов

по ошибке вычисления вектора x

на k-ш шаге. Обозначим эту

ошибку через 6

. Тогда величина шага будет равна

m-и r—z —

— I/ + l)f,

I %ах

у k

где m — число, определяющее структуру функционально-пре-

образованной матрицы

~ Е +

АЛ

+ А

#72! +... + А

/т!

При т =

величина шага Л == — | f

;

I %nax

V к

е.

. , V120 , Г^Ъь

при т^Л Л = — I/

I «шах I

У к

где [s

max

— наибольшее по модулю собственное число матри-

цы А.

Максимальное время, в течение которого ошибка не будет

превосходить заданной величины, равно

h(m +1)1

I Smax

Пример 6.4. Проиллюстрируем на простом примере изложенные

способы построения переходных процессов. Все расчеты легко выпол-

няются на ручных калькуляторах.

Рассмотрим систему дифференциальных уравнений

х = Ах + F (/),

где

- -з 4

. Вектор-функция внешних воздействий F (/) имеет разрывной ха-

рактер, причем в точках разрыва она меняет знак. Ее аналитичес-

кое выражение имеет вид

1/2/ —

при 0 < t < 1;

— ~]/

2t—

при 1<*<2;

t—4 при 2< t < 3;

1 при 3 < t < оо.

Вектор начальных условий

Г П

Шаг построения процессов выбираем из соотношения h = !//?,'

где R — радиус круга, в котором находятся все собственные числа мат-

рицы А. Величина R может быть приближенно выбрана по норме || А

R>c\\ A||

где с — множитель, округляющий значение {| А

{{

до ближайшего цело-

го десятка (или сотни). Большие значения R приводят к малому шагу.

Найдем иорму:

Н А ||| = шах 2 l«z/I-max[l; 6] 6.

i /~i

Полагая R = 10, получим h = 0,1.

Построим переходный процесс по формуле (6.34):

+hF

(kh)]

=0, 1,2, 3, ...

В качества D

примем D

[

0,9864259 0,08596257

—о]2578875 О.!**»}

Значения функции F(f) можно вычислить по формулам с любой точ-

ностью. Для иллюстрации примем приближенно:

Г0

при F (0)

при ^0,1 F(A) = F(0

10,42J'

при /=0,2 F (2Л) = F (0,2) =

при /=0,3 F (ЗА)

—

F (0,3) =

при /=0,4 F(4ft)=F(0,4)

0,6

.б]'

[0,71]

|0,71Г

Р-

На первом шаге в момент времени 0,1 с получим следующие

значения переменных:

= [хо+0,IF (0)1 =

,029406

Г 0,9864259 0,08596251 ( Г1 7

Г°]

L—0,2578875 0,7285375J U0,5j

+ 1

[oj ) [о,

106382

На втором шаге в момент времени t — 0,2 с имеем

-D

1X^0,1^(0,1)1-

Г 0,9864259 0,08596251 г Г1,0294061 Г

1\_Л 1»

069616

М,2578875 0,7285375] ( |0,106382J

[о,42] f ^ [—0

1682012J

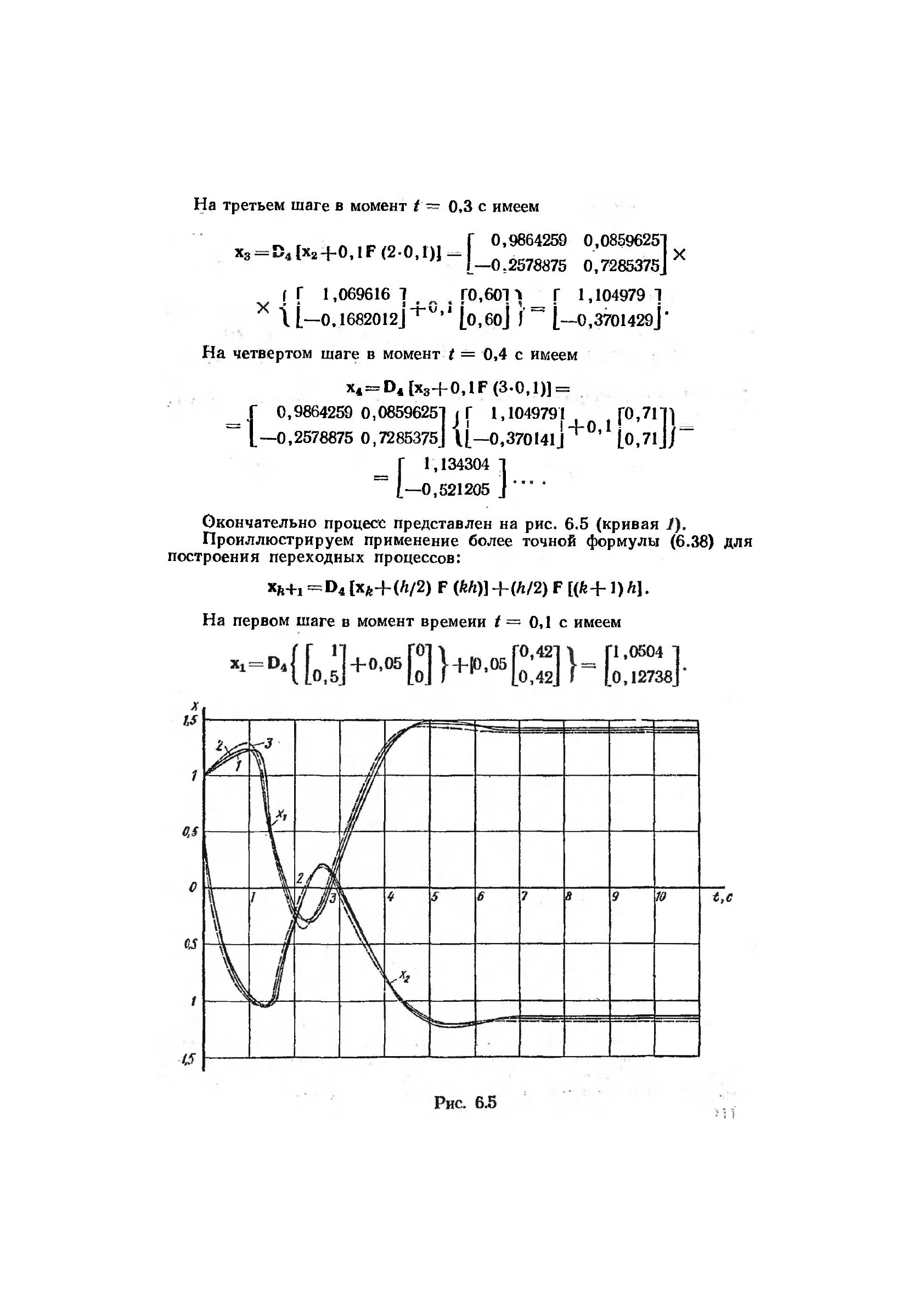
На третьем шаге в момент t ~ 0,3 с имеем

гч г .

л л

Г 0,9864259 0,08596251

з —t

2+0,!F (2-0,1)1 — I х

т п 257Ш5 0,7285375J

Г Г 1,069616 1 ГО,601Л Г 1,104979 1

\ 1—0,1662012]"^ ' [o,6oJ J [—0,3701429J"

На четвертом шаге в момент t = 0,4 с имеем

= D

+0,IF (3-0,1)] =

_ Г 0,9864259 0,08596251 J Г I,1049791 Г°»

~ \—0,2578875 0,7285375J Ц-0,370141J

+ 1

[0,71 \Г

_ Г 1,134304 1

" [—0,521205 J

Окончательно процесс представлен на рис. 6.5 (кривая

Проиллюстрируем применение более точной формулы (6.38) для

построения переходных процессов:

ХМ-1 [Х*+(*/2) F {kh)]+(h/2) F [(k+ \)h\.

На первом шаге в момент времени t = 0,1 с имеем

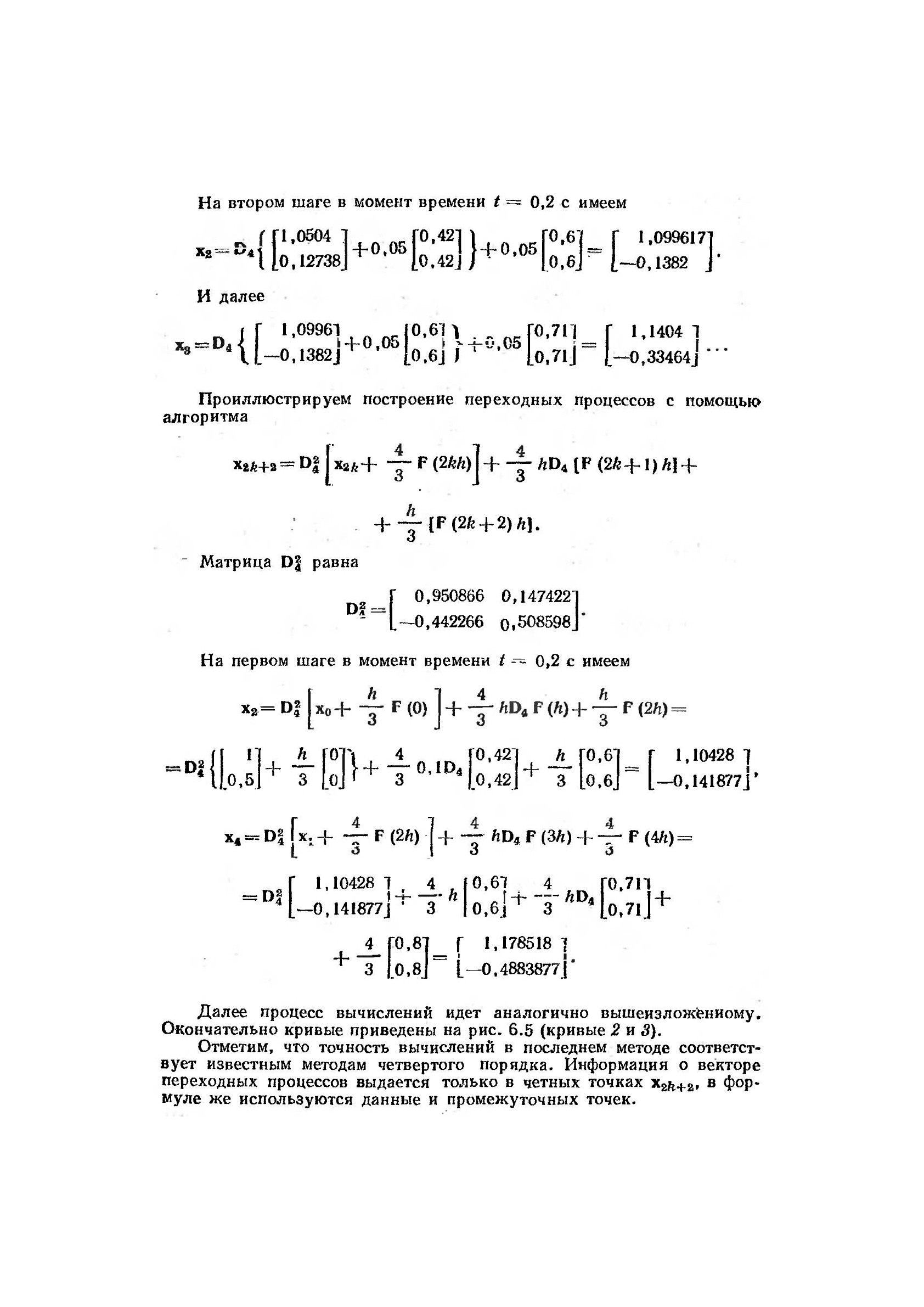
На втором шаге в момент времени t = 0,2 с имеем

0504

1+0.05Г

! }+o,o5[°-

]= Г

099617

2 4

1 [о,

12738

[o,42J / ' |o,6j [-0,1382 J'

И далее

1,09961 „ _ 10,61 ^ ГО,7Г| Г 1,1404 1

—0,1382j"'

(o,6j J ' [о]71J

[—0*33464j

Проиллюстрируем построение переходных процессов с помощью

алгоритма

хщ-,«D{ jx

*+ — F (2M)J+ -у /*D

IF (2k+\)h\ +

Матрица DJ равна

-j[F(2fe

h].

Г 0,950866 0,1474221

[—0,442266 о,50859в]

На первом шаге в момент времени t — 0,2 с имеем

= Df

ofl П

r^Tl 4 ГО,421 h Г0,61 Г 1,10428 1

°ЧМ

Т U\\

T°-

«M+ TkeJ-

[—о]

141877J*

= D| L+ F

(2ft)

j+ -j

ftD«

(ЗЛ)

F (4ft) =

„ Г 1,10428 1,4 , 10,61 4 Г0.7П

[•—0,14I877J 3* 10,6j ~3~ [o,7lJ^~

4 f0,81 Г 1,178518 1

[0,8] Г 1,

LO.eJ L-0.

з 1.0,8j L—0,4883877J

Далее процесс вычислений идет аналогично вышеизложенному.

Окончательно кривые приведены на рис. 6.5 (кривые 2 и S).

Отметим, что точность вычислений в последнем методе соответст-

вует известным методам четвертого порядка. Информация о векторе

переходных процессов выдается только в четных точках х

Ь+2» в фор-

муле же используются данные и промежуточных точек.

§ 6.6. Векторный способ построения переходных

процессов в нелинейных системах

Пусть динамика автоматической системы описывается век-

торным нелинейным дифференциальным уравнением

х " f (х, /). (6.41)

Представим систему (6.41) в виде линейной и нелинейной

частей:

Ax + F(x, t). (6.42)

Пусть спектр матрицы А системы (6.42) расположен в ле-

вой полуплоскости. Точное решение системы (6.42) можно пред-

ставить в аналитическом виде:

х (0 - ехр (АО х

+ J ехр [A {t—

т)]

F [х (т), т] dx. (6.43)

При интегрировании с шагом h получим рекуррентную фор-

мулу

(НИ

к+1

= ехр (АЛ) {x

f ехр [A (kh

— т)]

XF[x(t), x]dx}, /2—0, 1, 2, ....

Вычислим интеграл в правой части рекуррентной формулы.

Используя правило прямоугольников и принимая на левом

конце т = kh, получим

(A-f 1)

j* ехр (A (kh

— т)]

F [х (т), т] dx = hF (x

kh).

Таким образом, имеем

fe+1

- ехр

(АЛ)

+ hF (x

, kh)]. (6.44)

Для повышения точности построения переходных процес-

сов применим правило прямоугольников не ко всей подынте-

гральной функции, а только к функции F [х (т), т], т. е. бу-

дем считать, что на длине одного шага на промежутке [kh,

(k + 1) Л]

F[x(t), т] = F (x

, kh).

В этом случае

(k+i)h

h+1

= ехр (AЛ) |x

+ F (x

, kh) J ехр [A (kh— т)] dx

[ kh

Далее,

<&-H)ft h

J ехр IA (kh —

T) dx]

= j exp(—Ax) dx

kh О

« —А-

[ехр (—АЛ) — E] = A-

[E - exp

(—Ah)].

Матричную экспоненту представим в виде

/ лгл с А

f (А^)

\Щ

ехр(— Ah) = Е — Ah +

' -j-....

Имеем

<Ar-f 1) h

ехр [A

(kh)

—т]

dx - А-

(АЙ — J^L -}< —... V

t) \ 21 31 /

Вынося Ah за скобку и учитывая, что A~*A « Е, получим

(£+1) h

С ехр [A

(Aft

—

т)]

dt = ft ^Е + —••• j.

Итак, имеем следующий алгоритм для построения переход-

ных процессов:

ft+1

= ехр (АЛ) jx

+ h(е —£ + -... JF<х

) ].

(6.45)

Обозначим

Q(Ah.) — Е

—+Ш. (6.46)

Формулу (6.45) можно записать в виде

= ехр (АЛ) [x

(Ah) F (x

, kh)]. (6.47)

Более точные формулы для вычисления х

к+1

можно получить,

используя большое число членов ряда (6.46). В качестве

ехр (АЛ) можно подставлять функционально-преобразованные,

матрицы D

...» D

или использовать другие способы прибли-

жения. Отметим, что алгоритм с самого начала предполага-

ет расположение спектра матрицы А слева от мнимой оси.

Выбор шага в изложенном способе построения переходных

процессов легко осуществляется по линейной части системы.

В случае сильного влияния нелинейностей выбор шага осуще-

ствляется другими методами. Подробное их рассмотрение выхо-

дит за рамки данного учебника.

Изложенный векторный способ может быть распростра-

нен на построение переходных процессов в нелинейных неста-

ционарных системах.

Пример 6.5. Для иллюстрации рассмотрим пример. Пусть нели-

нейная система описывается уравнениями

ЗА'2

Xi х%

+ х

;

= —

—

2*2+5^ +0,5*}-f-jtg.

Начальные условия % (0) = I; х

(0) — 0,5. Требуется построить

процессы в системе, удовлетворяющие заданным начальным условиям.

Представим систему в виде линейной и нелинейной частей:

х —Ax+F (х),

где

д_

0 3

(x)4*

]

[-5 -ЯГ l5**+0

5*J + *8J

Используем функционально-преобразованную матрицу D

. В ка-

честве Q выберем матрицу Q

. Шаг примем равным 0,1, что соответст-

вует выбору его по линейной части. В общем случае такой выбор не

может быть универсальным и зависит от вида нелинейной функции.

Алгоритм построения процессов имеет вид

+ ftQ

F fx*, kh)].

Построим матрицы D

и Q

(Aft)

01 Г

0.3] 1 Г—0,15 —0,061

D^E+.AA+V- - [о ,]+ —0,5 -0,

J+ Т[ 0,1 -O.nJ "

Г 0,925 0,2? 1

"""

—0,45 0,745J'

[1 01 ±

* 0

0,3] 1

|о 1J 2

.—0,5 - 0,25

,151

Л Г

-0,15

Вектор нелинейной части для каждого шага пересчитываете я. Для

момента времени t = h = 0,1 с вектор F (x

, kh) равен

Г 1-0,5 -fl

1 П.5 1

F (Хо) _

[5.10,5 + 0,5

• 12

+ 0.52 J ~ |3,25 J

0,5

-0,5-

-1

"IS

-2

9,2

№

0,6 0,8

1 jjT

1Л

Рис. 6.6

Для момента времени / = 0,1 с имеем

= х (0,1) - D

[*о

+ (Е—0,5АЛ) hF (х

)] =

0,925 0,27 1 |Г i 1 Г1 —0,15"| Г1,5 П

0,45 0,745J |L 0,5 J '

|о,25

1,1

JU,25j/

1,255137]

0.1711 J'

-T

Для момента времени / — 2Л == 0,2 с вектор нелинейной части

F (х, kh) равен

F(x*

'25

1,7901221

J "

1,890728J

1,255137-0,1711Н- 1,255137

,255137-0,1711+0,5 1,255137

4-0

Решение в момент t = 0,2 с имеет вид

—

х (0,2) = D

[Х

+ (Е —0,5А/г) h? (x

Ш] =

Г 0,925 0,27 I JT1,2551371 ^ Г1 —0,151 Г1,79012211

—0,45 0,745j {[0,1711 ]

' |0,25 1,1 J И ,890728JJ

1,4147871

0,316849j

далее х

Г 1,3592541 Г О,

"[-1,01481 J'

L-1.

0,8586151

7938!7j'

Дальнейший ход вычислений представлен на графике (рис. 6,6),

§ 6-7. Стандартные численные методы

интегрирования

Многие важные задачи анализа и синтеза автоматических

систем решаются нахождением кривых переходных процессов

(выявление интервала устойчивого функционирования асимп-

тотически неустойчивой системы, оптимальный синтез). Постро-

ить переходный процесс—это значит проинтегрировать диф-

ференциальное уравнение и получить решение, удовлетворяю-

щее заданным начальным условиям и возмущающим воздейст-

виям. Интегрирование может быть осуществлено различными

методами и выполняться с помощью аналоговых или цифровых

ЭВМ. Применение аналоговых ЭВМ позволяет интегрировать

-систему в ^реальном времени, хотя точность может быть недо-

статочной. При использовании цифровых ЭВМ интегрирование

осуществляется стандартными численными методами. К таким

методам относятся методы Эйлера, Рунге—Кутта, Адамса,

Хемминга, Гира.

Рассмотрим скалярное дифференциальное уравнение

х = / (х

(£

)

= х

Получить точное решение уравнения аналитическими мето-

дами удается весьма редко, поэтому ставится задача прибли-

зить точное решение с помощью вычислительных (численных)

методов.

Используются два обширных класса вычислительных мето-

дов. К первому относятся одношаговые (одноступенчатые) ме-

тоды. В этих методах для нахождения следующей точки х

к+1

кривой требуется информация только в одной предыдущей

точке (x

h> tfd'

К этому классу относится решение с помощью разложения в

ряд Тейлора, метод Эйлера, Эйлера—Коши, Рунге—Кутта.

Простейшим является метод Эйлера, основанный, на вычис-

лении точки х

посредством прямолинейной экстраполяции

из предыдущей точки х

. Если х (t) — гладкое решение урав-

нения (6.29), то оно имеет разложение в ряд Тейлора. Метод

Эйлера можно рассматривать как приближенное использова-