Воронов А.А. Теория автоматического управления. Часть первая
Подождите немного. Документ загружается.

а) д
-id
1
\ 1
г
W,
я,
w
2
W,
w
2
в)
в)
г
> .
JLt
у y
f
Рис. 2.18
Рис. 2.19
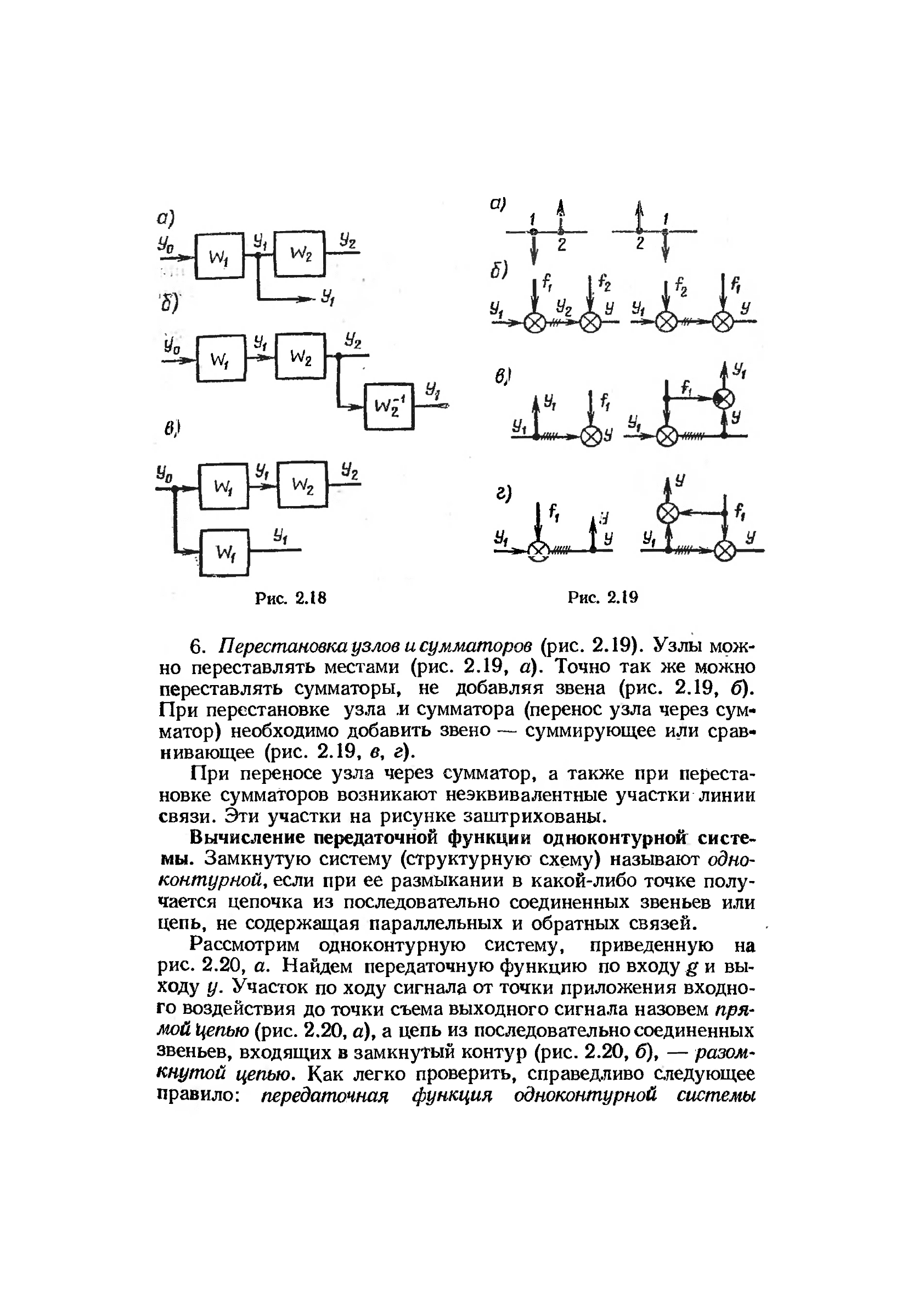
6.
Перестановка
у злое и сумматоров (рис. 2.19). Узлы мож-
но переставлять местами (рис. 2.19, а). Точно так же можно
переставлять сумматоры, не добавляя звена (рис. 2.19, б).
При перестановке узла и сумматора (перенос узла через сум-
матор) необходимо добавить звено — суммирующее или срав-
нивающее (рис. 2.19, в, г).
При переносе узла через сумматор, а также при переста-
новке сумматоров возникают неэквивалентные участки линии
связи. Эти участки на рисунке заштрихованы.
Вычисление передаточной функции одноконтурной: систе-
мы. Замкнутую систему (структурную схему) называют одно-
контурной, если при ее размыкании в какой-либо точке полу-
чается цепочка из последовательно соединенных звеньев или
цепь, не содержащая параллельных и обратных связей.
Рассмотрим одноконтурную систему, приведенную на
рис. 2.20, а. Найдем передаточную функцию по входу g и вы-
ходу у. Участок по ходу сигнала от точки приложения входно-
го воздействия до точки съема выходного сигнала назовем пря-
мой
Цепью
(рис. 2.20, а), а цепь из последовательно соединенных
звеньев, входящих в замкнутый контур (рис. 2.20, б), — разом-
кнутой цепью. Как легко проверить, справедливо следующее
правило: передаточная функция одноконтурной системы

Прямая цепь
5)
ХЬН ц
№
I
|—
w
2
-
У
>
|
Разомкнутая цепь
с отрицательной (положи-
тельной) обратной связью
равна передаточной функ-
ции прямой цепи, делен-
ной на единицу плюс (ми-
нус)
передаточная
функция
разомкнутой цепи:
w,
w
2
w
3
w,
w
2
w
3
W
x
W,
Рис. 2.20
1 ± W
l
W
2
W
8
I ± w
где W
u
— передаточная функция прямой цепи; W — переда-
точная функция разомкнутой цепи.
Сформулированное правило справедливо для любой одно-
контурной системы.
Вычисление передаточной функции многоконтурной сис-
темы. Замкнутую систему (структурную схему) называют
многоконтурной, если при ее размыкании получается цепь,
содержащая параллельные или обратные связи, или, иначе,
замкнутую систему называют многоконтурной, если она поми-
мо главной обратной связи содержит местные обратные или
параллельные связи. Говорят, что многоконтурная система
имеет перекрещивающиеся связи, если контур обратной или
параллельной связи охватывает участок цепи, содержащий
только начало или конец другой цепи обратной или параллель-
ной связи (рис. 2.21, а, б).
Для вычисления передаточной функции многоконтурной
системы необходимо прежде всего перестановкой и переносом
узлов и сумматоров освободиться от перекрещивающихся
связей. Затем, используя первые три правила преобразования
Рис.
2.72
структурных схем, преооразовать ее в одноконтурную систе-
му, передаточную функцию которой легко вычислить соглас-
но сформулированному выше правилу. Следует иметь в виду,
что при преобразовании структурной схемы нельзя перено-
сить сумматор через точку съема выходного сигнала, так как
при этом точка съема оказывается на неэквивалентном участке
линии связи.
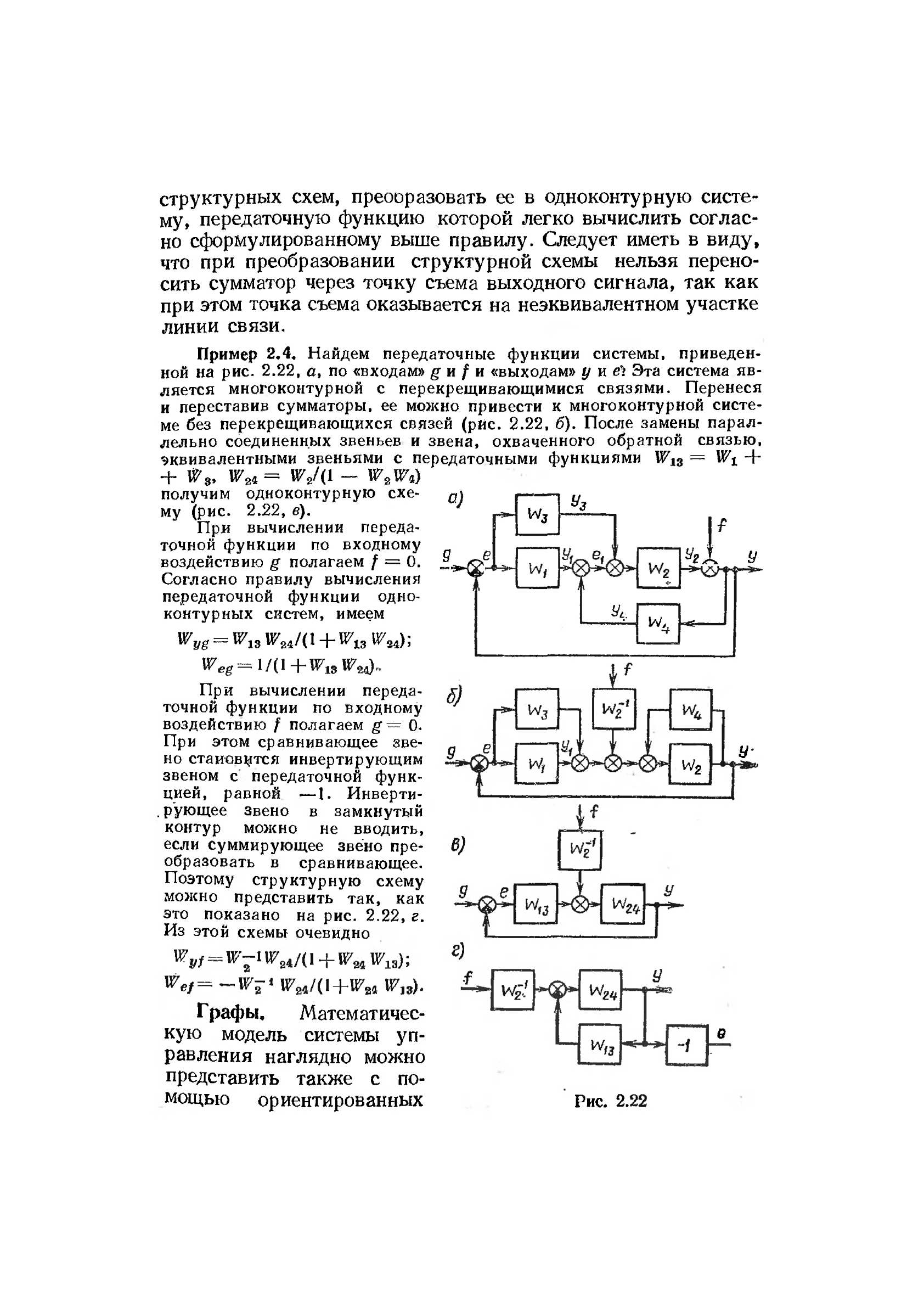
Пример 2.4. Найдем передаточные функции системы, приведен-
ной на рис. 2.22, а, по «входам» g и / и «выходам» у и Эта система яв-
ляется многоконтурной с перекрещивающимися связями. Перенеся
и переставив сумматоры, ее можно привести к многоконтурной систе-
ме без перекрещивающихся связей (рис. 2.22, б). После замены парал-
лельно соединенных звеньев и звена, охваченного обратной связью,
эквивалентными звеньями с передаточными функциями W
13
= W
t
~Ь
+ ir
3
, w^ = wj(i -
получим одноконтурную схе-
му (рис. 2.22, в).
При вычислении переда-
точной функции по входному
воздействию g полагаем / = 0.
Согласно правилу вычисления
передаточной функции одно-
контурных систем, имеем
w
yg =
W
19
W
2
J(
1
+ W
t3
Г
24
);
При вычислении переда-
точной функции по входному
воздействию / полагаем g — 0.
При этом сравнивающее зве-
но становится инвертирующим
звеном с передаточной функ-
цией, равной
— 1.
Инверти-
рующее звено в замкнутый
контур можно не вводить,
если суммирующее звено пре-
образовать в сравнивающее.
Поэтому структурную схему
можно представить так, как
это показано на рис. 2.22, г.
Из этой схемы очевидно
Графы, Математичес-
кую модель системы уп-
равления наглядно можно
представить также с по-
мощью ориентированных
•
w
3
Уз
•
w
3
0
?
е
1 i
у,
УгХ У
IV,
w
2
У
в
Рис.
2.73

графов. Графом называется [1] совокупность множества V то-
чек, называемых вершинами, и множества R простых (т. е.
самонепересекающихся) кривых, называемых ребрами, удов-
летворяющих следующим условиям: 1) каждое незамкнутое
ребро содержит ровно две тачки множества V, которые явля-
ются граничными точками ребра; 2) каждое замкнутое ребро
содержит только одну точку из V (граничные точки совпада-
ют); 3) ребра (кривые из множества R) не имеют общих точек,
за исключением точек из множества V.
На рисунке вершина изображается точкой или окружно-
стью. Граф обозначают одной буквой G или парой букв (V, /?),
где V — множество вершин, R — множество ребер графа.
Если множества V и R состоят из конечного числа элементов,
то граф (У, R) называется конечным. Граф Gi — (V
l9
Ri)>
который состоит из части вершин (Vi cz V) и части ребер
(/?! сI R) графа G = (V, /?), называется подграфом G. При
этом G называется подграфом G
x
. Если вершины v
h
и v
t
явля-
ются граничными точками ребра г, то говорят, что г инцидент-
но каждой из вершин v
k
и v
t
и, обратно, каждая из вершин
v
k
и v
t
инцидентна г. Граничные точки ребра г, очевидно,
можно определить как вершины, т. е. точки из множества V,
инцидентные г. Если ребро замкнуто, т. е. оно имеет только
одну граничную точку, то ребро называется петлей.
Если ребра ориентированы, т. е. на каждом ребре задано
направление, то граф называется ориентированным графом,
или орграфом. Ориентированные ребра называются дугами.
Поэтому ориентированный граф, или орграф, можно опре-
делить как совокупность множества V вершин и множества
D дуг, удовлетворяющих перечисленным выше трем услови-
ям. Вершина, являющаяся начальной граничной точкой ду-
ги d
u
называется ее начальной вершиной, а вершина, являю-
щаяся конечной граничной точкой дуги d
if
— ее конечной вер-
шиной.
Последовательность дуг^,..., d
n
(не обязательно разных),
для которой конечная вершина v% дуги d
t
является началь-
ной вершиной дуги d
i+1
, i = 1, п — 1, называется ориен-
тированным маршрутом (ормаршрутом). Ориентированный
маршрут называется замкнутым, если конечная вершина
v
n
дуги d
n
совпадает с начальной вершиной v
0
дуги d
x
. В против-
ном случае ормаршрут называется незамкнутым. Ормаршрут,
в котором нет повторяющихся дуг (все дуги разные), называет-
ся путем от вершины v
Q
к вершине v
n
, если он незамкнут, и
контуром (ориентированным циклом), если он замкнут. Если

а)
Jf
—
-НлН*-
Wt
w,
У 9
Рис. 2.23
все вершины v
0f
и
ъ
...
у
v
n
различны, то путь или контур назы-
вается простым (в случае контура v
0
и v
n
совпадают). Верши-
ны v
0
и v
n
будем называть соответственно начальной и конеч-
ной вершинами пути, а остальные вершины — промежуточ-
ными. Дуги й
л
и d
2
называются параллельными или строго
параллельными\ если они имеют общие начальную и конечную
вершины.
Граф системы управления представляет собой ориентиро-
ванный граф, который обладает следующими свойствами [3J:
1. Каждая дуга (ребро со стрелкой, указывающей направ-
ление распространения сигнала) изображает звено и характе-
ризуется оператором изображаемого ею звена. Поэтому можно
говорить о передаточной функции, дифференциальном уравне-
нии, частотных и временных функциях дуги.
2. Каждой вершине ставится в соответствие одна из пере-
менных. Если к вершине подходит (входит в нее) только одна
дуга, то соответствующая ей переменная равна выходной ве-
личине дуги (выходной величине изображаемого ею звена).
Если к вершине подходят несколько дуг, то соответствующая
ей переменная равна сумме выходных величин этих дуг. Вход-
ная величина дуги (входная величина изображаемого ею зве-
на) равна переменной вершины, из которой эта дуга исходит.
Если из вершины исходят несколько дуг, то входная величи-
на всех этих дуг одна и та же.
Граф системы управления легко построить по ее структур-
ной схеме. И наоборот, по графу системы управления нетруд-
но построить структурную схему. При построении графа сис-
темы управления по ее структурной схеме нужно исходную
схему (рис. 2.23, а) представить так, чтобы в сумматорах все
переменные складывались с положительным знаком (рис. 2.23,
б). Затем по последней схеме построить граф (рис. 2.23, в),
руководствуясь следующими правилами: 1) каждый сумматор
заменяется вершиной, которой ставится в соответствие выход-
ная переменная заменяемого сумматора; 2) каждое звено (пря-

а)
моугольник на структур-
н
°й схеме) заменяется ду-
гой с оператором, равным
W
z
Lj(/ оператору заменяемого
Рис. 2.24
«
звена; 3) каждой перемен-
ной (в том числе перемен-
ной, обозначающей внеш-
нее воздействие) соответ-
ствует своя вершина. Если нужно изобразить выход одной
из дуг (например, дуги с передаточной функцией W
t
на
рис. 2.24, a)
t
входящих в общую вершину, то следует ввести
дополнительную, конечную для этой дуги вершину и соеди-
нить эту вершину с исходной вершиной дугой с единичным
оператором (рис. 2.24, б).
На графе системы управления, как правило, для обозначе-
ния дуги и ее оператора, точно так же как и для обозначения
вершины и соответствующей ей переменной, будет использо-
ваться одна и та же переменная. И поэтому выражения «дуга
с оператором W» и «дуга W», а также выражения «вершиина,
соответствующая переменной х» и «вершина х» будут иметь
одинаковый смысл.
Формула Мейсона. Как нетрудно показать, параллельные
дуги (рис. 2.25, а) можно заменить одной дугой с передаточной
функцией, равной сумме передаточных функций исходных
дуг (рис. 2.25, б). Простой путь, если нет не принадлежащих
ему дуг, инцидентных его промежуточным вершинам, можно за-
менить дугой с передаточной, функцией, равной произведе-
нию передаточных функций Дуг этого пути. Так, например,
простой путь на рис. 2.25,
в
можно заменить дугой W = П
W%
(рис. 2.25, г). Простой путь на рис. 2.25, д заменить дугой нель-
зя, так как имеются не принадлежащие этому пути дуги
W
k
и W
lf
инцидентные его промежуточным вершинам.
Для упрощения графа и вычисления передаточной функции
системы управления по ее графу можно также воспользовать-
ся формулой Мейсона
п
-1
т
Здесь Wt — передаточная функция г-го простого пути от вер
шины g к вершине х
9
равная произведению передаточных функ

ций дуг, входящих в этот путь; т — общее число таких путей;
д — определитель графа;
Л =
1
-2 ^ + 2 2 +•....
/,/г /,/г,/
где в первой сумме IF
0J
-—передаточная функция /-го простого
контура, равная произведению передаточных функций входя-
щих в этот контур дуг, и суммирование производится по всем
простым контурам; во второй сумме W
0
jW
0k
— произведение
передаточных функций /-го и k-vo контуров и суммирование
производится по всем несоприкасающимся парам конту-
ров; в третьей сумме W
oj
W
ok
W
0[
— произведение передаточ-
ных функций /-го, 6-го и 1-го контуров и суммирование произ-
водится повеем несоприкасающимся тройкам контуров и т. д.;
д. — определитель подграфа, получающегося из исходного
графа при удалении дуг и вершин i-го простого пути, а также
всех дуг, инцидентных этим вершинам.
Два контура (пара контуров) называются несоприкасаю-
щимися, если они не имеют общих дуг и (или) общих вершин.
Тройка (четверка и т. д.) контуров называется несоприкасаю-
щейся, если любая пара контуров из этой тройки (четверки и
т. д.) является несоприкасающейся.
Подграф, получающийся при удалении дуг и вершин ка-
кого-либо простого пути, а также всех дуг, инцидентных уда-
ляемым вершинам, будем называть подграфом, соответствую-
щим этому простому пути.
Рис.
2.77
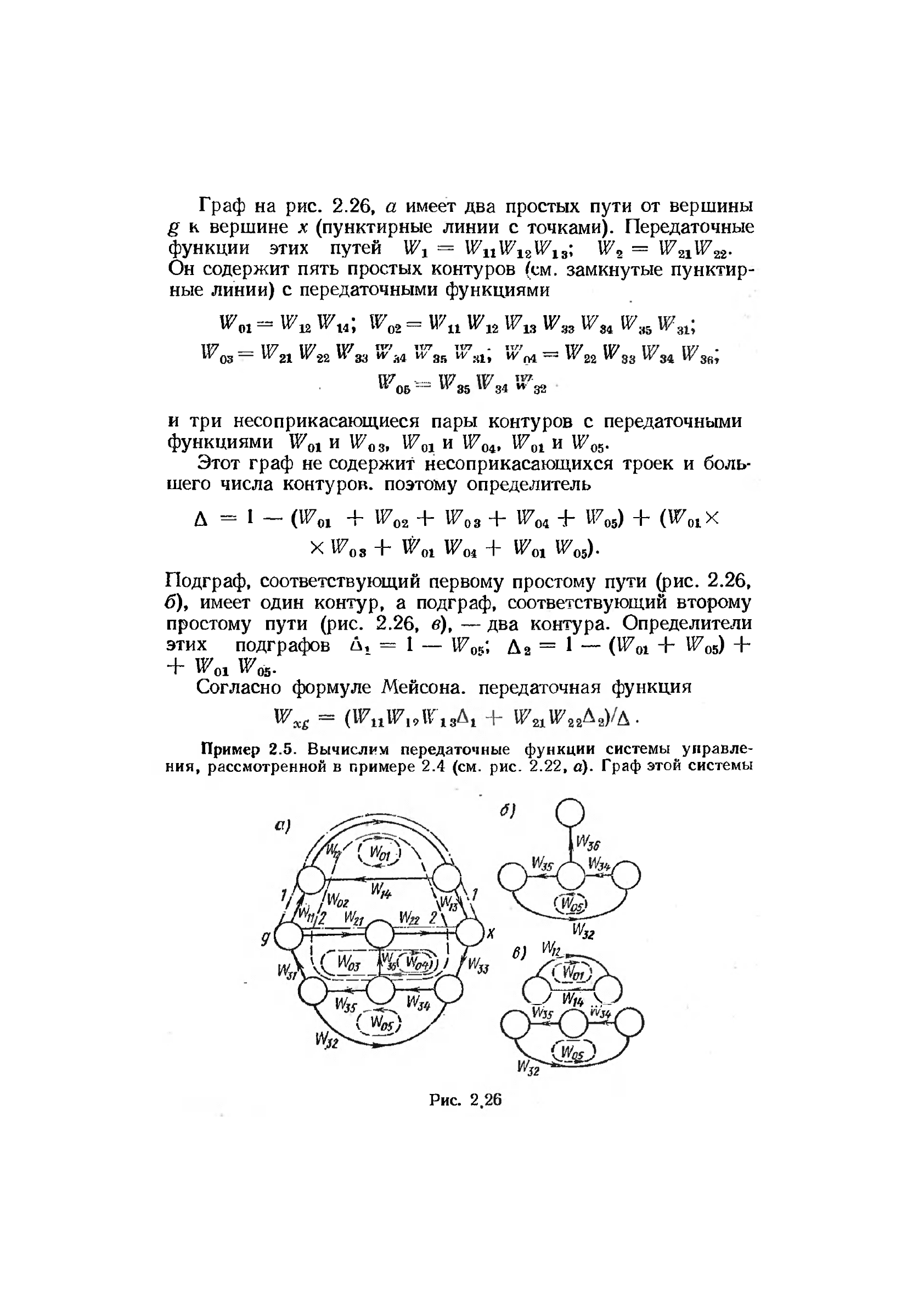
Граф на рис. 2.26, а имеет два простых пути от вершины
g к вершине х (пунктирные линии с точками). Передаточные
функции этих путей Ш
г
= W
n
W
12
W
l3
; W
2
= W
21
W
22
.
Он содержит пять простых контуров (см. замкнутые пунктир-
ные линии) с передаточными функциями
^01 Wn ^02 - U7
u
W
13
«7,3 Г
84
W.
Ab
= Wn ^22 ^33 - W
22
W
35
34
и
32
и три несоприкасающиеся пары контуров с передаточными
функциями W
0
i и W
Q3
, W
0
1 и U7
04
, l^oi
и
^os-
Этот граф не содержит несоприкасающихся троек и боль-
шего числа контуров, поэтому определитель
Л
1
(W
0l
+ W
b2
+ IF
03
+ 1^04 + И7вд) + (W
01
X
х IF
0S
+ 1Г
01
1^04 + W
0
i ^05)-
Подграф, соответствующий первому простому пути (рис. 2.26,
б), имеет один контур, а подграф, соответствующий второму
простому пути (рис. 2.26, в), — два контура. Определители
этих подграфов = I — W
ob
\ д
2
= 1 — (W
ol
+ IF
05
) +
+ W01 Wo
5
.
Согласно формуле Мейсона. передаточная функция
Пример 2.5. Вычислим передаточные функции системы управле-
ния, рассмотренной в примере 2.4 (см. рис. 2.22, а). Граф этой системы
К Щг
6) %
- % -
Рис.
2.78

Рис. 2.27
управления приведен на
рис. 2.27. Найдем передаточ-
ные функции W
yg
, Wyf и W
eg
.
От вершины g к вершине
у имеется два простых пути
с передаточными функциями
U7; = W
0
и?!
хг
%
- W
1
W
2
;
WiWiW*** w
2
w
3
.
Имеется три контура с пе-
редаточными функциями й^о!^
«и?! W
2
~
W
±
W
2
\
- w
2
w
4
; w
09
**w
9
wtw
b
=
—Vs.
. Несоприкасающихся пар и большего числа контуров граф не со-
держит. Поэтому его определитель
Д
-
I
+
U7
02
+
1Г
03
)
«
1
+ Г, W
2
+ w
2
w
3
.
Подграфы, соответствующие простым путям от вершины g к вер-
шине у, замкнутых контуров не содержат, и их определители А
х
== 1,
Л
2
= 1-
По формуле Мёйсона,
w
yg
=
(W;
+
W'
2
)fЛ
=
(W,
w
2
+w
2
w
3
)/(
1
+ w
x
w
2
- r
2
+w
2
w
3
).
От вершины f к вершине у ведет один простой путь — дуга W
e
.
Соответствующий этому пути подграф не имеет замкнутых контуров,
и его определитель Aj — I. Следовательно,
Wy
f
= WJA =
1
/
-(1
+
W
2
-
W
2
+
W
2
W
3
).
От вершины g к вершине
e,
ведет также один простой путь — дуга
W
0
. Соответствующий этому пути подграф имеет один контур с переда-
точной функцией
W
Q1
~ W
2
W
4
, и его определитель А
х
— 1 — W
01
=
=
1
— W
2
Wt.
Передаточная функция
W
eg
=
Го А
х
/Д
=
(1
-W
Q
Wjta
W
2
W
4
+
W
2
W
3
).
Дифференциальные уравнения. Зная передаточные функ-
ции системы, нетрудно записать ее дифференциальные уравне-
ния. Если система имеет одну управляемую величину, то для
ее полного описания достаточно иметь одно дифференциальное
уравнение, выражающее зависимость между выходной и вход-
ной величинами.
Автоматические системы с одной управляемой величиной
называют
одномерными.
В общем виде дифференциальное урав-
нение одномерной системы с двумя входными величинами, на-
пример задающим воздействием g и возмущающим воздейст-
вием /, можно записать как
(п) (п~
1)
(т)
<m— 1)
aoy +
a
iy +
---
+
a
ny = b
0
g + b
1
g + .. + b
m
g +
(t) (/-i)
+ C
0
f + C
1
f + ... + C
l
f.

Получим дифференциальное уравнение системы, рассмот-
ренной в примере 2.4 (рис. 2.22, а). Для нее
У = W
yg
g +
W
yf
f.
(2.53)
Это дифференциальное уравнение в символической форме,
связывающее выходную величину у с входными величинами.
Аналогично можно записать дифференциальное уравнение от-
носительно любой другой «выходной» величины. Исходя из
определения передаточной функции нетрудно перейти от урав
нения (2.53) к обычной «несимволической» форме записи.
Допустим, например, что = k
x
\ W
x
= kJ{p + 1);
W
b
- kjp\ U7
4
- kt. Тогда
W ~
Г
зР+1 . HP
2
+
P)
^ T\ p%-\-T
2
p+\ * *
vi
T\f + T
t
p+\
9
где k = l/(&
2
&
3
); 7\ — 7
2
= (1 + k
x
k
2
— k
2
kj /(k
2
k
3
);
T
3
= ki/k
3
.
Поэтому на основании (2.53)
п у -ы
2
у+у«г, ^+g+k а+/).
Частотные характеристики. При исследовании и проекти-
ровании автоматических систем обычно используют амплитуд-
но-фазовые и логарифмические частотные характеристики
разомкнутых систем. Передаточные функции W (s) разомкну-
тых одноконтурных, а иногда и многоконтурных систем мож-
но преобразовать к виду
№ (s) - П W
t
(s), (2.54)
I
где (s) — передаточные функции элементарных звеньев.
В этом случае модули и аргументы частотных пере-
даточных функций системы и звеньев А (со) =
|
W (/<о)|;
A
t
(co) = |U7, (/(о)|; ф (о>) = argU7 (/со); <р
4
(со) = arg
UPj
(/со)
в соответствии с правилом модулей и аргументов комплекс
ных чисел связаны между собой соотношениями
А
(со)
- П А,
(со);
(2.55)
1
п
ф(<й) •-= 2
Фг (<*>)•
— 1
(2.56)
