Воронов А.А. Теория автоматического управления. Часть первая

Подождите немного. Документ загружается.

где

Матрицы-столбцы х, и и f также называют векторами. Вектор

х называют

фазовым

вектором или вектором состояния, а его

координаты х

..., х

— фазовыми координатами. Вектор и

называют вектором управления или просто управлением, а его

координаты и

... и

— параметрами управления: Вектор

f называют вектором возмущения или просто возмущением, а

его /-я координата

—

/-м возмущением или /-:м возмущающим

воздействием.

Наряду с неоднородным уравнением (2.74) рассмотрим одно-

родное уравнение

х = Ах. (2.75)

Пусть х<

> - (4

) х<

> = (х<

)

— (л:

)

, х<^>)

образует п линейно независимых решений

этого уравнения. Любую такую систему называют фундамен-

тальной системой решений уравнения (2.75). Составим мат-

рицу, полагая в качестве ее i-ro столбца i e решение из фун-

даментальной системы:

[

(/)...*<"> (О •

(0"

(0 _

Эту матрицу называют фундаментальной матрицей урав-

нений (2.73) — (2.75). Если при t — t

фундаментальная мат-

рица обращается в единичную, то она называется нормиро-

ванной. Используя произвольную фундаментальную матрицу

Ф (t), нормированную (обозначим ее X (*, *

)) можно предста-

вить в виде

. Х(/,/

) = Ф (о Ф-

(д; х (/

, t

) = Е. (2.76)

С помощью нормированной фундаментальной матрицы ре-

шение неоднородного уравнения (2.74) при всех t их (t

) —

= х° можно представить в виде соотношения

х(0 =

(t,t

)х°+ f X (/, т) [Bu (т) +

С/.(т)]

dx, (2.77)

которое называется формулой Kotuu. В справедливости этой

формулы легко убедиться непосредственной подстановкой в

уравнение (2.74), воспользовавшись при этом матричным урав-

нением

Х(М

)-АХ(/, /

); Х(*

, У --= Е,

которое справедливо во всех t. Это уравнение следует из того,

что каждый столбец фундаментальной матрицы является ре-

шением (2.75).

Отметим ряд основных свойств нормированной фундамен-

тальной матрицы. Воспользовавшись (2.76), для любых t, £

и t

легко получить следующие равенства:

X (t, О X (С, у—X (/, /

); X"

(f,

) - X (t

, t).

Если матрица А постоянна, то фундаментальная матрица

X (t, t

) зависит только от разности t — t

и имеет вид X

— /

) — е

(t~t

)

Матричная функция е

(*-*о) называется

экспоненциальной матрицей или матричным экспоненциалом

и определяется суммой ряда

ЕА<* -1.) = Е + A (t—t

) + -J- A

(t — t

f +... +

Л——

A"(t —/

)" +... . (2.78)

п\

Рассмотрим уравнение, сопряженное (2.75): z = — A

Если Z (t, t

) -г нормированная фундаментальная матри-

ца этого уравнения, т. е.

dz(l

to)

— —A

z(t,/

); z(t

, g.-= e,

то формулу Коши можно представить в виде

(0 - Ъ

t) х (g + J

Z^ (f

0 [Bu (t) + Cf

(x)\

dx. (2.79)

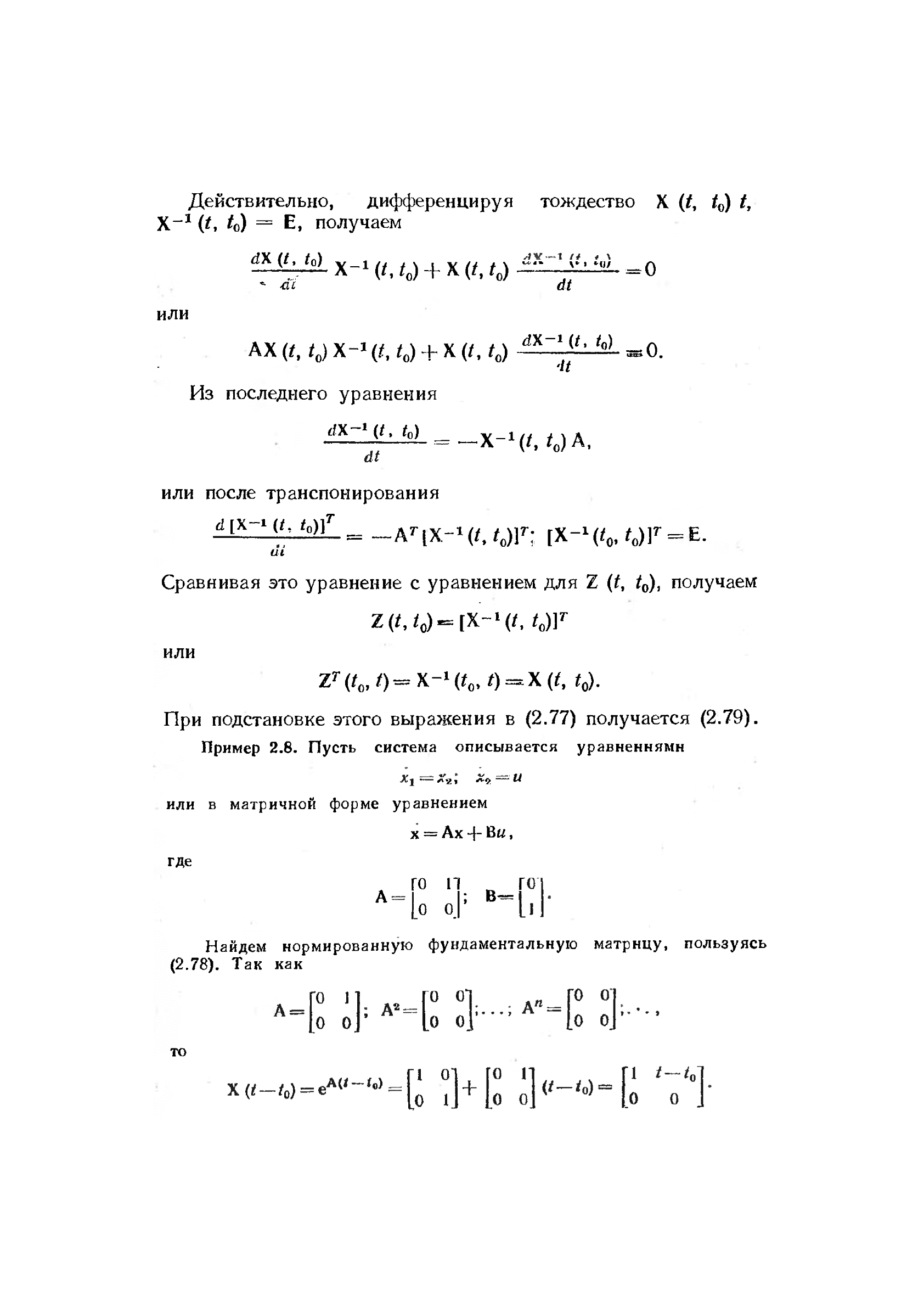
Действительно, дифференцируя тождество X (t, t

) t,

(t, to) = E, получаем

^HLJsL x-i (/, g + x (/, g —о

* ш dt

или

AX (/, g x-

(t, g + x (/, g

dX 1(t

• ^ »o.

'it

Из последнего уравнения

<*х-Ч'. У

= —х

(/, дд,

или после транспонирования

а[х-м< <„)]

-i

(/f

gjr.

,gF = E.

Сравнивая это уравнение с уравнением для Z (t, g, получаем

Z(U

)-[X~

(/, gr

или

z^g о-х-ч^О-х^, g.

При подстановке этого выражения в (2.77) получается (2.79).

Пример 2.8. Пусть система описывается уравнениями

— у ~

или в матричной форме уравнением

х =

Ах

+ В«,

где

ГО 11 Г

; В—

О 0.

Найдем нормированную фундаментальную матрицу, пользуясь

(2.78). Так как

то

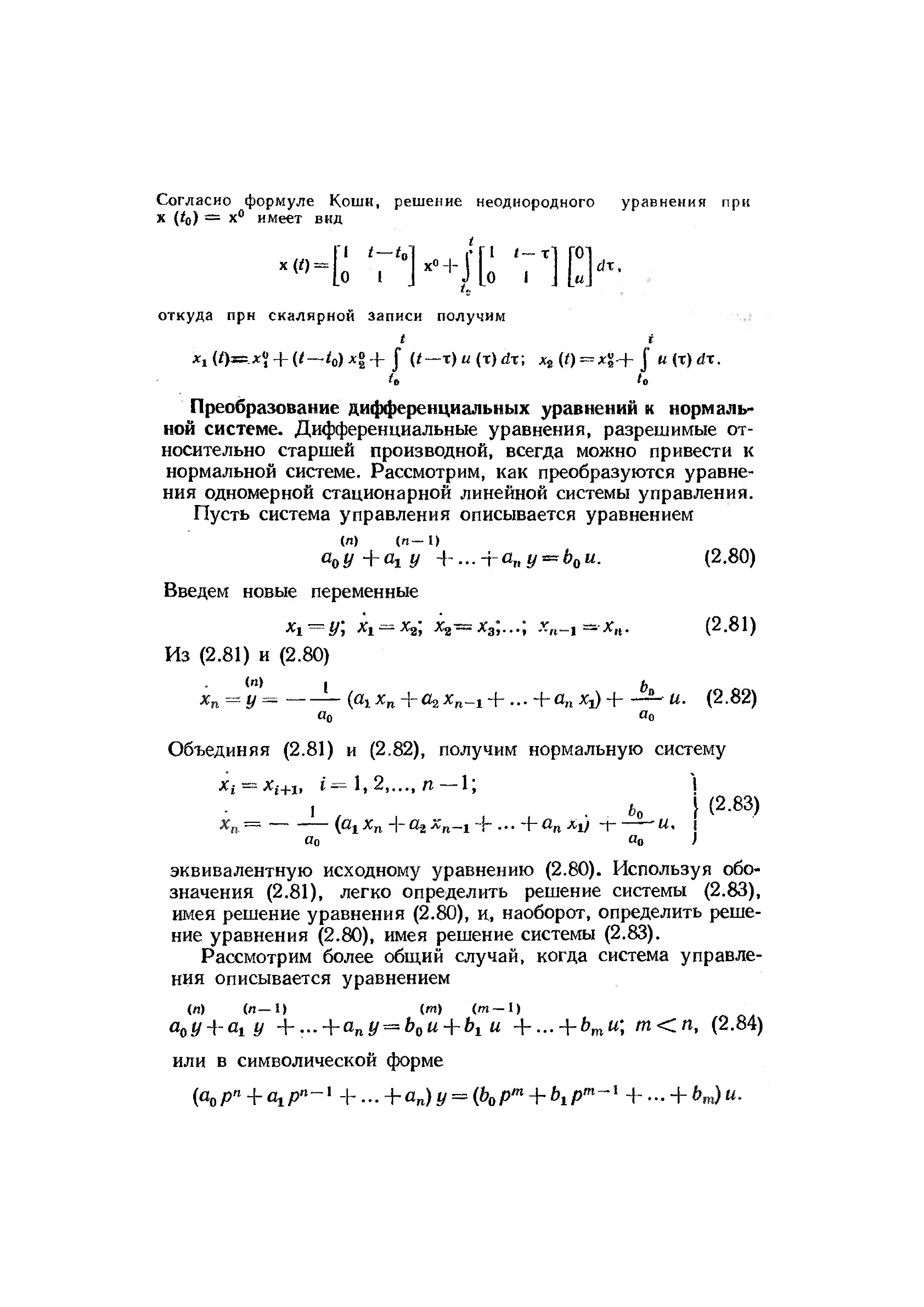
Согласно формуле Коши, решение неоднородного уравнения при

х (t

) = х° имеет вид

-«-К 'П-/С

'71 [!]-

откуда прн скалярной записи получим

t t

(t)^.x\ +

(t—1

) X*

-f J (t

—т) и (T) dx\

(0 + J « (t) rft.

/о

Преобразование дифференциальных уравнений к нормаль*

ной системе. Дифференциальные уравнения, разрешимые от-

носительно старшей производной, всегда можно привести к

нормальной системе. Рассмотрим, как преобразуются уравне-

ния одномерной стационарной линейной системы управления.

Пусть система управления описывается уравнением

(п) (п~ I)

оУ+

гУ +...+<*пУ**Ь

и. (2.80)

Введем новые переменные

• • _

~у\

Х\ — х

y.,.

•— j

—

. (2.81)

Из (2.81) и (2.80)

(п) J £

—

— (<h

+ ... + а

) ч —

и.

(2.82)

Объединяя (2.81) и (2.82), получим нормальную систему

X/ =

Xi+i,

i -- 1, 2,..., n 1; I

I bo (

)

— (a

+ a

-f ... +

a„

и,

Oo «0 J

эквивалентную исходному уравнению (2.80). Используя обо-

значения (2.81), легко определить решение системы (2.83),

имея решение уравнения (2.80), и., наоборот, определить реше-

ние уравнения (2.80), имея решение системы (2.83).

Рассмотрим более общий случай, когда система управле-

ния описывается уравнением

(л) (л—1) (т) (m-i)

<*оУ

1У +.~+a

y^b

u + b

и +...+Ь

и; т<«, (2.84)

или в символической форме

(OoP

+ <hpn-* +...+а

)у = (Ь

р>

+ Ь

Учитывая, что в этом уравнении дифференциальные операто-

ры при выходной и входной величинах и обратные им опера-

торы коммутативны, запишем его в виде [3]

(а

+ а

р*~

+ ... +а

и =

или

У -

Фо

р'

+. +

)

\ (2.85)

и = (а

+ щ р

4-... +

я„)

. (2.86)

Введем обозначения

х2, х

^^ Хд,..х

~(2.87)

Учитывая их, из уравнения (2.86) получаем

I 1

= (х

Hh • ••

4~ Xj) и.

(*о ао

Объединяя это уравнение с уравнениями (2.87), получаем нор-

мальную систему

= I i^

2,,.., tt

-— 1 у

-sss

(^i +

~i~\r

• • •

4* 4-

—

cio

эквивалентную исходному уравнению (2.84). Выходная пере-

менная системы управления и новые переменные связаны со-

отношением [см. (2.85)]

т+1

4- Ь

+... + b

Xf,

Рассмотрим, наконец, как преобразуется к нормальной си-

стеме общее уравнение одномерной стационарной линейной

системы управления с двумя внешними воздействиями, кото-

рое запишем в виде

(п) (n—1) (п) <n—1)

У + а±У +... = +

+... + b

u +

(п) (п-1)

•

+ c

f + c

f +... + c

f. (2.88)

Здесь для удобства коэффициенты в правой части пронумеро-

ваны в обратном порядке. Кроме того, в уравнение (2.88) вклю-

чены производные входные величин и и / до п-го порядка вклю-

чительно. Но такая запись не нарушает общности, так как

если в действительности порядки старших производных вход-

ных величин меньше п и равны т и I соответственно, то это

значит, что в уравнении (2.88) коэффициенты Ъ

= = ...

... = bm+i = 0 и с

= с

= 0. Уравнение (2.88)

может быть преобразовано в нормальную систему вида

= +

СС

и +

*а = *» +

(2.89)

п — 1

п +

"Г Pn-1 /»

— 2

n~k

и+1

+ Pn

где коэффициенты а* и р* определяют из следующих соотноше-

ний:

я-

]

* • » ?

п -

-1; а

= А— 2

n-k

к'у

k~0

tl — 1 — /

Ро К

-1 = 0,— S

~k~j

Pft>

k^O

,п

—i; P» —сь— 2

n~h P/f

(2.90)

Выходная величина у связана с фазовыми координатами ра-

венством

у = х

+ а

ы+Р(/. (2.91)

Доказательство эквивалентности уравнения (2.88) и системы

(2.89) при условии (2.90) и (2.91) имеется, например, в [8].

§ 2,9. Нестационарные линейные системы

Нестационарными линейными системами или линейными

системами с переменными параметрами называют системы, ко-

торые описываются линейными дифференциальными уравне-

ниями с переменными коэффициентами. Для их Описания по-

мимо дифференциальных уравнении могут быть использованы

передаточные функции, переходные и весовые (импульсные

переходные) функции, частотные функции и их характеристи-

ки. Кроме того, для графического представления нестационар-

ных систем могут быть использованы структурные схемы и гра-

фы. Однако методы, основанные на графических представле-

ниях, не так эффективны, как в случае стационарных систем.

Правила преобразования структурных схем и графов, уста-

новленные при изучении стационарных систем, в случае не-

стационарных систем несправедливы.

Рассмотрим некоторые способы описания одномерных не-

стационарных систем. Они могут быть обобщены на многомер-

ные системы так, как это было сделано при описании стационар-

ных линейных систем.

Так как для линейных систем (как стационарных, так и не-

стационарных) справедлив принцип суперпозиции, то'для про-

стоты можем ограничиться рассмотрением систем с одним вхо-

дом.

Уравнение одномерной нестационарной системы (объекта)

с одним входом в общем случае можно записать в виде

(п) (пг-1) (m) (т—1)

МОj+fliW j -К-i-MO0 = MO« + М9 и +...+

(t)

и (2.92)

или, в символической (операторной) форме

Q(P, f)y = R

iP>

t) и, (2.93)

где нестационарные линейные дифференциальные операторы

Q (л t) - а

рп

(t)p

[

+ ... + а

(t);

R(р, 0-ь

(0р™ + b

(t)p™~

+... {-b

(t).

Весовые функции. Как уже было определено, весовой функ-

цией называют решение уравнения (2.92) при и (f) — б (t — т)

и нулевых «начальных» условиях, т. е. функцию, которая опи-

сывает реакцию на единичный импульс системы, находящейся

в момент приложения импульса в исходном состоянии. Здесь

т обозначает момент приложения импульса и в определении

под начальными условиями понимают значения выходной ве-

личины

ее производных в момент т. При рассмотрении стаци-

онарных систем обычно в качестве начала отсчета времени при-

нимают момент приложения входного сигнала и поэто-

му в этих случаях полагают т = 0. В данном случае

этого де.лать нельзя. Реакция нестационарной системы зави-

сит не только от времени t — т, отсчитываемого от момента

приложения импульса, но и от самого значения т. Поэтому

весовая функция нестационарной системы — обозначим её

w {t — т, т) — являются функцией от двух переменных" от

текущего времени t и момента

приложения импульса.

Реакция — процесс на выходе системы — не может возник-

нуть до приложения входного сигнала: следствие не может

предшествовать причине. Поэтому

w (t—

т,

т) = 0 при t С т. (2.94)

Это условие называют условием физической осуществимости

или условием физической реализуемости. В случае стационар-

ной системы условие физической осуществимости имеет вид

w (t) = 0 при *< 0.

Получим формулы, определяющие связь между выходной

и входной величинами нестационарной линейной системы уп-

равления через ее весовую функцию. Так как, по определе-

нию, w (t — т, т) есть решение уравнения (2.93) при и

(£)

— 6 (t — т), то можем записать

Q (р, t) w (t - т, т) - R (р, t)b(t- т). (2.95)

Умножим обе части на и (т)

и проинтегрируем по т от —с»

до со, а затем, выиеся коэффициенты уравнения за знак инте-

грала (это возможно, так как они не зависят от т) и поменяв

местами операции интегрирования и дифференцирования, по-

лучим

оо оо

QOM) Г w(i

—т,

x)u(r)dx= R (р, t) J и

{х) Ь

(t—х) dx. (2.96)

— оо —

оо

Из определения дельта-функции

оо

J и (x)6(f—x)dx =u(t),

— оо

поэтому (2.96) можно переписать в виде

оо

Q(pJ) J w{t—T

X)u(r)dr ^R(p> t)u(t).

Из последнего равенства, которое выполняется тождественно,

вытекает, что функция

оо

y(t) = J W(t— Т, x)u(x)dx (2.97)

— оо

является решением уравнения (2.93) при произвольном задан-

ном и (t). Нижний предел интегрирования т = — оо в (2.97)

совпадает с моментом подачи входного воздействия. Поэтому

(2.97) является искомой формулой, определяющей связь меж-

ду выходной и входной величинами нестационарной линейной

системы в «установившемся» режиме. Учитывая условие фи-

зической осуществимости (2.94), формулу (2.97) можно запи-

сать также в виде

y(tj w(t —

x)u(x)dx. (2.98)

— оо

Аналогично, умножив обе части равенства (2.95) на и (т) dx

и проинтегрировав их от 0 до оо, получим формулу

со

Щ~~

—

)

(

)

определяющую выходную величину нестационарной линейной

системы, когда на ее вход подается воздействие и (t) в момент

t = О С учетом условия физической осуществимости ее также

можно записать в виде

у j w (t —т, т) и (т) dx.

Если зафиксировать переменную т, то весовая функция

w (t — т, т) будет функцией от одной переменной t, зависящей

от параметра т, и называться нормальной весовой функцией.

Нормальная весовая функция определяет изменение выходной

величины системы в течением времени при подаче на ее вход

единичного импульса в заданный момент т.

Если зафиксировать переменную t — рассматривать ее как

параметр^ — то весовая функция w (t — т, т) будет функцией

от одной переменной т и называться сопряженной

весовой

функ-

цией. Сопряженная функция определяет зависимость реак-

ции системы в фиксированный момент t от моменту т приложе-

ния единичного импульса.

Л>

Передаточные функции. Передаточная функция W (/?, t)

нестационарной системы в операторной форме определяется

также, как и передаточная функция стационарной системы

(в операторной форме) и равна отношению оператора R (/?, t)

воздействия к собственному оператору Q (р, *):

W(p

t)^R{p, t)/Q(p,t).

Понятие передаточной функции W (s, t) в изображениях

Лапласа требует уточнения. Его нельзя определять как отно-

шение изображений выходной и входной величин, так как при

этом не ясно, как вычислять W (s, t) по заданному дифферен-

циальному уравнению системы. Кстати, между передаточными

функциями W (р

0 и W (s, t) нет такой простой связи, как это

было между передаточными функциями W (р) и W (s) стацио-

нарных систем.

Перейдем к определению передаточной функции W (s, t).

Для этого воспользуемся физическим свойством частотных

передаточных функций.

Как известно, частотная передаточная функция

W(j<o)

ста-

ционарной системы имеет следующий физический смысл: ее

модуль равен отношению амплитуд гармонических колебаний

на выходе и входе системы, а ее аргумент—сдвигу фазы. Час-

тотная передаточная функция W (/со) стационарной системы

связана с ее передаточной функцией W

(s)

соотношением

Аналогичная связь должна существовать между частотной

передаточной функцией W (/со, t) нестационарной системы и ее

передаточной функцией W (s, tf). Поэтому, определив частот-

ную передаточную функцию W (/со, /), автоматически получим

определение передаточной функции W (s, t).

Как будет показано дальше, при подаче на вход нестацио-

нарной линейной системы гармонического сигнала на ее выхо-

де устанавливается «гармонический» сигнал той же частоты,

но с переменной амплитудой. И частотную передаточную функ-

цию W (/со, t) определим как такую, зависящую от параметра

t комплекснозначную функцию от частоты, у которой модуль

равен отношению амплитуд «гармонических» колебаний на вы-

ходе и входе нестационарной системы, а аргумент — сдвигу

фазы.