Воронов А.А. Теория автоматического управления. Часть первая

Подождите немного. Документ загружается.

вами, возмущенным движением системы называют всякое

иное движение системы, отличное от невозмущенного.

Введем новые переменные

Xi^ytW-ytV), (3.9)

равные разности переменных

у-

в возмущенном и невозмущен-

ном движении. Переменные х

называют отклонениями или

вариациями величин y

. Если все отклонения равны нулю

= 0; х

= 0; ...; = 0, (3.10)

то возмущенное движение y

(t) будет совпадать с невозмущен-

ным движением yl (/), т. е. невозмущенному движению отве-

чают нулевые значения переменных x

Пусть при t = to переменные x

принимают какие-либо на-

чальные значения x

, из которых по крайней мере одно не

равно нулю:

Xio ~ (3-Н)

Начальные значения отклонений (3.11) называют возмуще-

ниями.

А. М. Ляпуновым было дано следующее определение устой-

чивости: невозмущенное

движение

называют устойчивым по от-

ношению к переменным x

если при всяком произвольно задан-

ном положительном числе е, как бы мало оно ни было, можно

выбрать другое такое положительное число 6 (е), что при вся-

ких возмущениях x

, удовлетворяющих условию

2 (3.12)

и при любом t ^ t

будет выполняться неравенство

2 х? V) < е, (3.13)

i=? 1

в противном случае движение неустойчиво.

Определению устойчивости А. М. Ляпунова можио дать следующую

геометрическую интерпретацию. Совокупность отклонений х

, х

• •'»

в /г-мерном пространстве переменных x

, ...» х

определяет

точку М (ее называют изображающей точкой). В возмущенном движе-

нии при Изменении величин х

1у

, х

изображающая точка будет

описывать некоторую траекторию. Невозмущенному движению xi — 0

отвечает неподвижная точка — начало координат.

Рассматривая, например, случай, когда i = 3, построим в трех-

мерном пространстве координат xt две сферы: сферу е = 2 xf с ра-

диусом ~l/e и сферу 6—2 хщ с радиусом 1/б. Выберем радиус сфе-

ры е произвольно малым. Если невозмущенное движение устойчиво,

то для этой сферы должна найтись другая сфера 6, обладающая следую-

щим свойством; изображающая точка Ж, начав свое движение из лю-

бой точки М

, лежащей внутри или иа поверхности сферы 6, при своем

дальнейшем движении остается всегда внутри сферы е, никогда не до-

стигая ее поверхности (рис. 3.3).

Если же невозмущениое движение неустойчиво, то траектория изо-

бражающей точки М с течением времени пересечет сферу е изнутри на-

ружу (или попадет на ее поверхность) при сколь угодно близком поло-

жении точки М

к началу координат.

Заметим, что при i > 3 надо рассматривать движение изображаю-

щей точки в многомерном пространстве относительно гиперповерхно-

стей (гиперсфер) и рассмотрение теряет наглядность.

Практически устойчивость данного невозмущенного дви-

жения означает, что при достаточно малых начальных возму-

щениях возмущенное движение будет сколь угодно мало от-

личаться от невозмущенного движения. Если невозмущенное

движение неустойчиво, то возмущенное движение будет отхо-

дить от него, как бы малы ни были начальные возмущения.

Если невозмущенное движение устойчиво и при этом любое

возмущенное движение при достаточно малых начальных воз-

мущениях стремится к невозмущенному движению, т. е.

lim х

(t) = 0, (3.14)

t—>оо

то невозмущенное движение называют асимптотически устой-

чивым.

При асимптотической устойчивости изображающая точка

с течением времени должна неограниченно стремиться к нача-

лу координат, не выходя из сферы е.

Отметим некоторые особенности определения устойчивости

по А. М. Ляпунову. Во-первых, предполагают, что возмуще-

ния налагаются только на начальные условия, иначе говоря,

возмущенное движение происходит

при тех же силах (источниках энер-

гии), что и невозмущенное движение.

Во-вторых, устойчивость рассматрива-

ют на бесконечно большом промежут-

м, 1М

* X 1 1 ке времени. В-третьих, возмущения

предполагаются малыми. Несмотря на

/ эти ограничения, определение А. М.

Ляпунова устойчивости движения

является эффективным и плодотвор-

Рис. з.з ным в приложениях.

^ 1

' **

,§ 3.3. Теорема А. М. «Ляпунова об устойчивости

движения по первому приближению

Когда известно общее решение дифференциальных уравне-

ний движения (3.1), можно непосредственно определить зна-

чения переменных y

(t) в возмущенном движении, составить

вариации x

(/) — y*(t) и, исследуя их, решить вопрос об

устойчивости невозмущенного движения у\ (/). Однако, как

правило, исследование устойчивости

•

движения производят

не путем анализа общего решения, а методами, основанными

на качественном анализе дифференциальных уравнений воз-

мущенного движения, которым удовлетворяют отклонения

(вариации) x

Чтобы вывести уравнения возмущенного движения, найдем

из (3.9) переменные y

(t) = у\ (f) -f x^t) и подставим эти

значения y

(*) в дифференциальные уравнения движения (3.1).

Тогда

dynt)/dt'hdXi(tV<lt = YiW+Xi,

УЪ

+ х

у*

+ х

, О- (

ЗЛ5

Если правые части уравнений (3.15) допускают разложение в

степенные ряды Тейлора, то после этого разложения по степе-

ням x

получим

dy? (t) dxi (t)

dt dt

==*7r- = Yt{y

u У2, Уп, O + МгЧ * +

\ dx

(

*n+Ri(x1, ..., X

)

(3.16)

где Rt (x

, x

) совокупность членов, зависящих от

отклонений x

в степени выше первой.

Учитывая (3.4), будем иметь

(t)ldt^a

+ a

xb + ... + cL

+ R

, х

). (3.17)

В уравнениях (3.17) коэффициенты

№) (3.18)

в общем случае являются функциями времени t\ в частности,

они могут быть постоянными. В дальнейшем, если не будет

оговорено особо, будем считать коэффициенты a

постоянными.

Уравнения (3.17) называют дифференциальными уравне-

ниями возмуиленного движения.

Если отклонения x

достаточно малы, то, пренебрегая

Ri(x

лг

, ..., х

)

получим линеаризованные уравнения

/dt=-a

+ a

+...+a

i = l, 2, ..., n, (3.19)

называемые уравнениями первого приближения.

Во многих случаях устойчивость движения исследуют по

уравнениям первого приближения. Это объясняется не только

простотой этого метода, но также и тем, что знания процессов,

происходящих в реальных системах, позволяют надежно оп-

ределять только первые линейные члены. Однако на основа-

нии уравнений первого приближения можно дать иногда не-

верное заключение об устойчивости движения. Поэтому, ес-

тественно, возникает вопрос об определении условий, при вы-

полнении которых по уравнениям первого приближения можно

дать правильные ответы об устойчивости движения. Эту ис-

ключительно важную и принципиальную для теории автомати-

ческого управления задачу впервые поставил и решил

А. М. Ляпунов.

Системе уравнений (3.19) соответствует характеристичес-

кое уравнение, которое можно записать следующим образом:

D(s) =

Я-11

&12

^21 ^22 & •••

^пЪ ••• Я

пп

-0. (3.20)

Из (3.20) можно найти его корни s

, где i — 1, 2, п, ко-

торые в общем случае имеют вид s

= a

± /co

гдеа

- и —

вещественные и мнимые части корней соответственно.

Для исследования устойчивости систем по их линеаризо-

ванным уравнениям принципиально важны следующие тео-

ремы А. М. Ляпунова, которые приведем без доказательства.

Теорема 1. Если вещественные части всех корней s

харак-

теристического уравнения (3.20) первого приближения отри-

цательны, то невозмущенное движение асимптотически устой-

чиво.

Теорема 2. Если среди корней s

характеристического урав-

нения (3.20) первого приближения имеется хотя бы один ко-

рень с положительной вещественной частью, то невозмущен-

ное движение неустойчиво.

Если среди корней характеристического уравнения имеет-

ся один или несколько нулевых корней, а вещественные час-

ти остальных корней отрицательны, то этот случай называют

критическим. Дак показал Ляпунов, в критическом случае

устойчивость (неустойчивость) невозмущенного движения не

может быть оценена по уравнениям первого приближения, так

как она зависит от вида нелинейной функции R

), и поэтому в этом случае требуется рассмотрение дифферен-

циальных уравнений возмущенного движения (3.17) в их ис-

ходном виде.

Теоремы Ляпунова имеют весьма важное значение, так как

они позволяют судить об устойчивости нелинейных систем по

их линеаризованным уравнениям (уравнениям первого при-

ближения).

§ 3.4. Условия устойчивости линейных систем

автоматического управления

Покажем, как на основе изложенного выше определения

устойчивости А. М. Ляпунова можно найти условия устойчиво-

сти линейных (линеаризованных) систем автоматического уп-

равления.

Дифференциальное уравнение линейной системы автома-

тического управления, записанное для регулируемой выход-

ной величины х (t) при наличии управляющего воздействия

g (t), имеет вид

(аоР

+ а

+ ...+а

) х

(*)

-ФоР

+ Ь

+.~+b

)g(t), (3.21)

где я

, а

и b

...

— постоянные коэффициенты,

а р — d/dt — оператор дифференцирования.

Изменение регулируемой величины х (t) при произвольном

внешнем воздействии g (t) представляет собой решение урав-

нения (3.21):

X (t) = х

(0 + х

св

(t). (3.22)

В (3.22) первое слагаемое х

(0 — вынужденная составляю-

щая, имеющая тот же характер, что и правая часть уравнения

(3.21). Она определяется как частное решение неоднородного

дифференциального уравнения (3.21) с правой частью:

(а

+ а

+ + а

) х

(t) =

- ФоР

+ К Р

+ + Ь

) g

(t).

(3.23)

Второе слагаемое х

сВ

(t) —

свободная

(переходная) составляю-

щая, которая определяется общим решением однородного диф-

ференциального уравнения (3.21) без правой части:

(а

р" + а

рп-1 + ... + а

) х

св

(/) -0. (3.24)

Обычно в теории автоматического управления интересуют-

ся устойчивостью вынужденной составляющей х

(t) переход-

ного процесса. Поэтому за невозмущенное движение системы

необходимо принять вынужденную составляющую переходно-

го процесса х

(t). Тогда возмущенным движением будет любое

возможное в системе изменение регулируемой величины х (t),

а отклонением или вариацией — свободная составляющая j

*св (t) = х (/) —X

(t).

Возмущениями, по А. М. Ляпунову, являются начальные

значения л:

св

, которые возникли в моменх^^^под действи-

ем внезапно подействовавших дополнительных внешних сил,

т. е. начальные значения х

св0

. Дифференциальными уравне-

ниями возмущенного движения первого приближения в дан-

ном случае будут уравнения (3.24).

| В соответствии с определением устойчивости по А. М. Ляпу-

нову система будет асилттотически устойчивой, если с тече-

нием времени при t

->•

оо

свободная составляющая

будет стре-

миться к нулю, m. е. х

св

(t) 0. Чтобы найти эту составляю-

щую, необходимо решить дифференциальное уравнение (3.24):

= (3.25)

Решение уравнения (3.25) находят как х

св

(t) = Ce

Дифференцируя это выражение п раз и подставляя в (3.25),

после сокращения на общий множитель Ce

получаем

+ ...+а

=0. (3.26)

Полученное алгебраическое уравнение (3.26) называют

характеристическим уравнением. Его корни s

, s

будут определять характер переходного процесса в системе.

Нетрудно заметить, что по своему виду левая часть уравнения

(3.26) совпадает с дифференциальным оператором при выход-

ной величине в уравнении (3.21), поэтому характеристичес-

кое уравнение получают обычно, приравнивая к нулю диф-

ференциальный оператор при выходной величине в исходном

дифференциальном уравнении (3.21), т. е.

р»

+ а

+... +

«п

= 0. (3.27)

Следует заметить, одна-

ко, что в характеристичес-

ком уравнении (3.27),

р = s означает уже не сим-

вол дифференцирования,

а некоторое комплексное

число.

Решение характеристи-

ческого уравнения степени

п содержит п корней. Кор-

ни характеристического

уравнения обыкновенного

линейного дифференциаль-

ного уравнения с постоян-

ными коэффициентами могут быть вещественными, комплекс-

ными попарно сопряженными, мнимыми попарно сопряжен-

ными, нулевыми. В общем случае

Si = «£ + /*>*. (3.28)

На рис. 3.4 показаны возможные положения корней в ком-

плексной плоскости корней s при

= a

* s

= а

+ Л»s

= а

— /со

; s

= 0; s

= — «5; % = —

e + /««; = — «в — /<°б-

Если все корни разные, то их называют простыми. Если

среди корней есть одинаковые, то их называют кратными.

Обычно корни с отрицательными вещественными частями

принято называть левыми, поскольку они в комплексной пло-

скости корней расположены слева от мнимой оси, а корни с

положительными вещественными частями — правыми корнями.

Условие устойчивости линейной системы формулируется

следущим образом: для того чтобы линейная система была

асимптотически устойчива, необходимо и достаточно,

чтобы все

корни ее характеристического уравнения (3.27) были

левымио

Указанное условие устойчивости легко пояснить, рассматривая

решение однородного уравнения (3.25), которое при отсутствии крат-

ных корней имеет вид

*св(0= S

' (

1=1

где si — корни характеристического уравнения (3.27); С* — постоян-

ные интегрирования, определяемые из начальных условий.

Заметим, что корни характеристического уравнения зависят

только от вида левой части дифференциального уравнения (3.21) ли-

нейной системы. Постоянные интегрирования Ci зависят и от вида

правой ее части, поэтому быстота затухания и форма переходного про-

цесса определяются как левой, так и правой частями исходного диф-

ференциального уравнения (3.21). Однако, поскольку в понятие устой-

чивости входит только факт наличия или отсутствия затухания переход-

ного процесса, устойчивость линейной системы не зависит от вида пра-

вой части дифференциального уравнения (3.21) и определяется только

характеристическим уравнением (3.27).

При составлении (3.21) предполагалось, что внешние возмущаю-

щие воздействия отсутствуют. Если записать дифференциальные урав-

нения движения системы относительно возмущающего воздействия, то

в этом случае левая часть (3.21) остается без изменения, а правая будет

иметь другой вид. Так как характер переходного процесса в линейной

системе определяют только по виду левой части дифференциального

уравнения (3.21), то для определения качественной картины переход-

ных процессов лрактйчески безразлично, записать ли исходное диффе-

ренциальное уравнение для управляющего или возмущающего воздей-

ствия.

Вещественным корням характеристического уравнения S£ = щ

в (3.29) соответствуют слагаемые, представляющие собой экспоненты

СС-t

е '

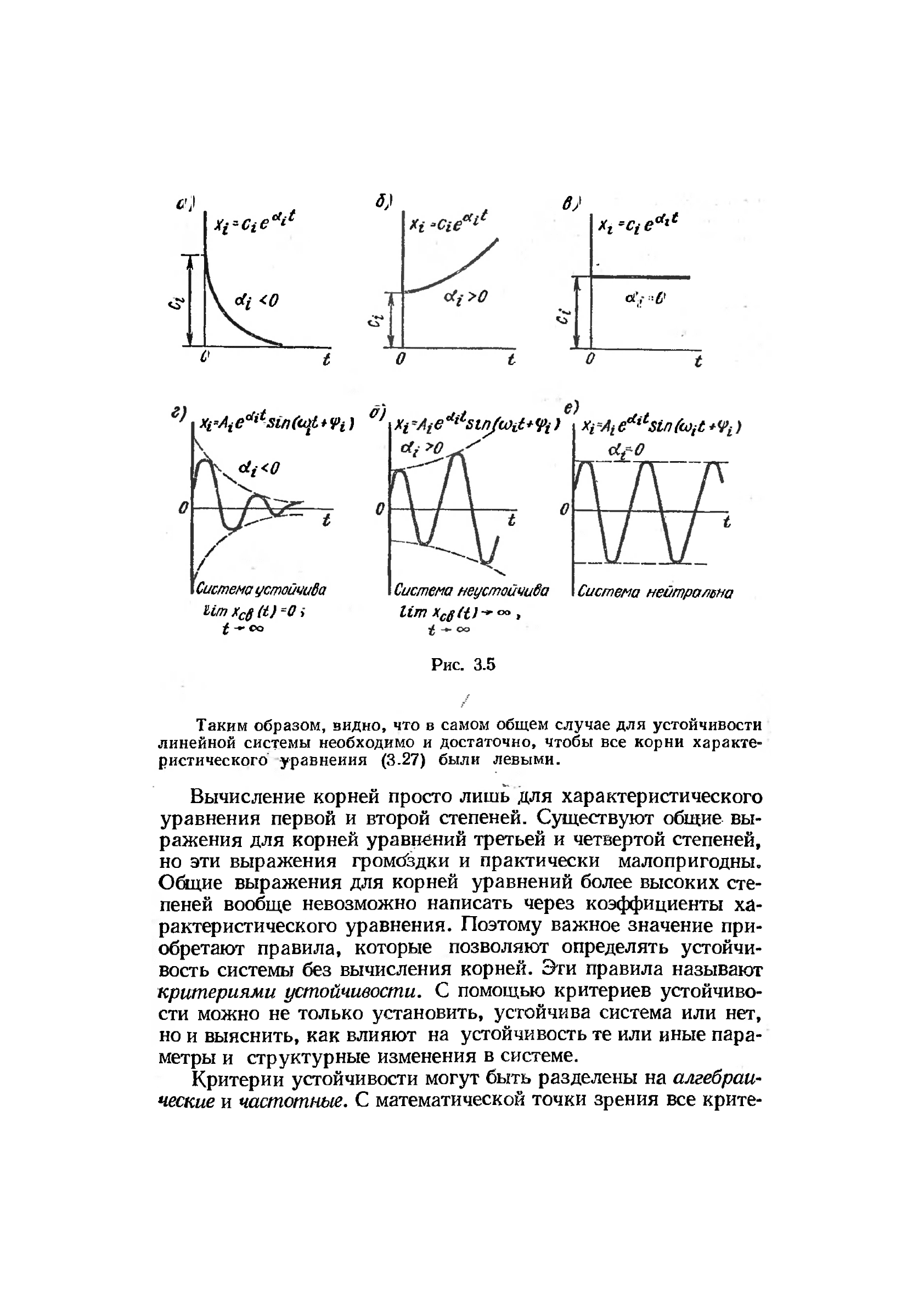
Очевидно, что отрицательным (левым) корням а* < 0 соответст-

вз'ют затухающие экспоненты (рис. 3.5, а), положительным (правым)

корням <%i > 0 — возрастающие экспоненты (рис. 3.5, б) и при нуле-

вых корнях щ = 0 слагаемые представляют собой прямые, параллель-

ные оси времени (рис. 3.5, е). ^

Комплексные кории характеристического уравнения всегда бы-

вают попарно сопряженными: S£ = щ + /<й£ и Sf

— К/ — /о>£.

Слагаемые, определяемые этими корнями в (3.29), могут быть при

использовании известной формулы Эйлера е

= cos со^ «±

...

(а-Ь/оь)* ,

<а

—/со-)*

sin представлены в виде Qe

1 1

+ Cj

1 1

—

ос

= Ле * sin (соj t + 'Фг)» где A

и — новые постоянные.

В этом случае при щ < О получаются затухающие колебания

(рис. 3.5, г), при ctj > 0 — расходящие колебания (рис. 3.5, д) и при

<Х£ = 0 — незатухающие колебания (рис. 3.5, е). Для устойчивости

и в этом случае необходимо выполнение условия а£ < 0. В самом об-

щем случае среди корней характеристического уравнения (3.27) могут

быть кратные корни. Если имеется г кратных корней то в (3.29)

появятся слагаемые вида

(С|,

г—1

+ ...+Ct 1 t+Ciо) eV.

• \

Если корень — оь* ± /со* имеет отрицательную вещественную

-t

часть щ < 0, то множитель е

будет с течением времени убывать.

Множитель в скобках неограниченно растет, поэтому мы имеем неопре-

— los-lf ^

деленность оо*0. Однако известно, что е

быстрее стремится к

нулю, чем выражение /

, поэтому при «£ < 0 эта группа слагае-

мых с течением времени также стремится к нулю.

а)

Xi-de'it

оli

в)

otf'O

xr^e^si/jCajl^i)

Xie

dii

sinju)it*<Pf) xie

dit

sinfcojt

di<0

Система устойчива

Um х

£ — Co

Система

неустойчива

g(t)

Система нейтральна

Рис. 3.5

Таким образом, видно, что в самом общем случае для устойчивости

линейной системы необходимо и достаточно, чтобы все корни характе-

ристического уравнения (3.27) были левыми.

Вычисление корней просто лишь для характеристического

уравнения первой и второй степеней. Существуют общие вы-

ражения для корней уравнений третьей и четвертой степеней,

но эти выражения громоздки и практически малопригодны»

Общие выражения для корней уравнений более высоких сте-

пеней вообще невозможно написать через коэффициенты ха-

рактеристического уравнения. Поэтому важное значение при-

обретают правила, которые позволяют определять устойчи-

вость системы без вычисления корней. Эти правила называют

критериями устойчивости. С помощью критериев устойчиво-

сти можно не только установить, устойчива система или нет,

но и выяснить, как влияют на устойчивость те или иные пара-

метры и структурные изменения в системе.

Критерии устойчивости могут быть разделены на алгебраи-

ческие и частотные. С математической точки зрения все крите-

рии устойчивости эквивалентны, однако целесообразный вы-

'бор того или иного критерия устойчивости при решении кон-

кретных задач позволяет провести исследование устойчивости

наиболее простым путем.

§ 3.5. Алгебраические критерии устойчивости

Алгебраические критерии устойчивости позволяют судить

об устойчивости системы по коэффициентам характеристичес-

кого уравнения

D(s) ^a

-\-а

...

+а

— 0.

(3.30)

Из алгебраических критериев устойчивости наиболее ши-

рокое распространение получили критерии устойчивости Ра-

уса и Гурвица.

Прежде чем познакомиться с ними, заметим, что необходи-

мым условием устойчивости системы любого порядка является

положительность всех коэффициентов характеристического

уравнения (3.30):

>0; а

> 0; ...; а

> 0. (3.31)

Действительно, в соответствии с теоремой Безу уравнение

$.30) можно представить в виде произведения множителей,

содержащих корни s

.... s

(s — s

)(s — s

)...(s — s

) = 0. (3.32)

Если все корни характеристического уравнения будут от-

рицательны, то все множители выражения (3.32) будут иметь

вид

(s +. |aj)(s + |a

|)... (s + |a„|) = 0. (3.33)

где St = — \a,i

— значения корней.

Производя перемножение в (3.33), получим (3.30), в кото-

ром все коэффициенты будут определяться положительными

членами [а*| выражения (3.33), т. е. будут положительны.

/Если характеристическое уравнение (3.30) имеет комплекс-

ное корни с отрицательными вещественными частями, то оно

может быть представлено в виде

(s + KI) (S +

|а

— "/«г) (s I К! + (s +

+ Ы = о