Воронов А.А. Теория автоматического управления. Часть первая

Подождите немного. Документ загружается.

или

(Т

р+ 1К + Р<Р = (2.126}

'я

где Г

= LJr'

— электрическая постоянная времени цепи

якоря.

На основе законов механики можно записать уравнение

для моментов

j£± — м

2 вр с

или

<р =•

вр

— М

, (2 А 27}

где J — момент инерции вала двигателя (с учетом нагрузки);

Л1

вр

— вращающий момент; М

— момент сопротивления.

Вращающий момент пропорционален току якоря:

(2.128)

Значение постоянной с

, как и с

, зависит от тока возбужде-

ния и конструкции двигателя.

Исключив из (2.126), (2.127) и (2.128) момент М

вР

ток /я, получим

(Т

р +1) (р

+ — м

)+-Ё-

- 4-1.

V с

j я

Это уравнение можно преобразовать к виду

(Т

вм

+ Т

р 4-

1) РФ

= w

—А

(Т

пР

+1)М„ (2.129)

т„ = Jr'Jc

— электромеханическая постоянная вре-

мени; kfr — с

и &

д2

= Гя/с

— передаточные коэффициен-

ты.

В изображениях Лапласа уравнение двигателя принимает

вид:

(Тя Пм

+ 4- 1) 5Ф

(S)

= - (Г

5 + 1) M

(s),

(2.130)

где £/

(s) -L {u

}; М

(s) = L {М}

Передаточные функции двигателя имеют вид:

по управляющему воздействию

' (Т

вм

р* + Тъ

р+1)р

(S) =

(Т

&ы

S+

s '

по возмущению (моменту сопротивления М

)

(р)

^яР+В ;

Тем Р

~\~Там

Р+

1) Р

(s) —

- g ^

2(7

s+I)

(Л,

I )

Структурная схема приведена на рис. 2.31, в, откуда видно,

что математическая модель двигателя может быть представ-

лена: по возмущению — в виде последовательного соедине-

ния форсирующего, колебательного (или двух апериодиче-

ских, если Г

0М

С 2УТ

9М

) и интегрирующего звеньев, а по

управляющему воздействию — колебательного (или двух апе-

риодических, если Т

зм

< 2"|/

) и интегрирующего звень-

ев.

Усилитель, сравнивающее звено, делитель напряжения.

Эти элементы -описываются уравнениями

= k

e\ —ц

;

—

(2.131)

где k

— коэффициент усиления усилителя; k

— «коэффи-

циент деления» делителя.

Линеаризованное уравнение генератора связывает отклоне-

ние Ди

с внешними воздействиями ф и/, Поэтому небходи-

мо преобразовать систему уравнений (2.131), так, чтобы она

зависела от отклонения Ди

(а не от и

Запишем последние два уравнения системы (2.131) следу-

щим образом:

е=

Ион

+ Д^о— (^д.н +

"д);

л-н + А^д =

("г-н

+ (2.132)

где и

0нУ

«д.

— номинальные значения задающего воздействия

и напряжения делителя, определяемые равенствами

«д.н = К «он = "

.н- (2.133)

Уравнения (2.132) с учетом (2.133) можно записать так:

Д «

= й

Д«

; е ~ Д«

—

В изображениях Лапласа уравнения усилителя, сравниваю-

щего устройства и делителя напряжения принимают следую-

щий вид:

(s) = k

E(s); E(s)=U

(s)-U

(sy

(s)

где E(s)=L {e}; U

(s) ==

L 1/

(s)

= L {Д«

Рис. 2.32

Передаточные функции усилителя W

и делителя W

имеют

вид

Эти звенья являются пропорциональными. Сравнивающее

звено имеет два входа и описывается двумя передаточными

функциями: передаточной функцией по входу, куда подает-

ся уменьшаемое,

(p) - W

(s) = 1,

и передаточной функцией по входу, куда подается вычитае-

мое,

(р) «

(s) = I.

Уравнение и передаточные функции системы. На рис. 2.32

приведена структурная схема САР напряжения генератора, со-

ставленная по полученным уравнениям и передаточным функ-

циям отдельных элементов. Используя правило нахождения

передаточной функции одноконтурных систем, определим ее

передаточные функции.

Передаточная функция разомкнутой системы

W - ,

(т

где k = к

д1

г1

— передаточный коэффициент разомкну-

той системы.

Передаточные функции прямой цепи:

по задающему воздействию Au

= по моменту

сопротивления М

ОД/ _

&Д2 ^П

(Уя Т

ам

* + s+ 1) (Г

s+1) s '

по возмущению / W

= /г

Для передаточных функций замкнутой системы (относительно

выхода Аи

) имеем: по задающему воздействию Аи

- W

+ W) = — Ь

«о sr + a

+ G

+ A

s+ C

где k

^kjk

;

= T

; a

= (Т

-\- Г

) Г

эм

;

а2

= Г

эм

+ Г

; c

=l; =

по моменту сопротивления Л1

«^„М

= W

.J(\ + W)- '

u S+b

J —-,

щ s

sr+a

s-j- a

где fe

— Л

д2

\ Ь

= fe

; по возмущению f

+ c

+ «з s)

flo +

«1 S

«2 S

+«3

Уравнение системы в символической форме имеет вид

hu^W

-{-W

или

(а

+ s

+ а

-f а

s + а

) = k

—

— (b

s +

)

-f k

(а

+ а

+ s

-f a

s) f.

|Л

Об обозначениях передаточных функций. Выше использо-

вались два обозначения для передаточных функций: W (р)

и W (s). Первое указывает на то, что передаточная функция

рассматривается как некоторый оператор, осуществляющий

преобразования входной величины и (t) в выходную х (t). Это

записывается в виде соотношения

x = W(p)u. (2.134)

Для вычисления х по заданным и и W (р) требуется решать

дифференциальное уравнение, т. е. достаточно простой рас-

шифровки W (р), позволяющей перевести W (р) на язык алго-

ритмов, нет, и (2.1.34) следует рассматривать скорее как сим-

волическую запись дифференциального уравнения. Второе

обозначение W (s), полученное из изображений Лапласа X (s) и

U (s) для переменных х (t) и и (t), указывает на то, что W (s)

рассматривается как обычная функция комплексной перемен-

ной s. В этом случае можно записать

X(s) = W(s)U(s) (2.135)

с оговоркой, что это соотношение справедливо для нулевых на-

чальных условий. В этом случае W (s) используется, напри-

мер, для вычисления частотных характеристик W (/со).

Двойственность происхождения функций №(s) и W (р)

привела в литературе и к двойственности в обозначениях у

разных авторов. Мы в дальнейшем будем использовать, как

правило, обозначение W (s) для передаточных функций или

d (s) — 0 для характеристических уравнений, сохраняя обо-

значения W (р) для тех случаев, когда W(p) явно рассматри-

вается как оператор, а не как комплексная алгебраическая

функция, а также тогда, когда W (s) не совпадает с W (/?), на-

пример для систем с переменными параметрами. В последнем

случае часто в число аргументов функции W будет наряду с опе-

ратором р вводиться и параметр, от которого она зависит, нап-

ример W (р, t).

Глава 3

УСТОЙЧИВОСТЬ

ЛИНЕЙНЫХ СИСТЕМ

АВТОМАТИЧЕСКОГО

УПРАВЛЕНИЯ

§3.1. Понятие устойчивости

На любую автоматическую систему

всегда действуют различные внешние

возмущения, которые могут нарушить ее

нормальную работу. Правильно спро-

ектированная система должна устойчи-

во работать при всех внешних возму-

щениях.

В простейшем случае понятие устой-

чивости системы связано со способно-

стью ее возвращаться (с определенной

точностью) в состояние равновесия по-

сле исчезновения внешних сил, кото-

рые вывели ее из этого состояния. Если

система неустойчива, то она не возвра-

щается в состояние равновесия, из кото-

рого ее вывели, а либо удаляется от

него, либо совершает вокруг него недо-

пустимо большие колебания.

Наблюдения показывают, что некото-

рые положения равновесия системы ус-

тойчивы к небольшим возмущениям, а

другие принципиально возможные рав-

новесные положения практически не мо-

гут быть реализованы.

Наглядно устойчивость равновесия

представлена на рис. 3.1, где изображен

шар, расположенный в некотором уг-

лублении (рис. 3.1, а), на некоторой

выпуклой поверхности (рис. 3.1, б), на

плоскости (рис. 3.1, в).

Положение равновесия шара харак-

1еризуется точкой А

. В случае, изобра-

женном на рис. 3.1, а, при всяком откло-

нении шара от положения равновесия, например в точку А

1У

он будет стремиться снова возвратиться к положению равно-

весия — в точку Л о (при отсутствии сил трения) или к не-

которой конечной области, окружающей положение равно-

весия, например в точку Л

(при наличии сил трения). Та-

кое положение равновесия устойчиво. Случай, изображен-

ный на рис. 3.1, б, соответствует неустойчивому положению

равновесия. Рис. 3.1, в соответствует безразличному равно-

весию. На рис. 3.1, г состояние равновесия устойчиво лишь

до тех пор, пока отклонение не вышло за некоторую гра-

ницу, определяемую, например, точкой В. Выйдя за эту гра-

ницу, шар уже не вернется в точку Л

, а будет двигаться

вправо от точки В либо все время удаляясь, либо до нового со-

стояния равновесия в зависимости от формы поверхности, т. е.

в конечном счете в зависимости от уравнений движения шара.

Поэтому в общем случае, рассматривая нелинейные систе-

мы, вводят понятие устойчивости «в малом», «е большом» «в

целом». Система устойчива «в малом»,

если констатируют лишь факт нали-

чия области устойчивости, но не опре-

деляют каким-либо образом ее грани-

цы. Систему называют устойчйвой

«в большом», когда определены гра-

ницы области устойчивости, т. е. оп-

ределены границы области начальных

отклонений, при которых система

возвращается в исходное состояние,

и выяснено, что реальные начальные

отклонения принадлежат этой обла-

сти. В том случае, когда система воз-

вращается в исходное состояние при

любых начальных отклонениях, си-

стему называют устойчивой «в целом».

Устойчивость «в целом» для опреде-

ленного класса нелинейностей назы-

вают «абсолютной» устойчивостью.

Так, например, случай, изобра-

женный на рис. 3.1, а, соответствует

устойчивости «в целом», а случай,

изображенный на рис. 3.1, г, может

соответствовать. либо устойчивости

«в большом», либо устойчивости «в ма-

лой». Очевидно, что система, устойчи- р

ис

в)

шт шшя,

вая «в целом», будет устойчива «в большом» и «в малом»; систе-

ма, устойчивая «в большом», будет устойчива и «в малом».

На рис. 3.1, д изображено еще одно принципиально возмож-

ное для нелинейных систем состояние равновесия, которое на-

зывают полу устойчивым.

Для того чтобы дать определение устойчивости равновесия,

вводят понятие о невозмущенном состоянии равновесия, соот-

ветствующем состоянию покоя в точке А

на рис. 3.1, а, и

возмущенном состоянии, соответствующем, например, точке

1У

в которую внешняя сила привела шар и затем прекратила

свое действие. Система будет устойчивой, если из возмущенного

состояния она перейдет в некоторую заданную область, окру-

жающую невозмущенное состояние равновесия.

В рассмотренном выше примере с шаром вопрос об устой-

чивости решается довольно просто. Однако следует заметить,

что в общем случае далеко не всегда ясно, при каких усло-

виях равновесное положение системы будет устойчивым.

Понятие устойчивости можно распространить и на более об-

щий случай, когда в качестве невозмущенного состояния рас-

сматривают не положение равновесия системы, а ее движение,

например движения системы по некоторой наперед заданной

траектории.

Допустим, что заданное движение системы при отсутствии

возмущений должно определяться некоторым законом измене-

ния независимых координат у\ (г), у\

(£),

у*

(t). По анало-

гии со случаем равновесия положения, заданное движение

называют невозмущенным движением. Внешние возмущения,

действующие на систему, вызовут отклонение действительного

движения системы от заданного. Действительное движение си-

стемы называют возмущенным движением. Пусть действитель-

ное движение системы определяется независимыми координа-

тами у

(0, у2 (О*

Уп

(О- В общем случае у

(t) фу\ (t),

У2 (t) Ф Уг (0, Уп (t) Ф Уп (t).

Заданное^невозмущенное движение будет устойчивым, ее-

ли после приложения внешних сил (возмущений), которые за-

тем снимают, возмущенное движение по истечении некоторо-

го времени войдет в заданную область Iу\ (0 — yl (01 ^

где е

- =-const — заданные величины, i = 1,2,..., п.

Чтобы проиллюстрировать сказанное, предположим, что

невозмущенное движение происходит по траектории А, а воз-

мущенное движение происходит по траектории Б (рис. 3.2, а).

Возьмем на этих траекториях две произвольные точки N

, отвечающие одному и тому же моменту времени t. При

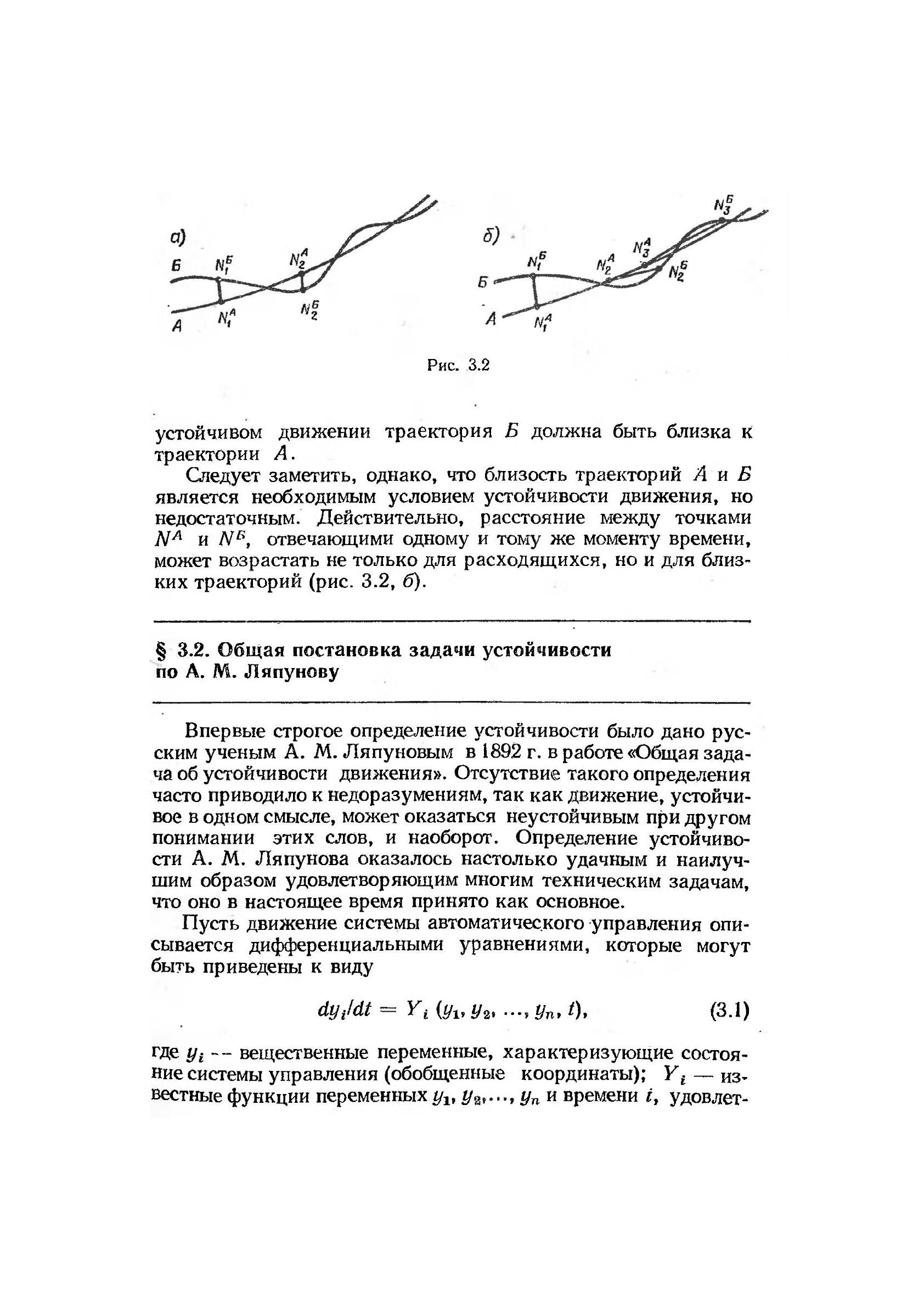
Рис. 3.2

устойчивом движении траектория Б должна быть близка к

траектории А.

Следует заметить, однако, что близость траекторий А и Б

является необходимым условием устойчивости движения, но

недостаточным. Действительно, расстояние между точками

и N

\ отвечающими одному и тому же моменту времени,

может возрастать не только для расходящихся, но и для близ-

ких траекторий (рис. 3.2, б).

§ 3.2. Общая постановка задачи устойчивости

по Д. М. Ляпунову

Впервые строгое определение устойчивости было дано рус-

ским ученым А. М. Ляпуновым в 1892 г. в работе «Общая зада-

ча об устойчивости движения». Отсутствие такого определения

часто приводило к недоразумениям, так как движение, устойчи-

вое в одном смысле, может оказаться неустойчивым при другом

понимании этих слов, и наоборот. Определение устойчиво-

сти А. М. Ляпунова оказалось настолько удачным и наилуч-

шим образом удовлетворяющим многим техническим задачам,

что оно в настоящее время принято как основное.

Пусть движение системы автоматического управления опи-

сывается дифференциальными уравнениями, которые могут

быть приведены к виду

dyjdt = Y

, t), (3.1)

где уi вещественные переменные, характеризующие состоя-

ние системы управления (обобщенные координаты); Y

— из-

вестные функции переменных у

уу

и времени удовлет-

воряющие условиям существования и единственности реше-

ния.

" Исходное состояние системы при t — t

однозначно опре-

деляется начальными значениями переменных у

которые

обозначим y

у2,01

^/no-

Каждой совокупности начальных значений у

,...,

соответствует единственное решение (3.1) для всех t > t

Уг ™ Уь(Ую» У•

••»

У.по* t). (3.2)

Решение (3.2) описывает какое-либо движение системы, оп-

ределяемое исходным состоянием.

Некоторое вполне определенное движение системы, подле-

жащее исследованию на устойчивость, называют невозмущен-

ным движением.

Заметим, что выбор невозмущенного движения является

произвольным. Это может быть любое возможное движение

системы, как установившееся, так и неустановившееся. До-

пустим, что в качестве невозмущенного движения выбрано та -

кое, которое описывается заданными функциями времени

Уг у\ (0; у г=Ж0;

Уп

у*

(0- (3.3)

Предположим, что функции (£) являются частным ре-

шением дифференциальных уравнений (3.1), т. е.

dyt (t)fdt - frf, yh */*, 0, (3.4)

удовлетворяющим начальным условиям при t ~ t

Ух =У\ {U)\ У2 =

У2(*оУ>

Уп —Уп (^о)- (3 5)

В частном случае, когда параметры системы не изменяют-

ся со временем и функции Y

не зависят явно от U движения

(3.3) являются установившимися. Им отвечают решения

у\ = const, (3.6)

служащие корнями уравнений

Уг {Уъ У2> Уп) = 0. (3.7)

Изменим условия (3.5), дав начальным значениям перемен-

ных у

*/п небольшие по модулю приращения е

, е

,...,

, т. е. пусть при t = t

Ух

У\

(Q +

Уг

ih) + е

; •• ;

Уп

= ^ (*

) f «п- (3.8)

Движение системы, отвечающее измененным начальным усло-

виям '(3.8), называют возмущенным движением. Другими ело-