Воронов А.А. Теория автоматического управления. Часть первая
Подождите немного. Документ загружается.


или
a
0
(s + \a
1
\)l(s + \a
2
\f +
(o
2
2
]
...
(s
+ )се
Л
|)=0. (3.34)
Уравнение (3.34) также приводится к виду уравнения
(3.30) с положительными коэффициентами.
Для систем первого и второго порядков
необходимое
условие
устойчивости является и достаточным условием устойчиво-
сти, поскольку в этом случае при положительных коэффи-
циентах характеристического уравнения все его корни явля-
ются левыми. Однако для систем третьего и высших порядков
положительность коэффициентов характеристического урав-
нения является необходимым условием устойчивости, но не
достаточным. В этом случае все вещественные корни характе-
ристического уравнения (если они есть) левые, комплексные
же корни могут быть и правыми.
Критерии устойчивости Рауса и Гурвица позволяют по
коэффициентам характеристического уравнения (3.30) без вы-
числения его корней сделать вывод об устойчивости системы.
Критерий устойчивости Рауса* Этот критерий устойчиво-
сти был в 1877 г. предложен английским математиком Э. Рау-
сом в виде некоторого правила (алгоритма), которое наиболее
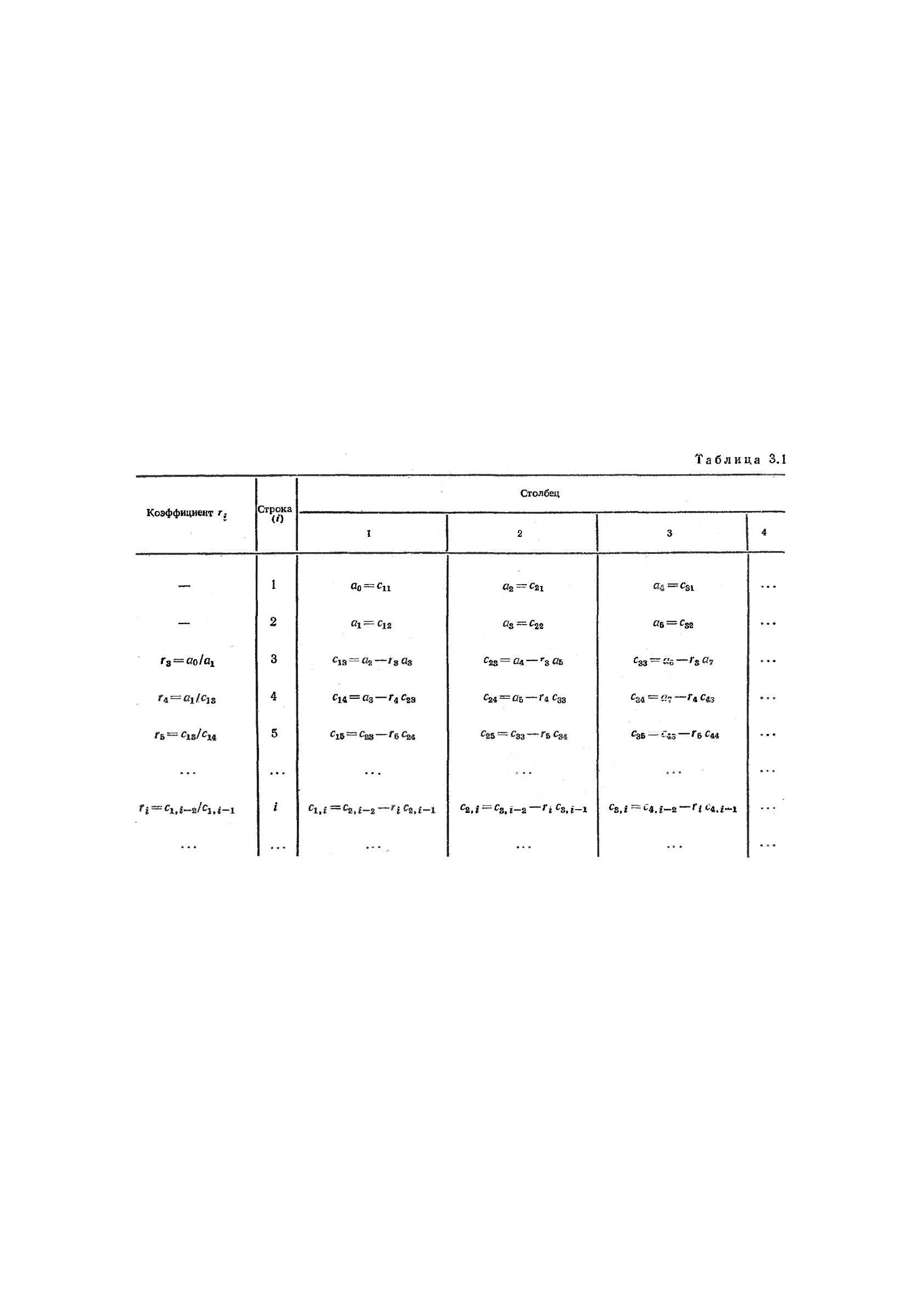
просто поясняется табл. 3.1.
В первой строке табл. 3.1 записывают в порядке возраста-
ния индексов коэффициенты характеристического уравнения
(3.30), имеющие четный индекс: а
0
, а
29
я
4
, a
e
, во второй
строке — коэффициенты (3.30) с нечетным индексом: a
l9
а
3
,
Любой из остальных коэффициентов таблицы определяют
как
Ch,
i
—
c
u+i, г-а —
r
i
Ck+1
T
z~U
(3.35)
где
г^а/Ci, j-i- (3.36)
В (3.35) и (3,36) k — индекс, означающий номер столбца
табл. 3.1; i— индекс, означающий номер строки табл. 3.1.
Заметим, что число строк таблиц Рауса равно степени ха*»
рактеристического уравнения плюс единица (п> + 1).
После того как таблица Рауса заполнена, по ней можно су-
дить об устойчивости системы. Условие
ч
устойчивости Рауса
формулируется так: для того
чтобы
система автоматического
управления была устойчива, необходимо и достаточно, чтобы
Таблица
3.1
Коэффициент r
f
Строка
(0
Столбец
Коэффициент r
f
Строка
(0
1 2
3
4
—
1
G
0
= C
U
а
2
— с
2
1
= C
Sl
...
—
2
% ~
С
22
^5 =
с
82
...
Г3
—ЯО/Gi
3
С
2&
=
&4 —
r
s аъ
С
33 ~
—
Г
S
о • «
4
г
14
=
с
3
—г
4
с
23
с
2
4 = аь —
f
4 ^зз С34 = —Г4 С^з
5
с
35 ' —Г
5 С44
...
« • •
i
...
c
2,i ~ ^s, г—2
—
г
г
с
з, г—1
c
s>
f
~
ё-г —
г г г-i

коэффициенты первого столбца таблицы Рауса имели один и
тот
же
знак, m. е. при а
0
>0 были положительными:
аз
^i,
п+1
> 0. (3.37)
Если не все коэффициенты первого столбца положительны,
то система неустойчива, а число правых корней характерис-
тического уравнения равно числу перемен знака в первом
столбце таблицы Рауса.
Критерий Рауса особенно удобен, когда заданы числовые
значения коэффициентов характеристического уравнения
(3.30). В этом случае определение устойчивости можно выпол-
нить довольно быстро даже при характеристических уравне-
ниях высокого порядка.
Форма алгоритма, с помощью которого составляют таблицу
Рауса, очень удобна для программирования ЭВМ, поэтому
критерий Рауса нашел широкое применение при исследова-
нии влияния на устойчивость либо коэффициентов характерис-
тического уравнения, либо отдельных параметров системы, не
очень сложным образом входящих в эти коэффициенты, с по-
мощью быстродействующих ЭВМ.
Пример 3.L Пусть характеристическое уравнение системы D (s)- =
=
S®
+ 6s
5
+ 21s
4
+ 44s
3
+ 62s
2
+ 52s + 100 = 0.
Для определения устойчивости системы по коэффициентам этого
уравнения составим таблицу Рауса (табл. 3.2).
Имеется две перемены знака коэффициентов первого столбца:
следовательно, система неустойчива, а характеристическое уравнение
имеет два правых корня.
Критерий устойчивости Гурвица. В 1895 г. немецким мате-
матиком А. Гурвицем был разработан алгебраический крите-
рий устойчивости в форме определителей, составляемых из
коэффициентов характеристического уравнения системы.
Из коэффициентов характеристического уравнения (3,30)
строят сначала главный определитель Гурвица
К =
Оу | а
г
а
0
а2
а,
а.
а
х
а
3
а
7
... и
а
6
... 0
а
ь
... 0
а
0
а% а^ ... ..
(3.38)
0 0 0 0 а

Таблица 3.2
Коэффициент г-
Строка
(0
Столбец <£)
Коэффициент г-
Строка
(0
1
2
3
4
•
а
0
=1
£72=21
с*
= 62
а
е
= 100
—
2
а
г
=6
сг
3
=44
а
5
= 52
а? = 0
=
1/6 —
0,167
3
с
13
=
21
—0,167-44= 13,65
с
23
= 62—0,167-52 =
с
33
= 100—0,167-0 =
0
•
= 53,3
= 100
a
\!
c
iz
~ 6/13,65
—
4
с
и
=
44
—
0,44 • 53,3
= 20,6
^24
=
52
—0,44-100 =
с
34
= 0-0,44-0=0
0
= 0,44 = 8
=
С
13/
С
14 =
5
с
15
= 53,3-0,66-8 = 48
с
25
= 100-0,66-0=
0
0
= 13,65/20,6 = 0,66
= 100
г
6
= с
1й
/с
г5
= 20,6/48 =
6
с
16
= 8—0,43-100= —35
с
2б
=
0
—0,43«
0
= 0
0
0
= 0,43
—
с
15
/с
16
= 48/
—35
=
7
с
17
=
100
—
( —
1,37).
0
=
0
0
0
= —1,37
= 100

по следующему правилу: по главной диагонали определите-
ля слева направо выписывают все коэффициенты характерис-
тического уравнения от a
L
до а
п
в порядке возрастания индек-
сов. Столбцы вверх от главной диагонали дополняют коэффи-
циентами характеристического уравнения с последовательно
возрастающими индексами, а столбцы вниз — коэффициента-
ми с последовательно убывающими индексами. На место коэф-
фициентов с индексами больше п (п — порядок характеристи-
ческого уравнения) и меньше нуля проставляют нули.
Отчеркивая в главном определителе Гурвица, как показано
пунктиром, диагональные миноры, получаем определители
Гурвица низшего порядка:
а
г
а
3
а
0
а
2
А* =
а
г
а
3
а
5
а
0
а
2
а
4
О a
t
а
3
A
k
=
а
х
а
3
а
ь
а
2
а^
О a
t
а
3
Як
(3.39)
Номер определителя Гурвица определяется номером коэф-
фициента по диагонали, для которого составляют данный опре-
делитель. Критерий устойчивости Гурвица формулируется
следующим образом: для того чтобы система
автоматическо-
го управления
была устойчива,
необходимо и
достаточно,
чтобы
все определители Гурвица имели знаки, одинаковые со зна-
ком первого коэффициента характеристического уравнения
а
0
, т. е. при а
0
Г> О
были положительными.
Таким, образом» при а
0
>
О
для устойчивости системы не-
обходимо и достаточно выполнения следующих условий:
II* ^
01 <к
а
2
А1
= > 0; Д
2
=
>0; Д.
ay а
3
а
ъ
а
2
а^
0 а
г
а
3
0;
в О о
'ГС
aj
«
... 0
а
о
«2
... 0
0
а
г
а
3
... 0
0
0
0
• • • а^
• (3.40)
>

Раскрывая, например, определители Гурвица для характе-
ристических уравнений первого, второго, третьего и четвер-
того порядков, можно получить следующие условия устойчи-
вости:
1) для уравнения первого порядка (п = 1), т. е. а
0
s +
+ а
г
= 0, условия устойчивости
а
0
>0; % > 0; (3.41)
2) для уравнения второго порядка (п = 2), т. е. a
0
s
2
+
+ а
2
= 0, условия устойчивости
a
Q
> 0; а
г
> 0; а
2
>0; (3.42)
3) для уравнения третьего порядка (п ~ 3), т. е. а
0
$* +
+ djf + a
2
s + а
ц
= 0, условия устойчивости
a
Q
> 0; щ > 0; а
2
> 0; a
s
> 0; (3.43)
а
г
а
2
— а
(
/х
3
> 0; (3.44)
4) для уравнения четвертого порядка 4), т . е. а^ +
+a
1
s
3
+ аф
9
" + .аф + 0, условия устойчивости
«о>0; а
а
>0; а
г
> 0; а
4
>0; (3.45)
Оз а
2
—а
0
а
3
) —а
4
> 0. (3.46)
Таким образом, необходимым и достаточным условием ус-
тойчивости для систем первого и второго порядков является
положительность коэффициентов характеристического уравне-
ния. Для уравнения третьего и четвертого порядков кроме по-
ложительности коэффициентов необходимо соблюдение допол-
нительных неравенств (3.44) и (3.46).
При п
Г^г
5 число подобных дополнительных неравенств
возрастает, процесс раскрытия определителей становится до-
вольно трудоемким и громоздким. Поэтому критерий устой-
чивости Гурвица обычно применяют при п ^ 4. При п ^ 5 це-
лесообразно применять формулируемый ниже критерий устой-
чивости Льенара — Шипара либо при использовании крите-
рия устойчивости Гурвица переходить к численным методам с
использованием ЭВМ.
В последнем столбце главного определителя Гурвица (3.38)
отличен от нуля только один коэффициент а
п%
поэтому
A
n
=fln^ (
3
-47)

Из (3.47), видно, что при а^ > 0 для проверки устойчивости
системы достаточно найти только определители Гурвица от А
г
до An-i. Если все определители Гурвица низшего порядка
положительны, то система находится на границе устойчиво-
сти, когда главный определитель равен нулю:
А* —
а
п An-i- (3.48)
Последнее равенство возможно в двух случаях: а
п
= 0 или
А
п
— О. В первом случае система находится на границе
апериодической устойчивости (один из корней характеристи-
ческого уравнения равен нулю); во втором случае — на гра-
нице колебательной устойчивости (два комплексно-сопряжен-
ных корня характеристического уравнения находятся на мни-
мой оси).
Используя критерий Гурвица, можно при заданных пара-
метрах системы принять за неизвестный какой-либо один
параметр (например, коэффициент усиления, постоянную вре-
мени и т. д. ) и определить его предельное (критическое) зна-
чение, при котором система будет находиться на границе ус-
тойчивости.
Следует заметить, что критерий Гурвица можно получить
из критерия Рауса, поэтому иногда критерий Гурвица называ-
ют критерием Рауса — Гурвица.
Критерий устойчивости Льенара — Шипара» Для иссле-
дования устойчивости систем автоматического управления,
имеющих порядок характеристического уравнения п ^ 5,
удобно применять одну из модификаций алгебраического кри-
терия устойчивости Гурвица, предложенную в 1914 г. П, Лье-
наром и Р. Шипаром.
Доказано, что в том случае, когда все коэффициенты харак-
теристического уравнения (3.30) положительны (а
0
> 0, а
г
>
>0, а
п
> 0), из того факта, что положительны все оп-
ределители А
1г
Д
3
, А
5
,... с нечетными индексами, следует и
положительность определителей А. Гурвица А
2
, Д
4
, А
6
, ...
с четными индексами, и наоборот.
Поэтому в тех случаях, когда выполнены необходимые усло-
вия устойчивости, т. е. а
0
>0, £^>0,..., а
п
>0,
необходимые
и
достаточные условия устойчивости сводятся к тому, чтобы
среди определителей Гурвица А
и
А
2
, А
п
были положитель-
ны все определители с четными (или
же все
определители с не-
четными) индексами.

Таким образом, для того чтобы система автоматического
управления была устойчива, необходимо и достаточно, чтобы
выполнялись следующие неравенства:
а
0
>
О,
^>0, ..., а
п
> 0,
Ai>0, Д
3
>0, Л
5
>0,
или
а
0
>
О,
а
х
>0, а
п
> 0,
Д
2
>0
5
Д
4
>0, А
е
>0, ....
(3.49)
(3.50)
Последняя формулировка критерия устойчивости, называе-
мая критерием устойчивости Льеиара — Шипара, требует
раскрытия меньшего числа определителей, чем обычный кри-
терий Гурвица, а поэтому особенно удобна при исследовании
устойчивости систем автоматического управления высокого
порядка.
Пример 3.2» Пусть характеристическое уравнение системы D (s) —
= 12s
4
+ 2s
2
+ 4s -f- 50 = 0. Система неустойчива, так как коэффи-
циент а
г
= 0.
Пример З.З. Характеристическое уравнение системы D (s) = 3s
5
+
+ 10s
4
+ 5s
3
— 7s
2
+ s + 100 — 0. Система неустойчива, так как
—7 < 0.
Пример 3.4. Характеристическое уравнение системы D (s) =
= 2s
3
+ 6s
2
+ 10s + 15 = 0. Все коэффициенты этого характеристиче-
ского уравнения положительны, и определитель Гурвица А
2
с четным
индексом равен
а
г
а
3
сю
а
2
=
с
2
—
а
о
а
3
= е>-10 —
2»
15—
30
>0.
Следовательно, система устойчива.
Пример 3.5. Характеристическое уравнение системы
D (s) - (1 + T
lS
) (1 + T
2
s) (1 + T
3
s) + К = 0,
где К — коэффициент усиления разомкнутой системы; T
lt
T
2S
Т
3
—
постоянные времени отдельных динамических звеньев системы. Найдем,-
пользуясь критерием Гурвица, предельное значение коэффициента уси-
ления разомкнутой системы /<
К11
как функцию постоянных времени
^2» ЗГ
8
.
Перепишем характеристическое уравнение в виде
D
(s)
= Т
г
Т
2
Т
Ф
* + (Т
г
Т
2
+ Т
г
Т
3
+ Т
2
Т
3
)
s
2
+ (Т
г
+ Т
2
+ Т
8
) s+
+
1
+ К =
a
Q
s?
+
aiS
2
+
a
2
s
+ а
3
= 0,
где
Яо
= ПТ
2
Т
3
; а
г
- Т
г
Т
2
+ Т
г
Т
3
+ Т
2
Т
3
; а
2
= Т
г
+ Т
2
+ Т
3
;
а
3
= 1 + К-

Согласно критерию устойчивости Гурвица, система третьего поряд-
ка будет устойчива, если выполняются следующие неравенства:
аа > 0; ^ > 0, а
2
> 0, a
z
> 0, а
г
а
2
— а
0
а
3
> 0.
В данном случае все коэффициенты характеристического уравне-
ния положительны, поэтому система будет устойчива, если
(Т
г
Т
2
+ Т
г
Т
г
+ Т
2
Т
3
) (Т
г
+ Г
2
+ Т
3
) > Т
г
Т
2
Т
в
(1 + К).
Последнее неравенство можно переписать в виде
К < (1 + т
2
+ т
3
) (I + 1/т
2
+ 1/TJ) - 1,
где _ / __
т
2
— TJTi, т
3
=
Предельное (критическое) значение коэффициента усиления, при
котором система будет находиться на границе устойчивости, равно
К*р = (1 + V+
т
з) (1 + 1/т. + ~ 1.
Из последнего выражения следует, что предельный коэффициент
усиления системы определяется ие абсолютными значениями постоянных
времени динамических звеньев, а их относительными значениями. Чем
более резко отличаются постоянные времени друг от друга, тем больше
/£
к
р- В частном случае, когда т
а
= т
а
= 1, т. е. Т
г
— Т
2
— Т
3
, зна-
чение /Скр минимально и равно всего лишь К
кр
~ 8.
§ 3.6. Частотные критерии устойчивости
Частотные критерии устойчивости позволяют судить об ус-
тойчивости систем автоматического управления по виду их
частотных характеристик. Эти критерии являются графоана-
литическими и получили широкое распространение, так как
позволяют сравнительно легко исследовать устойчивость сис-
тем высокого порядка, а также имеют простую геометричес-
кую интерпретацию и наглядность.
Принцип аргумента. В основе частотных критериев устой-
чивости лежит следствие из известного в теории функций ком-
плексного переменного принципа аргумента, который кратко
излагается ниже.
Пусть дан некоторый полином п-й степени D (s) — a
0
s
n
+
+ ... + а
п
. Этот полином в соответствии с теоремой
Безу можно представить в виде D (s) = а
0
(s — s
t
) (s — s
2
)...
... (s — s
n
), где $i = a
t
+ /со^ — корни уравнения'и (s) == 0.
На комплексной плоскости s каждый корень геометрически
может быть изображен вектором, проведенным из начала ко-
ординат к точке Si (рис. 3.6, а). Длина этого вектора равна
модулю комплексного числа s
i9
т. е. |s$|, а угол, образован-

ный вектором с положительным направлением действитель-
ной оси, — аргументу или фазе комплексного числа s
i7
т. е.
Arg s*.
Величины (s — s
t
) геометрически изображаются векторами,
проведенными из точки s
t
к произвольной точке s (рис. 3.6, б).
В частном случае при s = /со получим
D (/со) = а
0
(/со — s
x
) (/со — s
3
), (/со — s
n
). (3.51)
Концы элементарных векторов (/со — Sj) будут находиться
на мнимой оси в точке s = /со (рис. 3.6, в).
В выражении (3.51) D (/со) представляет собой вектор,
равный произведению элементарных векторов (/to — s$) и дей-
ствительного числа а
0
.
Модуль этого вектора равен произведению модулей эле-
ментарных векторов и а
0
:
|D (/со) I — а
0
|/со — Stll /со — s
2
|...| /со — s
ft
|
f
(3.52)
а аргумент или фаза его равна сумме аргументов элементарных
векторов:
Arg D (/со) = Arg (/со — sO + Arg (/со — s
2
)+...+
Условимся считать вращение против часовой стрелки по-
ложительным. Тогда при изменении со от — оо до оо каждый
элементарный вектор повернется на угол я, если его начало,
т. е. корень s
t
, расположено слева от мнимой оси, и на угол
— я, если корень расположен справа от мнимой оси (рис. 3.7).
Предположим, что полином D (s) имеет т правых корней и
п — т левых.
+ Arg (/со — s
n
).
(3.53)
5) jw б)
Рис. 3.6
