Воронов А.А. Теория автоматического управления. Часть первая

Подождите немного. Документ загружается.

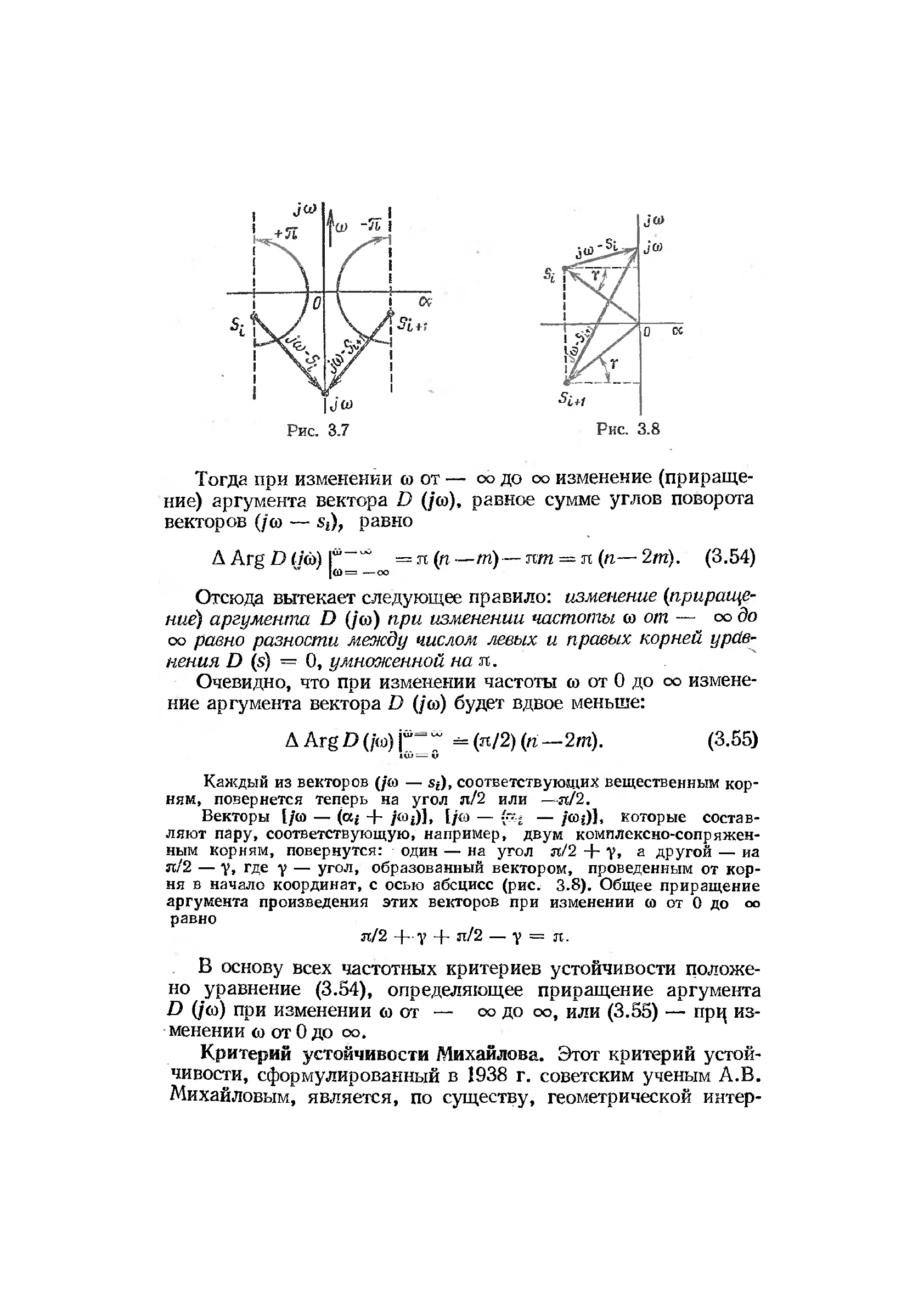
Тогда при изменении

со

от — оо до оо изменение (прираще-

ние) аргумента вектора D (/со), равное сумме углов поворота

векторов (/со — Si), равно

Arg D

Uсо) —

(п

—

т) —

пт = п (ft— 2т). (3.54)

[©=: —ОО

Отсюда вытекает следующее правило: изменение (прираще-

ние) аргумента D (/со) при изменении частоты со от — оо до

оо равно разности между числом левых и правых корней урав-

нения D (s) — 0, умноженной на п.

Очевидно, что при изменении частоты со от 0 до оо измене-

ние аргумента вектора D (/со) будет вдвое меньше:

Arg D

(До)

^ (л/2) (rt—2m). (3.55)

Каждый из векторов (/{о — s^), соответствующих вещественным кор-

ням, повернется теперь на угол л/2 или —я/2.

Векторы [/со — (щ + /ЧЙ

)], [/со — — /со,;)], которые состав-

ляют пару, соответствующую, например, двум комплексно-сопряжен-

ным корням, повернутся: один — на угол л/2 + у, а другой — иа

л/2 — у,

Де Y — угол, образованный вектором, проведенным от кор-

ня в начало координат, с осью абсцисс (рис. 3.8). Общее приращение

аргумента произведения этих векторов при изменении со от 0 до оо

равно

л/2 + у + л/2 — у = я.

В основу всех частотных критериев устойчивости положе-

но уравнение (3.54), определяющее приращение аргумента

D (/со) при изменении

<о

от — оо до оо, или (3.55) — прц из-

менении

от 0 до оо.

Критерий устойчивости Михайлова. Этот критерий устой-

чивости, сформулированный в 1938 г. советским ученым А.В.

Михайловым, является, по существу, геометрической интер-

претациёй принципа аргз'мента и позволяет судить об устой-

чивости системы на основании рассмотрения некоторой кри-

вой, называемой кривой Михайлова.

Пусть дано характеристическое уравнение системы (3.30).

Левую часть характеристического уравнения называют ха-

рактеристическим полиномом

(s)

+ a

+ ... + a

. (3.56)

Если подставить в этот полином чисто мнимое значение

s = /со, то получим комплексный полином

(/со)

- а

(/со)"+а

(/со)"-

+ ... + a

- X

(со)

+ / Y

(ш)

-J9(co)e^^>, (3.57)

где

(со) —

-а

—2

со

—...,

Г(а>) =©(a

-i. — a

~ ...)J

(3.58)

называют соответственно вещественной и мнимой функциями

Михайлова; функции D (со) и

-ф

(со) представляют собой мо-

дуль и. фазу (аргумент) вектора D (/со).

При изменении частоты со вектор D (/со), изменяясь по ве-

личине и направлению, будет описывать своим концом в ком-

плексной плоскости некоторую кривую, называемую кривой

(годографом) Михайлова.

В соответствии с (3.55) угол поворота вектора D (/со) вок-

руг начала координат при изменении частоты со от 0 до оо ра-

вен

4 Arg D (/со) (п -2т).

Отсюда определяем число правых корней полинома D (s),

т. е.

™/2-А Arg Р (;«,) [-У ,

Из (3.59) видно, что число правых корней т будет равно нулю

при одном-единственном условии

Arg

D(/со) \%Zo

- т/2. (3.60)

Условие (3.60) является необходимым, но не достаточным

условием устойчивости. Для устойчивости системы необходи-

мо и достаточно, чтобы все п корней характеристического урав-

нения были левыми; иначе говоря, среди них не должно быть

корней, лежащих на мнимой оси и обращающих в нуль комп-

лексный полином D (/&>), т. е. должно выполняться еще одно

условие

В (/чо) Ф-0. (3.61)

Формулы (3.60) и (3.61) представляют математическое выра-

жение критерия устойчивости Михайлова: для того чтобы си-

стема автоматического управления была устойчива, необхо-

димо и достаточно, чтобы вектор кривой Михайлова D

(/о>)

при изменении со от 0 до оо повернулся, нигде не обращаясь в

нуль, вокруг начала координат против часовой стрелки на,

угол ад/2, где п — порядок характеристического уравнения.

Заметим, что для устойчивых систем кривая Михайлова на-

чинается при со = 0 на вещественной положительной полуоси,

поскольку при а

> 0 все коэффициенты характеристического

уравнения положительны и D(0) = а

> 0. Кроме того, для

устойчивых систем, описываемых обыкновенными дифферен-

циальными уравнениями с постоянными коэффициентами, фа-

за (аргумент)

я£)

(о>) с ростом частоты со должна возрастать мо-

нотонно, т. е вектор D (/со) должен поворачиваться только

против часовой стрелки, поскольку с ростом частоты монотон-

но возрастают имеющие одинаковые (положительные) знаки

фазы элементарных векторов (/со s*)

являющиеся слагаемы-

ми фазы вектора £>(/со) (см. (3.53)).

Учитывая сказанное выше, критерий устойчивости Михай-

лова можно сформулировать так: для того чтобы система ав-

томатического управления была устойчива, необходимо и до-

статочно, чтобы кривая

(годограф)

Михайлова при изменении

частоты

со

от 0 до оо, начинаясь при ш — 0 на вешрственной

положительной полуоси, обходила только против часовой

стрелки последовательно п квадрантов координатной плос-

кости, где п — порядок характеристического уравнения„

Кривая Михайлова для устойчивых систем всегда имеет

плавную спиралевидную форму, причем конец ее уходит в

бесконечность в том квадранте координатной плоскости, но-

мер которого равен степени характеристического уравнения.

На рис. 3.9 показаны типичные кривые Михайлова для

устойчивых систем, описываемых уравнениями, начиная от

первого (п — 1) и кончая пятым (п = 5) порядком. Для удоб-

ства сравнения коэффициенты

ВО

всех случаях приняты оди-

наковыми.

Признаком неустойчивости системы является нарушение

числа и последовательности пройденных кривой Михайлова

квадрантов координатной плоскости, вследствие чего угол по-

ворота вектора D (/со) оказывается меньше, чем пп/2. Число

правых корней неустойчивой системы можно определить по

(3.59).

На рис. ЗЛО показаны кривые Михайлова для неустойчи-

вых и нейтральных систем. Рис. ЗЛО, а — при ш — 0 кривая

Михайлова начинается на отрицательной вещественной полу-

оси; система неустойчива. Рис. ЗЛО, б — порядок уравнения

п = 5, а кривая Михайлова находится вся в одном квадран-

те (этому соответствует характеристическое уравнение D (s)=

— a

+ a

+ — 0)з система неустойчива. Рис. ЗЛО, в —

нарушена последовательность прохождения квадрантов; сис-

тема неустойчива. Рис. 3.10, г—кривая Михайлова начинает-

ся в начале координат, т. е. в характеристическом уравне-

нии имеется по крайней мере один нулевой корень; система

находится на границе апериодической устойчивости; неболь-

шая деформация кривой Михайлова (прерывистая линия) де-

лает систему устойчивой. Рис. ЗЛО, д — кривая Михайлова

г/роходит при некотором значении частоты ш

через начало

координат, т. е. в характеристическом уравнении имеются

чисто мнимые корни ± /со*.; система находится на границе ко-

лебательной устойчивости; небольшая деформация кривой

Михайлова делает систему устойчивой (прерывистая линия).

Рис. ЗЛО, е — кривая Михайлова проходит через начало ко®

ординат, но небольшой деформацией кривой Михайлова удов-

летворить условиям устойчивости нельзя; система неустойчи-

ва.

Построение кривой Михайлова практически производится

либо методом контрольных точек, либо методом вспомогатель-

ных годографов. Первый метод

сводится к определению ряда то-

чек кривой Михайлова, соответ-

ствующих фиксированным значе-

ниям частоты о* включая (обяза-

тельно) частоты точек пересечения

кривой с осями координат, кото-

рые находятся как корни уравне-

ний (3.62) и (3.63). При втором

методе предварительно определяют

годографы отдельных звеньев си-

Рис. 3.9 стемы и по ним строят искомую

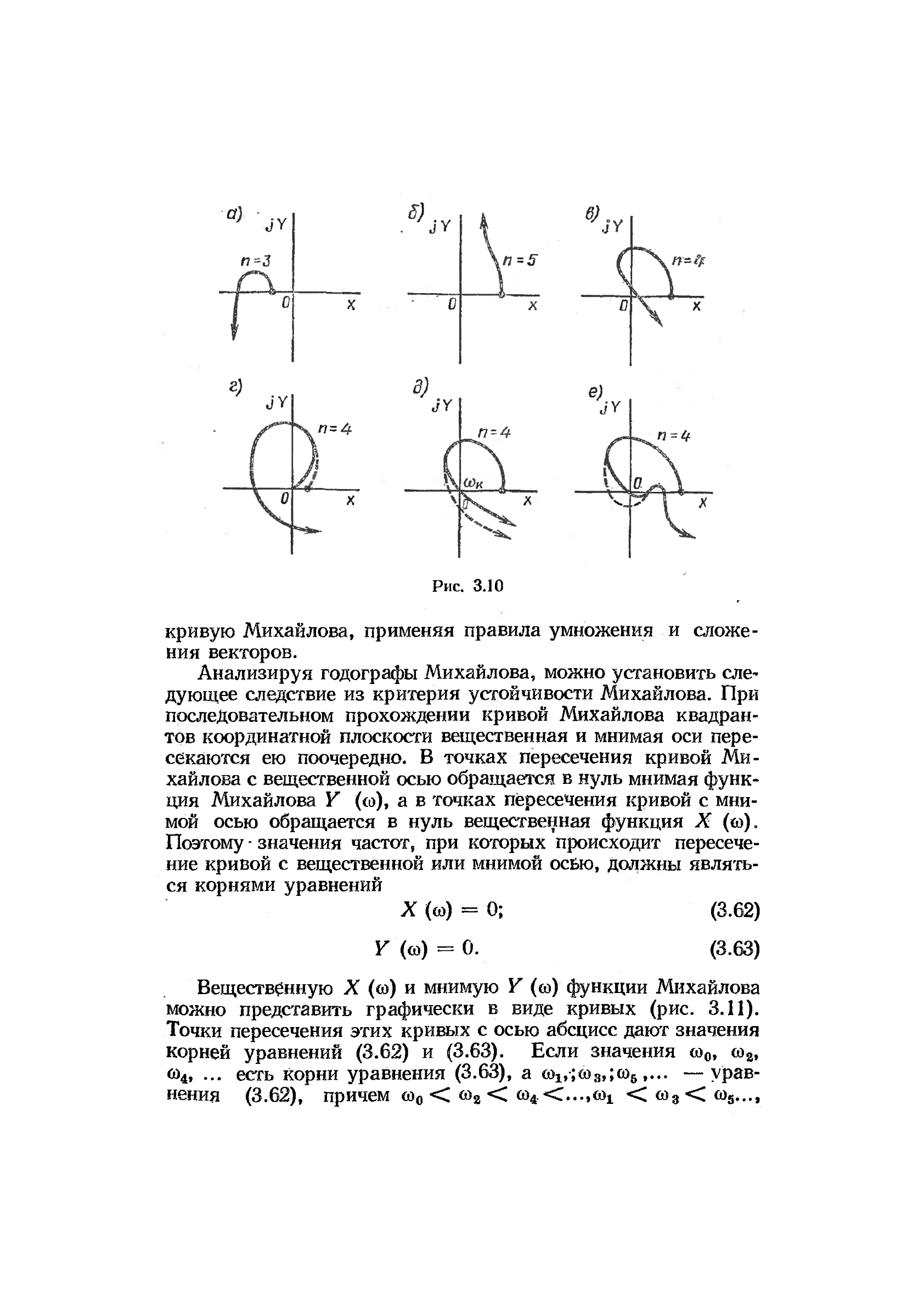
Рис. 3.10

кривую Михайлова, применяя правила умножения и сложе-

ния векторов.

Анализируя годографы Михайлова, можно установить сле-

дующее следствие из критерия устойчивости Михайлова. При

последовательном прохождении кривой Михайлова квадран-

тов координатной плоскости вещественная и мнимая оси пере-

секаются ею поочередно. В точках пересечения кривой Ми-

хайлова с вещественной осью обращается в нуль мнимая функ-

ция Михайлова У (со), а в точках пересечения кривой с мни-

мой осью обращается в нуль вещественная функция X (со).

Поэтому

значения частот, при которых происходит пересече-

ние кривой с вещественной или мнимой осью, должны являть-

ся корнями уравнений

X (со) = 0; (3.62)

К (со) - 0. (3.63)

Вещественную X (со) и мнимую Y (со) функции Михайлова

можно представить графически в виде кривых (рис. 3.11).

Точки пересечения этих кривых с осью абсцисс дают значения

корней уравнений (3.62) и (3.63). Если значения со

, со

оз

, ... есть корни уравнения (3.63), a oo

;(x)

;(o

,...

— урав-

нения (3.62), причем со

< о>

< Щ <а>

<со

...,

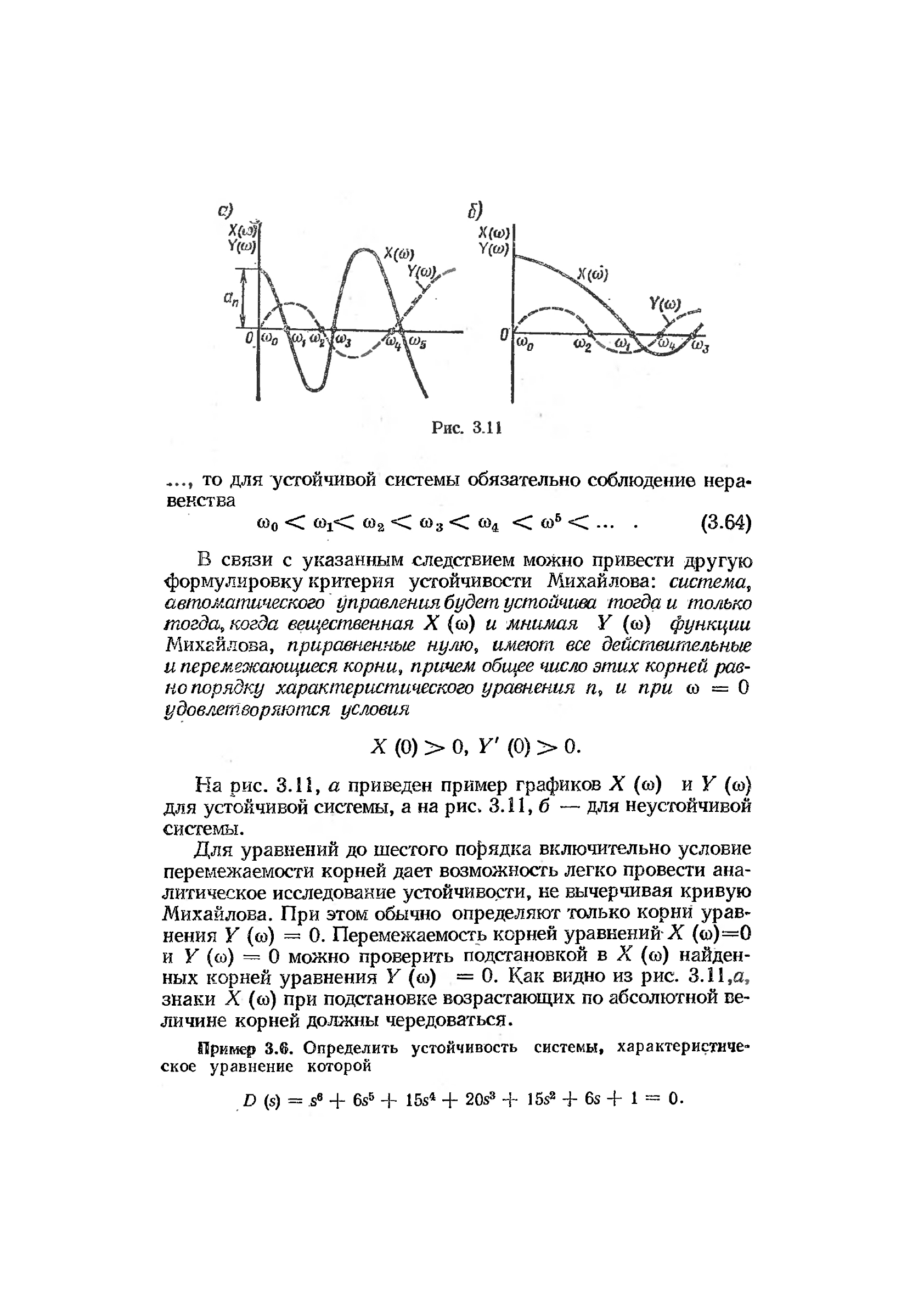
то для устойчивой системы обязательно соблюдение нера-

венства

со

< щС со

< о)

< щ < о)

< ... . (3.64)

В связи с указанным следствием можно привести другую

формулировку критерия устойчивости Михайлова: система,

автоматического управления

будет устойчива

тогда и только

тогда, когда вещественная X (со) и мнимая Y (со) функции

Михайлова, приравненные нулю, имеют все действительные

перемежающиеся

корни, причем

общее число

этих корней рав-

но порядку характеристического уравнения

п>

и при со = О

удовлетворяются условия

X (0) > 0, Y' (0) > 0.

На рис. З.П, а приведен пример графиков X (со) и Y (со)

для устойчивой системы, а на рис. 3.11, б — для неустойчивой

системы.

Для уравнений до шестого порядка включительно условие

перемежаемости корней дает возможность легко провести ана-

литическое исследование устойчивости, не вычерчивая кривую

Михайлова. При этом обычно определяют только корни урав-

нения Y (со) = 0. Перемежаемость корней уравнений X (со)=0

и У (со) = 0 можно проверить подстановкой в X (со) найден-

ных корней уравнения Y (со) = 0. Как видно из рис. 3.11

знаки X (со) при подстановке возрастающих по абсолютной ве-

личине корней должны чередоваться.

Пример 3.6. Определить устойчивость системы, характеристиче-

ское уравнение которой

D(s) = s

+ 6s

+ 15s

+ 20s

+ 15s

+ 6s + 1 = 0.

Подставляем s = /со и находим вещественную и мнимую функции Ми-

хайлова:

X (со) = —со

+ 35со

— 15со

+1 = 0;

У (со) = со (бсо

— 20со

+ 6) = 0.

Находим корни уравнений У (со) = 0, т. е. со

= 0; со

— 3,33co

+1=0, откуда

coi

= 3,67 ± Т/2,78—1; со|=0,36; со!=2,96.

Если перемежаются корни, то перемножаются и их квадраты, по-

этому нахождение со

и со

не обязательно.

Проверим, чередуются ли знаки X (со) при подстановке со| и со|.

Имеем

х (С0

) = — 0,36

+ 15-0,36

— 35*0,36 + 1 = —2,51;

X (со

) = —2,96* + 15-2,96

— 15-2,96 + 1 > 0.

Так как все корни У (со) вещественны и знаки ординат X (со),

соответствующие этим корням, чередуются, то система устойчива.

Критерий устойчивости Найквиста. Этот частотный крите-

рий устойчивости, разработанный в 1932 г. американским уче-

ным Г. Найквистом, позволяет судить об устойчивости замкну-

той системы по виду амплитудно-фазовой характеристики ра-

зомкнутой системы.

Пусть передаточная функция разомкнутой системы

W(s)Ailt^r^-^^

. (3.65)

Q(s) c

^+c

+...+Cn

Подставляя в (3.65) s — /со, получает частотную передаточ-

ную функцию разомкнутой системы:

w (/СО) -

R (/0))

-- М/О>)

+ МУЕО )

+ ...+*Т

Q (/®> (/со)" + с

(/o))

rt 1

+ ... +

= и И + jV (со) = А (со) е*К®>, (3.66)

где U (со) и Y

(со)

— действительная и мнимая части частот-

ной передаточной функции соответственно; модуль А (со) и

фаза яр (со) частотной передаточной функции равны А (со) =

- УТ/

ЩГ+ I/

(со); яр (<о) = Arctg Щ.

Если изменять частоту со от —оо до оо, то вектор W (/со)

будет меняться по величине и фазе. Кривую, описываемую кон-

цом этого вектора в комплексной плоскости, называют ампли-

тудно-фазовой характеристи-

кой разомкнутой системы

(рис. 3.12).

Амплитудно-фазовая харак-

теристика симметрична относи-

тельно вещественной оси, поэто-

му обычно вычерчивают только

ту часть ее, которая соответст-

вует положительным частотам

есС>0 (сплошная линия на рис.

3.12), а ветвь этой характеристи-

ки, соответствующая отрица-

тельным частотам

со

(пунк-

тирная линия на рис. 3.12), может быть найдена как зеркаль-

ное отражение ветви, соответствующей положительным часто-

там, относительно вещественной оси.

Рассмотрим вспомогательную функцию

Ф (s) = 1 + W (s) = 1 + R (s)/Q (s) = [Q (s) + R (s)V

/Q (s), - D (s)/Q (s), (3.67)

где D (s) = Q (s) + R (s) = a

+ a^'

+ ... + a

—

характеристический полином. замкнутой системы; Q (s) =

= c

+ CxS"-

+ ... + c

— характеристический полином

разомкнутой системы; R (s) — s

+ Ь

+ ... + b

—

— полином степени т.

Заметим, что так как в реальных системах степень полико-

ма R (s) не выше степени полинома Q (s), т. е. m ^

п>

то сте-

пени числителя и знаменателя дроби (3.67) одинаковы и рав-

ны п.

Подставляя в (3.67) s = /со, получим

Ф (/со) - 1 + W (/со) - [Q

(/©)

+ R(fa№(j<») = D (j(*)/Q (/со).

(3.68)

Пусть характеристическое уравнение замкнутой системы

£> (s) — 0 имеет т правых корней и п—т левых корней, а ха-

рактеристическое уравнение разомкнутой системы Q

($)

= О

имеет I правых и п — I левых корней.

При изменении частоты со от

— оо

до оо изменение угла по-

ворота вектора ф (/Ъ) на основе принципа аргумента будет

AArg

ц (/со) |ю~!1со

Arg D

(/со) —Д

ArgQ

(/со)

=п

[(п

—т) —т] —п

[(п

—I)—1\ = 2я

(I —/п).

(3.69)

W (jo))

и (О)}

Рис. 3.12

Для устойчивости замкнутой системы необходимо и доста-

точно, чтобы все корни ее характеристического уравнения

были левыми, т. е. т=^0. Отсюда суммарный поворот

вектора <р (/со) устойчивой системы вокруг начала координат

должен быть равен

Д Arg

ср (/со)

ft™ -

2п1,

(3.70)

где I — число правых корней характеристического уравнения

разомкнутой системы.

Обычно рассматривают только положительные частоты

со

> 0, в этом случае угол поворота вектора <р(/со) будет вдвое

меньше, т

е.

Д Argcp

(/со)

\%=о «nl - 2зт//2. (3.71)

Таким образом, если разомкнутая система является неус-

тойчивой и имеет I правых корней, то замкнутая система будет

устойчива тогда и только тогда, когда амплитудно-фазовая ха-

рактеристика вспомогательной функции ф (/со) при изменении

частоты со от 0 до со охватывает начало координат в положи-

тельном направлении 1/2 раз.

Легко заметить, что число оборотов вектора <р (/со) вокруг

начала координат равно числу оборотов вектора W (/со) во-

круг точки (—1, /0).

На основании сказанного вытекает следующая формулиров-

ка критерия устойчивости Найквиста: если разомкнутая сис-

тема автоматического управления неустойчива, то, для того

чтобы замкнутая система автоматического управления была

устойчива, необходимо и достаточно, чтобы амплитудно-фа-

зовая характеристика разомкнутой системы W (/со) при из-

менении частоты со от 0 до оо охватывала точку (—1, / 0)

в положительном направлении

112,

раз

где I — число правых

корней характеристического уравнения разомкнутой системы.

На рис. ЗЛЗ, а показана амплитудно-фазовая характеристи-

ка <р (/со), а на рис. ЗЛЗ, б — амплитудно-фазовая характе-

ристика W (/о), соответствующие устойчивой замкнутой сис-

теме, которая в разомкнутом состояний была неустойчива и

имела число правых корней / = 2. Обычно в реальных систе-

мах W

(/со) Jo) — со

= О, и поэтому ф (/со) 1(0=

ео

= 1.

При сложной форме характеристики W (/со) могут возник-

нуть затруднения при определении числа ее оборотов вок-

руг критической точки (—I, /0). В этом случае для суждения

об устойчивости удобно применять «правило переходов», пред-

ложенное Я. 3. Цыпкиным.

Назовем переход характеристики W (/со) через отрезок ве-

щественной оси слева от точкц (—1, /0), т. е. через отрезок

(—оо, —1), при возрастании со положительным, если он про-

исходит сверху вниз, и отрицательным, если он происходит

снизу вверх. Если характеристика W (/со) начинается на отрез-

ке (— оо, —1) при со = 0 или заканчивается на нем при со =

= оо, то в этих случаях считают, что она совершает полпере-

хода.

Тогда критерий Найквиста можно сформулировать так:

если разомкнутая система автоматического управления не-

устойчива, то, для того

чтобы

замкнутая

система

автомати-

ческого

управления была устойчива, необходимо и достаточно,

чтобы разность между числом положительных и отрицатель-

ных переходов амплитудно-фазовой характеристики разомк-

нутой системы W (/со) через отрезок

вещественной

оси (— оо,

—1) при изменении частоты

<о

от 0 до

оо

была равна 1/2, где

•—

число правых корней характеристического уравнения ра-

зомкнутой системы.

Если система автоматического управления в разомкнутом

состоянии устойчива, т. е. I = 0, то приращение аргумента

вектора ср (/со) равно нулю:

Д Arg

ф (/со) ос

2п1

= 0. (3.72)

Это означает, что для устойчивости замкнутой системы не-

обходимо, чтобы амплитудно-фазовая характеристика ф (/со)

не охватывала начало координат (рис. 3.14, а), а амплитудно-

фазовая характеристика W (/со) не охватывала точку с коорди-

натами (—1, /0), (рис. 3.14, б).

Таким образом, для этого наиболее часто встречающегося

на практике случая получаем следующую формулировку кри-

терия Найквиста: если разомкнутая система

автоматическо-

го управления устойчива, то замкнутая

система автоматичес-

Рис. 3.13