Воронов А.А. Теория автоматического управления. Часть первая

Подождите немного. Документ загружается.

Передаточная функция разомкнутой системы с запаздыва-

нием равна

(S)

= ^вап fr) W (s) = ^TT

$Т

> <

)

(s)

где W (s) = R (s)/Q (s) — передаточная функция разомкнутой

системы без учета запаздывания, представляющая собой дроб-

но-рациональную функцию оператора s.

Заметим, что если в одноконтурной системе имеется не-

сколько последовательно соединенных запаздывающих звень-

ев, то они могут быть заменены одним запаздывающим звеном

с эквивалентной постоянной времени запаздывания, равной

сумме всех постоянных времен запаздывания.

Если запаздывающее звено находится в прямой цепи, то

передаточная функция замкнутой системы

Wg* (Р) - Т^ГТТ = ^

(S)e ST

= ^(s)/Dx (S). (3,96а)

Если же запаздывающее звено находится в цепи обратной

связи, то передаточная функция замкнутой системы

——

(

з.9бб)

I + W

(s) Q(s)+*(s)e~

ls)

№ (3,96a) и (3-966) видно, что независимо от места включе-

ния запаздывающего звена характеристическое уравнение сис-

темы с запаздыванием и^геет вид

(s)

Q{s)

+ R

(s)

е-

* - 0. (3.97)

Это характеристическое уравнение из-за наличия множите-

ля e~

является не полиномом, а трансцендентной функцией

оператора s и в отличие от обыкновенного алгебраического

уравнения имеет бесконечное множество корней. Так как

, , S

X»

= 1 — ST Н F-...,

2! 3!

то (3.97) можно рассматривать как уравнение «бесконечной

степени».

Для того чтобы линейная система с постоянным запазды-

ванием была устойчива, необходимо и достаточно, чтобы все

корни уравнения (3.97) были левыми. Нахождение корней

уравнения (3.97) затруднительно, поэтому для исследования

устойчивости систем с запаздыванием используют критерии

устойчивости.

Следует иметь в виду, что алгебраические критерии устой-

чивости Рауса и Гурвица в их обычной форме для исследования

систем с запаздыванием непригодны, причем для устойчивости

линейных систем первого и второго порядков с запаздыванием

только положительности коэффициентов характеристическо-

го уравнения уже становится недостаточно. Существуют раз-

личные алгебраические критерии устойчивости для систем

с запаздыванием, которые являются аналогами крите-

риев Рауса и Гурвица, однако в инженерной практике они

широкого применения не нашли из-за их относительной слож-

ности.

Для исследования устойчивости систем с запаздыванием

можно применять основанные на принципе аргумента частот-

ные критерии устойчивости Михайлова и Найквиста либо ме-

тод D-разбиения-.

Уравнение кривой (годографа) Михайлова системы с запаз-

дыванием получают после подстановки s = /со в характеристи-

ческое уравнение (3.97), т. е.

(/со,

/Чот

) =

Q (/со)

+ R

(/со)

е~ ^ =

(3.98)

Наличие в (3.98) множителя делает очертания кри-

вой Михайлова достаточно сложными, и формулировка этого

критерия для систем с запаздыванием становится не такой про-

стой, как для обычных систем. Как показал Я. 3. Цыпкин, для

исследования устойчивости систем с запаздыванием очень

удобно применять критерий устойчивости Найквиста.

Заключение об устойчивости замкнутой системы с запазды-

ванием делается на основании исследования поведения ампли-

тудно-фазовой характеристики W

(/о) разомкнутой системы

с запаздыванием относительно точки (—1, /0). Формулировка

критерия устойчивости Найквиста для систем с запаздыва-

нием в этом случае аналогична формулировке для обычных

систем, имеющих дробно-рациональные передаточные функции.

Частотную передаточную функцию W

(/со) разомкнутой

системы с запаздыванием находят, подставляя s

—

/со в (3.95):'

(/со)

- W

(/со)

е-'<°

- А

(со) ©*<«>

е-'"

>т

= Л(со)е'^

<С0)

, (3.99)

где W (/со) — U

(со)

+ jV (со) — амплитудно-фазовая харак-

теристика разомкнутой системы без учета запаздывания;

А (со) = | W </co)| (со) + V

(со) —амплитудно-частот-

V (со)

ная характеристика;

я|>

(w) — Arctg ^^ — фазочастотная ха-

рактеристика разомкнутой системы без учета запаздывания;

я|>

(со) ф (со) — сот (3,100)

— фазочастотная характеристика разомкнутой системы с за-

паздыванием.

Из (3.99) и (3.100) видно, что наличие запаздывающего зве-

на не меняет модуля А (со) амплитудно-фазовой характери-

стики разомкнутой системы W (/(о), а вносит лишь дополни-

тельный отрицательный фазовый сдвиг от, пропорциональный

частоте, причем коэффициентом пропорциональности являет-

ся время запаздывания т.

Зная амплитудно-фазовую характеристику W (/со) разом-

кнутой системы без запаздывания, легко

построить амплитуд-

но-фазовую характеристику И^

(/ш) разомкнутой системы с за-

паздыванием. Для этого каждый модуль А (со

) вектора ам-

плитудно-фазовой характеристики W (/со) нужно повернуть на

угол со

-т по часовой стрелке. С ростом частоты со угол сот

будет быстро расти, а модуль А (со) обычно уменьшается, по-

этому амплитудно-фазовая характеристика W

(jw) разомкну-

той системы с запаздыванием имеет вид спирали, закручиваю-

щейся вокруг начала координат (рис. 3.31). «Закручивание»

амплитудно-фазовой характеристики из-за наличия дополни-

тельного фазового сдвига сот, вообще говоря, ухудшает усло-

вие устойчивости, так как вся амплитудно-фазовая характе-

ристика приближается к критической точке (—1, /0). Однако

иногда при сложной форме амплитудно-фазовой характери-

стики W (/со) введение постоянного запаздывания может улуч-

шить условия устойчивости.

Изменяя время запаздыва-

ния т в широких пределах,

можно найти такое его зна-

чение, при котором замкну-

тая система будет находить-

ся на границе устойчивости.

этом случае характери-

стика W

(/со) будет прохо-

дить через точку (—1,/0).

Время запаздывания т

кр

соответствующее ему значе-

ние частоты со

р, при кото-

-ио{

ьуг-R

V к'

w=0

О),

6)1

^(ja)

Рис. 3.31

рых

(/со) проходит через точку

(—1

,/0), называют крити-

ческими.

Для критического случая справедливо следующее условие:

(/со

кр

;

- W

(/со

кр

)

е-

/ш

ир V = д

(со

кр

) е'"

W^P)~Vkp] =

1. (3.101)

Условие (3.101) можно записать раздельно для амплитуд

и фаз вектора; (/с>кр)- -

Л (ю

нр

) =

j WT(/со

кр

) I

= 1; (3.102)

Фх (°>кр)

Кр)

—°>кр

кр = —

« +

(

i03

)

где £ 0, 1, 2, 3, ... а

Из (3.102) можно найти сначала со

кр

, а затем из (3.103)

найти т

кр

, т. е.

—

^ (°>кр)+

№ +1)

+Ф

(«>кр)

2зт

i (ЗЮ4)

КР

©кр <0|ф Окр

Для систем автоматического управления с запаздыванием

основное значение имеет минимальное критическое время за-

паздывания (при i = 0), которое является в то же время и

граничным

. л t^ (^кр)

зт+Arctg —

зт+^(о>кр) _

(со

кр

) ф(сокр) (3.105)

Окр 0)

р 0)

где

<р

(со

кр

) = я + Arc tg

— запас устойчивости по фа-

зе.

Пример ЗЛО. Передаточная функция разомкнутой системы с за-

паздыванием

(s)=Ke-

/(l+sT).

Определить критическое время запаздывания т

кр

Частотная передаточная функция разомкнутой системы с запазды-

ванием

Следовательно, условие (3.102) в

данном случае

I (/*>кр) Г-1

[*/<1

+/о>кр Щ = 1.

Из последнего выражения находим критическую частоту:

кр "

Фазовый сдвиг на критической частоте

(сокр) = ~ Arctg со

Кр

Т = _ Arctg У/<

— 1.

-По (3.105) находим критическое время запаздывания:

зх—Arctg У К

— 1

зх

— Arctg У К

—

Тк

— Т •

кр

У к

— \

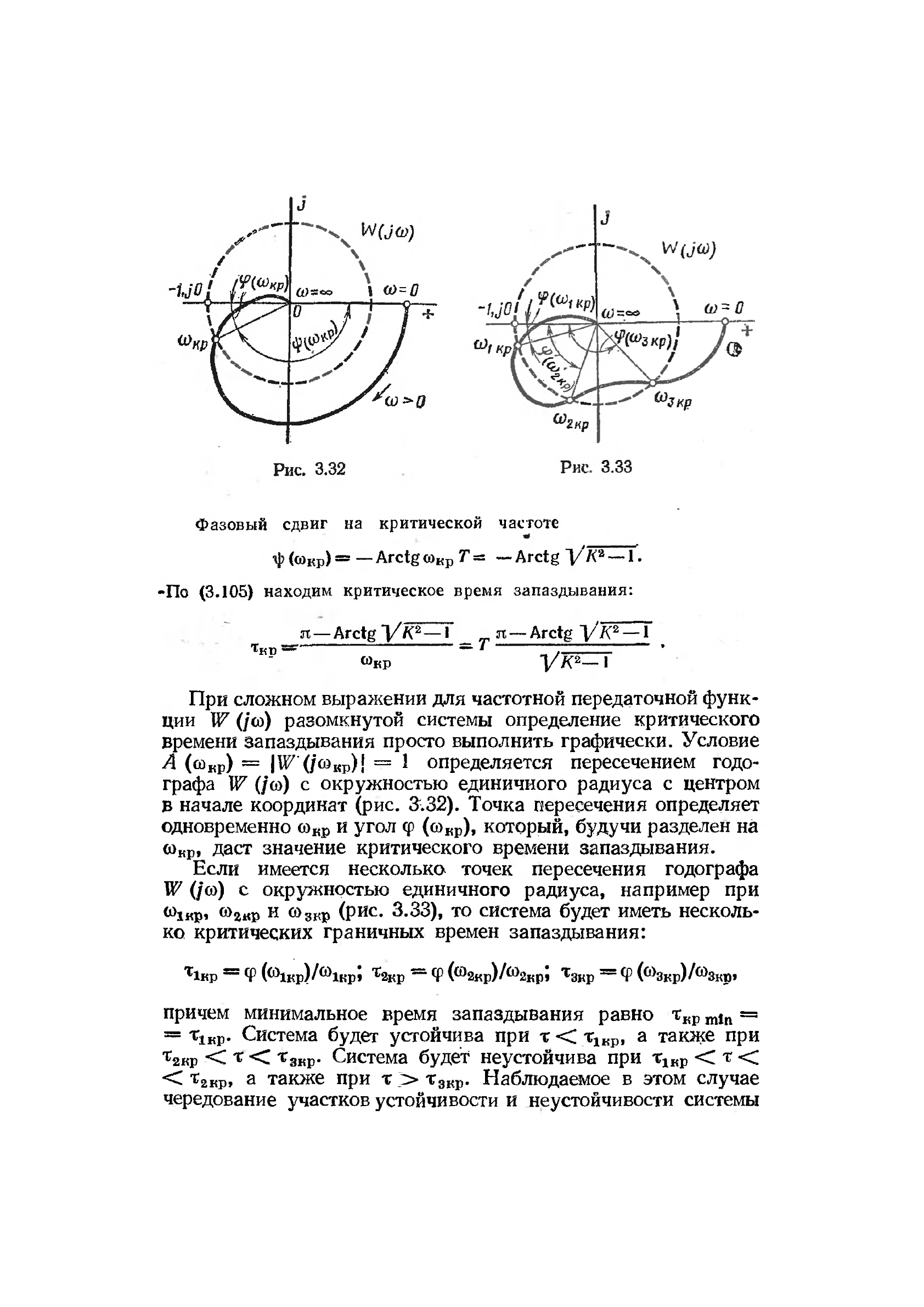
При сложном выражении для частотной передаточной функ-

ции W (/со) разомкнутой системы определение критического

времени запаздывания просто выполнить графически. Условие

А (со

кр

) = |W (/to

)j = 1 определяется пересечением годо-

графа W (/со) с окружностью единичного радиуса с центром

в начале координат (рис. 3v32). Точка пересечения определяет

одновременно со

кр

и угол

<р

(со

кр

), который, будучи разделен на

со

кр

, даст значение критического времени запаздывания.

Если имеется несколько точек пересечения годографа

W (/со) с окружностью единичного радиуса, например при

<*>1кр*

<*>2*Ф

°>зкр (рис. 3.33), то система будет иметь несколь-

ко критических граничных времен запаздывания:

1к

(оз

1кр

)/со

1кр

; т

2кр

(ш

2кр

)/со

2к]р

; т

3кр

<р

(о>

3кр

)/со

3кр

причем минимальное время запаздывания равно т

кр mln

= т

1кр

. Система будет устойчива при т< т

1кр

, а также при

2кр < т

<С

зкр

. Система будет неустойчива при т

1кр

< т <

^2кр> fl также при т ^зк

* Наблюдаемое в этом случае

чередование участков устойчивости и неустойчивости системы

при непрерывном изменении т (а также других параметров си-

стемы) является характерной особенностью многих систем с

постоянным за паздыван ием.

Обычно для повышения быстродействия и точности систе-

мы время запаздывания т стремятся уменьшить, поэтому кри-

терий устойчивости формулируется лишь для минимального

времени запаздывания.

Система автоматического управления будет устойчива,

если время запаздывания т меньше минимального критическо-

го времени запаздывания: т < т

кр m

Критическое время запаздывания легко определяют и в

том случае, когда для Исследования системы с запаздыванием

применяют логарифмические амплитудно-частотные (JTAX)

й фазочастотные (ЛФХ) характеристики. В этом случае окруж-

ность единичного радиуса представляют осью абцисс. JIAX

системы с запаздыванием совпадает с ЛАХ исходной системы

без запаздывания. Дополнительный фазовый сдвиг, который

надо учесть при построении ЛФХ системы с запаздыванием,

определяют из (3.100). Точки пересечения ЛАХ с осью абсцисс

определяют критические частоты со

аф

, а запасы по фазе

(с учетом кратности), отнесенные к соответствующем критиче-

ским частотам, определяют критические времена запаздывания

Ч'гкр-

Звенья с распределенными параметрами, описываемые

уравнениями в частных производных, имеют иногда передаточ-

ные функции вида

W(s) = K/V^ (3.106)

W7(s) =

/C/(1

(3.107)

W(s) = e-y

\ (3.108)

где К — коэффициент усиления звена.

Выражения (3.106) и (3.107) отличаются от передаточных

функций интегрирующего и инерционного звеньев (см. § 2.6)

только квадратным корнем. По аналогии с интегрирующими

и инерционными звеньями такие звенья называют полуинте-

грирующими и полуинерционными. Звенья, имеющие переда-

точные функции вида (3.106), (3.107), (3.108), называют ир-

рациональными звеньями. Выражение (3.108) не только ирра-

ционально, но и трансцендентно. С иррациональными звенья-

ми приходится встречаться, рассматривая различные диффу-

знойные и тепловые объекты, линии связи с потерями, с рас-

пределенными сопротивлениями и емкостями и т. п.

Устойчивость замкнутых систем автоматического управле

ния, содержащих иррациональные звенья, может быть иссле-

дована с помощью критерия устойчивости Найквиста. Форму-

лировка критерия устойчивости Найквиста в этом случае ана-

логична формулировке для обычных систем автоматического

управления, содержащих звенья с дробно-рациональными пере-

даточными функциями.

§ ЗЛО. Устойчивость нестационарных систем

Линейными системами с переменными параметрами или

нестационарными системами (см. § 2.9) называют системы,

процессы в которых описывается линейными дифференциаль-

ными уравнениями с переменными во времени коэффициен-

тами

[а

(t) р" + а

(0 р

•. •

On (Щ

х (0 -

«[&о (0 Р

+ h

(/)

+ ... +Ь

(01

g (0, (3.109)

где х (t) и g (t) — выходная и входная величины системы со-

ответственно; а

(t)

(t) — переменные коэффициенты, явля-

ющиеся известными функциями времени и задаваемые либо

графически, либо аналитически; р ~ d/dt — символ дифферен-

цирования.

Для нестационарных систем понятие устойчивости имеет

некотсррую специфику. Действительно, если предположить, что

входная величина системы g (t) = g

= const и к моменту

времени t

переходные процессы в системе закончились, т. е.

если принять р = d/dt = 0, то из (3.109) для t > t

имеем

= (3.110)

Из (3.110) видно, что в зависимости от характера измене-

ния коэффициентов а

(t) и b

(t) в нестационарной системе

даже при постоянной входной величине выходная величина мо-

жет изменяться неограниченно долго. Так как время работы

реальных систем ограничено, что установившегося значения

в нестационарной системе за время ее работы не наблюдается

и поэтому понятие асимптотической устойчивости (см. § 3.2)

практически теряет свой смысл.

Существуют точные методы исследования устойчивости не-

стационарных систем, но они довольно сложны и на практи-

ке .обычно пользуются приближенными методами.

Наиболее простым приближенным методом исследования

устойчивости нестационарных систем является метод замора-

живания коэффициентов. Он может применяться в тех слу-

чаях, когда нестационарная система работает в течение огра-

ниченного интервала времени Т

а коэффициенты уравнения

(3.109) за время протекания переходного процесса в системе

изменяются относительно мало. В соответствии с этим методом

для некоторого фиксированного значения времени t = t

определяют соответствующие ему значения а

) и b

)

коэффициентов дифференциального уравнения (3.109), заме-

няют исходную нестационарную систему некоторой фиктив-

ной стационарной системой и исследуют устойчивость послед-

ней, применяя один из рассмотренных выше критериев устой-

чивости. Если полученная таким образом стационарная си-

стема устойчива, то считают, что исследуемая нестационарная

система тоже устойчива в рассматриваемый момент времени.

Затем проводят аналогичное исследование устойчивости для

других фиксированных моментов времени, лежащих в интер-

вале 0 ^ t ^ Т

где Т — время работы системы.

—" Если во всем рабочем интервале времени Т условия устой-

чивости стационарной системы, получаемой методом замора-

живания коэффициентов, выполняются, то исходную нестаци-

онарную систему

на этом интервале считают устойчивой.

Следует заметить, что результаты, получаемые при иссле-

довании устойчивости нестационарных систем методом замора-

живания коэффициентов, не являются вполне достоверными,

поскольку сам этот метод не имеет какого-либо математиче-

ского обоснования. Степень достоверности будет тем выше,

чем меньше изменяются коэффициенты за время протекания

переходного процесса.

Эффективность рассматриваемого метода может зависеть от

правильного выбора фиксированных моментов времени, для

которых замораживаются коэффициенты.. Необходимо так

выбирать эти моменты, чтобы «охватить все возможные вариан-

ты значений коэффициентов, обратив особое внимание на

«опасные» точки, в которых происходит значительное изменение

коэффициента, смена его знака и т. п.

Пример 3.11. Система автоматического управления описывается

дифференциальным уравнением

loo Р*

+(О Р+

О»] * (t)

g (t), (3.11!)

где G

= 1 с

; a

= 4,2 с

; c

(t) — (72 — 0,l/)c; a

= 400; = 400.

Оценить приближенно устойчивость системы» если время работы

ее Г" 100 с.

Рассмотрим систему с замороженными коэффициентами при t = О

и t = Т ~ 100 с.

В этих случаях характеристическое уравнение, соответствующее

исходному дифференциальному уравнению (3.111), будет

0.1р

-ь 4,2р

+ 72р + 400 = 0; (3.112)

0,1р

+ 4,2р

+ 62 р + 400 = 0. (3.113)

Для (3.112) находим корни: р

= —10 с

-1

; ~ (—16 + /12) с-

. Сте-

пень устойчивости (см. § 4.5) ч = \р±\ =10 с-

. Время переходно-

го процесса t

< 3rj-i = 0,33 с. Для (3.113) корни р

= —25 с-

;

P2-S — (—8,8 ± /8,7) с-

. Степень устойчивости rj = 8,8 с-*. Время

переходного процесса t

^ З^р

= 0,34 с.

За время переходного процесса коэффициент а

(t) изменяется иа

величину Аа

« 0,1*0,34 = 0,034, что составляет приблизительно

0,05 %. Следовательно, система может рассматриваться как квазиста-

циоиариая. Оценка устойчивости может быть сделана методом'замора-

живания коэффициентов^ характеристического уравнения. Применяя

критерий устойчивости Гурвица, имеем а

(?) > а

. Подстанов-

ка числовых значений дает 4,2 (72 — 0,10 >40. Последнее неравенст-

во выполняется в диапазоне времени 0 ^ t ^ Т. Следовательно, ис-

ходная нестационарная система устойчива.

В общем случае, когда коэффициенты уравнения (3.109)

изменяются значительно, при исследовании устойчивости не-

стационарных систем пользуются понятием технической устой-

чивости, или устойчивости на конечном интервале времени.

Систему считают технически устойчивой (устойчивой на

данном интервале времени работы системы Т), если вы-

ходная величина х (0 не превосходит некоторой заданной

величины х

поп

при O^J^LT.

Допустимое значение вели-

чины Хдоц выбирается в

каждом конкретном случае

из технических соображе-

ний.

На рис. 3.34 показа-

ны возможные графики

изменения х (t) для неста-

ционарны х систем. Кривые

/и 2 соответствуют тех-

нически устойчивой системе, а кривые 3 и 4 — технически не-

устойчивой системе. Из рис. 3.34 видно, что система может

быть одновременно устойчива технически и неустойчива

асимптотически (кривая 1) и, наоборот, неустойчива техниче-

ски и устойчива асимптотически (кривая 3). Так как в неста-

ционарной системе изменение х (/) зависит от момента подачи

входного сигнала g (t), то на техническую устойчивость будут

оказывать влияние и начальные условия, и характер входно-

го сигнала.

В настоящее время не существует достаточно простых и

достаточно общих критериев технической устойчивости. По

существу, единственный способ проверки устойчивости неста-

ционарных систем заключается в нахождении кривой выход-

ной величины х (0 при заданном входном воздействии g (t)

(внешнем возмущении). Определение х (t) производят обычно

либо с помощью различных приближенных аналитических ме-

тодов, либо методами математического моделирования на ана-

логовых или цифровых вычислительных машинах.