Воронов А.А. Теория автоматического управления. Часть первая

Подождите немного. Документ загружается.

§ 4.5. Корневые методы оценки качества

регулирования

Известно, что характер переходного процесса в системе

определяют по ее реакции на единичное ступенчатое воздей-

ствие. Переходная характеристика h (t) системы может быть

вычислена с помощью обратного преобразования Лапласа

(по формулам разложения Хевисайда):

A(/)= L-I|-L w

(s)J

Pis)

sD (s)

Если D (s) не имеет кратных корней, то

h(t)=

£121.4-у

D (0)

P(Si)

Si t

D' (

)

(4.15)

где

— корни характеристического полинома замкнутой си-

стемы D (s) = 0; D' (sj) — dD (s)/dk|

s=s

. — первая произ-

водная характеристического полинома D (s) по s при s = s

Из (4.15) видно, что на характер переходного процесса

влияют и числитель и знаменатель передаточной функции зам-

кнутой системы W

(s). Если числитель W

(s) не имеет ну-

лей, т. е. представляет собой постоянную величину, то харак-

тер переходных процессов можно оценить по ее полюсам, т. е.

корням характеристического уравнения замкнутой САУ

D (s) = 0.

Для приближенной оценки качества переходного процесса

в системе нужно на плоскости корней s выделить область, в

которой располагаются корни ее харак-

теристического уравнения. Чаще всего

эту область представляют трапецией

(рис. 4.7). Корни характеристического

уравнения располагаются внутри этой

трапеции ABCD, на ее сторонах и ос-

нованиях хотя бы по одному корню, а

вне ее—ни одного. Для выделения этой

области на плоскости корней вычисляют

параметры: степень устойчивости г|, ко-

лебательность {г и значение £ веществен-

ной части максимально удаленного кор-

ня от мнимой оси. Рис. 4.7

0 Re

Понятие степени устойчивости rj введено Я. 3. Цыпкиным

и П. В. Бромбергом. Степенью

устойчивости

rj называют рас-

стояние от мнимой оси до ближайшего корня или ближайшей

пары сопряженных комплексных корней. Степень устойчиво-

сти

г]

определяет ближайшее к мнимой оси основание трапеции

AD (рис. 4.7).

Пусть общее решение дифференциального уравнения си-

стемы

x(t)= V C

* \ (4.16)

где — корни характеристического уравнения D (s) — 0.

Составляющая этого решения, определяемая степенью ус-

тойчивости, запишется в виде

(*)=C

e-n* (4.17)

для случая вещественных корней или

Хц

(0 - С

sin (4.18)

для случая, когда среди корней есть пара комплексно-сопря-

женных.

В большинстве случаев переходный процесс можно счи-

тать закончившимся тогда, когда затухнет составляющая пере-

ходного процесса, определяемая степенью устойчивости^ т. е.

порядок величины времени затухания процесса можно грубо

оценить по наиболее медленно затухающей составляющей

хц (/) [см. (4.17), (4.18)1. В случае, когда ближайшим к мнимой

оси является вещественный корень, из (4.17) можно получить

следующую зависимость: ж ~ In . Если принять, на-

пример, А = 0,05, то время переходного процесса t

= — X

X In ^ 3/rj. В том случае, когда ближайшей к мнимой

оси является пара комплексных корней, из (4.18) можно найти

I 1

верхнюю границу времени переходного процесса: t

1п .

Можно поставить две задачи:

1. По заданным параметрам- системы — коэффициентам

D (s) — определить степень устойчивости системы (задача ана-

лиза степени устойчивости).

2. По заданной степени устойчивости определить значе-

ние варьируемых параметров системы (задача синтеза САУ

по заданной степени устойчивости).

Воспользуемся методом, изложенным в [12]. Предлагает-

ся сместить мнимую ось влево на величину г), тогда один ко-

рень окажется на мнимой оси, а система — на границе устой-

чивости. Это соответствует обращению в нуль старшего опре-

делителя Гурвица: Д

= а

-А

= 0. Это условие дает урав-

нение, по которому, задаваясь коэффициентами, можно опре-

делить или решить обратную задачу.

Пусть характеристическое уравнение системы

D(s) —а

s" +... + +

Введем новую перемецную z = s + irj. Подставив значение

s = z — л в уравнение D (s) = 0, получим новое смещенное

уравнение:

# + Л

+ ... + А

z + -0, (4.19)

где

. (4.20)

(n-i)l L dsn-*

Если в смещенном уравнении окажется А

= 0, то ближай-

шим к мнимой оси окажется нулевой корень, а если А

Ф 0,

то пара сопряженных комплексных корней.

Условие границы устойчивости для системы, описанной

уравнением (4.19), по критерию Гурвица = 0 при соблю-

дении всех остальных условий устойчивости Гурвица.

Колебательностью системы называют тангенс угла, об-

разованного отрицательной вещественной полуосью и лучом из

начала координат к корию, у которого отношение мнимой ча-

сти к действительной максимально (рис. 4.7):

Ц = tg

= (p/aU, (4.21)

где Р — значение мнимой части корней D (s); a—действи-

тельная часть.

При известных параметрах системы можно определять зна-

чение колебательности JLI (задача анализа колебательности)

или решать обратную задачу — задачу синтеза САУ по задан-

ной колебательности. Для этого в характеристическое урав-

нение системы вводится замена s = jze~

, равноценная по-

вороту мнимой оси на угол (я/2 — фдг), при этом пара сопря-

женных комплексных корней окажется на мнимой оеи, а фик-

тивная система — на границе устойчивости. Колебательность

|л является оценкой переходного процесса сверху, при уве-

личении fi возрастает число колебаний п за время регулирова-

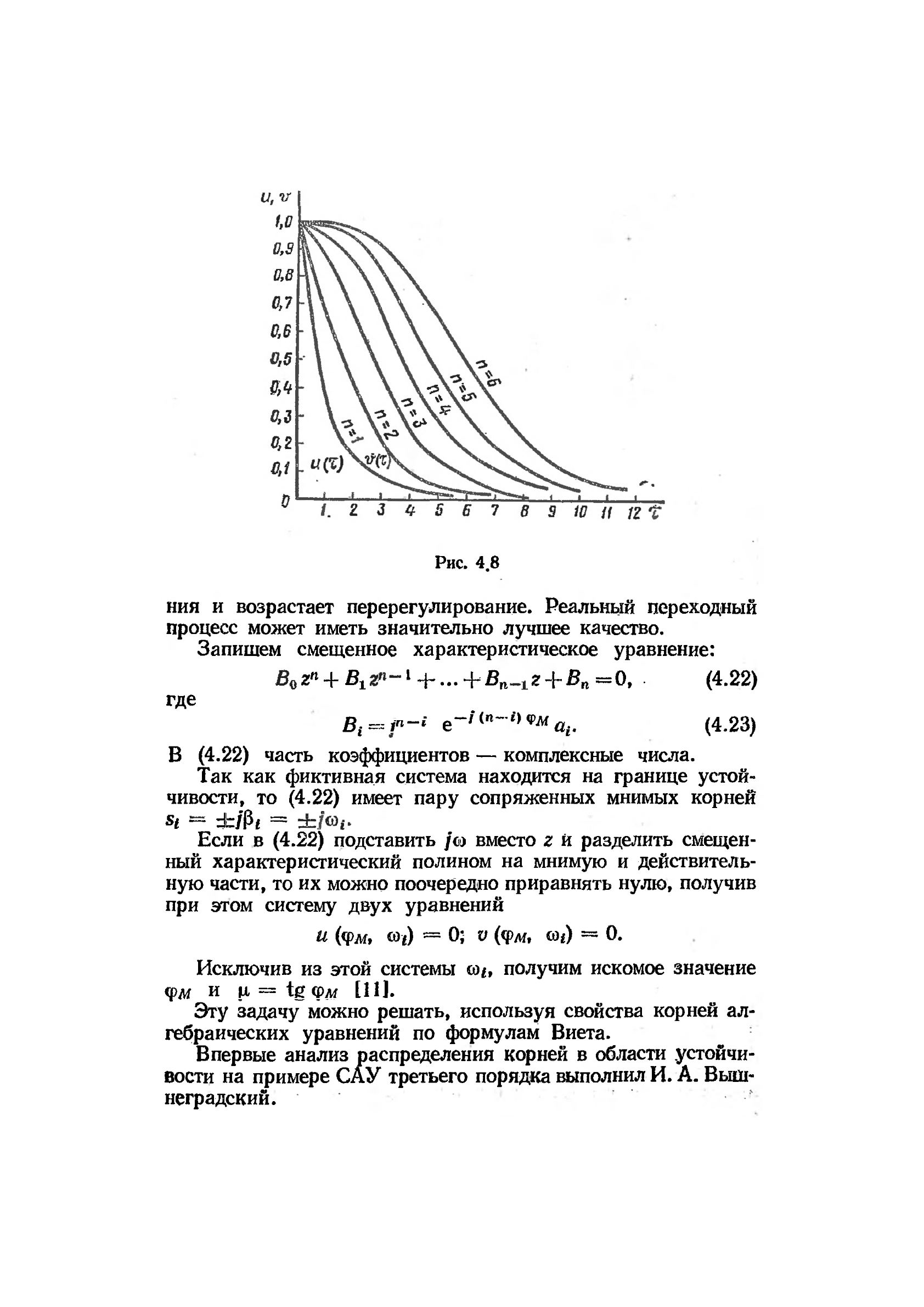
Рис. 4.8

ния и возрастает перерегулирование. Реальный переходный

процесс может иметь значительно лучшее качество.

Запишем смещенное характеристическое уравнение:

z« + В

+... + В

z + B

в0, (4.22)

где

(

= e

W(B

ФЛ

(4.23)

В (4.22) часть коэффициентов — комплексные числа.

Так как фиктивная система находится на границе устой-

чивости, то (4.22) имеет пару сопряженных мнимых корней

St — db/Pi =

Если в (4.22) подставить /со вместо г й разделить смещен-

ный характеристический полином на мнимую и действитель-

ную части, то их можно поочередно приравнять нулю, получив

при этом систему двух уравнений

и (фм, щ) 0; v (фм, «О = 0.

Исключив из этой системы со*, получим искомое значение

фА* И [11].

Эту задачу можно решать, используя свойства корней ал-

гебраических уравнений по формулам Виета.

Впервые анализ распределения корней в области устойчи-

вости на примере САУ третьего порядка выполнил И. А. Выш-

неградский.

Оценка прямых показателей качества переходного процес-

са — времени регулирования и перерегулирования а

(см. § 4.3) — по известным tj, 5 и fi для любого распределения

корней и любых начальных условий пока не найдена. Но для

определенных классов распределения корней и начальных

условий можно построить две кривые: мажоранту и миноран-

ту, которые ограничивают кривую переходного процесса свер-

ху и снизу:

и(0 »(0. (4.24)

где и {t) — миноранта, a v (t) — мажоранта.

Методы построения мажорант и минорант разработаны

С. А. Чаплыгиным, Н. Н. Лузиным, А. А. Фельдбаумом [111

и уточнены А. М. Рубинчиком [8].

Приведем некоторые формулы для расчета мажорант и

минорант без доказательства. Для случая вещественных кор-

ней и нулевых начальных условий х (0) = 0, х' (0) = ... =

г=г дЧ"-

) (0) — 0 мажоранта и миноранта описываются соот-

ветственно уравнениями

,/г—1 i

v(t) 1+4* + ...+

С"

—1)1

(4.25)

(4.26)

и, v

Перерегулирование для этого класса корней отсутствует.

На рис. 4.8 показаны кривые и

(%)

и v (т) для разных степеней

уравнения, причем т = v\t — относительное время. Чем выше

/2, тем грубее оценка. Если

учесть величину то можно

сблизить миноранту и ма-

жоранту [2, 11).

Для систем, имеющих

среди корней пару комплекс-

но-сопряженных, при тех же

начальных условиях мажо-

ранта описывается уравнени-

ем (4.25), а миноранта

и (t) - — v (/). (4.27)

При этом перерегулирование

(4.28)

Если х (0)=x

то

что проиллюстрировано на

рис. 4.9.

бщах

Рис. 4.9

Используя мажоранту и миноранту, можно оценить вре-

мя регулирования переходного процесса:

где t

— время регулирования по миноранте; t

— время ре-

гулирования по мажоранте.

§ 4.6, Корневые годографы

Траектории, описываемые на комплексной плоскости кор-

нями характеристического уравнения замкнутой системы при

плавном изменении одного из ее параметров от 0 до оо, назы-

вают корневым годографом. Располагая корневым годографом,

можно выбрать необходимое значение варьируемого парамет-

ра, соответствующее наиболее выгодному расположению кор-

ней с точки зрения требований к качеству конкретной систе-

мы. В СССР основополагающими работами в этом направле-

нии были работы К. Ф. Теодорчика, развитые Г. А. Бендрико-

вым и С. П. Стрелковым в 1948—1949 гг., в США — работы

В. Ивенса в 1950 г.

Используя метод корневого годографа, можно решать сле-

дующие задачи [9J: построение годографов полюсов передаточ-

ной функции замкнутой системы при изменении одного из ее

параметров; оценки влияния параметров системы, появляю-

щихся при ее усложнении; качественной и количественной

оценки реакции системы на типовой сигнал при изменении зна-

чения параметра системы; синтеза корректирующих элемен-

тов системы.

Для непрерывных линейных систем существует несколько

методов построения корневых годографов, в частности ме-

тода Ивенса, Теодорчика—Бендрикова и Удермана. Наибо-

лее трудоемким является метод Ивенса. Используя этот ме-

тод, можно оценить несколько вариантов с точностью 3—5 %,

что удобно на первом этапе проектирования. Метод Теодор-

чика—Бендрикова позволяет проводить более детальные рас-

четы с использованием ЭВМ.

Рассмотрим метод Ивенса. Передаточная функция замкну-

той системы (рис. 4.10)

(s) = W

(s)/[\ + W

(s) W

(s) 1, (4.29)

где W

(s) W

(s) - № (s) (4.30)

— передаточная функция разомкнутой системы.

0 Re

Рис. 4.10

Рис. 4.11

ИЛИ

Характеристическое уравнение замкнутой системы

D(s) = I + W

(s) Г

(s) = 0 (4.31)

W (s) -

— 1.

(4.32)

Надо отметить, что излагаемый метод наиболее пригоден

для выбора общего коэффициента k передаточной функции ра-

зомкнутой системы . W (s), которая содержит его как мно-

житель.

Уравнение (4.32) можно записать в виде системы уравне-

ний относительно модулей и фаз:

(4.33)

(4.34)

\W (8)\ - \W

(s) W

is) 1

- 1;

arg W (s) ±(2i + 1) я,

где i — 0, 1, 2, ...

Уравнение корневых годографов (4.34) является основой

для их построения.

Пусть известны нули и полюсы передаточной функции

разомкнутой системы: s

..., s

— полюсы,"^, s

, s

—

нули. Тогда передаточная функция разомкнутой системы

W (

Jg=l>k-q) ... (s~7

)

{s—s

) (s—s

) ... (s— Sn)

(4.35)

где a — множитель, появляющийся при разложении числи-

теля и знаменателя W (s) на множители; k — общий коэффи-.

циент усиления; т ^ л.

Сомножители (двучлены) числителя (s — s

) и знаменате-

ля (s — Si) функции (4.35) на плоскости корней изображают-

ся векторами (s — sj) и (s — которые образуют с вещест-

венной осью углы 6,-(6

) (рис. 4.11). Тогда аргумент W (s)

можно записать как разность аргументов числителя и знаме-

т п

нателя arg W (s) = £ 0/ — 2 6,- и уравнение (4.34) при-

мет вид

m я

Е 2

±(2v-f 1)л, (4.36)

где v = О, I, 2, ...

Уравнение (4.33) удобнее представить как

\W (s)| = akl = 1.

или

причем

к « 1/(я/), (4.37)

Ш I п

I = П h / п /,, (4.38)

/ — 1

I г I

где — длина соответствующих векторов (s — s^)» / — I, ...,

..., m; l

— длина векторов (s — s

), e = 1, ...» п.

Корневые годографы строят по (4.36), куда k не входит.

Для уже найденных корней по (4.37) определяют к. В. Ивен-

сом предложено специальное устройство «Spirub для ускоре-

ния построения корневых годографов. Оно состоит из проз-

рачного транспортира для сложения углов (0) и логарифмиче-

ской спирали для перемножения длин векторов (/), по кото-

рым определяют величину к. Описание этого устройства при-

ведено в {2] и работах В. Ивенса.

Построение корневых годографов требует знания их

свойств, которые приведем ниже без доказательств.

!. Комплексные части корневых годографов попарно со-

пряжены, и ветви годографа симметричны относительно ве-

щественной оси.

2. Число ветвей корневого годографа равно порядку урав-

нения D (s)

—

0, т. е. числу полюсов передаточной функции

замкнутой системы W

(s).

3. Ветви корневого годографа начинаются при к = О

в полюсах передаточной функции разомкнутой системы W (s).

4. При к оо т ветвей корневого годографа стремятся

к т нулям передаточной функции разомкнутой системы, а

остальные п — т ветвей уходят в бесконечность.

5. п — т ветвей корневого годографа, уходящие в беско-

нечность, имеют асимптоты, число которых равно разности

Рис. 4.12

порядков числителя и знаменателя передаточной функции

разомкнутой системы W (s), т. е. п — т. Асимптоты выходят

из одной точки на вещественной отрицательной полуоси с аб-

сциссой

/ « /и - \ /

о„ = f 2

®<

- 2 ^) / (" -'") (4-

)

под углами

е„ = (2i + 1) п/(п — т), (4.40)

где i — 0, I, 2, ..., п — т — 1.

6. Точки пересечения корневого годографа с мнимой

осью могут быть найдены с использованием одного из крите-

риев устойчивости. Если п ^ то эти расчеты не вызовут

трудностей, а для систем более высокого порядка эта часть

построения годографа наиболее трудоемка. В этом случае

можно рекомендовать алгоритм Рауса, чрезвычайно удобный

для реализации на ЦВМ, или метод проб по уравнению фаз

(4.36).

7. Точки на действительной оси, из которых одна ветвь

корневого годографа уходит в верхнюю полуплоскость, а со-

пряженная ей ветвь — в нижнюю или, наоборот, приходят в

эти кратные точки (кратные корни на действительной оси),

можно найти из условия нулевого приращения суммы арг\

ментов в (4.36) при переходе от этой точки к близкой ей, ж-

лежащей на действительной оси. При этом нужно учитывав

знаки приращения углов ДО.

Проиллюстрируем примером определение точек пересе

чения с действительной осью. На рис. 4.12 показано располо-

жение полюсов передаточной функции разомкнутой системы,

= —

— двукратный нуль. Определим величину а. При уве-

личении k на М двукратный нуль превратится в два комплек-

сно-сопряженных: s

и s

. В уравнении (4.36) ввиду малости

Д0 заменим их тангенсами, тогда получим

со/а — o)/(|s

| — а) — co/(|s

| — а) — 0, а > 0.

Сокращая со, определим величину а.

8. Ветви корневого годографа, совпадающие с отрезками

действительной оси, располагаются в тех ее частях, справа от

которых находится нечетное число действительных нулей и

полюсов разомкнутой системы. Это свойство является следст-

вием уравнения (4.36).

9. При (п — т) > 2 часть ветвей корневого годографа от-

клоняется влево от мнимой оси, а другие — вправо. В [9]

показано, что при оценке переходных процессов можно учиты-

вать лишь те ветви годографа, которые отклоняются вправо.

Те из них, которые располагаются ближе к мнимой оси, назы-

ваются доминирующими. Иначе говоря, система n-го порядка

в динамике будет вести себя как эквивалентная система более

низкого порядка, нули и полюсы которой совпадают с группой

нулей и полюсов, наиболее близких к мнимой оси и началу

координат плоскости s.

10. Углы выхода из комплексного полюса и углы входа в

комплексный нуль определяют из уравнения фаз (4.36), запи-

санного для этого полюса или нуля, т. е.

- ±(2v + 1) 180° — 26. (4.41)

Рассмотрим пример построения корневого годографа с ис-

пользованием перечисленных выше свойств.

Пример 4.2. Пусть известна передаточная функция разомкнутой

системы

W (s) [k (s + 3)1 /{s (s -f 4) (s

+ 2s + 2)1

Характеристическое уравнение замкнутой системы

D (s) = s

+ 6s

-f- 10s

+ (8 + k) s + Zk — 0.

Передаточная функция разомкнутой системы имеет нули: s

® —3

и полюсы; s

=0, s

~ —4, s

3t4

— —

± /1-

Расположение нулей и полюсов на плоскости s показано на

рис. 4.13. Число ветвей корневого годографа равно 4 (свойство 2). Со-

гласно этому свойству, при к = 0 ветви начинаются в полюсах s

3»

и П

(свойство 4) одна ветвь стремится из полюса

0 в нуль^! — —3, а из полюса s

= —4 стремится в бесконечность

по действительной оси (рис. 4.14).