Воронов А.А. Теория автоматического управления. Часть первая
Подождите немного. Документ загружается.


s*
А
От
У
л
0
'
s
z
S, -2 -1
s,
1
0 1 2 Re
sj
—
-1J
sj
-1J
-ч -j -г -1
V
От
U
О Re
-и
Рис. 4.13
Рис. 4.14
Определим число асимптот: п — от = 4 — 1=3 (свойство 5).
Определим координату пересечения асимптоты с действительной осью,
{п — т) =
=
[0
—4—
1
— 1—(— 3)]/(4— 1)~ —
1
и углы асимптот:
• (2
г
- I) 1807(и — от),
е
а
где i=0, 1, 2; . 6
аг
= 18073 ~ 60°; 6
в8
= (2 -f !) 18073 «т !80°;
©аз ^ (4-Ы) 18073 = 300° = —60° (рис. 4.15).
Определим точки пересечения с мнимой осью (свойство 6). По
критерию Гурвица, для уравнения
D (s) = a
0
s
4
•+ ^s
3
4- a
2
s
2
-f a,s -f я. = s
4
-f 6s
3
+
!
0s
2
+ k) s + 3k — 0,
уравнение границы устойчивости
Л
3
= aia
2
a
3
—
a
0
a§
—
0.
Отсюда k
r
jy = 6, а граничная частота
Щ —
a
jai ~ V
14
/
6
— ±1,53 (рис.
4.16).
Определим углы выхода годографа
из полюсов s
3
и s
4
(свойство 10):
(8 +
Ч "3 -2 -
-
(Qi
+
%
+ в
3
+е
4
) - 180°.
Углы 6|_, в^ 0
2
, 6
3
, в
4
указаны на
рис. 4.13: в
Л
- 26,5°; Q
r
= 135°; 6
2
=
= 18,2°; в
4
- 90°; в
3
- —(180° + +
4
в
а + в
4
) - в
х
- — 36,7°.
am
/
V ,
/
+60°
%
-ЛА -ЛА
V -
Яе
Рис. 4.15

Чтобы определить при k — £
гр
= 6 полюсы на вещественной от-
рицательной полуоси (чисто мнимые уже определены: s
3f4
=•
= dzjto о — zfcl ,53/), воспользуемся свойством корней (свойство
Виета).
п
1. П — а
п
/а
0
; % % $4™3£
ГР
/1.
i— 1
Так как s
3
s
4
=cog, то $! s
2
= 3fe
r
p/cog.
п
2
- 2 sj-f S2+S3+S4— — 6.
x=
1
Так как s
3
+ s
4
= 0, то + s
2
— —6.
Решаем систему уравнений:
s
2
—3»6/l ,53
2
; I
$1+Sg
= /
$!= —1,8; s
2
= —4,2.
Если необходимо повысить точность расчетов, то нужно использо-
вать уравнение (4.36).
Рассмотрим еще один метод построения корневых годогра-
фов, предложенный Э. Г. Удерманом [6, 9]. В предлагаемом
методе для построения корневого годографа используется кри-
вая D-разбиения в плоскости варьируемого параметра с помо-
щью годографа затухания.
Выделим в характеристическом уравнении замкнутой си-
стемы D (s) варьируемый параметр А. Тогда характеристиче-
ское уравнение S (s) +
+ AR (s) - 0.
Уравнение кривой
D-разбиения в плоско-
сти параметра А
А = -S (/со)/* (/со).
(4.42)
Уравнение (4.42) поз-
воляет в комплексной
плоскости А выделить
область устойчивости
системы, т. е. ту область,
где корни уравнения
\-1,53j=-ja)
c
D (5) = о имеют отрица-
тельную вещественную
Рис. 4.16 часть.
От
S
2
S
f
(К
гг
6)
«ф • I •••'
Д^рдфи
(>VS)-4 -J ~Z -
53'j
-Jo)
0
Re

Ct Ei <
w
*)
1(0,)
(Щ)
Щ
Рис. 4.17
Удерманом введено
пяА
понятие годографа за-
тухания [9].
Годографы затуха-
ния — линии постоян-
ной частоты со = const
и переменного затуха- (<о=о)
кия а = var в плоско-
сти варьируемого пара-
метра Л, т. е. годографы
затухания — это отобра-
жения линий, перпен-
дикулярных мнимой оси
в плоскости корней s,
а так как кривая D-разбиения является конформным ото-
бражением мнимой оси на плоскости параметра 4» то годо-
графы затухания ортогональны кривой D-разбиения (рис. 4.17).
Л
1гр
,
Л
2гр
— это отрезок устойчивости.
Из точек С
х
, С
2
и С
3
(на кривой D-разбиения) проведены
три годографа затухания до пересечения с отрезком устойчиво-
сти в точках D
l9
D
2
И
D
3
. В точке В
г
характеристическое урав-
нение имеет в числе прочих пару комплексно-сопряженных
корней Si = —
a
i dr /со 1 при А — А
г
. В точке D
2
при А =
= Л
2
корни Sj
f
2 = —
а
2 ± /со2. в точке D
3
при Л — Л
3
кор-
ни s
lf2
— —а
3
гЬ /со3. Таким образом, можно построить до-
минирующие ветви корневого годографа при изменении зна-
чения параметра Л.
В [9] показано, что для определения величины а в точках
пересечения годографа затухания с отрезком устойчивости
нужно оценить отрезок кривой D-разбиения С
1
Е
1
~ C
1
D
1
в
единицах частоты. Тогда
сс±
u)j — со \. Аналогично посту-
пают для точек D
2S
D
3
И Т. Д.
Для построения корневого годографа нужно в (4.42) за-
менить s на (—а + /со):
Л (—а + /со) - —S (—а + /со)//? (—а + /со). (4.43)
Используя разложение в ряд Тейлора для полиномов
S (—а + /со) и (—а + /со), (4.43) можно представить [9J
как
Л(—а +
/со)
= I В(а)—— В"(а)4
I . 2!
4!
Я<4)
(а)+ ...] +

+/<о [_ В* (а) + ^L Bi3) (а) ] j {|с (а) -
С"
(а) +
С<4>
(а)- ... ] +
/со
[ —С' (а) +
С"
(а) - ... ] (4.44)
где В (а) — S (—а); С (а) - # (—а); Б' (а) = (a)/da;
С
(a)
= dC(a)/da] R"
(а)
- d
2
В (a)/da
2
;
С" (a)
=
d
%
C
(а) / da
2
.
Чтобы определить действительные корни характеристиче-
ского уравнения D (s) — 0, нужно использовать (4.44) при
€0 — 0.
Пример 4.3. Дана передаточная функция разомкнутой системы
W (s) - k/[(\ + sTi) (1 + sT
2
) (1 + sT
3
)h
где T
t
= 0,1 с; Г
2
= 0,2 с; Т
3
= 0,3 с.
Варьируемый параметр в данном случае k. Характеристическое
уравнение замкнутой системы
D (s) = (1 -Ь sT
x
) (1 + sT
2
) (1 + sT
3
) + k = 0.
Уравнение кривой D-разбиения (рис. 4.18) в плоскости k
ь = -о + i<»Ti) (1 + /^r
2
) (1 + /соГ
3
).
В соответствии с (4.44) запишем выражение для k (—а + /со):
k l—cc-hjo) = [/?
+
- — [a
0
s
3
-f + + =
= (a) + В» (a)
J
+
/со
J
- В' (a)-j-<~ B<
3
>
(a)
j
f
где а
0
= ЛТ
,
2
Г
3
= 0,008; = (Г
х
Г
2
+ Г
2
F
3
-f 7\ Г
3
) = 0,14;
Й
2
==7\ + Г
2
+ Г
3
=:0,7; I, В (а) - £ а) =я
0
«1 а
2
—«з»'
В' (а) = Зя
0
а
2
— 2а
г
а +
а
2
;
В" (а) = 6а
0
a —2^; B
ff
'(a)=-6a.
Тогда
k (
—
a + /co)
(О
2
По
a
3
—«J a
2
-j-a
2
a—+ —^ (6% ос—2%) | +
Г
+
/co
I —3a
0
а
2
+ 2а
х
a—~а
2
+ 6a
0
2
- [0,008a
3
—0,14ct
2
+ 0,7a ~
6
_
1
4.
(02
(0 j024a
_о
e
14)
]
+
fa
[
__0,024a
2
+ 0,28a— 0,7 +0,008co
2
l.
Если принять a = 0, то получим уравнение кривой D-разбиения
Проведем из точки C
lt
соответствующей частоте со = 4, годограф
затухания до пересечения с отрезком устойчивости (—1 ~г 11,25).
В точке D
t
определим значение k — 1,8; а
х
= 5,5 — 4 = 1,5.
Аналогично, для годографа затухания из точки С
2
k
2
~ 7,5;
а
2
= 8,6 — 8 — 0,6 и т. д. (рис. 4.18, а).
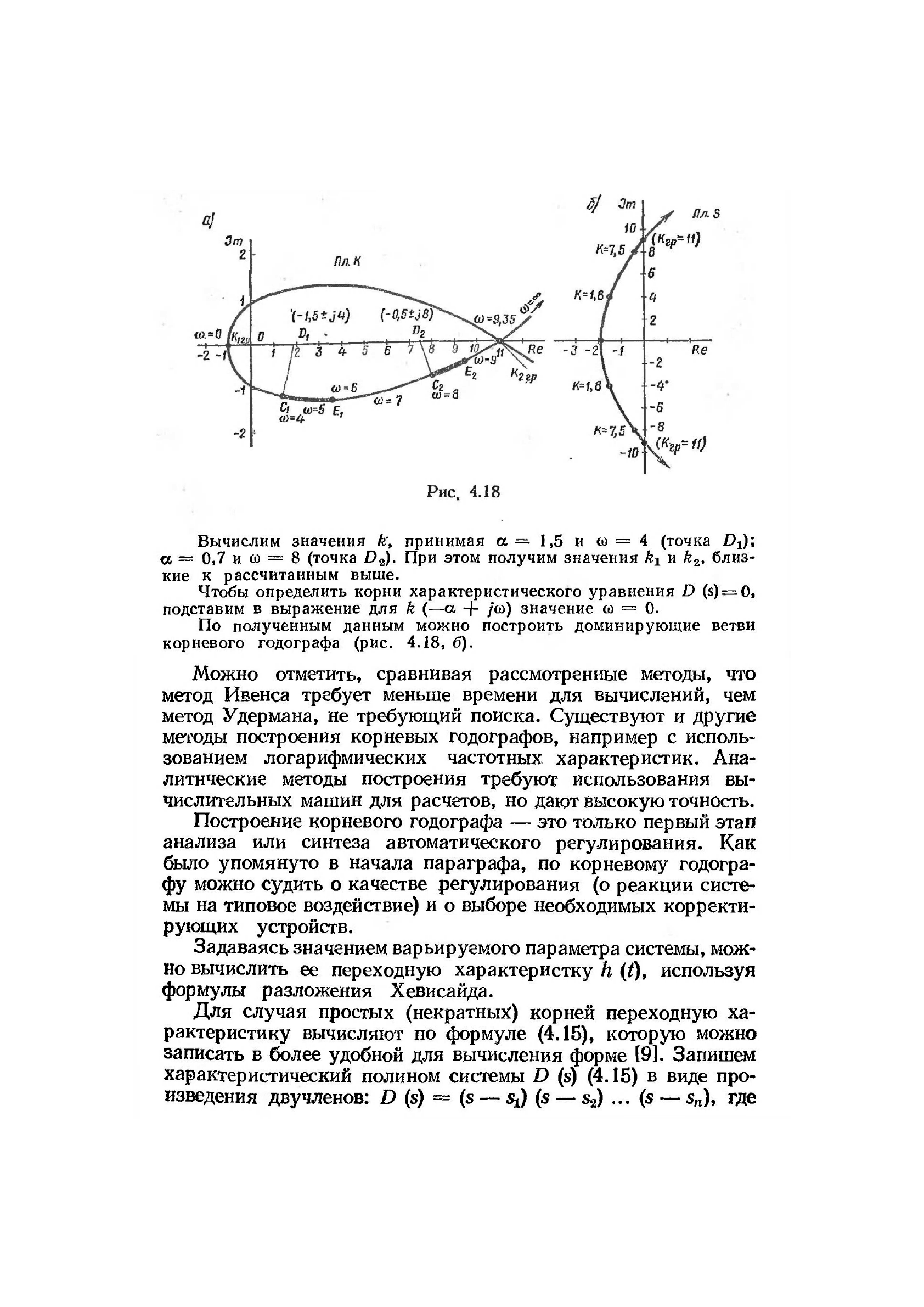
Вычислим значения k\ принимая а — 1,5 и со = 4 (точка DJ;
а = 0,7 и о = 8 (точка D
2
). При этом получим значения к
±
и к
г%
близ-
кие к рассчитанным выше.
Чтобы определить корни характеристического уравнения D (s)~0,
подставим в выражение для к (—а + /со) значение со = 0.
По полученным данным можно построить доминирующие ветви
корневого годографа (рис. 4.18, б),
Можно отметить, сравнивая рассмотренные методы, что
метод Ивенса требует меньше времени для вычислений, чем
метод Удермана, не требующий поиска. Существуют и другие
методы построения корневых годографов, например с исполь-
зованием логарифмических частотных характеристик. Ана-
литические методы построения требуют использования вы-
числительных машин для расчетов, но дают высокую точность.
Построение корневого годографа — это только первый этап
анализа или синтеза автоматического регулирования. Как
было упомянуто в начала параграфа, по корневому годогра-
фу можно судить о качестве регулирования (о реакции систе-
мы на типовое воздействие) и о выборе необходимых корректи-
рующих устройств.
Задаваясь значением варьируемого параметра системы, мож-
но вычислить ее переходную характеристку h (t), используя
формулы разложения Хевисайда.
Для случая простых (некратных:) корней переходную ха-
рактеристику вычисляют по формуле (4.15), которую можно
записать в более удобной для вычисления форме [9]. Запишем
характеристический полином системы D (s) (4.15) в виде про-
изведения двучленов: D (s) = (s — sj (s — s
2
) ... (s — s
n
), где

Sit s
2
t S
n
— его корни. Определим производную D' (s) —
— dD (s)/ds
y
принимая для простоты n = 3:
AD (s)/ds = (s — s
2
) (s — s
3
) + (s — sj) (s — s
3
) + (s — Sj) X
X (s — s
2
).
Подставляя в это выражение s = s
lt
обратим в нуль все сла-
гаемые, кроме первого, при s
—
s
2
— все, кроме второго,
при s — s
3
— все, кроме третьего. Таким образом, значение
производной £>' (s) при s = S| будет равно произведению
п — 1 сомножителей
& fa) - П (si-s
h
).
Заменяя в (4.15) D' (s
f
) полученным выражением, можно на-
писать следующую формулу для вычисления характеристики:
ii^M+y
PW)eV
. (4.45)
D(0) ^ ft п *
кф i
Этим выражением удобно пользоваться, располагая по-
строенными корневыми годографами, определяя значения
длин и аргументов векторов fa — s
k
) по чертежу годографа.
Подробнее с упомянутыми вопросами можно ознакомиться
в [91
§ 4.7. Интегральные оценки качества
переходных процессов
Интегральные оценки качества являются интегралами по
времени от некоторых функций переходного процесса свобод-
ной составляющей выходной величины х
св
(t) или ошибки
е
св
(<)
#
Цель использования таких критериев состоит в том,
чтобы получить общую оценку быстродействия и отклонения
регулируемой величины от установившегося значения. Широко
используются линейные и квадратичные интегральные оценки.
Линейные оценки вычисляются по формуле
оо
J
0
= je~
at
t
n
е
св
. (4.46)
0 •
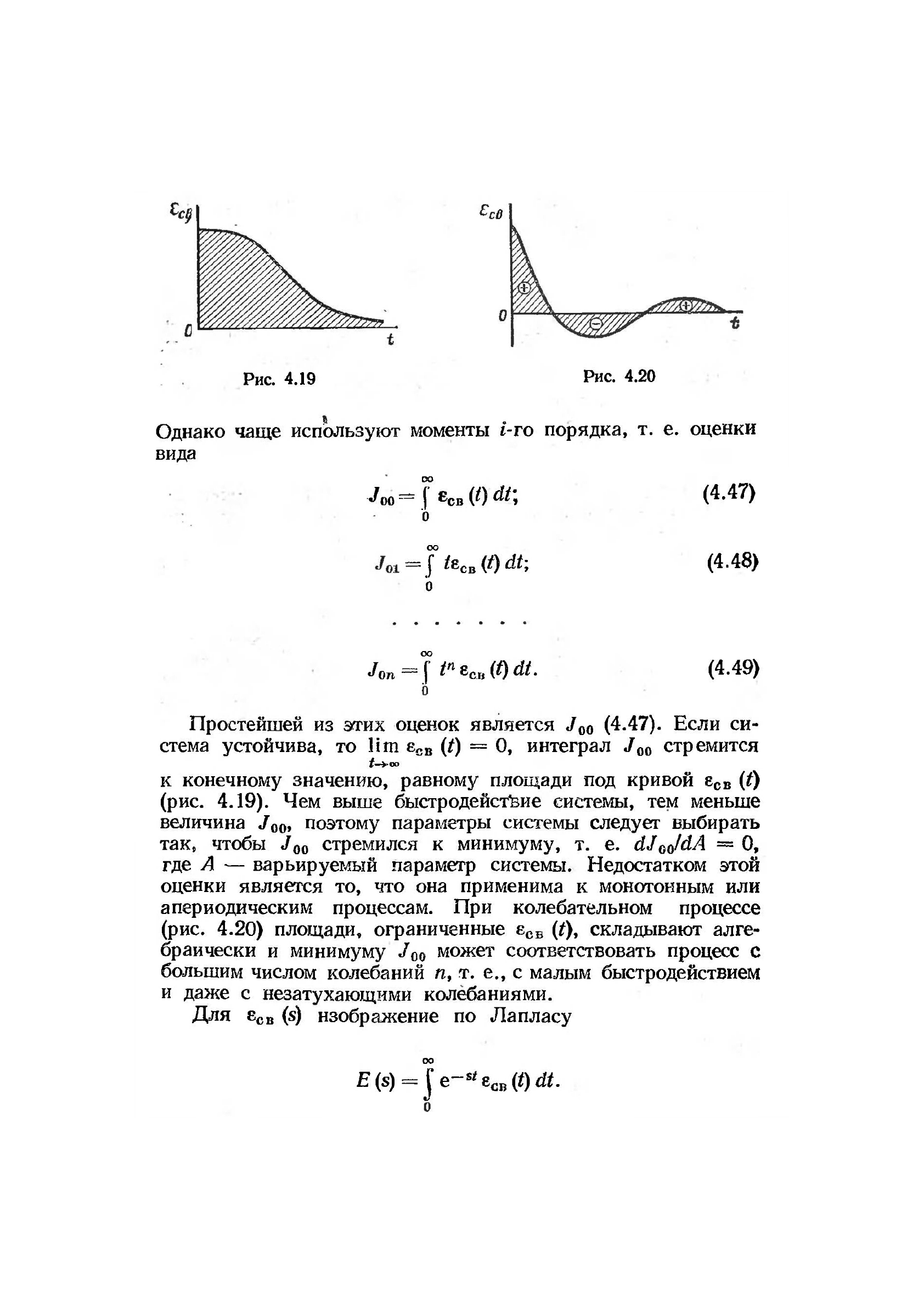
Рис. 4.19
Рис. 4.20
Однако чаще используют моменты i-то порядка, т. е. оценки
вида
оо
Л0 = (' Е
св
(0 dt\
о
(4.47)
оо
= J (t) dt;
о
(4.48)
оо
Jon - f t
n
г
си
(t) dt.
(4.49)
Простейшей из этих оценок является J
00
(4.47). Если си-
стема устойчива, то lim е
св
(/) = 0, интеграл J
00
стремится
f—Voo
к конечному значению, равному площади под кривой е
св
(0
(рис. 4.19). Чем выше быстродействие системы, тем меньше
величина /
00
, поэтому параметры системы следует выбирать
так, чтобы J
00
стремился к минимуму, т. е. dJ
00
/dA = 0,
где А — варьируемый параметр системы. Недостатком этой
оценки является то, что она применима к монотонным или
апериодическим процессам. При колебательном процессе
(рис. 4.20) площади, ограниченные е
СБ
(/), складывают алге-
браически и минимуму J
00
может соответствовать процесс с
большим числом колебаний п
9
т. е., с малым быстродействием
и даже с незатухающими колебаниями.
Для 8
СВ
(s) изображение по Лапласу
оо
Е (s) = j e-
s
' е
св
(*) dt.
о

Сравнивая это выражение с (4.47) для /
0
о? можно записать
оо
/оо = J е
св
(0 dt - Е
св
(0). (4.50)
о
Разложим e~
st
в ряд по степеням st:
е-* = 1—sf + O.Ss?*
2
.... (4.51)
Подставим (4.51) в выражение для определения Е
св
(s), т. е.
оо оо оо
£
св
(s) =
j"
е~е
св
(0 dt = J е
0в
(0 Л-sJ fe
CB
(Q
dt +
0 0 0
оо
-b0,5s
2
j*1
2
e
CB
(t)
dt —... = /
00
— sJ
cl
+0,5s
a
J
02
—... . (4.52)
о
Если разложить £"
CB
(s) по степеням s в ряд:
E
CB
(s) = £
CB
(0) + s-0,5 +
\ ds j s=o \ ds
2
/s=o
(4.53)
то, сопоставляя (4.52) и (4.53), можно сделать следующее за-
ключение, приравнивая выражения при равных степенях s:
1
Ло=£
С
в(0); J
u
= -(^гЧ
;
<
4
-
54
>
V ds J
S
= 0
^ = г
2
-) ; (4-55)
V ds
2
Js~o
Jon =(-!)" • (4.56)
V ds
n
Js= о
Если сравнить результаты (4.50), (4.54)—(4.56) с коэф-
фициентами ошибок, приведенными в § 4.2, то /
0
о — Q>» /oi —
= (—1) С
г
; Jon =•• (—1)" Сп, где С
0
, Q, С
п
— ко-
эффициенты ошибок.
Квадратичные интегральные оценки
вычисляются по формулам
оо
20 ~
0
j'
есв
(0 dt; (4.57)
оо
hi = f [есв (0 + т? ё
с
2
в
(01 (it-
(4.58)
оо
Л» f [£св (0 -!-т? е
с
2
в
(0 + ... + 8^>
2
(01
dt, (4.59)
о
где т
а>
т
п
— постоянные величины.
Оценки /
21
,..., J
2n
называют обобщенными квадратичными
оценками.
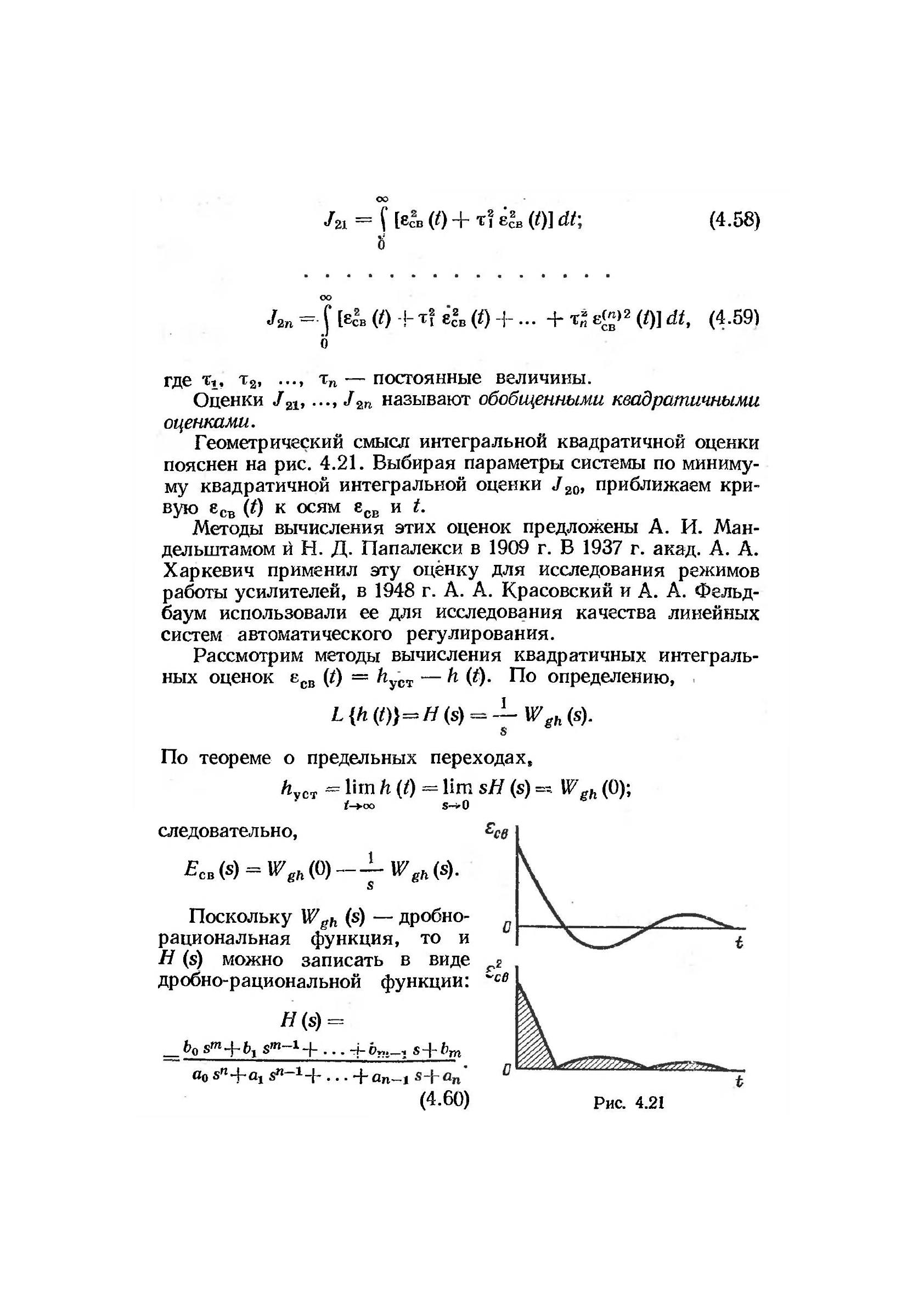
Геометрический смысл интегральной квадратичной оценки
пояснен на рис. 4.21. Выбирая параметры системы по миниму-
му квадратичной интегральной оценки J
20
, приближаем кри-
вую е
Св
(0 к осям е
СЕ
и t.
Методы вычисления этих оценок предложены А. И. Ман-
дельштамом й Н. Д. Папалекси в 1909 г. В 1937 г. акад. А. А.
Харкевич применил эту оценку для исследования режимов
работы усилителей, в 1948 г. А. А. Красовский и А. А. Фельд-
баум использовали ее для исследования качества линейных
систем автоматического регулирования.
Рассмотрим методы вычисления квадратичных интеграль-
ных оценок е
уст
св W = h
L{h(t)}~H(s)
h
(f).
По определению,
L
W
gh
(s)-
По теореме о предельных переходах,
А
уст
- liin h
{t)
= lim sH (s)
=--
W
gk
(0);
t-> oo S—>0
следовательно,
Ecn
(s)
= W
gh
(0) -W
gh
(s).
s
Поскольку W
gh
(s) — дробно-
рациональная функция, то и
Я (s) можно записать в виде
дробно-рациональной функции:
с6
#(s) =
_ 6
0
S
m
+ b
x
S
m
~
x
+ . . 8+Ьп
а
0
s
n
+% s"-
1
+ ... + a
n
-i
(4.60)
Рис. 4.21

При m < п оценку /
2
о (4.57) можно вычислить, используя
коэффициенты b
О»
••'»
Н QQJ
..., Cl
n
(4.60), по формулам, при-
веденным ниже без вывода [4]:
с»
20
j
бсв
(0 dt - jlj- (В
0
Д
0
+ В
х
Д, +... + Д
т
_
2
+
о
п
+
Вт~1
+ ^т ^т) ™ ? * »
(4.61)
где Д — определитель Гурвица, составленный из коэффици-
ентов:
Д-
«П
a
Tl-2 «П 4 ••
0
0
a
n
-1
^n—3 ••
0
0
~a„
fl
n
_a ...
0
0
0
—«n-l •••
, 0
0 0
0
... %
(4.62)
в котором все коэффициенты с меньшим индексом 0 и большим
п заменяют нулями. Определители Д
0
, Д
т
получают из
(4.62) заменой столбца (v + 1) столбцом а
п
~
ъ
а
п
0, 0, а
v = 0, 1, т.
Коэффициенты В
0
, B
lt
..., В
т
^
ъ
В
т
определяют как
е
0
— bfn,
Bi
— ^m—i
2f?
w
b
m
—
2
',
B
v
— bf
n
_
v
26,
n
—
v -f 1
— V
— 1
-+ -+2(-l rb
TYI UM—2V
F
(4.63)
Интегральную квадратичную оценку /
20
можно вычислять
по заданной частотной характеристике замкнутой системы*
Пусть Е (/со) — изображение Фурье для функции е
св
(t),
на основании теоремы свертки в комплексной области для
£ Кв (0 е
СЕ
(0) можно записать [7] при s = 0
оо
оо
<^20 ~
Г SQB (t)
dt = -i-
j" f
Е
св
(/со) I
3
do>;
(4.64)
о 0
1
e
CB
(0 = h
ycT
- h (t) = E
CB
(/to)
= [
y
W
gh
(0) - W
gh
(/to)],
(4.65)
