Волков В.Я. и др. Курс начертательной геометрии на основе геометрического моделирования

Подождите немного. Документ загружается.

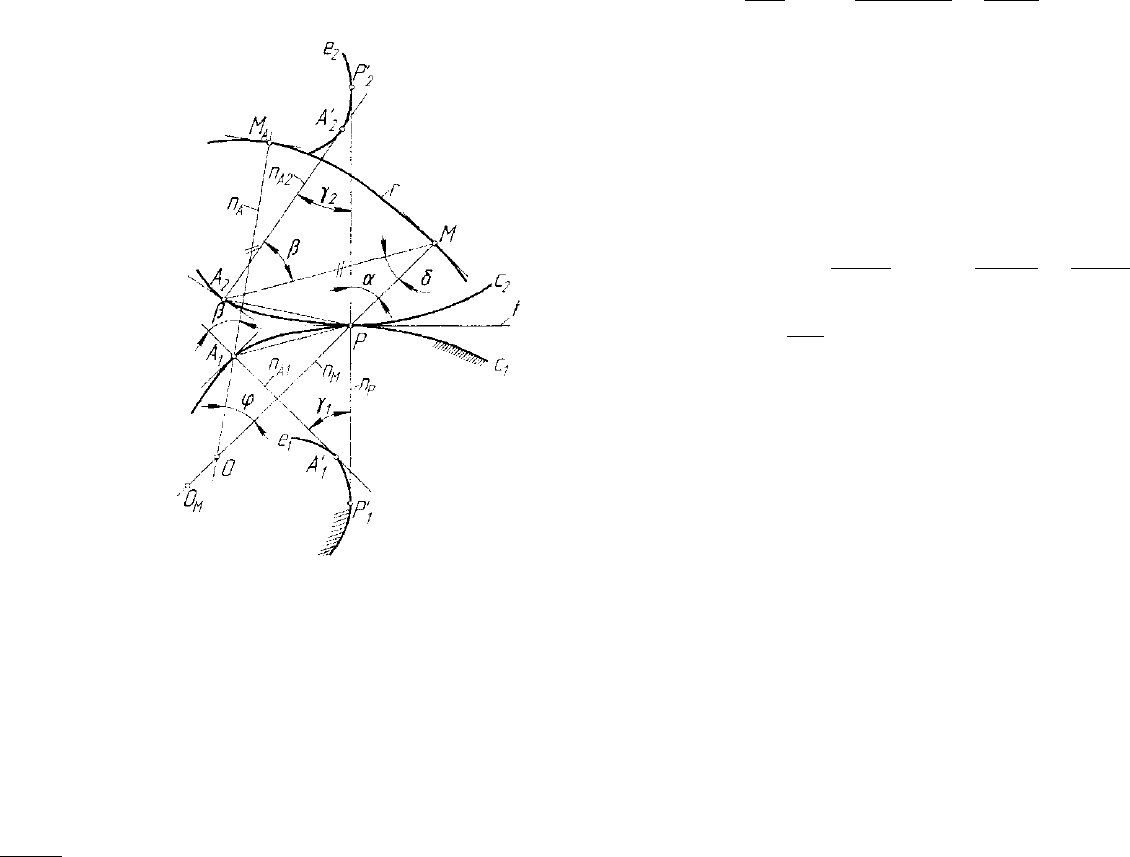
ходящей через полюс Р и общей нормалью п

центроид в точке

их касания - полюсе Р; у

~ п

л п

АХ

и у

= п

л п

Л2

- углы между

нормалями подвижной и не-

подвижной центроид;

S — п

л МА

В = МА

л п

А2

- углы, обра-

зуемые прямой МА

с норма-

лью п

рулет ты и нормалью

п ,

подвижной центроиды с

; <р - п

лп

- угол между

бесконечно близко располо-

женными нормалями рулет-

ты. Отрезок МА

становится

отрезком нормали п

, то есть

МА-, - М

, когда центрои-

ды с, и с

касаются в точке

=А

. Из геометрической

схемы следуют равенства:

<р + в = у

+а, а + 5 = В + у

Оба равенства дают одно:

(р + 5 = у

+ у

. Введем обо-

значение: As - А

Р = А

Р -

равные бесконечно малые ду-

Рис. 5.19. Схема определения

кривизны рулетты г

ги центроид с, и с

. Разделим полученное равенство сумм углов на

As и перейдем к пределам:

Urn

lim

+ lim -^- = —+ -L, где R, и R

As^oA?

AS~>O

As As-+o As

A<-»DAS

R, R-

• радиусы

кривизны центроид в точке их касания Р. Поскольку (р и sin <р - эк-

вивалентные бесконечно малые, то можно записать

,. Ф .. simp

lim — = hm . Заменяя бесконечно малую дугу As стягивающей

л*-+о As д»->о As

140

се хордой и рассматривая треугольник АРА

О, можно записать:

sine? ,. sm( ZOPA,) cos а „

lim — = lim — = . Поясним полученные равенства.

•\

->o As л*н>о QA

11ервое равенство следует из теоремы синусов для треугольника. Вто-

рое равенство следует из того, что в пределе секущая А

Р занимает

положение касательной t в точке Р касания центроид. Угол ZOPA

стремится при Д?-»0 к углу 90—а, точка Л, стремиться к точке Р,

а точка О - к центру О

кривизны рулетты г в ее точке М .

Аналогичным образом, из рассмотрения АРМА

следует:

S ,. sin 5 ,. sm(ZMPA

) cos or „ _

hm —- = hm = lim —^ — = . Таким образом, окон-

Л<!->0 As As-»0 As As->0 MA

чательно полагаем известную формулу Эйлера [8]:

cos«(—- h —) = — + * , где MP + РО

= R

- радиус кривизны

POfyi MP R

рулетты в ее точке М .

В каждый момент времени касания центроид с, и с

существуют

точки, связанные с подвижной центроидой, рулетты которых имеют

нулевую кривизну, то есть для них выполняется условие РО

= =о.

Множество таких точек представляет собой окружность, диаметр d

которой, на основании формулы Эйлера, удовлетворяет соотношению

— = -- + ^ . Положение точек этой окружности относительно полю-

d R

са Р определяется отрезком PM — d-cosa. Они являются точками

распрямления своих рулетт [8].

I [усть заданы подвижная с

и неподвижная с, центроиды и неко-

торая линия а

, жестко связанная с центроидой с

. При качении без

скольжения центроиды с

по центроиде с, линия а

будет переме-

щаться, образуя непрерывное однопараметрическое множество линий

{а

}. Огибающей множества {а

} будет некоторая линия а

, которая

по аналогии с траекторией движущейся точки, неизменно связанной

141

с подвижной центроидой с

, может быть названа неподвижной ру-

леттой, поскольку она неизменно связана с неподвижной центроидой

с,. Если центроиды с

и с

}

поменять "ролями", то есть считать не-

подвижной с

, а подвижной с

, с которой жестко связана линия а,, то

в результате обкатывания центроиды с

по центроиде с

получим

огибающую непрерывного однопараметрического множества ли-

ний {а,}, которой будет линия - рулетга а

. Таким образом, в ис-

ходном положении, когда с

и с

суть соответственно неподвижная и

подвижная центрои-

ды, линии а

и а

бу-

дут называться со-

пряженными, то есть

взаимоогибаемыми

рулеттами, одна из

которых а

{

- непод-

вижная, а другая а

подвижная рулетты

[81.

Пусть с центрои-

дами с, и с

связаны

сопряженные рулетты

и а

(рис. 5.20).

Для кривизны непод-

вижной рулетты а, в

ее точке М имеет ме-

сто вышеприведенная

формула Эйлера, ко-

торую можно преоб-

разовать, приняв сле-

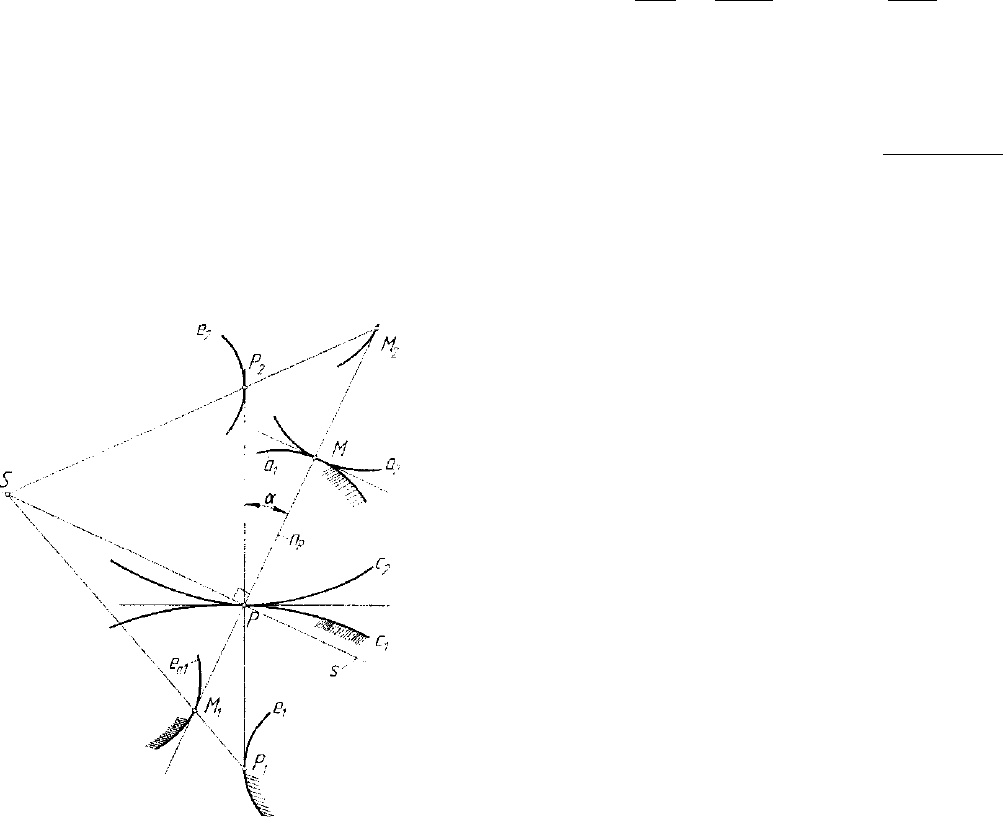
дующие обозначения:

Рис. 5.20. Построения Бобилье

142

1111 1111 ,

—i = —; = = ; -—, где a - диаметр окружно-

{

d PO

Wj MP m

сти, состоящей из точек распрямления рулетт. С учетом принятых

обозначений формула Эйлера принимает вид (— + —) • cos а- — , из

т d

тн

•

cos ct

которого следует формула т

= , в которой параметры т

т- d -cosor

и т связаны дробно - линейным соотношением. В соответствии с

обозначениями на рисунке 5.20 эти параметры представляют собой

длины отрезков т

- РМ

; т = РМ. Таким образом, при неизменных

центроидах с, и с

, и неизменном положении прямой п

- общей

нормали сопряженных рулетт, проходящей через полюс Р - точку

касания центроид с, и с

, точечному ряду {А/}, представляющему

собой однопараметрическое множество точек касания всевозможных

рулетт а, и а

на прямой п

, соответствует точечный ряд {М

}

ряд центров кривизны рулетты а

, на той же прямой п

. Это соответ-

ствие как раз и определяется вышеприведенными дробно—линейными

соотношениями. Из проективной геометрии известно, что в этом слу-

чае соответствие рядов {м}ап

и [W|}c»

является проективным

[10, 37]. Из дробно-линейного соотношения следует, что точка Р яв-

ляется в этом соответствии двойной, так как при т = 0 получаем

{

=0. Очевидно, между рядами {M}czn

и {М

}сп

также суще-

ствует проективное соответствие, следовательно, проективное соот-

ветствие существует и между рядами {М

} и {М

}, и точка Р являет-

ся двойной, то есть самосоответствснной в проективном соответствии

этих рядов. Очевидно, пучок прямых (Fj), проецирующий ряд {М,},

и пучок прямых (Р

), проецирующий ряд {М

}, проективны, по-

скольку проективны ряды, которые проецируют эти пучки [10, 37].

Поскольку точка Р является двойной в проективном соответствии

рядов {Mj} И {М

}, ТО двойной будет и прямая Р

, соединяющая

центры проективных пучков прямых, то есть она соответствует сама

себе. В этом случае, как известно [10, 37], проективные пучки прямых

143

(Р,) и (Р

) перспективны, то есть их соответственные лучи пересе-

каются в точках на оси перспективы. Из теоремы Бобилье следует,

что осью перспективы служит прямая SPA.PM [8]. Из сказанного

следует, что центры кривизны центроид с,, с

и центры кривизны со-

пряженных рулетт а, и а

связаны конструктивно простым построе-

нием Бобилье, которое позволяет при заданных центроидах и одной

из рулетт в их контактном положении (М - точка контакта) опреде-

лить кривизну другой рулетты в ее отсутствие. Например, требуется

определить при указанных данных кривизну рулетты о

. Необходи-

мые построения выполняются в следующей последовательности:

sLrip, P-^MjClx = S, SP

[\n

- M

, M

- искомый центр кривизны

рулетты а

Построение Бобилье позволяет получить известную в теории

плоских зубчатых зацеплений формулу Эйлера-Савари. Введем сле-

дующие обозначения

(рис. 5.21): \1М. Л" - *^ЛА

радиус кривизны нспод- ,

вижной рулетты а,, /

\f.\t • = R" - радиус j \ /

кривизны подвижной

рулетты а

; РМ=т.

В таком случае по-

лучаем РМ

=т + R",

РМ

= R'-m. Поскольку

геометрическая схема на

рисунке 5.21 отражает

геометрическую карти-

ну мгновенного состоя-

ния, то вполне возмож-

ны замены подвижной

рулетты а

ее центром

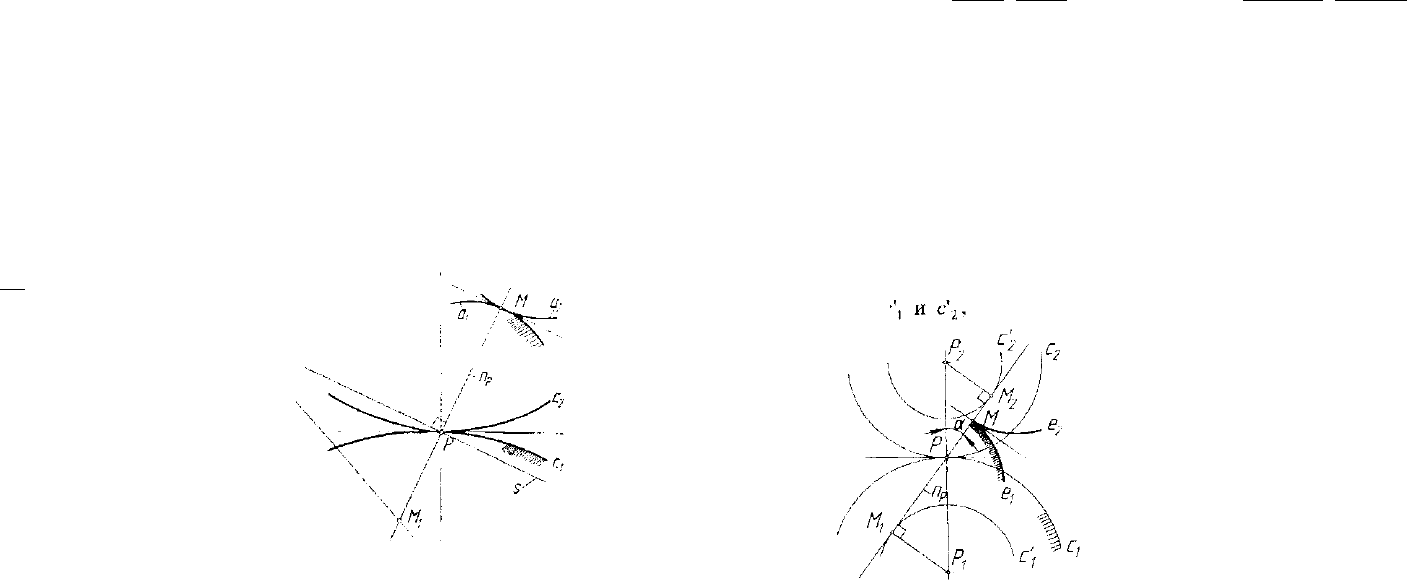
Рис. 5.21. Схема вывода

уравнения Эйлера-Савари

144

кривизны М

, а неподвижной рулетты линией а\, описываемой

центром кривизны М

при огибании подвижной рулетты а

непод-

вижной сг, в процессе обкатывания подвижной центроиды с

по не-

подвижной С]. В таком случае точка М

может быть принята в каче-

стве подвижной точки, неизменно связанной с центроидой с

и опи-

сывающей рулетту а\. Применяя на этом основании ранее приведен-

ную формулу Эйлера, получим:

' i

1 1

-и

1 1

cosa( + ) = — или же —— + = .

РМ, М~,Р d R-m m+R" dcosa

Последнее выражение представляет собой известную формулу

Эйлера-Савари [8]. Очевидно, схема на рисунке 5.21 позволяет гео-

метрическими построениями определить кривизну рулетга а\ в дан-

ной ее точке М

. Последовательность построений следующая:

s ±РМ

, M

[)s = S, SP

0,n

= М,, М, - искомый центр кривизны

рулетты и\. Рассмотрим пример применения формулы Эйлера-

Савари. Предположим, что с, и с

- неподвижная и подвижная цен-

троиды радиусов К, и R

соответственно (рис. 5.22). Проведем через

полюс Р наклонную прямую п

под углом а и построим две окруж-

ности с

Рис. 5.22. Сопряженные

рулетты цилиндрической

зубчатой передачи

касающиеся этой прямой. Для любой точки М е п

построим эвольвенты е

{

и е

окружно-

стей с'| и с\ соответственно. Пока-

жем, что эвольвенты е

и е

могут-

быть приняты в качестве сопряженных

рулетт, то есть для них выполняется

формула Эйлера-Савари. Для элемен-

тов этой формулы, в соответствии с

рисунками 5.22, можно записать:

=R", РМ=т, ММ

=R'. В та-

ком случае поучаем: РМ

=m + R" =

= P

-cos«; РМ

}

= R'-m - R

-cosа.

Окончательно, можно записать:

145

1 ]_ Д

(

1 , 1

Л'-/?г m+R" Rycosa R

cosa cos a R

J cos a

Этим примером Л. Эйлер в 1767 г. впервые обосновал возможность

использования эвольвенты окружности в качестве профилей зубьев

цилиндрической прямозубой зубчатой передачи с параллельными

осями колес.

5. /. 7. Касание кривых (элементы дифференциальной геометрии)

Довольно часто в результате выполнения теоретического иссле-

дования либо эксперимента получается массив точек на плоскости и

возникает задача проведения линии через упорядоченный массив то-

чек либо линии через определенные точки с заданными в них допол-

нительными условиями: положением касательной прямой, значением

кривизны и др. Кроме того, иногда требуется заменить заданную ли-

нию другой линией по определенным условиям замены. Подобные

задачи относятся к задачам аппроксимации, то есть когда требуемся

заменить одну функцию, заданную массивом точек, графически либо

уравнением, другой функцией, удовлетворяющей определенным ус-

ловиям. Известны следующие основные методы аппроксимации

функции [15, 18]:

1. Интерполирование, когда требуется провести кривую через

определенные точки исходной кривой;

2. Приближение функций, когда исходная функция на множест-

ве ее точек заменяется другой функцией с использованием опреде-

ленного критерия приближения, например, минимизация суммы

квадратов отклонений аппроксимирующих и исходных значений

функции:

Ziy'i^

Уаппрок)

= т'п;

/=1

3. Построение обвода, представляющего собой составную кри-

вую, используемую в качестве аппроксимирующей линии, при этом

под обводом понимается линия, составленная из дуг кривых одного

или различных видов, в точках стыковки которых должен быть вы-

держан определенный порядок гладкости (порядок касания).

146

Рассмотрим основные положения теории касания плоских кри-

вых, известной в дифференциальной геометрии [26] и ее приложениях

|8], с точки зрения их практического применения. Пусть имеем две

кривые а и а

с общей точкой А

А,

а,

(рис. 5.23), уравнения которых следую-

щие: у = f(x) - для кривой а, у = f

(x)

- для кривой а

. В соответствии с теори-

ей касания кривых, необходимым и дос-

таточным условием касания не ниже п —

го порядка кривых а и а

в их общей

точке Ад [х

; у

= Дх

) = f

(х

)] являет-

ся совпадение производных в этой

точке: f(x

) = f\ (х

);/"(*о) = f\ (x

); ..-.fix,) = /,"(*„)•

Пусть на плоскости задано множество кривых (я,}, описываемое

уравнением у = f

(x\с,,с

,...,с

). На кривой а выберем п точек:

, А

,А

. Подберем значения параметров с

,с

,...,с„ так, чтобы

кривая я, множества {а

\ проходила че-

рез эти п точек (рис. 5.24). Эти значения

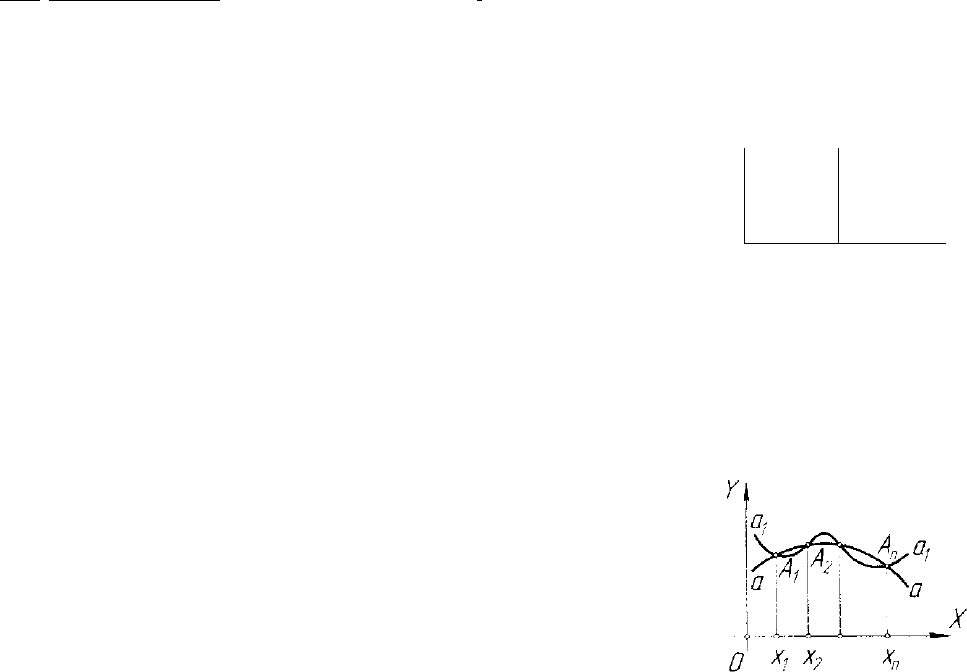
Рис. 5.23. Касание кривых

,.(1) J2)

1 '2 '

., с„ ' параметров определяют-

ся из условий: /(х,) =/, (х,),

f(x

) = f

), f(x„) = f

(x„). Вве-

дем в рассмотрение функцию

fi{x) = f(x)- /, (х). Так как имеют место

равенства /л(х

) - ju(x

) =... = fi(x

) = 0,

и функция /л(х) непрерывна на отрезке

[х

, х

] и дифференцируема в каждой внутренней точке этого отрезка,

поскольку эти условия выполняются для каждой из функций /(х) и

/(х,), то по теореме Ролля о корнях производной получим:

Рис. 5.24. Пересечение

кривых

,0)

где

Х^ ^ Х-^ _Х"2 *С Х^ *^

<...<х„

< х„

Применив теорему Ролля для функции //(х), полу-

147

чим: M"(xi

) = м"(х?

)

) = -=М"(х<

%) = °>

<*\

2° <

< х[

<...< х

}

л-1- И так далее. В итоге получаем:

^С-').(*(»-'))

= 0> Г

де x

(и

<Jc

(и

<xf

•

. Устремим все точки

/4,, Л

,кривой а к ее точке А

(х

), то есть выполним предель-

ный переход lim JC, = lim х

- ... — lim х

- х

. В этом случае параметры

с\

]

\с

\...,с^ будут стремиться к своим предельным значениям

(0)

,с

°\...,с

. В итоге отрезок со всеми своими точками бу-

дет стягиваться в точку х

. В пределе для всех вышеприведенных

производных

/и'(х),

fi"(x),

fj"~

{x)

получим: fj'(x

(]

)

/j"(x

)

= ... - ju"~

]

), что соответствует необходимому и достаточному ус-

ловию касания не ниже (п -1)—го порядка кривых а и я,, также при-

веденному выше. Из вышеизложенного следует важный результат о

том, что две алгебраические кривые порядков тип могут иметь ме-

жду собой касание не выше (W-W-I)-JO порядка, поскольку по тео-

реме Безу они пересекаются в (т-п) точках и, следовательно, любая

из них может проходить не больше чем через {т-п) бесконечно близ-

ко расположенных точек другой.

Рассмотрим примеры.

1. Соприкасающаяся прямая. Пусть имеем прямую общего по-

ложения относительно декартовой системы координат в плоскости:

у - с,х + с2. Так как п = 2, то соприкасающаяся прямая может иметь с

кривой касание не ниже первого порядка. Прямая является касатель-

ной к кривой у- f(x) в некоторой ее точке (х

,>>

). Действительно.

с,х

+ с

- у

= f(x

); у'„ = Г (*о) =

\; с г = У о

У'о '

о • Таким обра-

зом, получаем: у - у

'(х~ х

) + у

. Очевидно, что имеет место усло-

вие у"- О для рассматриваемой прямой. Точки кривой у - /(х), в ко-

торых /"(х) = 0, называются точками распрямления. В этих точках

касательная к кривой проходит через три бесконечно близкие точки.

2. Соприкасающаяся окружность. Из уравнения окружности

(х-a)

+(y-b)

-R

= 0 следует, что и = 3. Поэтому окружность с

148

кривой y~f(x) может иметь касание не ниже второго порядка. Из

уравнения окружности можно получить последовательным диффс-

реш 1ированием следующие уравнения: (у~Ь)- у'+(х - а) = 0;

(у -

И) • .У"+(У

)

+1=0.

По

приведенным выше необходимым

и дос-

I аточным условиям касания не ниже (и - 1)-го порядка кривых в точ-

ке (х

,У

) принимаем у = Дх

); у'=/'(х

); /'=/"(>„), где

v = f(x) - уравнение некоторой кривой. Из трех приведенных урав-

нений для окружности и уравнения кривой у = f(x) следуют уравне-

ния трех параметров окружности, соприкасающейся с кривой в точке

[] + (y)

lv i + (V)

„ [i + (/)

]

3/2

„

): a = x-

КУ

• ; в = у + —V -;

= .. '

Если

V У У

у= f"(x

) = 0, то искомой окружности в точке (х

,у

) кривой

V = /(х) не существует, поскольку эта точка - точка распрямления

кривой.

Эти уравнения совпадают с известными уравнениями, опреде-

ляющими окружность кривизны кривой в некоторой ее точке (л\у).

Таким образом, соприкасающаяся окружность является окружностью

кривизны кривой линии. С другими кривыми второго порядка окруж-

ность пересекается в четырех действительных точках. Следовательно,

на основании сделанного выше вывода о касании двух алгебраиче-

ских кривых, она не может иметь с ними касание выше третьего по-

рядка. В вершинах кривых второго порядка, в которых их кривизна

достигает экстремума, соприкасающаяся окружность имеет касание

третьего порядка, то есть она проходит через четыре бесконечно

близко расположенные точки этих кривых.

3. Соприкасающаяся парабола. Пусть задана парабола с осью,

параллельной оси OY: у = с, + с

х + с

. Очевидно, что /7 = 3. Сле-

довательно, такая парабола может иметь с кривой у - f(x) касание

не ниже второго порядка. Из уравнения параболы, соприкасающейся

с кривой _у = f(x) в точке (х

,у

) можно получить следующие урав-

149

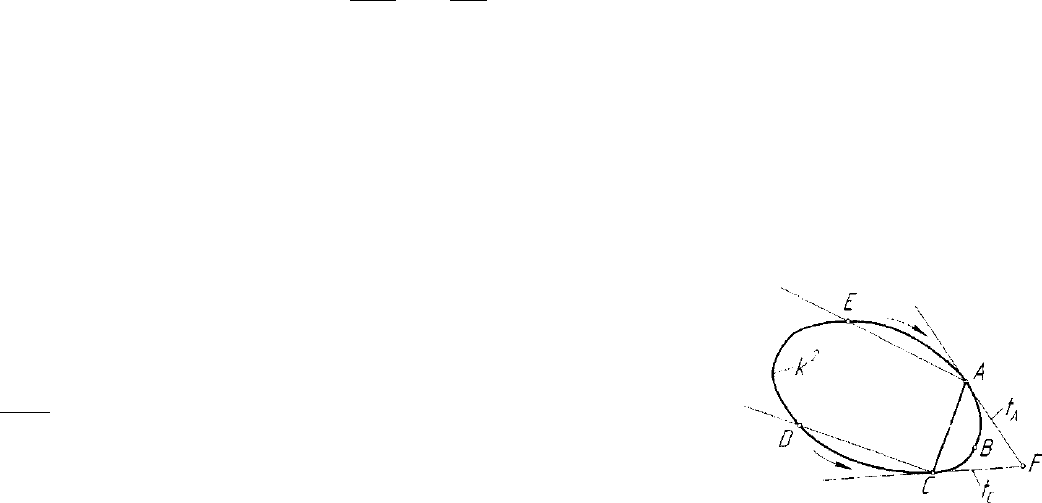
нения для определения коэффициентов: /(х

) = с

}

+с

;

f'(x

) = с

+ 2с

; /"(*

) = 2с

4. Соприкасающийся эллипс. Для эллипса с осями, параллель-

,х-с ,

,j-tf\-> .

ными координатным осям, можно записать: ( ) +(- )"=1,

a b

2 2 2 2 2 2

Z> (х - с) + а (у - d) -а Ъ = О. Согласно последнему уравнению

следует л = 4. Поэтому, такой эллипс может иметь соприкосновение с

кривой у = f (х) не ниже третьего порядка. Трижды дифференцируя

последнее уравнение эллипса, получим следующие уравнения:

(у - d) • y'+b

(x - с) = 0; а

(у - d) • у"+а

• (у

)

+ Ь

= 0;

0>-</)-У"+зуУ'=о.

Из этих уравнений, с учетом исходного уравнения соприкасаю-

щегося эллипса, могут быть получены его параметры а, Ь, с, d.

Аналогичным образом, как и в случае эллипса, может быть рас-

смотрена соприкасающаяся с кривой у — f (х) гипербола с осями, па-

раллельными координатным осям, описываемая уравнением

/>'~^ч2 ,

( _ ^ ) = 1, и найдены, в результате трижды выполняемого

a b

дифференцирования, се параметры а, Ь, с, d.

5.1.8. Конструирования обводов из дуг кривых второго порядка

Известно множество способов конструирования обводов точек на

плоскости. Основными из них, поучившими наибольшее практиче-

ское применение, являются [16]:

1. Радиусографический, когда через упорядоченный массив то-

чек проводится обвод первого порядка гладкости, состоящий из дуг

окружностей разных радиусов, имеющих в точках стыка общие каса-

тельные;

2. Способ кривых второго порядка, когда обвод составлен из дуг

кривых второго порядка, имеющих в точках стыка общие касательные

150

(обвод первого порядка гладкости) или равные значения кривизны

(обвод второго порядка гладкости);

3. Сплайн - аппроксимация.

Доказано, что ось изогнутой гибкой тонкой линейки (spline), про-

ходящей через заданные точки, описывается полиномом третьей сте-

пени у = а

+ а

х + а

+ а,х

, представляющем уравнение кубиче-

ской параболы. Эта парабола может быть задана: четырьмя точками,

двумя точками и касательными в них. Обвод первого и второго по-

рядков гладкости составляется из дуг кубических парабол. Если, на-

пример, заданы две точки (х

,у,) и (x

i+x

), и две касательные в

них (у))'

и (у,-,,)',, то этими условиями, согласно уравнению кубиче-

ской параболы, могут быть определены четыре коэффициента в урав-

нении кубической параболы. Дуга полученной параболы пройдет че-

рез эти две точки с касательными к параболе в них [18].

ки, например, D и Е, устремит ь

коники к

каждую к соответствующей точ-

ке: D—>С, то предельным положением секущей ЕА станет

коники. Получаем переход от задания коники пятью точками к ее за-

данию тремя точками и двумя касательными в них. Образующийся

треугольник FAC называется касательным треугольником коники.

Этот треугольник положен в основу известного способа инженерного

дискриминанта, применяемого для конструирования обвода первого

порядка гладкости из дуг коник [15]. Предположим, задан ряд точек

Рассмотрим теоретические

положения, составляющие осно-

ву конструирования обводов из

дуг кривых второго порядка. Как

известно, кривая второго поряд-

ка (коника) определяется зада-

Рис. 5.25. Касательный треугольник

нием в плоскости пяти точек

A,B,C,D,E общего положения

(рис. 5.25). Если две точки кони-

касательная t

в точке А, а секущей DC - касательная t

в точке С

151

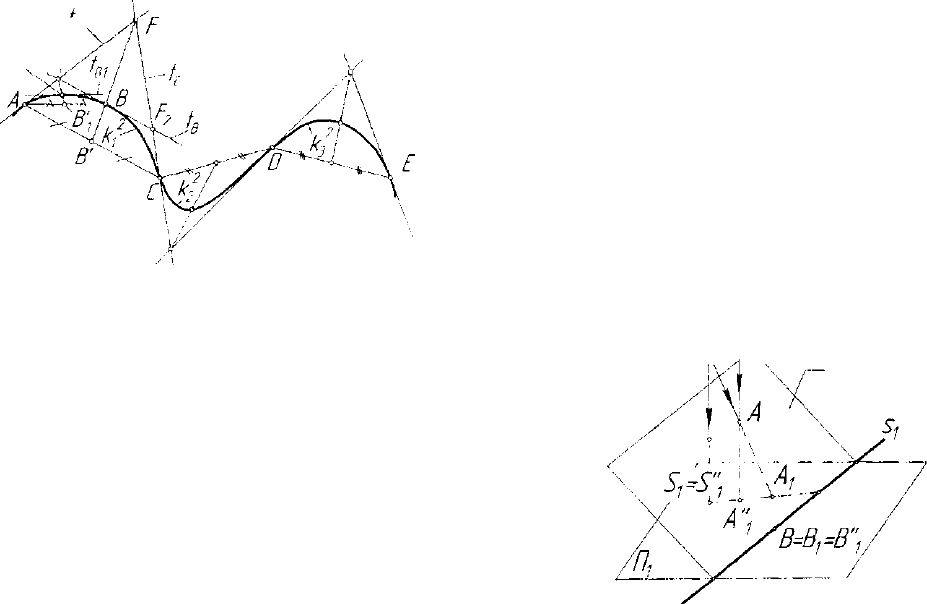
А,С, D, Е,... и положения касательных t

в них

(рис. 5.26). Требуется провести через эти точки указанный обвод. Ес-

ли в касательном треугольнике AFC провести медиану FB' и вы-

брать на ней некоторую точку В, то в зависимости от значения отно-

шения ВВ': FB=d получим различные возможности для проведения

дуги ABC коники: d = 0,5 - дуга параболы к{, d > 0,5 - дуга гипер-

болы к

, d < 0,5 -

дуга эллипса к

. /

Выбрав одно из трех д

возможных значений

инженерного дис-

криминанта d, по-

лучим определенную

точку В на медиане

FB' и, следователь-

но, дугу определен-

ной коники кг, оп-

Рие. 5.26. Обвод первого порядка иадкости

из дуг коник

ределяемои усло-

виями: A,t

; B;C,t

После проведения касательной t

, параллельной стороне АС, полу-

чаем новую пару касательных треугольников AF

{

B и BF

C. В каж-

дом из них выполняются построения, подобные построениям точки В

в треугольнике AFC. Для треугольника AF

{

B это будет точка #,.

Последующие проведения касательных через полученные точки В

коники к

внутри треугольников указанной пары (например, t

II АВ

) приводит к образованию новых четырех касательных треугольников

и т.д. Описанный процесс конструирования дуги коники к

продол-

жается до получения требуемого числа ее точек. Затем выполняется

по описанному алгоритму построение дуги коники к\ и дуги коники

к\. Очевидно, сконструированный обвод из дуг коник к

, к

представляет собой обвод первого порядка гладкости.

152

Зададим следующий аппарат отображения (проецирования) про-

странства Е

(рис. 5.27):

1. Центры проецирования 5 и S"

(несобственный);

2. Плоскость проекции Я,.

Плоскость А пространства при таком аппарате проецирования

будет моделироваться на плоскости проекций П

гомологией

(£,,«,,4 <-> А'\), где S

- неизменный для всех плоскостей А про-

странства центр гомологии, s

- ось гомологии, А] о А'\ - пара со-

ответственных точек, моделирующая точку Ае А. Пусть плоскости

А принадлежит некоторая линия к . Очевидно, линии k

и к'\ в

плоскости Я,, полученные проецированием линии к из центров S и

5"^ соответственно, будут гомологично соответственны. В итоге ли-

ния к может моделироваться на плоскости проекций Я, следующи-

ми способами:

1. Одной проекцией или к", и гомологией (S,,^,/!, о Л", ),

где А

о Л", - модель любой

'~^"\ точки плоскости А в указанной

Рис. 5.27. Моделирование плоскости гомологии s, и пары гомологич-

гомологии.

54 ^

2. Одной проекцией А, или

к'\ и тремя парами проекций

«-» /4",, #j <н> С, <->Г",

трех различных точек А, В и С

плоскости А .

Очевидно, при неизменном

центре 5, гомологии модель

любой плоскости пространства

будет определена заданием оси

пространства гомологией

ных точек в плоскости Я,.

153

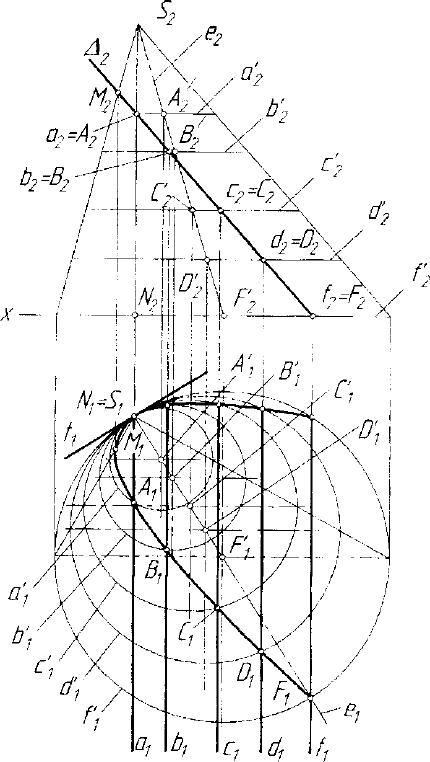
Рассмотрим эллиптический конус второго порядка, у которого

одно из двух семейств окружностей таково, что плоскости окружно-

стей этого семейства перпендикулярны одной образующей

SN(S

) этого конуса (рис. 5.28). Если расположить этот ко-

Рис. 5.28. Пучок гомологии с инвариантными центром 5 и коникой к

пус относительно плоскости проекций 77, так, чтобы выполнялось

условие SN L 7/,, то указанное семейство окружностей отобразится

на плоскость 77, в пучок окружностей, проходящих через точку

.V, =5) с общей касательной t

{

. Проведем некоторую проецирующую

плоскость A А. П

, пересекающую рассматриваемый конус. Очевид-

но, что линией пересечения будет некоторая коника к

(к

,к

). Ее ор-

тогональная проекция к

также будет коникой, поскольку при орто-

гональном проецировании в общем случае порядок алгебраической

кривой и порядок ее проекции равны. Коника к

пересекает каждую

окружность а\ , в\ , с\ , d\ , f\ , ... пучка окружностей в четырех точ-

ках: одной двойной (гонка касания S

{

с общей касательной t

) и двух

простых точках. Прямые, соединяющие пары простых точек пересе-

чения, образуют пучок параллельных прямых а, II в

II с, II d

II /,

поскольку каждая из этих прямых представляет собой ортогональную

проекцию линии пересечения плоскости А и плоскости из пучка па-

раллельных плоскостей, которым принадлежат окружности рассмат-

риваемого семейства на конусе. Очевидно, каждая из окружностей

а'(а\ ,а\ ),b'(b\ ,b'

),... может быть рассмотрена как центральная

проекция коники к

(к

,к

) на плоскость этой окружности из центра

S(S

]

), а сама коника к

(к

,к

_) может быть рассмотрена как цен-

тральная проекция каждой из этих окружностей на плоскость А ко-

ники к

На плоскости 77, получаем пучок гомологии с инвариантным

центром 5, и инвариантной коникой к

с параллельными осями го-

мологии а,, в,, с,, d

, f

, ... В каждой гомологии образом соответст-

вующей окружности является одна и та же коника к

. Ось гомологии

проходит через точки пересечении этой окружности и коники к

. Для

предельной окружности а\ пучка окружностей, то есть для окружно-

го

154

сти кривизны коники к

, ось гомологии а

проходит через центр S, -

точку касания коники к

и всех окружностей пучка.

Таким образом, анализ вышеизложенных построений позволяет

утверждать о том, что каждая из окружностей, соприкасающихся с

коникой в одной и той же точке, гомологична этой конике; точка ка-

сания есть центр гомологии; оси пучка гомологии образуют пучок па-

раллельных прямых. Это особенное гомологичное свойство коники

известно в теории обводов точек на плоскости [18], но здесь оно

получено не из косвенных, а из прямых, более простых и наглядных

рассуждений.

Рассмотрим применение гомологичного свойства коники к

для

построений дуг коник, используемых при конструировании обводов

первого и второго порядков гладкости. Предположим, что заданы

точки S,A и В коники к

и ее касательные t

и t

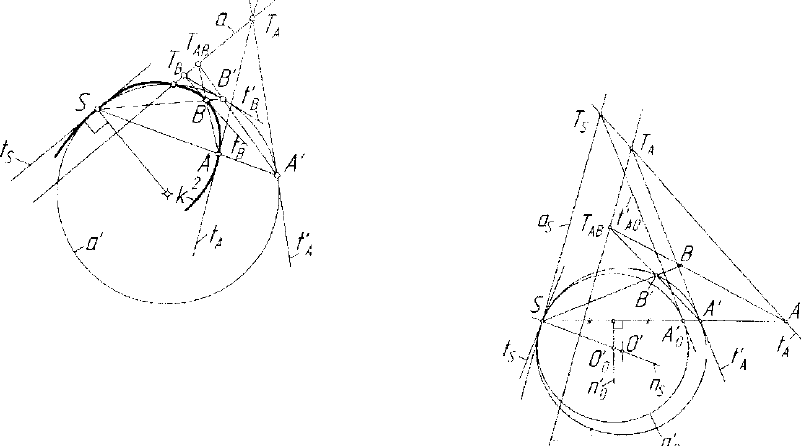
(рис. 5.29). Требу-

ется построить конику. Ясно,

что этих условий достаточно

для построения коники к . Из-

вестны решения рассматривае-

мой задачи, например, решение,

основанное на проективном

подходе [37]. Применим гомо-

логичное свойство коники для

решения рассматриваемой зада-

чи. Проведем окружность d

произвольного радиуса, сопри-

касающуюся с коникой в точке

S. Очевидно, точка S может

быть принята в качестве центра

гомологии. Определим ось гомологии а. Для этих целей построим

точки A'-SAf]a' и В'- SBf]a', представляющие собой образы точек

А е к

и В е к

в гомологии. Прямые АВ и А'В* определяют первую

Рис. 5.29. Построение коники к" на

основе соприкасающейся окружности

156

точку Т

АВ

оси а гомологии: Т

АВ

= ABf] А' В'. Проведем касательную

в точке А'еа'. Точка пересечения касательных T

f)t'

пред-

ставляет собой вторую точку оси а гомологии. Действительно. При

миться к точке А' по окружности а', поскольку в пределе прямая го-

мологичного соответствия ВВ' совпадает с прямой гомологичного

соответствия АЛ', а хорды АВ коники и А'В' окружности станут ка-

сательными t

и f

. Поэтому касательные в соответственных в гомо-

логии точках коники и окружности пересекаются в точке на оси го-

мологии. Таким образом, гомология определена центром S, осью а

и парой соответственных точек В и В' или А и А'. Задание гомоло-

гии и окружности а' позволяет построить ее образ к

, который явля-

ется искомой коникой.

Если в условии рассматриваемой задачи вместо точки В ввести

значение кривизны конструируемой коники в се точке S, то для кон-

струирования коники необходимо провести окружность кривизны а'

в точке S. Поскольку в этом случае ось гомологии а

проходит через

стремлении точки В к точке А по конике к

, точка В' будет стрс-

центр S, то для построения еще

одной ее точки достаточно опреде-

лить точку пересечения касатель-

ных t

и t'

в соответственных

точках коники и окружности кри-

визны йг'

. Задание центра S гомо-

логии, оси гомологии S еа

, ок-

ружности кривизны а'

в точке S

коники и точки А этой коники по-

зволяет построить по этим услови-

ям конику к

с заданной кривиз-

ной в ее начальной точке S.

Рис. 5.30. Определение окружности

кривизны коники

а а'

а'

Из анализа вышерассмотрен-

ной геометрической схемы образо-

вания пучка гомологии на плоско-

157

сти Я, (рис. 5.28) следует, что если провести jry4 из центра 5,, пере-

секающий окружности пучка, то касательные к окружностям пучка,

проведенные в точках их пересечения с этим лучом, будут параллель-

ными. Это свойство касательных позволяет получить решение сле-

дующей задачи. Пусть заданы три точки S, В, А коники и касатель-

ные t

и t

к ней в точках S и А (рис. 5.30). Требуется определить

кривизну коники в ее точке S. Для решения задачи построим произ-

вольную окружность d из пучка окружностей с общей точкой S и

касательной t

в ней. В соответствии с решением предыдущей задачи

(рис. 5.29), построим ось а гомологии с центром S, в которой обра-

зом окружности а' будет коника к

, определяемая условиями:

S,t

;A Л

; В. Проведем ось a

другой гомологии по условиям:

//a; Sea

. В новой гомологии с центром S и осью a

образом

искомой окружности а'а кривизны будет та же коника к

. Дальней-

шие построения выполняются в следующей последовательности:

/%П% -Tv: T

er',,,, t\

!it'

(по свойству касательных окружностей

щчка. провод.-:? кых в точках пересечения этих окружностей с лучом,

выходящим из их обшей точки касания S); SAC\t\

= А'

;

f)n

= 0'

, где п'

- срединный перпендикуляр отрезка SA'

, n

нормальная прямая (n

,SeN

). Таким образом, точка О',, - иско-

мый центр окружности кривизны а\, коники к

в ее точке S .

Эта и предыдущая рассмотренные задачи могут быть положены в

основу конструирования обвода второго порядка i ладкостн из дуг ко-

ник с общим значением кривизны в точках их стыка.

Множественные теоретические аспекты и нюансы различных ал-

горитмов конструирования обводов различных порядков гладкости из

дуг коник и других плоских кривых, а также аналитическое описание

сплайн-аппроксимации и сплайн-интерполяции можно найти в рабо-

тах [16, 18].

158

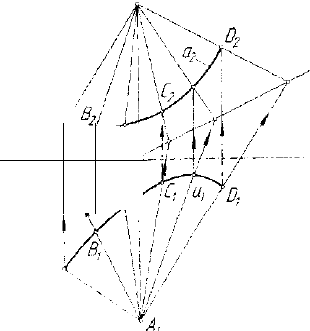
5.1.9. Моделирование плоской кривой па чертеже Монжа

п, /

п,

В общем случае моделирование плоской кривой линии, принад-

лежащей плоскости общего положения, основано на модели этой

плоскости, которая на чертеже Монжа представляет собой родство.

А Тогда пара ортогональных

проекций плоской кривой

линии на чертеже Монжа

d может быть рассмотрена как

два точечных ряда, соответ-

ственных в этом родстве. За-

дание одной проекции a

плоской кривой и задание

родства (d,A

{

<+A

), моде-

лирующего плоскость этой

кривой, позволяет построить

вторую проекцию а

кривой

(рис. 5.31). Таким образом,

Рис. 5.31. Модель плоской кривой плоская линия пространства

на чертеже Монжа может моделироваться на

чертеже Монжа следующим образом:

1. Родством, моделирующем плоскость этой кривой, и одной из

проекций а, или а

;

2. Одной проекцией а, или а

и тремя парами соответственных

в родстве, моделирующем плоскость кривой, точек, например:

Я, +>В

, В, еа,, В

еа

; С, <-»С

, С

еа

{

, С

еа

; D, f>D

, D, е о,

, D

е а

5.2. Пространственные кривые

В учебных изданиях по начертательной геометрии пространст-

венным кривым линиям уделяется незначительной внимание. Исклю-

чение составляет учебник [2]. Очевидно, это связано с тем, что тради-

159