Волков В.Я. и др. Курс начертательной геометрии на основе геометрического моделирования

Подождите немного. Документ загружается.

дожить следутощии алгоритм конструктивного решения рассматри-

иаемой задачи:

1. h<=T,:h

// X,h

-^ /г,;

2. /cIi/.M./^/j;

3. т

L f

Прямая m(m

) является решением задачи, то есть от_1_£, по-

скольку от 1 h, ml. f, где h, f - линии уровня в плоскости £. Отме-

тим, что н общем случае пары перпендикулярных прямых т A. f и

от _1_ /? - это пары скрещивающихся прямых.

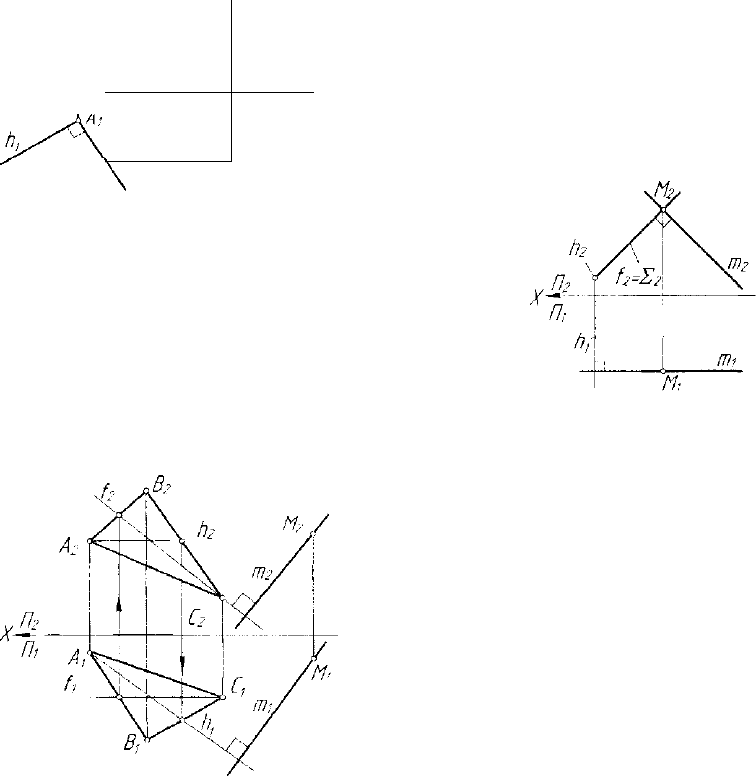
Рассмотрим решение задачи при

частном положении плоскости 2.

Пусть заданы: Е

- след плоскости

£±Я

и точка M(M

)ezZ

(рис. 4.14). Требуется построить пря-

мую т по условиям: М е от, от _L X. На

основании вышеизложенного можно

предложить следующий алгоритм ре-

шения задачи:

Рис. 4.14. Модель построения

прямой,перпендикулярной

плоскости частного положения

1. т

L /

, М

£ т

, где /

= 2U;

2. (•)/>? е /

, /г

-> я, : ± Z, (•)/?, е /г,;

3. от, _L /г,, М, е от,.

Прямая т(т

,т

) является реше-

нием задачи, то есть от _L £, поскольку т Lh,m L f, где h, f - ли-

нии уровня в плоскости £.

4.6. Перпендикулярность плоскостей

Две плоскости в пространстве Е

полу перпендикулярны, по-

скольку степень их перпендикулярности на основании формулы (1.8)

0 + 1 1

равна /7

= —. В стереометрии известен признак перпендику-

лярности двух плоскостей, выраженный теоремой [7]: если одна из

двух плоскостей проходит через прямую, перпендикулярную к

другой плоскости, то такие плоскости перпендикулярны. Очевид-

но, здесь под перпендикулярностью следует понимать именно полу-

перпендикулярность двух плоскостей. В соответствии с признаком

перпендикулярности при заданных плоскости и перпендикуляре к ней

101

11остроения, соответствующие теореме о проекции прямого угла,

приведены на рисунке 4.12. В первом случае по условиям теоремы

прямой угол 1ь4а - 90°

отображается без иска-

жения на плоскость про-

екций Я,, поскольку h -

горизонталь. Во втором

случае прямой угол

ZfBb = 90° отображает-

ся без искажения на

плоскость П

, посколь-

/5!г//Х

/7;

f? /

/7/х

ку / - фронталь в плос-

кости угла.

Рис. 4.12. Модель теоремы о проекции

прямого угла

Рассмотрим решение задачи о перпендикулярности прямой и

плоскости. Пусть на графической модели заданы: плоскость общего

положения 2,(ААВС) и точка M(M

)^L (рис. 4.13). Требуется

построить прямую т по условиям: Мет, »гХХ. Выполним анализ

условий задачи. Для этих целей используем результаты анализа усло-

вий, приведенных в пункте 4.3. Параметрическое число прямой линии

пространства Е

равно Д'"=4. Размерность условия прохождения

прямой линии через точку пространства равна O

ofl

(e\

)-2. Пред-

ставляя символически условие

перпендикулярности прямой и

плоскости, как е

'д и учиты-

вая, что степень их перпенди-

кулярности равна 1, определим

по формуле (1.9) размерность

этого условия. Она будет рав-

на 0

=1-1 •(2-1 + 1-1) = 2.

Таким образом, получаем

д7=а

(^;°о)+а.=4, что

говорит о корректности усло-

вий задачи. Основываясь на

теореме о проекции прямого

угла и соответствующих этой

Рис. 4.13. Модель перпендикулярности

прямой и плоскости

теореме построениях на графической модели (рис. 4.12), можно пред-

100

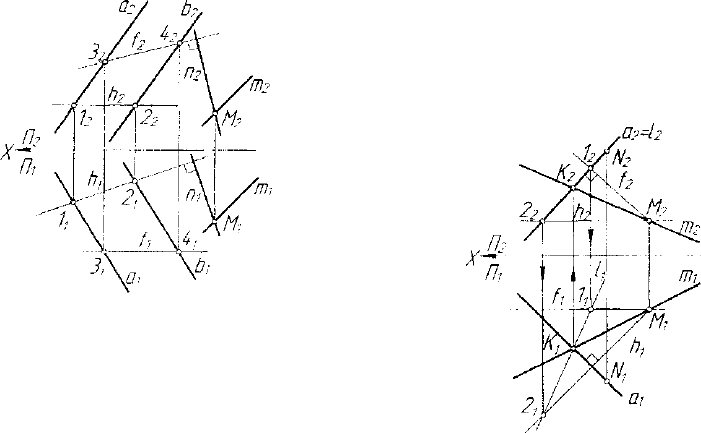
можно провести плоскость, перпендикулярную заданной. Для этого

необходимо лишь, чтобы эта плоскость проходила через перпендику-

ляр. Но через указанный перпендикуляр к данной плоскость проходит

пучок плоскостей, каждая из которых по признаку перпендикулярно-

сти будет перпендикулярна данной плоскости. Следовательно, выше-

приведенный признак перпендикулярности не определяет единствен-

ную плоскость, перпендикулярную данной. В этом проявляется след-

ствие отмеченной выше полуперпендикулярности. Для построения

единственной плоскости, перпендикулярной данной, необходимы до-

полнительные геометрические усло-

вия. Рассмотрим пример. Пусть на

графической модели заданы плос-

кость общего положения А{а//Ь)

и прямая т вне этой плоскости

(рис. 4.15). Требуется построить

плоскость £ и по следующим усло-

виям: Езт, £±Д. Выполним ана-

лиз исходных данных задачи. Пара-

метрическое число плоскости про-

странства Е

равно D'" =3. Условие

прохождения плоскости через пря-

мую можно символически выразить

. 2,1,0

как ?зу

. Размерность этого условия

по формуле (1.4) определяется сле-

дующим образом: Q

lj6

;{'o) =

Рис. 4.15. Модель построения

плоскости j 1ерпендикулярной

заданной плоскости

0ч

_(2-3-2)-(2 + 1)

-(3 + 1 + 0) = 2. Усло-

вие перпендикулярности двух плоскостей в пространстве Е

можно

символически выразить в виде е

•2,1,0

3,2,0 •

Размерность этого условия по

формуле (1.9) равна: Q

=^-2-(2-2 + ^2) = 1. В итоге получаем

тождественное равенство: D™ =

o(4'a,1)

Qx. ~ 3 • Следовательно,

условия задачи корректны и определяют единственную искомую

плоскость. На основании вышеизложенного может быть предложен

следующий алгоритм конструктивного решения рассматриваемой за-

дачи:

1. /1сА:/г

(1,,2

)//1; А, -> /г, = (1,,2]);

102

/сДЭДЛу/Л';

f,-*/

=(3

);

3. и

еи

,¥, em

;

4. «| ± А,, М, е М, е ли,.

Плоскость il(m г\ п) является искомой. При этом Мет- любая

точка прямой т; h и / - линии уровня в плоскости Д.

4.7. Проекции прямого угла, принадлежащего

плоскости общего положения

Рассмотрим на графической модели конструктивное решение за-

дачи о построении прямого угла, расположенного в плоскости общего

положения. Пусть заданы прямая общего положения а(а,,я

) и точка

М(М

,М

)<£а (рис. 4.16). Требуется построить прямую т по усло-

виям: М е т, т J_ a, mf]a . Очевидно,

все множество прямых, проходящих че-

рез точку М и перпендикулярных пря-

мой а, образует плоскость Д такую, что

М е Д, Д J. а. Очевидно также, что ис-

комая прямая т определится двумя

точками: М и К = af] Д. Проведем па-

раметрический анализ условий рассмат-

риваемой задачи. Как было показано ра-

нее, например, в пункте 1.1, параметри-

ческое число прямой линии пространст-

ва Е

равно = 4. Размерность усло-

вия прохождения прямой через точку

пространства равна Q

e(e\^) = 2. Раз-

мерность условия перпендикулярности

прямой заданной прямой пространства

определится но формуле (1.9) следующим образом:

Q L = 1 • 1 • (1 -1 +1 • 1) = 1. Размерность условия пересечения двух пря-

мых в пространстве, выраженного символически

е\'°

определится по

формуле (1.4) таким образом:

йл(е

;

:?) =

£1г>)-а±11-

(

)

Рис. 4.16. Модель построения

прямого угла в плоскости

общего положения

103

Получаем тождественное равенство параметрического числа ис-

комой прямой и суммы размерностей условий:

Полученный результат говорит о корректности условий данной

задачи. Алгоритм решения рассматриваемой задачи, на основании

вышеизложенного, может иметь следующий вид:

1. А : //X, М

е А

; М

е h

;

2. fX

//X,M

±a

;

3. (hf]f)f]a = K(K

);

4. (K

,Mi) = m

, (K

) = m

Прямая m(m

) является решением задачи. Пункты 1 и 2 в

этом алгоритме соответствуют решению задачи о перпендикулярно-

сти прямой и плоскости (п. 4.5). Пункт 3 алгоритма соответствует ре-

шению задачи о пересечении прямой и плоскости и его алгоритм был

рассмотрен ранее (п. 4.1). Таким образом, в соответствии с данным

алгоритмом, на графической модели построены проекции ZM

прямого угла ZMKN в плоскости общею положения

(af]m).

4.8. Частные случаи пересечений прямых, плоскостей

и гиперплоскостей пространства Е

В соответствии с теоремой о пересечении линейных подпро-

странств для пространства Е

можно составить следующую таблицу

пересечений (табл. 4.1):

Табл. 4.1

прямая плоскость

гиперплоскость

прямая

точка

плоскость

точка

прямая

гиперплоскость

точка прямая

плоскость

Частными случаями расположения линейных подпространств бу-

дут те, в которых оба пересекающихся подпространства являются

перпендикулярными плоскостям и гиперплоскостям проекций или

одно из двух пересекающихся подпространств является перпендику-

лярным плоскостям и гиперплоскостям проекций.

104

4.8.1. Пересечение проецирующих подпространств

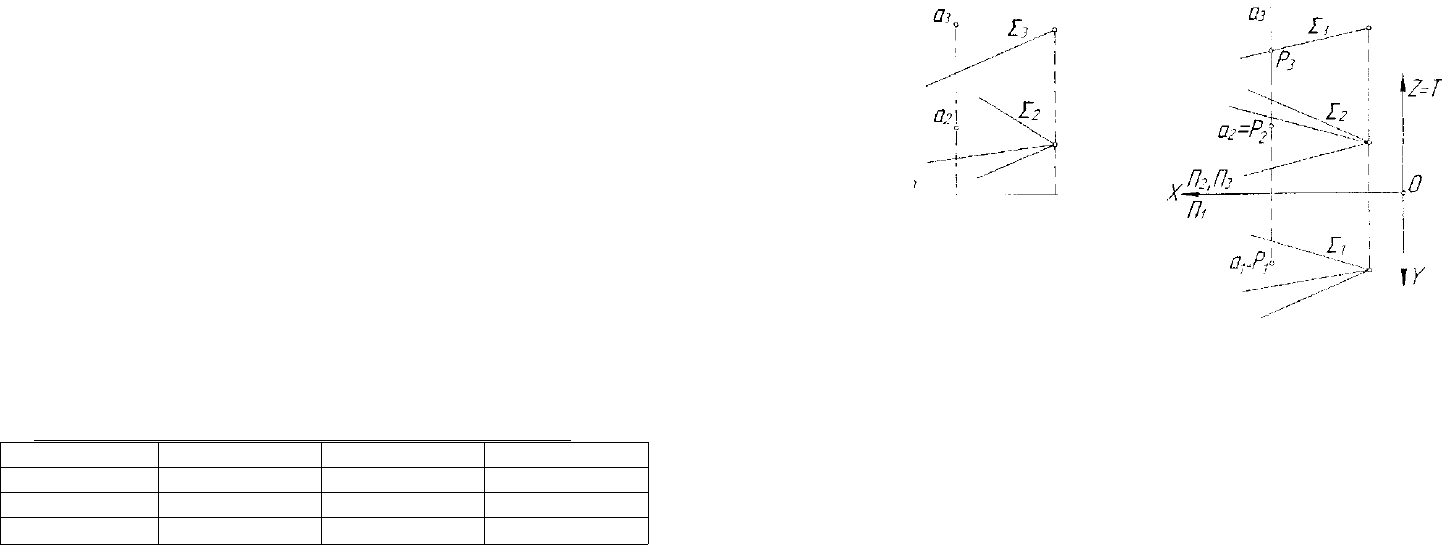
1. Прямая и гиперплоскость проецирующие.

Очевидно, что если прямая будет проецирующей относительно

какой-либо гиперплоскости проекций, а гиперплоскость будет про-

ецирующей относительно какой-либо плоскости проекций этой же

гиперплоскости проекций, то они будут параллельны. На рисунке 4.17

изображена прямая а 1 OXZT и гиперплоскость 27 ± ОХТ. Следова-

тельно, аIIOY и 2 1 OYZ. Следовательно, allЕ.

Z=T

-О

Г/

Рис. 4.17. Параллельные

проецирующие прямая а

и гиперплоскость 2

Рис. 4.18. Модель построения

пересечения проецирующих

прямой а и гиперплоскости 2

Вели прямая будет проецирующей относительно какой-либо ги-

перплоскости проекций, а гиперплоскость - относительно плоскости

проекций, не лежащей в этой гиперплоскости проекций, то их точка

пересечения определяется без дополнительных построений. На ри-

сунке 4.18 Р = а[\Е , а 1 OXYZ, 2 1 ОХТ.

Для сокращения построений на последующих рисунках не будем

указывать оси проекций X, Y, Z, Т на многомерных евклидовых

чертежах.

2. Плоскость и гиперплоскость проецирующие.

105

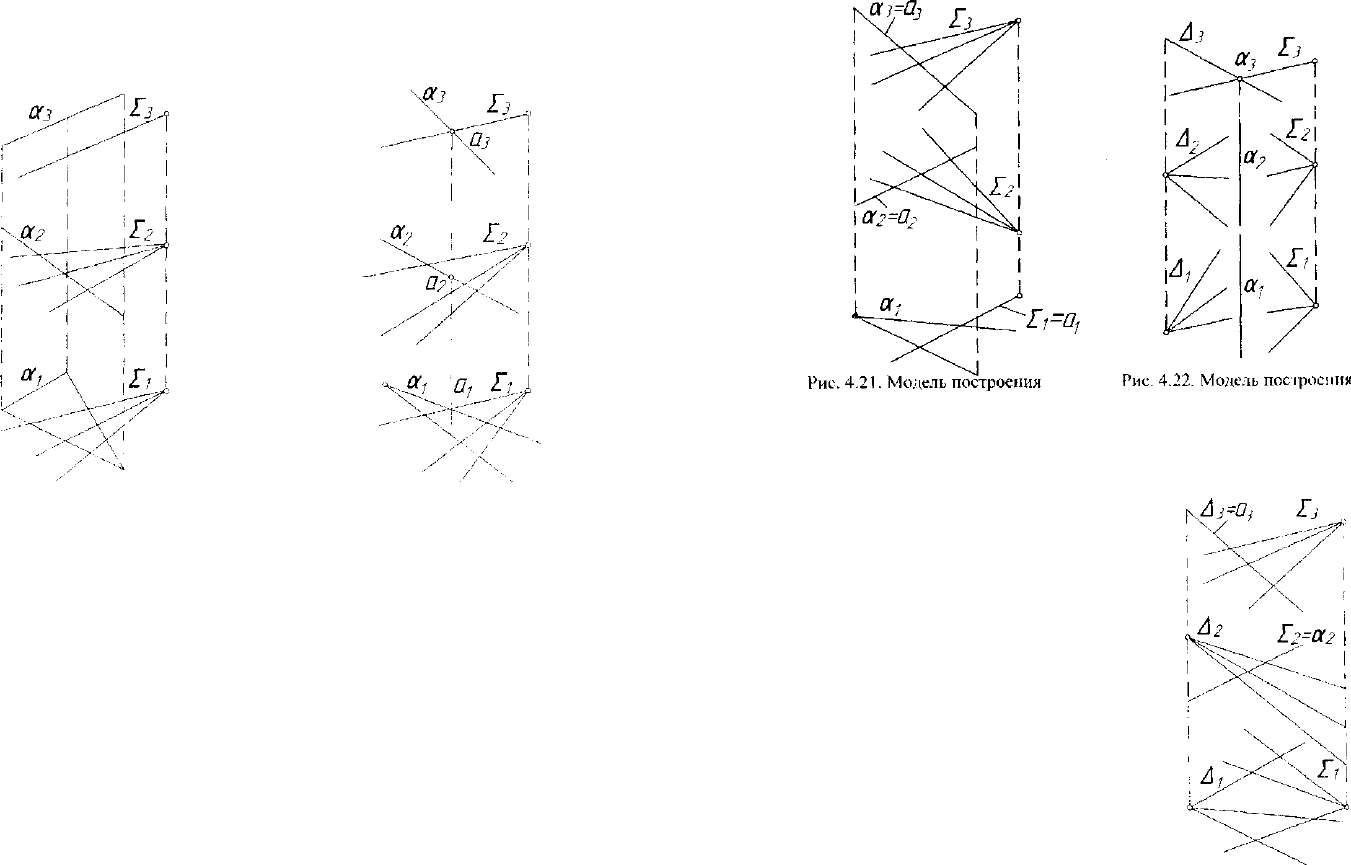
Случай, когда плоскость и гиперплоскость проецирующие отно-

сительно одной и той же плоскости проекций изображен на рисунке

4.19, где а 1 OXZT, Г1 ОХТ, а

II27

. Следовательно, all Е.

Рис. 4.19. Параллельные Рис. 4.20. Модель построения

проецирующие плоскость а пересечения проецирующих

и гиперплоскость 27 плоскости а и гиперплоскости 27

Если плоскость и гиперплоскость проецирующие относительно

одной и той же плоскости проекций, но а Н~21, то прямая их пересе-

чения определяется без дополнительных построений. На рисунке 4.20

а ± OXZT, XI OXZ.

Если плоскость и гиперплоскость проецирующие относительно

разных плоскостей проекций, то прямая их пересечения определяется

без дополнительных построений. На рисунке 4.21 a-LOXZT,

IIOXY, a = af\l'.

106

пересечения проецирующих пересечения проецирующих

плоскости а и гиперплоскости 27 гиперплоскостей J и 27

3. Гиперплоскости проецирую-

щие.

Пусть 27 и А - гиперплоскости,

проецирующие относительно одной

и той же плоскости проекций,

27 1 ОХТ, А 1 ОХТ. Тогда их плос-

кость а пересечения тоже перпен-

дикулярна ОХТ. Ее проекции опре-

деляются без построений (рис. 4.22).

Если гиперплоскости 27 и А

проецирующие относительно разных

плоскостей проекций, то их плос-

кость пересечения а определяется

без дополнительных построений

(рис. 4.23).

Рис. 4.23. Модель построения

пересечения проецирующих

гиперплоскостей А и 27

107

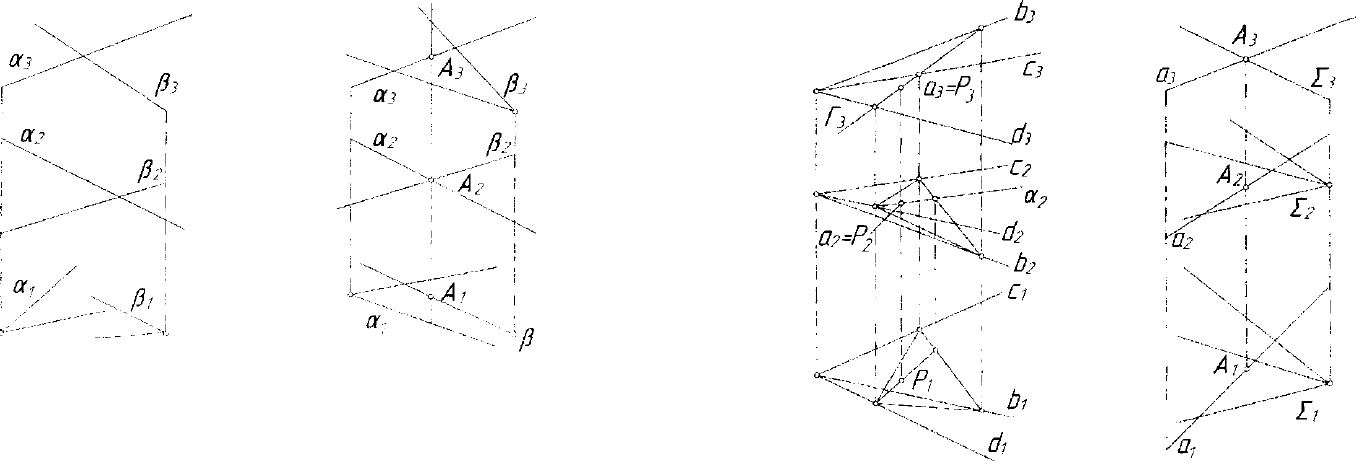
4. Плоскости проецирующие.

Нсли обе плоскости проецирующие относительно одной и той же

гиперплоскости проекций, то они пересекаются в точке, которая ле-

жит на оси координат, перпендикулярной этой гиперплоскости про-

екций. На рисунке 4.24 а 1 OXZT, В ± OXZT ,аГ]В=А

е OY.

Рис. 4.24. Модель пересечения

проецирующих плоскостей а и В

Рис. 4.25. Модель построения

пересечения проецирующих

плоскостей а и В

На рисунке 4.25 a J_ OXZT, В L OXYZ . Их точка пересечения А

лежит в плоскости, параллельной плоскости проекций OYT.

4.8.2. Пересечение подпространств,

одно из которых проецирующее

1. Прямая проецирующая, гиперплоскость общего положения.

Пусть заданы прямая a L OXZT и гиперплоскость E(b,c,d)

(рис. 4.26). В этом случае две проекции точки Р = af]Z уже готовые.

Это Р

а Р

. Чтобы найти проекцию Р

, через прямую а можно про-

вести проецирующую гиперплоскость Г(Г

) и найти плоскость ее

пересечения с 2". Затем в гиперплоскости Г провести плоскость

108

а(а

) и найти ее прямую пересечения с Г. Пересечение этой прямой

с а

есть проекция Р

2. Прямая общего положения, гиперплоскость проецирующая.

В этом случае точка A- af\Z, 2"(27

) определена без дополни-

тельных построений (рис. 4.27).

Рис. 4.26. Модель построения Рис. 4.27. Модель построения

пересечения проецирующих пересечения прямой общего

прямой а и гиперплоскости 27 положения а и проецирующей

общего положения гиперплоскости 27

3. Одна плоскость общего положения, вторая проецирующая.

Через проецирующую плоскость В проведена проецирующая

гиперплоскость Г(Г

) и построена прямая ее пересечения с « (рис.

4.28). Поскольку две прямые и плоскость В лежат в одной гиперпло-

скости Г, то они пересекаются в точке А = af] В, которая и есть ис-

комая.

4. Плоскость общего положения, гиперплоскость проецирую-

щая.

109

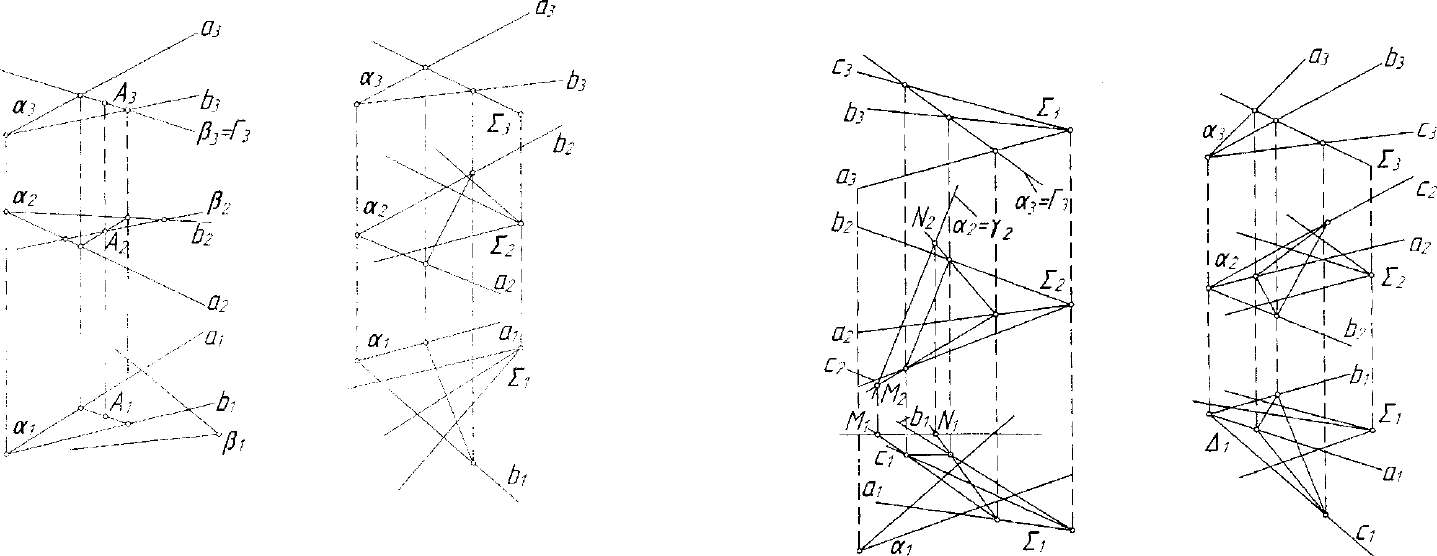
В этом случае одна из проекций прямой пересечения уже есть. На

рисунке 4.29 эта проекция совпадает с проекцией 27

гиперплоскости

27. Остальные проекции строятся по точкам пересечения с прямыми

а и b плоскости а(а, Ъ).

Рис. 4.28. Модель построения Рис. 4.29. Модель построения

пересечения плоскости общего пересечения проецирующей гинер-

иоложения а и проецирующей плоскости 27 и плоскости общего

плоскости В положения а

5. Плоскость проецирующая, гиперплоскость общего положе-

ния.

В этом случае через плоскость а проводится проецирующая ги-

перплоскость Г(Г

) (рис. 4.30), а

= Г

. По трем точкам пересечения

с прямыми a, b и с строится плоскость пересечения Г и Z(a,b,c).

Через плоскость а проводится плоскость у(у

), &г~Уг> У

• По

точкам М и N строится прямая MN = аС\£.

6. Одна гиперплоскость проецирующая, вторая общего поло-

жения.

Построение плоскости пересечения гиперплоскостей 27(27

) и

А(а, /3, с) приведено на рисунке 4.31.

Рис. 4.30. Модель построения Рис. 4.31. Модель построения

пересечения проецирующей пересечения гиперплоскостей

плоскости и гиперплоскости общего положения А и

общего положения проецирующей 27

ill

но

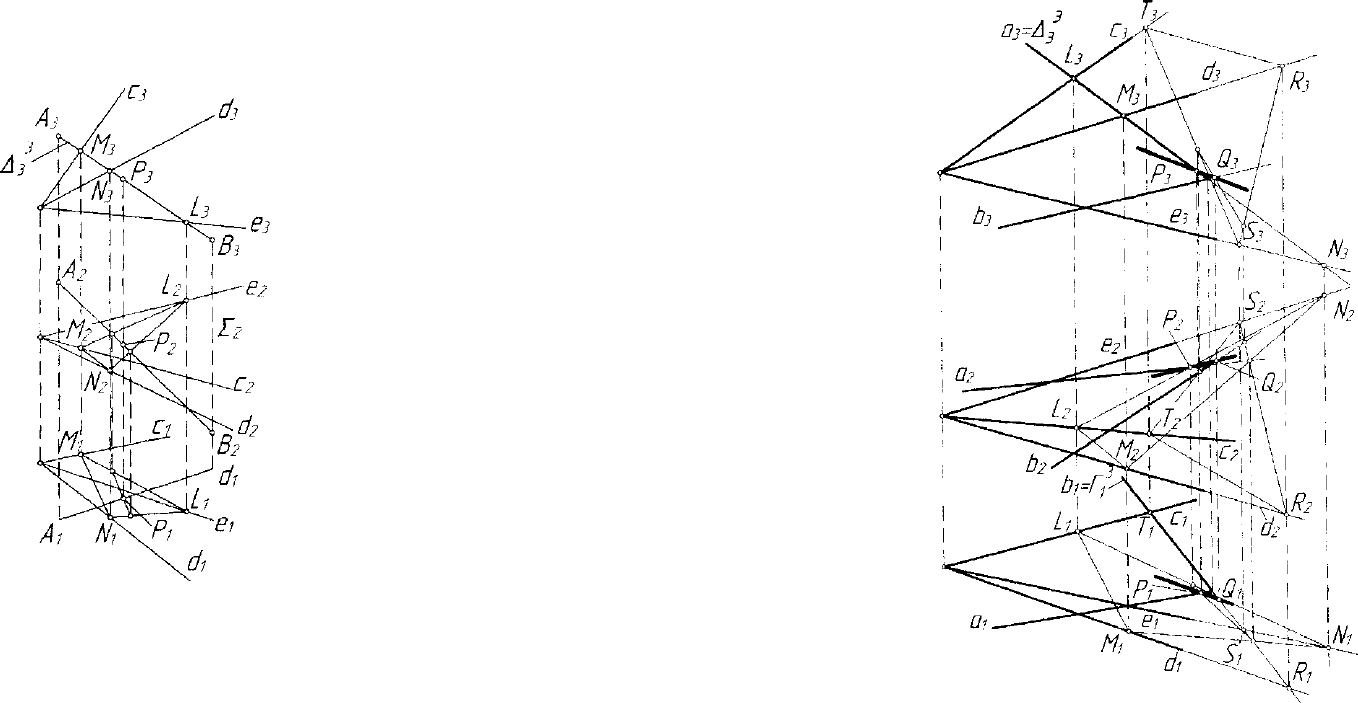
4.9. Общие случаи пересечения подпространств

пространства Е

4.9.1. Пересечение прямой и гиперплоскости

В соответствии с теоремой о пересечении линейных подпро-

странств имеем для пространства Е

: 3 + 1-4 = 0, т.е. пересечением

прямой и гиперплоскости является точка. Если эта точка несобствен-

ная, то прямая и гиперплоскость параллельны.

Рассмотрим конструктивный

алгоритм построения точки пересе-

чения прямой А В общего положе-

ния и гиперплоскости 27, заданной

тремя прямыми с, d, е, пересе-

кающимися в одной точке (рис.

4.32).

Можно рассуждать так: в ги-

перплоскости (c\d,e) выбирается

2 плоскость А

, конкурирующая с

прямой А В относительно какой-

либо плоскости проекций. Можно

через прямую АВ провести проеци-

рующую гиперплоскость А

относи-

тельно какой-либо плоскости про-

екций. Оба эти действия равносиль-

ны. На чертеже проводится плос-

кость Д

или гиперплоскость А\.

Пересечением А

и 27 является

2-плоскость (L,M,N). Теперь пря-

мая АВ и 2-плоскость (L,M,N)

лежат в одной гиперплоскости А" и

моделируются двумя проекциями

А,В„ А

и (LpA/piV,), (L

). Дальнейшее решение задачи

совпадает с алгоритмом, описанным в п. 4.8.1. Результатом является

точка Р = ABf] 27.

Рис. 4.32. Модель пересечения

прямой (АВ) и гиперплоскости

(с, d, е) общих положений

112

4.9.2. Пересечение плоскости и гиперплоскости

Пересечение плоскости и гиперплоскости является прямая, но-

жольку 2 + 3-4 = 1. Для ее построения необходимо дважды приме-

тить алгоритм построения точки пересечения прямой и гипсрплоско-

:ти, а в качестве двух прямых будут любые две прямые заданной

тлоскости.

Рис. 4.33. Модель построения пересечения плоскости (а,Ь)

и гиперплоскости (с, d. е) общих положений

из

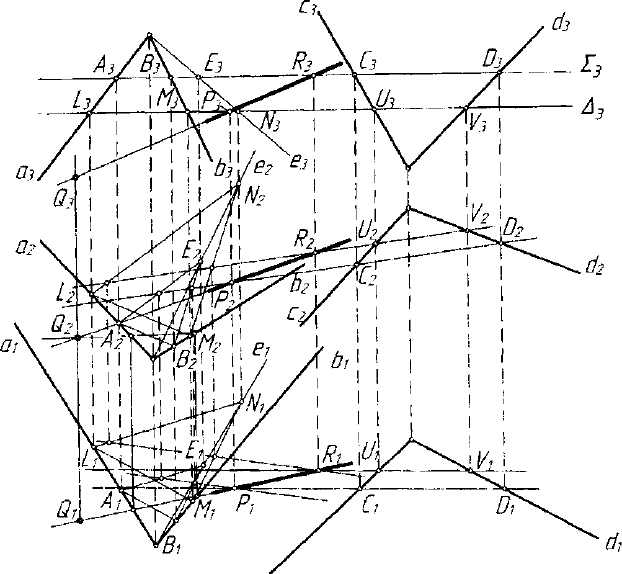
Пусть плоскость задана двумя пересекающимися прямыми а,Ь, а

гиперплоскость - тремя c,d,e, пересекающимися в одной точке (рис.

4.33). Через прямую а проведена проецирующая гиперплоскость А\;

построена плоскость (L,M ,N)= A

f](c,d,e) и найдена точка

р = ap\{c,d,e). Затем через прямую Ъ проведена проецирующая ги-

перплоскость Г

; построена плоскость (R,S,T)= r^f](c,d,e) и най-

дена точка Q - ЬГ] (с, d, е). Искомая прямая PQ есть прямая пересече-

ния заданной гиперплоскости (c,d,e) и плоскости (а,Ь).

4.9.3. Пересечение двух плоскостей

Две плоскости общего положения пространства Е

пересекаются

в точке, поскольку 2 + 2-4 = 0. Для ее построения необходимо одну

из заданных плоскостей заключить в гиперплоскость; построить пря-

мую пересечения второй плоскости и этой гиперплоскости; построить

точку пересечения первой плоскости и построенной прямой.

Пусть первая плоскость задана двумя пересекающимися прямы-

ми а,Ь, вторая - прямыми c,d (рис. 4.34). Заключим плоскость (а.Ь)

в произвольную гиперплоскость, для чего проведем через точку пере-

сечения прямых а и b произвольную прямую с. Для того, чтобы

найти прямую пересечения гиперплоскости (а,Ь,е) и 2—плоскости

(c,d) выберем две проецирующие гиперплоскости 27(27,) и Л(А-А.

Тогда получим: Щ(а,Ь,е) = (А,В,Е), АГ\ (а. Ь, е) = (/7, Л/, Л'),

27Г) (с, d) = (С, D), ЛГ| (с, d) = (U, V).

Снова применим принцип понижения размерности пространства,

т.е. все построения в проекциях на /7, и Я

(Я, =ОХУ',П

= OXZ)

моделируют пространственные построения в гиперплоскостях Е и А.

Заметим, что выбор 27(27

) и Л(Л

) произволен, они не обязательно

должны быть параллельными.

Найдены точки Р = (С, D)f](А,В,Е) и R = UVC\(L,M,N). Пря-

мая (Р,R)есть прямая пересечения гиперплоскости (а,Ь,е) и плос-

кость (c.d).

114

Рис. 4.34. Модель построения пересечения двух плоскостей (а,Ь) и (c,d)

общих положений

Теперь используя только проекции на П

и П

строится точка

Q = (P,R)C\(a,b), которая и есть искомая точка пересечения

Q = (a,b)r\(c,d).

4.9.4. Пересечение двух гиперплоскостей

Если даны две гиперплоскости 27 и А общего положения, то их

пересечением является плоскость общего положения. Построить ее

можно следующими двумя способами:

115

а) в одной из данных гиперплоскостей выбрать три прямые и

найти их точки пересечения со второй гиперплоскостью (т.е. трижды

повторить алгоритм в п. 4.9.1). Три несобственные точки зададут ис-

комую плоскость;

б) выбрать две проецирующие гиперплоскости и найти их пере-

сечение с каждой из заданных гиперплоскостей. Затем найти прямые

пересечения двух плоскостей, лежащих в этих проецирующих гипер-

плоскостях. Результатом будут две пересекающиеся прямые, задаю-

щую плоскость пересечения заданных гиперплоскостей.

Первый способ приведен на рисунке 4.32, второй - на ри-

сунке 4.34.

4.10. Перпендикулярность линейных подпространств

пространства £

Сформулируем признаки перпендикулярности двух линейных

подпространств пространства Е

1. Прямая перпендикулярная гиперплоскости, если она перпен-

дикулярна прем, пересекающимся в одной точке, прямым этой гипер-

плоскости.

Этот же признак можно сформулировать иначе: прямая перпен-

дикулярна гиперплоскости, если она перпендикулярна любым двум

скрещивающимся прямым этой гиперплоскости. Или: прямая перпен-

дикулярна гиперплоскости, если она перпендикулярна двум пересе-

кающимся плоскостям этой гиперплоскости

2. Плоскость перпендикулярна гиперплоскости, если она прохо-

дит через перпендикуляр к этой гиперплоскости.

3. Две гиперплоскости перпендикулярны, если одна из них про-

ходит через перпендикуляр к другой.

4. Две плоскости перпендикулярны, если каждая из двух пересе-

кающихся прямых одной плоскости перпендикулярна двум пересе-

кающимся прямым другой плоскости.

5. Две плоскости полуперпендикулярны, если одна из них про-

ходит через перпендикуляр к другой.

В общем случае, когда линейные образы (прямые, плоскости, 3-

плоскости, ...) заданы в общем положении, по модели, не пользуясь

никакими дополнительными построениями, невозможно определить

перпендикулярны они друг другу или нет. Однако в частных случаях

это возможно. Если знать частные случаи, т.е. знать признаки перпен-

П6

днкулярности линейных образов на чертеже (на модели), можно пу-

тем преобразований привести их к виду, удобному для применения

признаков перпендикулярности. Эти признаки являются обобщением

известных признаков перпендикулярности прямых и плоскостей на

модели Монжа пространства Е

. А именно:

- две прямые перпендикулярны, если одна пара их одноименных

проекций перпендикулярна, а из другой пары одна из проекций па-

раллельна оси этих проекций;

- прямая перпендикулярна плоскости, если проекции линий

уровня данной плоскости перпендикулярны одноименным проекциям

данной прямой.

Обобщением этих признаков на модель пространства Е

являют-

ся следующие.

1. Две прямые перпендикулярны, если одна пара их одноимен-

ных проекций перпендикулярна, а в двух других парах одна из проек-

ций (одна и та же) параллельна оси этих проекций.

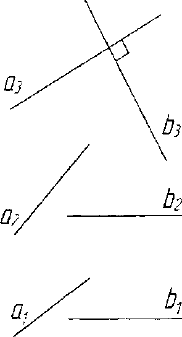
На рисунке 4.35 изображены две

перпендикулярные прямые а и А. В

силу того, что проекции /3, и Ь

парал-

лельны оси проекций и а

L Ь

, поло-

жение проекций я, и а

значения не

имеет, т.е. они могут быть любыми.

Проекцию а

можно считать сле-

дом а

гиперплоскости а. Тогда

b La и, следовательно, b перпенди-

кулярна любой прямой а с: а. Но в

этом случае b перпендикулярна и лю-

бой плоскости гиперплоскости а. По-

этому а

можно считать вырожденной

проекцией плоскости 27(Г

=а

), Рис. 4.35. Модель двух

у (~

Ъ LZ перпендикулярных прямых

2. Прямая перпендикулярна гиперплоскости, если проекции

данной прямой перпендикулярны одноименным проекциям линий

уровня данной гиперплоскости.

На рисунке 4.36 изображена прямая а, перпендикулярная гипер-

плоскости a(b,c,d), заданной своими прямыми уровня.

117

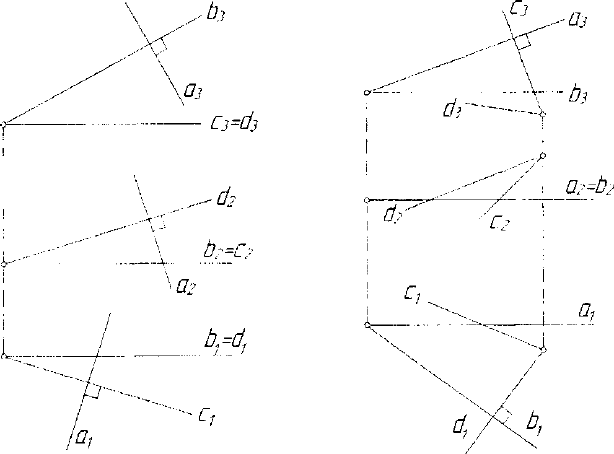
Естественно, что прямая а будет перпендикулярна любой плос-

кости Е с; a(b,c,d), например, плоскости E(b,d).

3. Две плоскости перпендикулярны, если две прямые одной

плоскости перпендикулярны, соответственно, двум линиям уровня

второй плоскости.

На рисунке 4.37 изображена плоскость Е(а,Ь), заданная своими

линиями уровня а(а

,а

) и bib

) и перпендикулярная ей

плоскость A{c,d), с La, d Lb.

Рис. 4.36. Модель прямой, Рис. 4.37. Модель перпендикулярных

перпендикулярной гиперплоскости. плоскостей Е(а,Ь) и A(c,d).

118

ГЛАВА 5. КРИВЫЕ ЛИНИИ

Начертательная геометрия изучает модели объектов пространст-

ва, в частности, евклидова трехмерного Е

, на плоскости. В предше-

ствующих главах были рассмотрены модели линейных объектов

(элементов) евклидова пространства, а именно: точки, прямой линии,

плоскости, а также задачи позиционного, аффинного и метрического

характера с участием этих объектов. Кроме линейных, в пространстве

существуют и нелинейные объекты, к которым относятся кривые ли-

нии, поверхности и множества этих объектов. Нелинейные объекты

обладают рядом, специфических для каждого из них, геометрических

свойств, которые отсутствуют у линейных объектов, например, нали-

чие кривизны. Процесс моделирования на плоскости нелинейного

объекта включает последовательное выполнение следующих этапов:

1. Получение определенного значного соответствия, модели-

рующего поверхность, а в случае моделирования линии — получение

определенных точечных подмножеств (образа и прообраза), соответ-

ственных в некотором соответствии.

2. Установление взаимосвязи (соответствия) геометрических

свойств нелинейного объекта пространства и геометрических свойств

его модели.

Целью второго этапа является достижение достаточно полного

представления о том, как и во что при моделировании отображаются

геометрические свойства объекта, и каким образом можно восстано-

вить геометрические свойства объекта по его модели. Выполнение

лишь первого этапа, которым на протяжении своей истории занима-

лась начертательная геометрия, изучая различные аппараты проеци-

рующего отображения пространства на плоскость, нельзя признать в

качестве полного моделирования нелинейного объекта пространства.

Для выполнения второго этапа необходимы, во-первых, знания гео-

метрических свойств объектов, в том числе в малом (в бесконечно

малой окрестности точки); во-вторых, знания геометрических свойств

в малом самого отображения (при конструктивном моделировании

речь идет о проецирующем отображении). В свете сказанного оче-

видна актуальность проблемы полного моделирования нелинейных

объектов евклидова пространства. В настоящее время решение этой

проблемы находится в начальной стадии и требует привлечения зна-

ний из областей других геометрий: проективной, аналитической, ал-

гебраической, исчислительной, дифференциальной и др.

119