Волков В.Я. и др. Курс начертательной геометрии на основе геометрического моделирования
Подождите немного. Документ загружается.

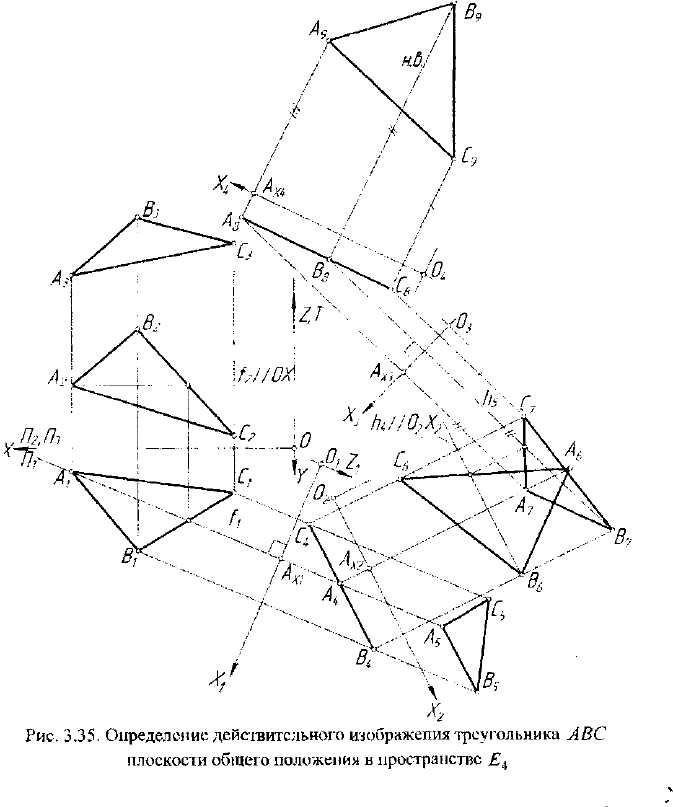
3.5.2. Определение действительного
изображения треугольника ABC
Определение действительного изображения треугольника ABC -
это задача по преобразованию плоскости общего положения ABC в
частное положение.
Пусть задана плоскость ABC общего положения. Это означает,
что, например, h
3
II ОХ , h,J ОХ , h
x
HOX или /
3
# ОХ , /
2
//ОХ ,
/, i ОХ или q
3
# ОХ , q
2
# ОХ, q
x
ll ОХ • Выберем любую из этих ли-
ний уровня. На рисунке 3.35 выбрана линия /
2
// ОХ и построена /,.
Можно было построить /
3
и вести все построения относительно нее.
Выбрана новая гиперплоскость проекций o
x
X
x
ZT , при этом ось ОХ,
принадлежит плоскости OXY . На гиперплоскости проекций построе-
ны проекции Л
4
£
4
С
4
и А
5
В
5
С
5
, причем А.
Х
В
Л
С,
Х
- вырожденная про-
екция.
Затем выбрана гиперплоскость проекций 0
2
X
2
ZT , параллельная
плоскости
ЛВС. На
чертеже это означает- выбор оси
О
г
Х
2
//
Л
4
Я
4
С
4
.
Построены проекции А
Л
В
6
С
в
и Л
7
В
7
С-,. Поскольку ABC И ()
2
Х
2
ZT , то
на эту гиперплоскость треугольник ABC проецируется в "натураль-
ную величину". Другими словами, плоскость ЛВС в системе
0
2
X
2
YZT является плоскостью уровня. Таким образом, произошло
понижение размерности пространства, в котором расположена плос-
кость ABC. Теперь можно считать, что треугольник ABC расположен
в трехмерном пространстве и его проекции есть А
6
В
Ь
С
Ь
и Л
7
#
7
С
7
.
Дальнейшие построения такие же, как и в трехмерном пространстве.
Окончательно получаем проекцию A
9
B
q
C
q
, которая представляет со-
бой действительное изображение треугольника ABC.
В зависимости от выбора прямой уровня можно реализовать
шесть направлений решения задачи. Во всех из них будет получено
одно и то же действительное изображение треугольника ABC.
На
рисунке
3.35
выбор осей
О
х
Х
х
, О
г
Х
2
, 0
3
Х
3
, 0,Х_
Х
диктует-
ся направлением линий /,, Л
4
В
4
С
4
, А
5
, Л
8
#
8
С
8
. Расстояния, отклады-
ваемые
от
осей
O
i
X
i
следующие:
l-^^nj
=
ИгЛт!'
j^s^xi!
=
ИзДг|>
= |.4
7
4гз|. Аналогично, для точек В
х
...., В
9
и С,,..., С
9
.
80
81
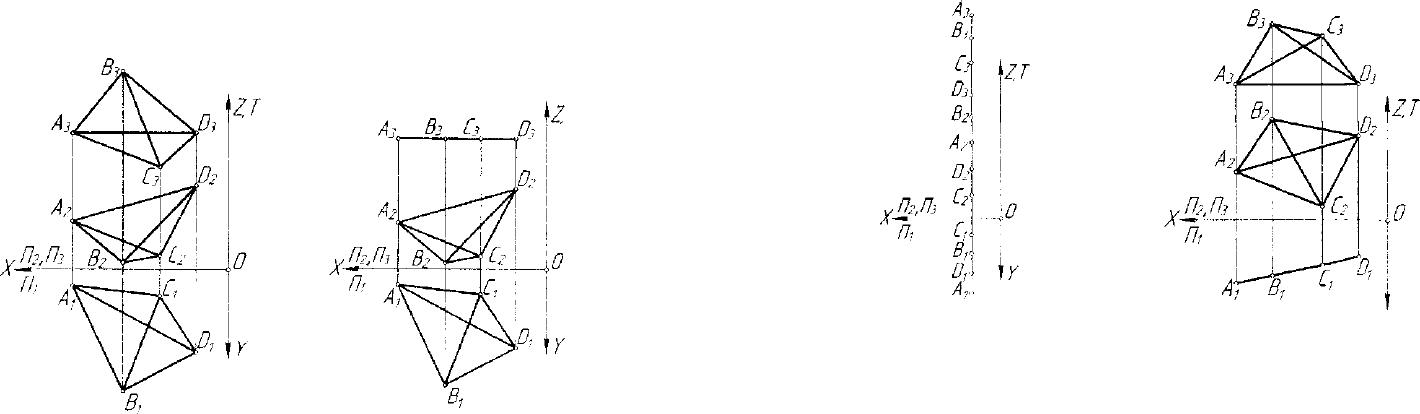
3.6. Моделирование гиперплоскостей пространства Е
п
Гиперплоскость (3-плоскость) пространства Е
п
определяется че-
тырьмя параметрами или задается четырьмя независимыми точками
пространства. Пусть это будут точки A,B,C,D . Тогда на простейшей
модели будут проекции (A
U
A
2
,A
2
), (S,,B
2
, В
3
), (С
15
С
2
,С
3
) и
(£>,.D
2
,£>
3
) (рис. 3.36). От этого задания можно перейти к другому
заданию гиперплоскости, например, двумя скрещивающимися пря-
мыми - ребрами тетраэдра ABCD , плоскостью и точкой - гранью и
противоположной вершиной тетраэдра ABCD , плоскостью и пересе-
кающей ее прямой, тремя прямыми, пересекающимися в одной точке
и т.д.
Судя по чертежу, можно утверждать, что гиперплоскость ABCD
является гиперплоскостью общего положения по отношению к гипер-
плоскостям проекций OXYZ , OXYT , OXZT , но ничего определенно-
го нельзя сказать о ее положении относительно гиперплоскости
OYZT .
Гиперплоскость ABCD частного положения может быть парал-
лельна одной из гиперплоскостей проекций. Например, если
Рис. 3.37. Гиперплоскость уровня
относительно гиперплоскости
OXYZ пространства Е
4
Рис. 3.36. Модель гиперплоскости
пространства Е
л
/
4
= t
B
= t
c
= t
D
= сош7 , то гиперплоскость ABCD будет параллельна
гиперплоскости OXYZ (рис. 3.37). Такая гиперплоскость называется
гиперплоскостью уровня.
На рисунке 3.38 приведена модель гиперплоскости уровня
(ABCD )// OYZT, для которой х
А
= х
в
= х
с
= x
D
= const.
Рис. 3.38. Гиперплоскость уровня Рис. 3.39. Проецирующая относительно
Гиперплоскость может быть перпендикулярна какой-либо плос-
кости проекций. Тогда на этой плоскости проекций проекция гиперп-
лоскости будет вырожденной. На рисунке 3.39 показана гиперпло-
скость ABCD , перпендикулярная плоскости OXY . Такая гиперпло-
скость называется проецирующей относительно плоскости OXY .
Аналогично будут выглядеть модели проецирующих гиперплоскостей
относительно других плоскостей проекций.
Следует заметить, что невырожденными проекциями гиперпло-
скости будут все поля проекций OXZ , OXY (рис. 3.37) и ОХТ, OXZ
(рис. 3.39).
3.6.1. Принадлежность точки, прямой и плоскости гиперплоскости
Можно сформулировать следующие признаки принадлежности:
Y
относительно гиперплоскости
OYZT пространства Е
А
OXY гиперплоскость
пространства
83
82
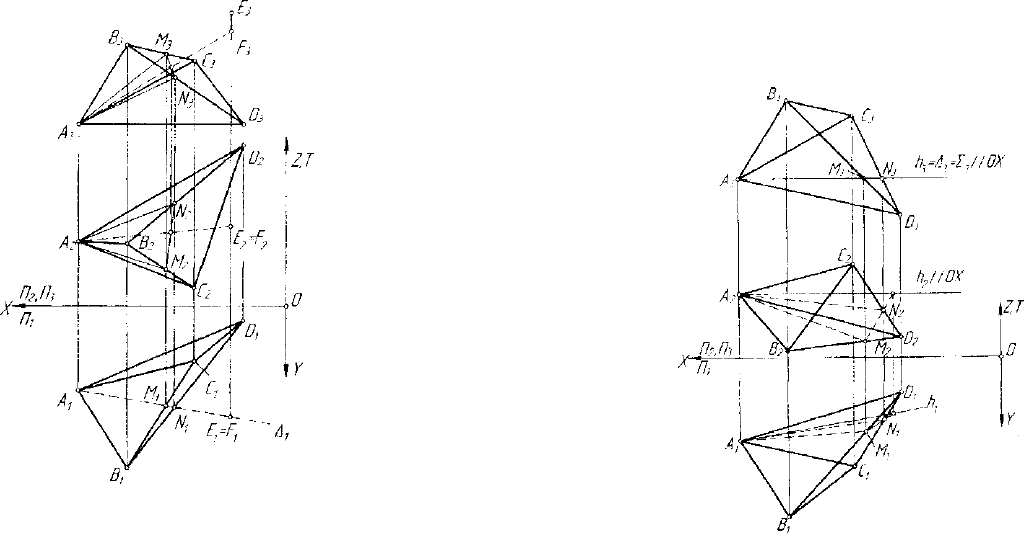
1) точка принадлежит гиперплоскости, если она принадлежит
какой-либо линии данной гиперплоскости;
2) точка принадлежит гиперплоскости, если она принадлежит
какой-либо плоскости данной гиперплоскости;
3) прямая принадлежит гиперплоскости, если две ее точки при-
надлежат данной гиперплоскости;
4) плоскость принадлежит гиперплоскости, если три ее точки, не
лежащие на одной прямой, принадлежат данной гиперплоскости.
Очевидно, что для рисунков 3.37, 3.38, 3.39 задача о принадлеж-
ности точки данной гиперплоскости частного положения решается
просто, без дополнительных построений. Так на рисунке 3.37 доста-
точно, чтобы проекция Е
3
точки Е(Е
}
,Е
2
,Е
3
) принадлежала пря-
мой A
3
B
3
C
3
D
3
. Тогда Е е (ABCD). То же самое относится к гиперп-
лоскости, изображенной на рисунке 3.39. Если E
]
sA
]
B,C
l
D
l
, то
Е(Е
Х
,Е
2
,Е
3
) е (ABCD ).
Рассмотрим эту задачу в
общем случае. Пусть дана ги-
перплоскость ABCD (рис. 3.40).
Пусть будет' дана точка
Е{Е,,Е
2
.Е
3
), относительно ко-
торой нельзя сказать ничего оп-
ределенного по принадлежности
ее данной гиперплоскости.
Предположим, что существует
точка F(F
}
,F
2
), принадлежащая
данной гиперплоскости и кон-
курирующая с Е относительно
плоскостей OXY и OXZ . Тогда
по условию принадлежности,
можно построить точку F, -
проекцию точки F на плос-
кость ОХТ. Если F
3
Е е (ABCD), если F
3
* £
Ег(ABCD).
Для реализации этой идеи
проведем через точку Е гипер-
плоскость А, перпендикулярную
Е
3
, то
то
Рис. 3.40. Принадлежность точки
гиперплоскости пространства £
4
84
плоскости OXY . Это можно сделать бесконечным числом способов.
На рисунке 3.40 гиперплоскость Л(4) проведена через точку А . Пе-
ресечение ABCD и А будет плоскость, которую можно построить по
трем точкам А, М, iV, где М е ВС, N е BD . Таким образом, полу-
чаем А
г
= (A
2
M
2
N
2
), А
ъ
= (/i
3
M
3
JV
3
). Очевидно, что размерность по-
нижена до трех, и мы получили задачу на принадлежность точки
E(E
]t
E
2
) плоскости A(A
2
M
2
N
2>
A
3
M
3
N
3
). Дальнейшее решение было
описано выше.
На рисунке 3.40 Е
3
* Е
3
, следовательно, Е е (ABCD).
Для решения задачи о принадлежности прямой и плоскости дан-
ной гиперплоскости необходимо описанный алгоритм повторить два
и три раза, соответственно.
3.6.2. Прямые уровня и плоскости уровня
в данной гиперплоскости
В данной гиперплоскости общего положения ABCD MOiyr быть
выбраны прямые, параллельные какой-либо гиперплоскости ироек-
Рис. 3.41. Прямая уровня гиперплоскости
относительно плоскости OXY пространства £
4
85
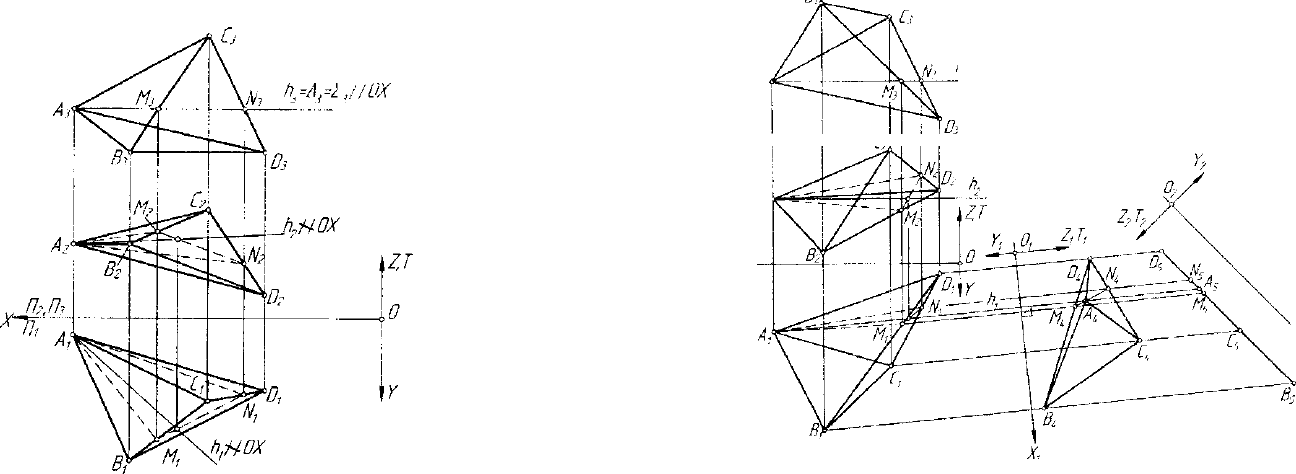
ций, и прямые, параллельные какой-либо плоскости проекций. На ри-
сунке 3.41 изображена прямая h(h„k
2
,h
3
) данной гиперплоскости,
параллельная плоскости OXY , а на рисунке 3.42 - прямая h(h
x
,h
2
,h
3
)
данной гиперплоскости, параллельная гиперплоскости OXYZ .
Для проведения прямой hllOXY предварительно проведена ги-
перплоскость уровня S(Z
3
)II OXYZ . Строить другие проекции ги-
перплоскости 27 нет необходимости. В гиперплоскости 27 выбрана
плоскость уровня A(A
3
)IIOXYZ, проекции A
2
(A
2
M
2
N
2
) и
A
X
(A
X
M
X
N
X
) строятся по точкам М и N, М GBD, N е CD . Гиперп-
лоскость 27 проведена через вершину А тетраэдра ABCD для эко-
номии построений. Проекции h
2
и h
x
прямой уровня h строятся по
условию принадлежности плоскости уровня А. При этом h
3
II ОХ ,
h
2
II OX ,h
x
iOX.
Построение прямой h, he (ABCD) и h II XYZ выполняется точно
так же, как и в предыдущем случае. Однако теперь в плоскость
A(AMN) можно выбрать любую прямую h(h
2
# ОХ) и построить иро-
Рис. 3.42. Прямая уровня гиперплоскости
относительно плоскости OXYZ пространства Е,
86
екцию Л, по принадлежности. Получаемая прямая h(h
u
h
2
,h
3
) будет
параллельна гиперплоскости OXYZ .
Если бы А, оказалась тоже параллельной оси ОХ, то это бы озна-
чало, что заданная гиперплоскость ABCD не является гиперплоско-
стью общего положения. В этом случае гиперплоскость ABCD была
бы перпендикулярна гиперплоскости OYZT или, что, то же самое,
была бы параллельна оси ОХ .
Очевидно, что в гиперплоскости ABCD общего положения
нельзя найти и построить плоскость, параллельную какой-либо плос-
кости проекций.
3.б.3. Преобразование гиперплоскости общего положения в
проецирующую гиперплоскость и гиперплоскость уровня
Для преобразования данной гиперплоскости общего положения в
гиперплоскость проецирующую относительно какой-либо гиперпло-
А_
А-/
х-
П?,П
3
\
\
*2
Рис. 3.43. Преобразование гиперплоскости общего положения
пространства Е
А
в проецирующую гиперплоскость
87
скости проекций необходимо в данной гиперплоскости построить
прямую уровня. На рисунке 3.43 выбрана прямая уровня А(А,, А,, А
3
),
параллельная плоскости OXY . Новая гиперплоскость проекций
OA'JZJT,
перпендикулярна прямой h, т.е. ± А,. В новой системе
проекций гиперплоскость ABCD является проецирующей относи-
тельно плоскости ОХ
Х
Т
Х
.
Если задать ось о
2
Х
г
параллельно вырожденной проекции
А
5
В
5
С
5
0
5
, то в новой системе проекций o
2
X
2
Y
2
Z
2
T
2
гиперплоскость
ABCD станет гиперплоскостью уровня относительно гиперплоскости
88
ГЛАВА 4. ВЗАИМНОЕ ПОЛОЖЕНИЕ
ЛИНЕЙНЫХ ПОДПРОСТРАНСТВ
В пространстве Е
3
прямая и плоскость, а также две плоскости,
могут пересекаться, быть параллельными или перпендикулярными.
Выполним на рассматриваемой графической модели решения пози-
ционных, аффинных и метрических задач для указанных пар геомет-
рических объектов.
4.1. Пересечение прямой и плоскости
Из аксиомы стереометрии [7]: «Если две точки прямой лежат в
плоскости, то все точки прямой лежат в плоскости» следует, что
прямая и плоскость могут пересекаться в точке - собственной или не-
собственной (бесконечно удаленной). В последнем случае прямая и
плоскость являются параллельными, кроме того, исходя из формулы
s = m + q-n размерности пространства пересечения (п. 1.7.2), также
получаем пересечение прямой и плоскости пространства Е
3
в точке,
поскольку 5 = 2 + 1- 3 = 0.
Рассмотрим алгоритм конструктивного определения точки пере-
сечения прямой и плоскости. Пусть на чертеже (рис. 4.1) заданы
плоскость Ф(а// в) и не принадлежащая ей прямая с(с
г
,с
2
). Требует-
ся определить точку пересечения сГ)Ф. Отметим, что существуют
различные решения данной задачи [23]. Наиболее простое графиче-
ское решение ее может быть выполнено на основе применения пары
конкурирующих прямых, принадлежащих одной проецирующей
плоскости. Одной прямой этой пары служит заданная прямая с, а
другой - прямая d с Ф. В этом случае определение искомой точки
пересечения с[}Ф сводится к определению точки пересечения cf]d,
поскольку при с Ф имеет место тождественное равенство
с(]Ф - cf]d. Алгоритм решения задачи может иметь нижеследующий
вид.
1. c
2
=d
2
(прямые с и d - фронтально-конкурирующие);
2. d
2
f)a
2
=1
2
, d
2
f]e
2
=2
2
;
3. 1
2
-И, еа,, 2
2
—>2
Х
ее,;
4. ri, =(lj,2]) - проекция d
x
прямой d определена проекциями
l|,2j ее точек 1 и 2;
89
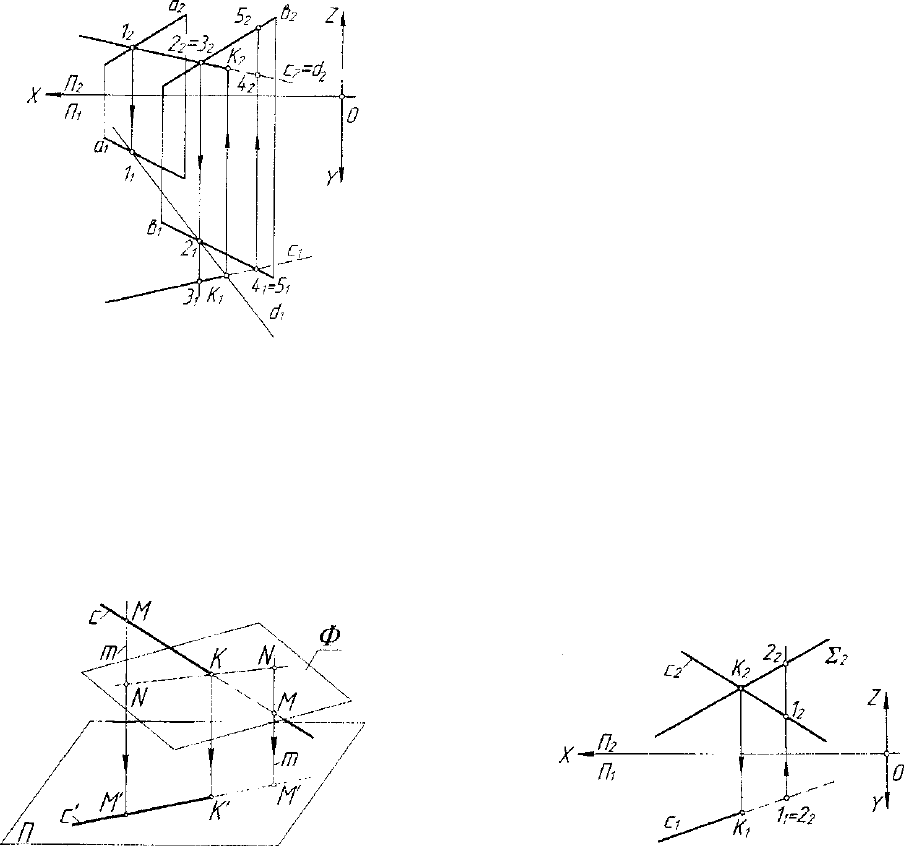
5.
Точка
Рис. 4.1. Модель построения
пересечения прямой и плоскости
К(К
Х
, К
2
) является решением
задачи.
Для полноты представле-
ния расположения прямой с и
плоскости Ф относительно
друг друга и относительно
плоскостей проекций Я, и П
2
необходимо рассмотреть оп-
ределение видимости прямой
с при ее пересечении с плос-
костью Ф. Видимость опре-
деляется относительно плос-
кости проекции с учетом на-
правления проецирования.
Смысл сказанного и способ
определения видимости заключается в следующем. Предположим,
что заданы: плоскость ортогонатьных проекций 77, прямая с и плос-
кость Ф с их точкой пересечения К (рис. 4.2). Очевидно, последняя
является границей видимости прямой с относительно плоскости Ф
при проецировании на П. Возьмем на прямой с точку М * К и про-
ведем проецирующую прямую т 1 П такую, что Mem. 11усть
тГ\Ф-А', тГ\П = М'. Тогда на прямой т возможны расположения
тройки точек в последова-
тельности, соответствую-
щей ортогональному про-
ецированию на 77:
М -> /V -> Л/' либо
N -> М -> М'. Для наблю-
дателя, расположенного в
соответствии с направлени-
ем проецирования перед
тройкой точек, в первом
случае будет «открытой», то
есть видимой, ближе распо-
ложенная к нему точка М.
Очевидно, что в этом случае
Рис. 4.2. Определение видимости прямой
при ее пересечении с плоскостью
90
|MMJ>j/VAf|, то есть видимой является более удаленная от плоскости
U точкам е с. Во втором случае имеет место ]/УМ
1
|>|ММ'], то есть
видимой является более удаленная от плоскости П точка N е Ф.
Следовательно, при ортогональном проецировании на плоскость П в
первом случае получаем на П изображение [&Т'М') видимого луча
[КМ) прямой с, а во втором - изображение [ЛГ'М') ее невидимого
луча, расположенное справа от точки К'. Очевидно, что произволь-
ное и единственное назначение точки М Ф К на прямой с не влияет
на результат анализа рассматриваемой видимости.
На рисунке 4.1, в соответствии с изложенным, дважды определе-
на видимость.
1. Видимость относительно плоскости проекций П
2
при помощи
фронтально-конкурирующих точек 2 € Ф и 3 е с; 2
2
= 3
2
, 2, Ф 3j. По-
скольку у
3
> у
2
, то есть точка 3 е с более удалена от плоскости П
2
чем точка 2 е Ф, то точка 3 видима при проецировании на П
2
и луч
[КЗ) прямой с является видимым при этом проецировании.
2. Видимость относительно плоскости проекций П
л
при помощи
горизонтально-конкурирующих точек 4 е с и 5 е Ф : Л
х
= 5
Ь
4
2
Ф 5
2
.
Гак как z
5
> z
4
, то есть точка 5 € Ф более удалена от плоскости Я,
чем точка 4 е с, то точка 5 видима при проецировании на П
х
и луч
[КЛ) прямой с является невидимым при этом проецировании.
Очевидно, определение видимости прямой имеет смысл при до-
пущении, что плоскость Ф представляет собой непрозрачную неогра-
ниченную либо ограниченную пластину бесконечно малой толщины.
На рисунке 4.3 на ос-
новании вышеуказанного
определена видимость пря-
мой с общего положения,
пересекающей проецирую-
щую плоскость Ъ LII
2
в
точке К при проецирова-
нии на П
у
, поскольку с
учетом указанного допуще-
Рис. 4.3. Модель построения ния, на плоскость П
2
пря-
пересечения прямой общего положения мая с проецируется как ви-
с проецирующей плоскостью димая.
91
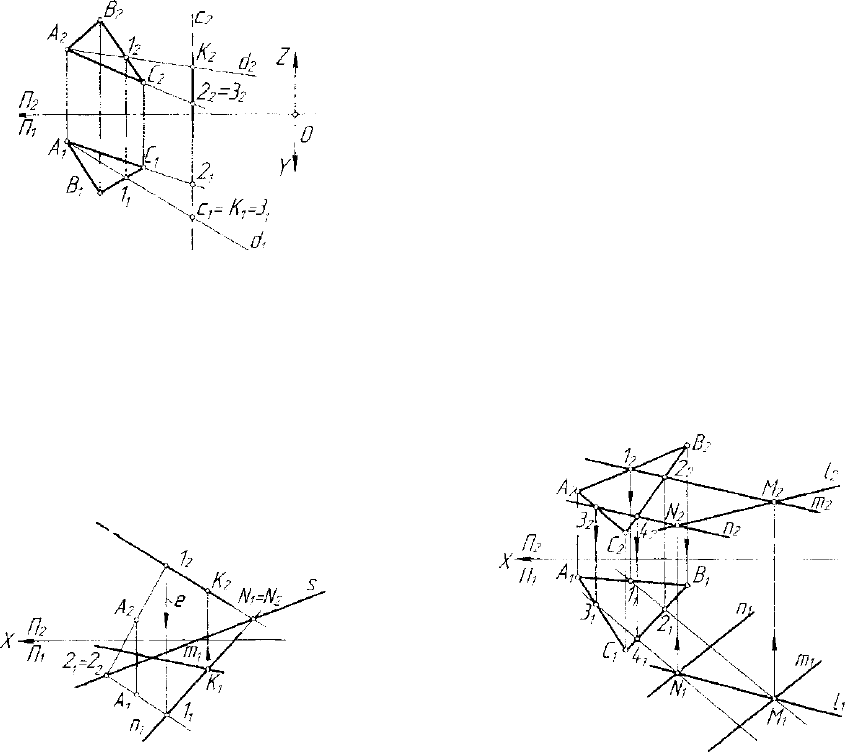
6. К, —> /С
7
e c
7
х-
Рис. 4.4. Модель построения
пересечения проецирующей прямой с
плоскостью общего положения
На рисунке 4.4 определе-
на видимость проецирующей
прямой сА-П
х
, пересекающей
плоскость Ф(ААВС) общего
положения в точке К. Для
анализа видимости прямой с
относительно плоскости Ф
при проецировании на П
2
ис-
пользуется пара фронтально-
конкурирующих точек 2 е Ф и
Зес, при этом у
3
>у
2
-
Рассмотрим определение
точки пересечения прямой и
плоскости, заданной на графи-
ческой модели родством. Пусть заданы: прямая т(т
1
,т
2
) и плос-
кость Ф(я,Д,Л
2
), где s - ось родства; А
Х
,А
2
- пара соответственных в
родстве точек, при этом /и<гФ (рис. 4.5). Требуется определить точ-
ку пересечения тоФ. Последовательность графического решения
рассматриваемой задачи имеет нижеследующий вид.
1. Строим прямую я,, соответственную прямой п
2
- т
2
в родст-
ве (s,A
u
A
2
). Для этого вначале
назначим точку 1
2
ея
2
. Затем
построим прямую 1
2
Л
2
и опре-
делим точку пересечения
1
2
~\
2
A
2
C\s. В пересечении
прямой 2, Л, и прямой е на-
правления родства определим
точку 1], соответственную точ-
ке 1
2
в родстве. Прямая
я, = (l
l
,N
l
) является искомой.
2. Определим проекции
искомой точки пересечения К:
ЛГ, = т
1
пп
и
К, -> К
2
ет
2
.
Рис. 4.5. Модель построения
пересечения прямой и плоскости,
заданной родством
92
4.2. Пересечение двух плоскостей
Исходя из формулы размерности пространства пересечения
(п. 1.7.2) две плоскости в пространстве Е
ъ
пересекаются по прямой
линии, поскольку $ = 2 + 2- 3 = 1. Эта линия может быть собственной,
либо несобственной. В последнем случае плоскости являются парал-
лельными. Рассмотрим решение задачи определения линии пересече-
ния двух плоскостей. Пусть на графической модели пространства за-
даны две плоскости общего положения ЩААВС) и А(т//п)
(рис. 4.6). Требуется построить их линию пересечения ZnA. Алго-
ритм решения данной задачи основал на алгоритме решения преды-
дущей задачи (п. 4.1) и включает по существу дважды повторенное
решение рассмотренной задачи. Действительно, для определения
прямой линии пересечения In Д необходимы, как и для всякой пря-
мой, две ее точки. Каждая из них определяется как точка пересечения
произвольной прямой, взятой в одной плоскости, с другой плоско-
стью. На основании сказанного последовательность конструктивного
решения поставленной задачи может быть нижеследующей.
1. В качестве одной из
двух прямых, необходимой
для определения одной из
двух точек искомой линии
пересечения, выберем пря-
мую т с Д. На основании
алгоритма определения точ-
ки пересечения прямой и
плоскости (п. 4.1) выполним
соответствующие построе-
ния и определим точку перс-
сечения тглЪ = М(М
1
,М
1
).
2. Выберем в плоскости
Д другую прямую, напри-
мер, п и определим точку пе-
ресечения ип1 = 7V(7V, ,N
2
).
3. Проведем линию
l=(M,N), которая и будет искомой линией пересечения /=Е гл Л .
Рис. 4.6. Модель построения пересечения
двух плоскостей общего положения
93
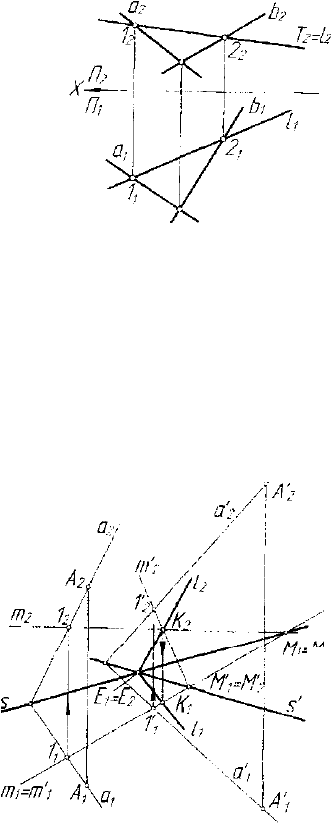
Если одна из двух пересекаю-
щихся плоскостей занимает относи-
тельно плоскостей проекций частное
положение, решение рассматриваемой
задачи значительно упрощается. Рас-
смотрим этот случай. Пусть на графи-
ческой модели заданы две плоскости
Pfanb) и Т 1 П
2
(рис. 4.7). Постро-
им их линию пересечения. Поскольку
одна из плоскостей, а именно, плос-
кость Г
?
является проецирующей, то
Т
2
= /
2
, то есть фронтальный след Т
2
плоскости Т есть одновременно и
фронтальная проекция искомой линии
пересечения /.
Рис. 4.7. Модель построения
пересечения плоскости общего
положения и проецирующей
плоскости
Поэтому ее недостающая проекция /, строится по принадлежно-
сти: /, пдг, = 1,; /, пй,
2
2
;1
2
•1, ей,; 2
2
-»2, е*,; (1„2,) = /,
Решение предыдущей задачи (рис. 4.6) может быть сведено к ре-
шению рассмотренной задачи, если одну из двух пересекающихся
плоское 1 ей преобразовать в
положение проецирующей
плоскости (рис. 3.27). Для это-
го потребуется всего одно
преобразование системы ос-
новных плоскостей проекций,
например: X—-—»Х--
1
.
Если на графической мо-
дели обе пересекающиеся
плоскости заданы родством,
например, Ф(л, А,,А
2
) и
Ф\^,А\,А'
2
), то последова-
тельность конструктивного
определения их линии пересе-
чения может быть нижесле- Рис. 4.8. Модель построения
дующей (рис. 4.8). пересечения двух плоскостей,
заданных родством
Г12
94
1. Проведем в поле "первых" проекций родственных соответст-
вий (s,A\,A
2
) и (s',A\,A'
2
) произвольную прямую m, =т\. Исполь-
зуя алгоритм построения проекций точки, принадлежащей плоскости,
заданной родством (рис. 3.16), построим "вторые" проекции т
2
и т'
2
прямых т и от', принадлежащих соответственно плоскостям: тсФ,
/и'с Ф'. Для построения этих проекций используются вспомогатель-
ные прямые асФ и а'сФ', проекции которых соответственны в
родстве: а,, а
2
-вродстве (s,A
{
,A
2
); а\, а\ -вродстве (s',A\,A'
2
).
2. Определим точку К по ее проекциям К
2
= т
2
Г\т'
2
,
К
2
—> К
х
е /71,, которые являются соответственными в обоих родствах
(s,A
x
,A
2
) и (s',A\,A'
2
).
3. Определим искомую линию / пересечения плоскостей по ее
проекциям, соответственным в обоих родствах: 1
2
-(К
2
,Е
2
);
/, = (К,, £,), где Е
]
=Е
2
= sf]s'.
4.3. Параллельность прямой линии и плоскости
В соответствии с формулой (1.5) определения степени парал-
лельности, прямая и плоскость в пространстве Е
ъ
вполне параллель-
ны, поскольку рц
=
~Л
=
^' ^
к
УР
се
стереометрии [7] известен при-
знак параллельности прямой и плоскости, формулированный в виде
следующей теоремы: если прямая, не лежащая в данной плоско-
сти, параллельна какой-нибудь прямой, лежащей в этой плоско-
сти, то она параллельна данной плоскости. Из признака параллель-
ности следует практическое указание для ее реализации на графиче-
ской модели пространства: построение прямой, параллельной данной
плоскости, требует предварительного проведения какой-нибудь пря-
мой в этой плоскости. Логическая неопределенность "какая-нибудь" в
признаке параллельности позволяет заданием дополнительных усло-
вий выделить однопараметрическое множество (пучок) прямых или
единственную прямую из двухпараметрического множества прямых в
плоскости, удовлетворяющих условию параллельности. В подтвер-
ждение сказанного рассмотрим пример. Пусть на графической модели
(рис. 4.9) заданы: плоскость общего положения Ъ(а//Ь), точка
C(C,,C
2
)£l и проекция т
2
прямой т. Требуется построить полную
модель прямой mim^nh) по условиям: Сет, т II2 . Очевидно, этими
95
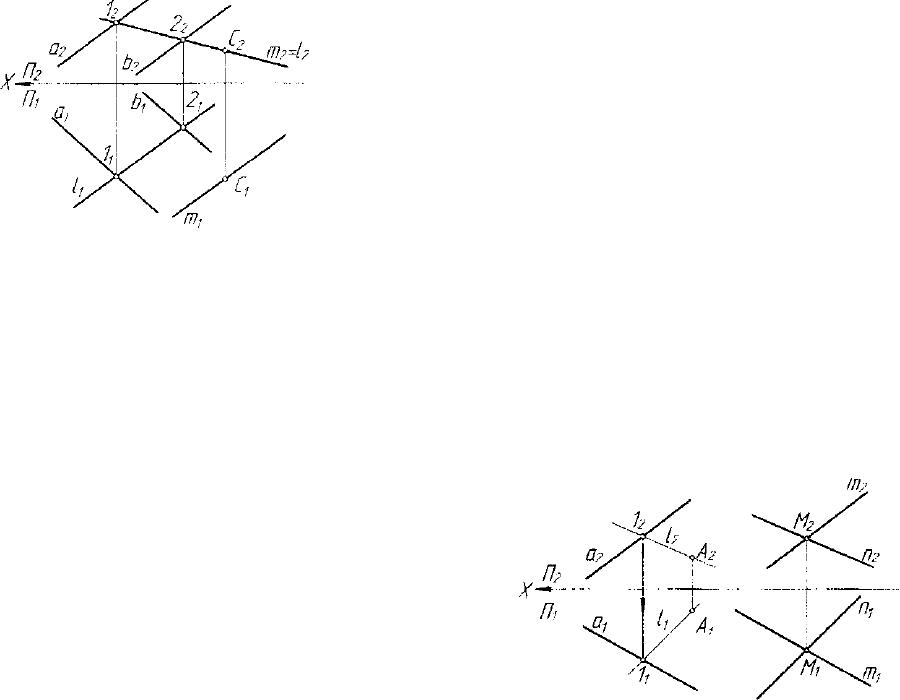
условиями определена един-
ственная прямая т простран-
ства. Действительно, парамет-
рическое число прямой про-
странства Е
3
, на основании
формулы (1.1), равно D™=4.
Определим размерность усло-
вия прохождения прямой про-
странства через точку. По
формуле (1.4) размерность
этого условия <4л) вычисляет-
ся следующим образом:
Рис. 4.9. Модель построения прямой
линии, параллельной плоскости
(2-3-1И1 + 1)
•(3
+
0)
=
2.
Признак (условие) параллельности прямой и плоскости про-
странства Е
3
имеет размерность, вычисляемую по формуле (1.6):
Q,, = 1 • 1 -(3-1 -2 + 1 • I)- 1. Условие задания одной проекции т
2
ис-
„ 1,0
комой прямой
т
имеет символическое представление:
е
2
>0
,
и его
раз-
мерность может быть вычислена по формуле (1.4) следующим обра-
зом:
Таким образом, сумма размерностей указанных условий задачи
равна Q
o6
{^) + Qii+Q
o6
{exo) =
D
n = 4,
что
говорит о корректности
поставленной задачи и единственности ее решения. На основании
признака рассматриваемой параллельности и проведенного анализа
условия задачи выполним ее конструктивное решение в следующей
последовательности:
1. т
2
п а
2
= 1
2
, nb
2
=2
2
;
2. 1
2
->1,
еа,, 2
2
->2, е/>,;
3.
0„2
|
) = /
1
;
4. щП\
х
, С, еот,.
Построенная прямая т^пц,)?^) является искомой. Вспомогатель-
ная прямая Щ
х
,1
2
-щ) является, в соответствии с отмеченной выше
логической неопределенностью "какая-нибудь", прямой пучка парал-
96
лельных прямых в плоскости X, выделенного из двухпараметрическо-
го множества прямых этой плоскости условием задания проекции
/
2
= т
2
прямой /. Это условие, как было показано выше, имеет раз-
мерность Q
o6
(e
2
^
0
) = }.
4.4. Параллельность двух плоскостей
В соответствии с формулой (1.5) степени параллельности две
плоскости
1
+
1
в пространстве Е
3
вполне параллельны, поскольку
Р/1
= 1. В стереометрии [7] известен признак параллельности
двух плоскостей, выраженный следующей теоремой: если две пере-
секающиеся прямые одной плоскости соответственно параллель-
ны двум прямым другой плоскости, то эти плоскости параллель-
ны. Из признака параллельности следует практическая рекомендация
по определению плоскости, параллельной данной: необходимо про-
вести две пересекающиеся прямые в данной плоскости, а искомая
плоскость определится парой пересекающихся прямых, соответствен-
но параллельных проведенным пересекающимся прямым. Рассмотрим
решение задачи. Пусть
на графической моде-
ли заданы плоскость
Ъ(А, а) и точка М <£ £
(рис. 4.10). Требуется
построить плоскость Л
по следующим усло-
виям: Me А, А//Е.
Этими условиями оп-
ределяется единствен-
Рис. 4.10. Модель построения параллельных
ная
плоскость. Дейст-
плоскостей вительно. Параметри-
ческое число плоскости пространства Е
3
, согласно формуле (1.1),
равно D™ - (3 - 2) • (2 +1) = 3. Условие прохождения плоскости через
точку имеет символическое представление е^о»
и его
размерность
определяется в соответствии с формулой (1.4) следующим образом:
/\ , 2.1ЛК
(2-3-2)-(2 + 1)
(3 +
2
+
0)
=
1.
97
Учитывая, что две плоскости в пространстве Е
3
вполне парал-
лельны, поскольку их степень параллельности по формуле (1.5) равна
Pn
=
^Г~
=
^'
0П
Р
е
Д
елим по
формуле (1.6) размерность этой парал-
лельности: Q
lt
=1-2 -(3-2-2 + 1-2) = 2. Таким образом, получаем
равенство параметрического числа плоскости пространства и суммы
размерностей условий задачи:
Следовательно, условия рассматриваемой задачи корректны и
она имеет единственное решение.
Алгоритм решения задачи в соответствии с признаком парал-
лельности может быть нижеследующим
1. В плоскости проекций 77
2
проведем линию А
2
е /
2
;
2. /
7
ел а
2
= 1
2
'•>
3. 1
2
—» 1, ЁЙ,;
4. (1„4) = V.
5. т
2
II а
2
, М
2
е от
7
. т
х
II а
х
, М
х
е гп
х
;
6. п
2
II /
2
, М
2
е и
2
, л, /7 /[, Л/, е /г,.
Искомая плоскость А определена двумя пересекающимися пря-
мыми т(т
х
,т
2
) и «(«,, л
2
), при этом mil и, п/11.
Решение данной задачи можно представить как дважды повто-
ренное решение предыдущей задачи (п. 4.3). Действительно, из при-
знака параллельности двух плоскостей следует, что если каждая из
двух пересекающихся прямых параллельна плоскости, то плоскость
этих прямых параллельна этой плоскости. Поэтому вышеприведен-
ный алгоритм можно представить в следующем кратком виде:
1. тИИ, М ет;
2. nllzZ, М е п.
4.5. Перпендикулярность прямой и плоскости
Прямая и плоскость в пространстве £
3
вполне перпендикулярны,
так как согласно формуле (1.8) степень их перпендикулярности равна
0 + 1
1 г,
р
х
= —— = 1. В стереометрии известен признак перпендикулярности
прямой и плоскости [7], выраженный следующей теоремой: если
прямая перпендикулярна двум пересекающимся прямым, лежа-
98
1цим в плоскости, то она перпендикулярна этой плоскости. В со-
ответствии с признаком, для построения прямой, перпендикулярной
данной плоскости, необходимо в этой плоскости предварительно про-
вести две пересекающиеся прямые, а затем добиваться перпендику-
лярности искомой прямой каждой из проведенных пересекающихся
прямых. Таким образом, решение задачи о перпендикулярности пря-
мой и плоскости основано на решении задачи о перпендикулярности
двух прямых (пересекающихся или скрещивающихся). Рассмотрение
перпендикулярности двух прямых на графической модели основыва-
ется на теореме о проекции прямого утла: если одна сторона прямо-
го угла параллельна плоскости проекций, а другая ей не перпен-
дикулярна, то на эту плоскость проекций прямой угол проециру-
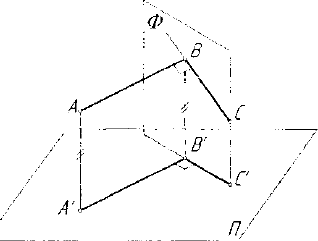
ется без искажения. Рассмотрим доказательство этой теоремы. 11усть
ZABC = 90°, стороны прямого угла удовлетворяют условиям: сторо-
на А В параллельна плоскости проекций П; сторона ВС не перпен-
дикулярна и не параллельна плоскости проекций П (рис. 4.11). До-
кажем, что /.А' В' С=90°. По-
скольку АВ I! П и А' В' есть ор-
тогональная проекция стороны
АВ, то АВИ А'В'. Прямая А В
перпендикулярна плоскости
Ф(ВСГ\ВВ'), где В В' - проеци-
рующая прямая (ВВ'1 Л). Дей-
ствительно. АВ ± ВС но усло-
вию теоремы и ABLBB', так
как ВВЧП и АВ//П. На осно-
вании признака перпендикуляр-
ности прямой и плоскости сле-
дует, что АВ ± Ф. Из известно-
го в стереометрии определения прямой, перпендикулярной плоскости
[7]: прямая называется перпендикулярной плоскости, если она
перпендикулярна любой прямой, лежащей в этой плоскости - из
этого определения следует, что перпендикулярная прямая перпенди-
кулярна любой прямой в этой плоскости. Поэтому из перпендикуляр-
ности АВ _1_ Ф следует А В X В'С, поскольку Д'С'сФ как линия пе-
ресечения ФпП = В'С. А поскольку АВИА'В', то А'В'1В'С, то
есть Z.A' В'С— 90°. Если ВС//Л, то утверждение теоремы очевидно.
Рис. 4.11. Интерпретация теоремы о
проекции прямого угла
99
