Волков В.Я. и др. Курс начертательной геометрии на основе геометрического моделирования
Подождите немного. Документ загружается.

ГЛАВА 2. ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ЕВКЛИДОВА ПРОСТРАНСТВА
В геометрии известны следующие методы моделирования абст-
рактных пространств: аналитический, конструктивный и аксиомати-
ческий [16, 24]. При аналитическом моделировании в зависимости от
структуры исходного пространства применяют различные системы
координат. В случае евклидова пространства, характеризующегося
линейной структурой, применяются: декартова, сферическая, цилинд-
рическая системы координат. Для аффинного и проективного про-
странств применяются соответственно косоугольная и проективная
системы координат. Для моделирования линейчатого пространства с
основным объектом - прямой линией, характеризующеюся квадра-
тичной структурой, применяют плкжкеровы координаты, удовлетво-
ряющие однородному квадратному уравнению [17, 28].
В случае конструктивного моделирования исходное пространство
и его модель связаны некоторой проекционной системой, включаю-
щей проецирующие линии и поверхности. Такое моделирования дос-
таточно очевидно и наглядно. Оно является основным методом ис-
следования в классической начертательной геометрии.
При аксиоматическом моделировании отсутствует конструктив-
ная проекционная связь между исходным пространством и его моде-
лью - пространством образов. Важным критерием существования ак-
сиоматической модели исходного пространства является равенство
размерностей основного объекта пространства и его образа на модели
и сохранение структуры пространства на его модели.
2.1. Конструктивные модели пространства Е
п
В главе 1 было показано, что операция проецирования устанав-
ливает однозначное отображение точек {А е £„)-» (Л'е П
2
), однако
она не позволяет установить обратное отображение А'-+ А. Поэтому
утверждается, что поле точек 11
2
не является моделью пространства
Е
п
. С практической точки зрения чрезвычайно важно, чтобы отобра-
жение Е„ —> П
2
было взаимно однозначным почти для всего про-
странства Е
п
. Термин "почти" означает, что отображение Е
п
<-> П
2
будет взаимно однозначным кроме конечного числа подпространств
Е„ и конечного числа точек и прямых плоскости П
2
. Если такое ото-
бражение получено, то говорят, что построена обратимая модель про-
странства £„ на плоскости П
2
. Смысл обратимости состоит в том,
что по заданному образу точки на П
2
можно восстановить прообраз
этой точки в Е„. Однако образом не может быть точка, так как двух-
параметрическое множество точек П
2
не эквивалентно п парамет-
рическому множеству точек Е
п
: оо
2
Ф СО". Следовательно, образом
должна быть некая фигура Ф е П
2
, состоящая из конечного числа то-
чек и прямых, связанных условиями инцидентности в определенном
порядке. Например, это может быть к точек (А:-вершинник, полный
к -угольник) или к прямых (А-сторонник), пригодные для модели-
рования четномсрных пространств Е
2к
, это могут быть кривые (ок-
ружности, параболы, эллипсы и гиперболы для моделирования £
3
,
Е
4
, Е
5
соответственно), множества кривых и др.
Поскольку в данной главе мы имеем дело с линейным простран-
ством, то использовать в качестве образов кривые линии нет необхо-
димости. Ограничимся только фигурами, состоящими из точек и пря-
мых. Пусть пространство Е
п
четномерно: п = 2к. Тогда, используя к
операций проецирования из (я-З)-мерных центров 5,',_
3
, i-\,...,k
на плоскость П
2
, получим к точек А' е П
2
в качестве образа точки
А € 5„. Возникает вопрос, как должны быть выбраны центры
{Sl,_
3
}<zE„, чтобы отображение (А е Е„) О ({А
1
} с П
г
) было обра-
тимым? Для ответа на него будем рассуждать следующим образом.
Пусть 5^_
3
выбраны в Е„ совершенно независимо друг от друга. То-
,i к . Yi
гда /А[ ,S'
N
_
3
) = P
L
N
_
2
. Можно заметить, что Г\К-2 = Л, где к = . Дей-
СТВИТеЛЬНО, Р^
2
Г\Рп-2 -
E
n-4 '
E
n~S\
P
n-2
=
Е
п-Ь
>
Е
п-бС\Р*-2 =
Е
п-К>
E
n 2kl2
f)P*-2
=
Е
п-2к
=
Е
о =
А
- Таким образом, условие обрати-
мости модели пространства Е
п
для точки удовлетворяется. По удов-
летворяется ли условие обратимости для прямой? Прямая задается
двумя точками А е Е
л
и В е £„, А Ф В. Те же к операций проециро-
вания породят на П
2
к образов прямых /т"В', для которых будет со-
блюдаться проективное соответствие точечных рядов:
(А,В,С,...)л(А',В',С,...), i = l, к. Следовательно, на П
2
будут
41
40
порождаться проективные соответствия рядов (А ,В ,С ,...)л
л(А
2
,В
2
,С
2
,...)л... л(А
к
,В
к
,С
к
,...). Но эти проективные соответст-
вия будут служить моделью прямой АВ в том случае, если будут из-
вестны по три точки из каждого точечного ряда. А наша конструкция
позволяет иметь на П
2
только по две точки А' и В', так как
S'„_
3
f]n
2
=0- Таким образом, условие обратимости модели для пря-
мой не удовлетворяется. Следовательно, центры проецирования S'
n
_
3
не могут выбираться в Е
п
произвольно, независимо друг от друга.
Рассмотрим другой случай. Пусть {^.,}сР„_
2
с£
й
. Тогда
Р„_
2
Г)П
2
=0. Пусть выбрана точка ЛеЕ„, А^Р
П
_^. Тогда
(А, Р
п
_
2
\ - Р
п
_
:
и Р
П
_
Х
Г\П
2
=Ь
Х
, ОеЦ. Имеем следующее:
(A, S'„.3) = PJ,
2
с Р„ .,, Р1_
2
П Ц = А
1
. Следовательно, А
1
е L,,
/ = 1,...,и-1. Моделью точки АеЕ
п
на 11
2
будет множество точек
А' б L,. Проверим обратимость модели. Пусть произвольно заданы
точки А' €£,; / = -1. Имеем [A\S'^
3
) = />
п
'_
2
с Р„ ,,
^20^2=^.3^^-1, ^-зП^-2 = ^-4с:Р
п
.... Я,ПС"2 =
= £<, = /1 е . Таким образом, модель точки АеЕ„, представляю-
щая собой множество A' ei,, L, э0. i = l,,..,n-\, является обратимой
для точки.
Проверим обратимость модели для прямой АВсЕ
п
,
ABf}P„ : -0- Будем иметь: (А, В, С,...) л (А
1
, В',С',...), / = 1, ...,«-1,
(A,B,C,-)A(Lf,Lf,!!{,...).
Поскольку Ц*эО, ifaO, эО, то (Л
1
,5
!
,С',...)л
л(А~,В ,С
2
,...)л...л(А"~
}
,В"~
1
,С"~
Л
,...). Перспективное соответст-
вие точечных рядов задается двумя парами соответственных точек,
поэтому получаемая модель обратима для прямой АВ. Из этого непо-
средственно следует, что модель обратима для двух пересекающихся
прямых, т.е. - для плоскости, для трех пересекающихся в одной точке
прямых, т.е. - для 3-плоскости и т.д.
Изменим рассмотренную конструкцию таким образом, чтобы мо-
дель точки А представляла собой множество точек
[U'jc/^aOlU \А"-
2
&И
2
\, А"-
2
е1
л
, i = l, ...,«-3. Это означа-
42
ет, что центры проецирования S'
n
_
2
cz Р„^
2
, но S^_
2
cztP„,
2
. Тогда для
любой точки А е Е
п
, А& Р
п
_
2
получим выбранную модель, которую
проверим на обратимость. Для множества точек j^'jczL,, Lj э 0 по-
лучим i подпространств Р„'_
2
сР
и
_,, пересечением которых будет
единственное подпространство Е
2
аР
пА
. Тогда E
2
f](^A
n
'
2
,S",Z
2
) =
= Е
0
= А, Л е Р
п л
. Следовательно, модель обратима для точки.
Чтобы получить обратимость модели для прямой АВ, на
плоскости П
2
необходимо получить исключенную точку
О = Р„-
2
Г\П
2
, которая будет центром пучка прямых (Ц, Lf, L\ , ...) л
л (А, В, С, ...), и исключенную прямую т = P„_.
x
f\ll
2
, которая будет
носителем третьих точек проективных рядов {А"'
2
, В"~
2
, М"
2
, ...) л
(А, В, М, ...), где М = АВ f]P„_
x
. При этом Оет. Прямая АВ с Е„,
AB(Z.P
n2
, будет иметь моделью соответственные точечные ряды
(А, В, С,
..АлЩ',
I», 4',
...),
(А\ В\С
Х
, ...) л
(А
2
,В
2
,С\
•••)
л
X ...л (А"'
3
, В"~\ С"-
3
, ...), (А, В, М, ...)л (Л
и_2
, В"'
2
, М"
2
, ..,),
(А"~
2
,В"~
2
,М
П
-
2
, ...)л {AZ,B\M\ ...), где М' = Л*В'Г\т, i = 1,
п - 3. Это возможно в том случае, если центр S"Zl будет относитель-
но Р„_
2
не в общем положении, а в частном. Именно,
S
n
J\\P„.
2
=
S"„-J.
Тогда
(s"
n
:lP
n
_
2
)
= P
n
_
x
.
Пусть модель точки А представляет собой множество
[A
1
cL
x
эО] IJ К'
-4
еЛ
2
,/
3
еЯ
2
], А"~
4
eL
x
, А
П
ЫЦ, / = 1,
n - 5. Рассуждая аналогично, можно доказать ее обратимость.
Моделью прямой АВ с Е
л
, АВ <Х Р
п2
будут па П
2
соответст-
венные точечные ряды, аналогичные приведенным выше. Однако
центры 5^Г
3
и 5*^ J должны быть не в общем положении относитель-
но и
относительно друг друга, а - в частном. А именно,
необходимо, чтобы S"Z$ П Р„ г - >
s
"-l\\
P
n-2 ~
[S"Z*,Р„-
2
)
=
(Зп-1>
р
п
-г)
=
Р
п-\
-
в этом
сл
У
чае
модель
будет
обрати-
ма для прямой.
43
Продолжая этот процесс, мы придем к выводу, что вес центры
проецирования о„_
3
, i = l, должны принадлежать гиперплоско-
сти Р
п
_
{
пространства #
я
.
Пусть пространство Е
п
нечетномерно: « = 3,5,7,.... Тогда усло-
вие расположения центров проецирования {S'
n
3
} с Р
п
_
2
с Е
п
, i = 1,...,
п-1, порождает обратимую модель на плоскости П
2
• Доказательство
этому будет аналогично доказательству в случае четномерного про-
странства.
Выводя из подпространства Р
п
_
2
центры S'
n
_
3
один за другим,
получим модель, состоящую из точек [{А'\ с L
l
,L
l
э 0] (J [А' е //,],
А> г А,, 0=Р
я
_
2
ПЯ
2
,£, =Р
И
.,П^2-
Существование гиперплоскости необходимо для выполне-
ния условия проективности точечных рядов при получении модели
прямой пространства Е„. В конечном итоге будут получены точки
п-1
А' еЯ
:
, j = 1, и прямая сЯ
;
, L, эО. Центры проекций
5,',..
3
и Р
п
2
должны располагаться в одной гиперплоскости Р„_,.
Подробное исследование таких конструкций выходит за рамки
настоящей книги. Поэтому рассмотрим более подробно только одну
из них, а именно ту, у которой [S'
n
_~} с: Р
п
_
2
с Е
п
, и независимо от
размерности пространства.
Пусть в пространстве Е
п
задана декартова система координат
Ох
х
х
2
...х
п
. Пусть плоскость проекций Я, совпадает с плоскостью
Ох
х
х
2
. Тогда оси 0х
(
, / = 3,...,«, будут перпендикулярны плоскости
Я
2
= Ох
х
х
2
. Пусть проецирование на Я
2
будет ортогональным. Тогда
центры проецирований S'
n
_
2
должны быть бесконечно удаленными и
должны принадлежать (я - 2)-плоскостям в следующем порядке:
S^
3
с:<9л
3
...х„,
5„'_з с Ох
2
х
4 '
б
1
^'^ сОь^Х/...!..
Эти центры порождают следующие проекции:
Лр
5
1,«
(
А
)
= Л
е
0x
i
x
2
=
п
\,
п-Ъ
Пр
2
^А) = А
2
еОх
1
х
3
=П
2
,
Up
3/а
(А) = А
3
е Ох
х
х
А
= II
3
,
'V-3
Л/Vi,» (4) = Л-1
е
<?*л = •
«-3
Поскольку все эти проекции двумерны, то обозначать размер-
ность нижним индексом нет смысла. Поэтому, следуя традиции, ниж-
ний индекс будет обозначать порядковый номер проекций.
Так как у всех проекций есть общая ось Ох,, то плоскости
П
2
,....,П„-\ можно развернуть вокруг оси Ох
{
на 90° до совпадения с
плоскостью проекций /У,. Тогда оси Ох
2
,Ох
3
,...,Ох„_
1
совпадут. Та-
ким образом, модель пространства будет иметь две оси: ось Ох, и
перпендикулярную ей ось Ох
2
= Ох
3
= ... = Ох„.
л
.
2.2. Аксиоматические модели пространства Е
н
Из того, что было изложено в п.п. 2.1, следует, что в пространст-
ве Е„ должны быть выделены два исключенных подпространства
Р„_
2
и
Р
п
-\ > Л>-2 сР„ ,. Построенные конструкции позволяют моде-
лировать все пространство Е
п
, кроме этих двух подпространств. Это
пе означает, что на плоскости проекций нет образов, моделирующих
P
n
_i и Р„_
х
. Просто изучение этих образов есть предмет серьезного
научного исследования и не является нашей задачей. Поэтому, в дан-
ном случае, будем считать, что все точки подпространств P
n 2
и Р„_,
являются исключенными.
На плоскости проекций П
2
будут существовать два исключен-
ных элемента: точка Р = P
n
..
2
С\П
2
и прямая I = Р
П
_
Х
Г)П
2
, Pel. В
силу приведенных в п.п. 2.1 условий подпространства Р
п
^
2
и Р
п
_
{
могут быть выбраны произвольно. Это означает, что исключенные
точка Р е П
2
и прямая / е II
2
тоже могут быть выбраны произволь-
ны. Таким образом, модель пространства Е„, построенная без конст- ,
v
руктивной связи с Е
п
, будет называться аксиоматической моделью.
45
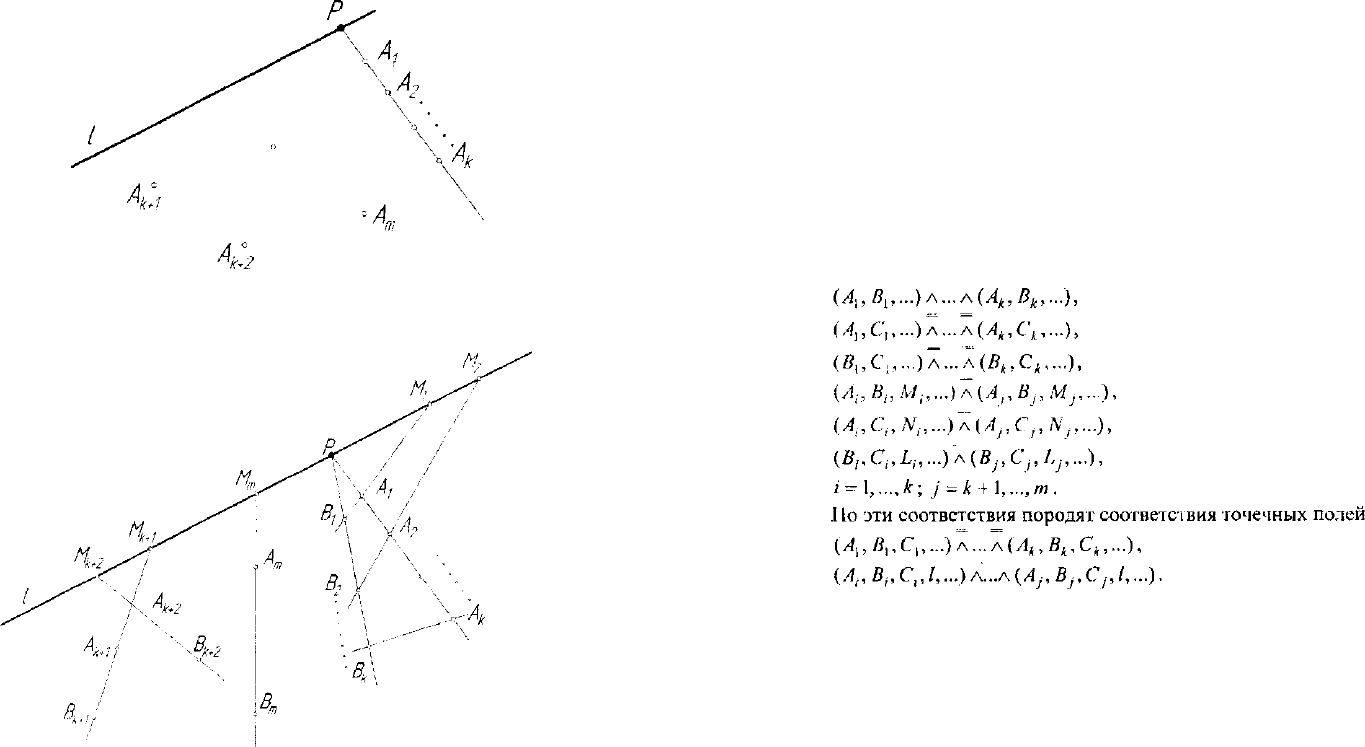
Ее общий вид для точки А е Е„, А <£ Р
пЛ
представлен на рисунке 2.1,
где к + 1 + 2т = п. На рисунке 2.2 приведена модель прямой АВ е Е„,
АВаР„
л
.
Рис. 2.1. Аксиоматическая модель пространства Е
п
Рис. 2.2. Модель прямой АВ пространства Е
п
Модель прямой АВ включает в себя условия перспективного и
проективного соответствия точечных рядов:
46
(А
1
,В
и
...)л(А
1
,В
2
,...)л...л(А
К
,В
К
,...)
>
(A
i
,B
i
,M
I
,...)A(A
J
,B
j
,M
j
,...),
(2.1)
i = l,...,k; j = k + \,...,m.
Исходя из этого, можно доказать существование модели плоско-
сти ABC с: Е„, АВС&Р
п
_
л
, модели 3-плоскости ABCD а Е
п
,
ABCD от Р
п
_
1
и так далее, вплоть до гиперплоскости пространства Е„.
Все 2-плоскости, 3-плоскости, гиперплоскости будем считать на-
ходящимися в общем положении относительно проекционной систе-
мы, отображающей пространство Е
п
на плоскость.
Сначала покажем, что представляют собой модели перечислен-
ных подпространств, а потом подтвердим эти модели расчетом пара-
метров.
Пусть требуется построить модель 2-плоскости ABC. Будем
иметь:
В последнем соответствии прямая / соответствует сама себе.
3—плоскость задается четверкой независимых точек
(A, B,C,D,...), моделями которых являются (А
}
, А
2
,А
т
),
(B
v
B
2
,...,B
m
), (C
u
C
2
,...,C
m
),(D
l
,D
2
,...,D,„). На плоскости модели
существуют
особые точки О
х
=0
2
=...-О
к
- Р, О
к+]
el,
О
к+2
el,
О
т
el, по отношению к которым четверки точек A
i
,B
j
,C
i
,D
i
лежат
на соответственных лучах.
Если 3-плоскость рассматривать как однопараметрическое мно- »
жество (пучок) 2-плоскостей, то на плоскости модели будут сущест-
вовать однопараметрические множества проективных соответствий
(2.2)
47
точечных полей. Тогда произвольное множество точек (Е,,...,Е
т
) бу-
дет моделировать точку Ее Р
п
, но не принадлежащую гиперплоско-
сти (ABCD). А множество точек (E
1
A
1
B
1
C
1
D
1
)A(E
2
A
2
B
2
C
2
D
2
)A...
л(E
m
A
m
B
m
C
m
D
m
) будет моделью точки Е, принадлежащей гиперп-
лоскости (ABCD).
И так далее.
Размерность множества прямых пространства Е
п
равна 2(п-\).
Задание элементов модели одной точки требует I + к + 2(т - к) пара-
метров, двух точек - соответственно 2[1 + к + 2(т - к)] параметров.
Следовательно, 2[1 + к + 2(т - к)] = 2и. Проективность прямолиней-
ных рядов задается двумя парами точек (третья лежит на исключен-
ной прямой /). Поэтому имеем 2п - 2 = 2(п -1).
Размерность множества плоскостей пространства Е
п
равна
3(я-2). Плоскость задается тремя точками, что на модели требует
задания 3[1 + к + 2(т - it)] параметров. Проективное соответствие за-
дается тремя нарами точек, что требует задания 6 параметров, кото-
рые необходимо вычесть из суммы параметров. Имеем
Зи-6 = 3(и-2).
Размерность множества 3—плоскости пространства Е„ равна
4(л-3). 3-плоскость задается четырьмя точками, что потребует
4[1 + к + 2{т - к)] параметров модели. Но модель 3-плоскости требует
задания любых двух проективных соответствий двух плоских полей,
т.е. получим 4[1 + к + 2(т - к)] -12 = 4и -12 = 4(л -3).
И так далее.
Рассмотрим построение точки, принадлежащей заданному под-
пространству, используя для этого только модель пространства.
Предварительно выясним, сколько параметров можно задать
произвольно. Прямая «-мерного пространства задается аналитически
системой линейных уравнений
f
1
(x
l
,x
2
) = О
J /
2
(*1
5
*з) = °
Очевидно, что задание одного любого параметра х,,...,х„ позво-
ляет построить точку данной прямой.
48
2—плоскость и-мерного пространства аналитически задается сис-
темой линейных уравнений
J](
x
l>
х
2>
х
з)
~
О
^fn(
x
]'
X
2'
X
n) ~®>
из которой видно, что произвольно можно задать любые два парамет-
ра.
Продолжая этот процесс, придем к выводу, что для задания точки
к -плоскости произвольно можно задать к любых параметров.
Построение модели точки С, принадлежащей прямой АВ, осу-
ществляется на основе проективных соответствий (2.1). Для построе-
ния необходимо задать произвольно только один параметр, например,
задать прямую пучка (Р). Тогда получим к точек С, ее, С
2
ее,
С
4
ее, а проективные соответствия позволят построить точки C
/t+]
,
С
т
на прямых А
к+1
В
к+и
А
т
В
т
.
Построение модели точки D, принадлежащей плоскости ЛВС,
осуществляется следующим образом. Для построения необходимо за-
дать произвольно два параметра, например, задать прямую d пучка
(Р) и одну точку на ней D
{
€c/. Тогда проективные соответствия
(2.2) позволят построить точки D
2
, D
3
, D
k+i
и все остальные точ-
ки D
k+2
, D
m
полей (A
k+2
,B
kl2
,C
k
,
3
,l),..., (А
т
,В„„С
т
,1).
Построение модели точки Е, принадлежащей 3-плоскостп
ABCD, можно выполнить по следующему алгоритму. Для построения
необходимо задать произвольно три параметра, например, задать
прямую е пучка (Р), две точки на ней £, ее, Е
2
ее
- Тогда проек-
тивные соответствия (с, d,е,/,...) л (C
k+l
, D
k+)
, Ек+i,М
кл
,,...) позво-
ляют выделить в иоле (A
kn
,B
ku
,C
k
^,D
k
^
u
l) подполе
(А
к+1
,В
к+1
, Ек+\,1)- После этого можно перейти к задаче построения
точки E
k+l
z(A
k+2
,B
k
^
2
,E
M
,l), E
m
e(A
m
,B
m
J:
m
,l), т.е. к задаче
на принадлежность точки плоскости.
И так далее.
В качестве примера рассмотрим модель 3-плоскости ABCD пя-
тимерного пространства и построение принадлежащей ей точки Е.
Пусть модель 3 -плоскости ABCD имеет вид (рис. 2.3):
0(а, Ь, с, d) - пучок прямых с центром О,
49
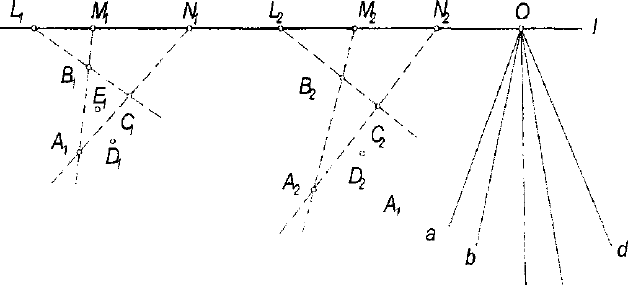
{A
X
,B
X
,C
X
,D
X
} - четыре точки 1-го поля,
{A
2
,B
2
,C
2
,D
2
} - четыре точки 2-го поля.
Проективные отношения между этими множествами следующие:
(1,А
Х
,В
Х
,С
Х
,..УМ1,А
2
,В
2
,С
2
,...),
(1,A
x
,B
x
,D
x
,^..)A(1,A
2
,B
2
,D
2
,...),
0(1, а,Ь,...)л (М
х
,А
Х
,В
Х
,...), М
х
=А
1
В
1
[)1,
0(1,а,с,...) л (N
x
, А
х
,С,,...), N
x
= А
х
С,Г]/,
0(1,Ь,
с,...)
A
(L
x
, В
х
, С,,...),
L
x
=В
Х
С,П/.
С \
е
Рис. 2.3. Модель 3-плоскости ABCD
Произвольно задаются: луч Ое и точка Е
х
. Па прямой / найдется
такая точка 0\, для которой четверка лучей О
х
А
х
, 0\В
Х
, 0\С
Х
, 0\Е
Х
и
четверка лучей Оа, Ob, Ос, Ое будут образовывать одно и то же
сложное отношение Я. На прямой / найдется и такая точка 0\, для
которой четверка лучей 0\А
Х
, 0\В
Х
, 0\D
X
, 0\Е
Х
и четверка лучей Оа,
Ob, Od, Ое будут образовывать одно и то же, но другое, сложное
отношение Я. По сложным отношениям Я и Л на прямой / находятся
точки Oi и Oi, и, соответственно, лучи ОгЕ
2
, ОгЕ
2
, пересечение ко-
торых есть точка Е
2
. Следует заметить, что этот общий алгоритм не
50
единственный. Могут быть и другие способы построения модели точ-
ки Е(е,Е
х
,Е
2
).
Из всего сказанного можно сделать важные выводы:
1) если моделируемое пространство обладает линейной структу-
рой (пересечение любых линейных подпространств есть линейное
подпространство, и линейное расширение любых линейных подпро-
странств есть линейное подпространство), то модель этого простран-
ства тоже обладает линейной структурой (все соотношения между
элементами модели перспективные и проективные, т.е. линейные);
2) если размерность моделируемого пространства больше раз-
мерности пространства модели, то в пространстве модели должны
существовать исключенные элементы (точки, прямые, плоскости, ...).
Дадим важные для дальнейшего изложения определения струк-
туры пространства и структуры модели.
1. Структурой /7-мерного пространства называется упорядо-
ченный набор (а
и
,а
1
,...,а
п Х
,В), где a
t
- множества, элементами ко-
торых являются /'-плоскости; В - множество бинарных отношений,
В £ ы,- ха
г
Если А е a
t
и а ея-, i< j, то бинарное отношение есть
отношение инцидентности: "А принадлежит а" или "с/ проходит че-
рез А ".
2. Если a
(
f|a- = a
k
, то структура пространства называется ли-
нейной. В противном случае структура пространства нелинейная.
Например, все точечные линейные пространства обладают ли-
нейной структурой. Любое подпространство таких пространств ана-
литически описывается системой линейных уравнений.
Если в качестве основного элемента пространства выбрана пря-
мая, то такое пространство будет обладать нелинейной структурой.
3. Структурой модели «-мерного пространства на плоскости
называется упорядоченный набор ({/„},\у
х
\,.-,{у„.
х
},8), где {/-} -
множества, элементами которых являются плоские фигуры у у, S -
множество бинарных отношений, ^с{/,}х {у.).
4.
Если
{ftHKi'-'fi,"}
и
если
Yij*Yi,k>
J*
k
'
то
структура
модели называется линейной.
Рассмотрим модель четырехмерного пространства, основным
элементом которого является точка. Пространство будет линейным,
что подтверждается системой аксиом принадлежности. Докажем, что
модель
51
A-+(A
U
A
2
);
АВ -> [(Л, Я,),(А
2
,В
2
)],(Д,В
{
, М,,...) л (А
2
,В
2
,М
2
,...);
ляс -> [(4 д,с,), (4, в
2
, с
2
)], (4, в,, с,, /,,...) л (А
2
, в
2
, с
2
, /
2
,...);
ABCD -> [(/1,В,С,Д \(A
2
,B
2
,С
2
,D
2
)},
(А, Д,,С,,/„...) л ,£
2
,С
2
,/
2
,...), (Л,,В,, Д,/,,...) А (Л
2
, Я
2
,D
2
,/
2
,...)
линейна и структура пространства изоморфна структуре модели. Дей-
ствительно. Выполняются следующие условия:
1. Две плоскости пересекаются в точке ABCC\DEF = G.
Тогда на модели получим
(А
1
,В
1
,С
]
,1
]
,...)л(А
2
,В
2
,С
2
,1
2
,...),
(D„ £
lf
F„/„...) л (D
2
,£
2
,F
2
,/
2
,...).
Если G e ABC и G e DEF, то (G,, G
2
) должна быть и нвариант-
ной парой в этих проективных соответствиях. Пусть /, = /
2
, по /, Ф1
2
.
Тогда /j = 1
2
есть инвариантная прямая, и, следовательно, проектив-
ные соответствия имеют' одну инвариантную точку, которой и будет
пара (G|,G
2
).
2. Прямая и гиперплоскость пересекаются в точке ABf\DEF = G.
В проективном соответствии (C
1
,D
1
,£
1
,/,...)->(C
2
,A.£
2
,/,...)
ряду (Л
Х
,В
1
,М
1
,...) будет соответствовать ряд (А\ ,В\ ,М\ ,...), а в со-
ответствии (C
]
,D
}
,F
l
,/,...)—>-(C
2
,D
2
,F
2
,l,...) этому же ряду будет со-
ответствовать ряд (А'\,В'\,М'\,...). Ряды (А\,В\,М\,...) и
(Л",, В", ,...) перспективны, так как M'
2
el, М"
2
е1, точка пе-
ресечения рядов (C
l
,D
]
)f] (А
Х
,В
Х
) соответствует точкам на рядах
(А'
2
,В'
2
) и (А"
2
,В"
2
), и соединяющая их прямая пересекает / в
центре перспективности. Поэтому существует точка G
2
пересечения
рядов (А'
2
,В'
2
,М'
2
,...) и (А"
2
,В"
2
, М"
2
,...), которая будет соответ-
ствовать сама себе и будет искомой моделью точки G. Точка
G, е (Л,,В
}
) строится по условию проективности рядов.
3. Плоскость ABC и гиперплоскость DEFG пересекаются по
прямой: ABC(~]DEFG = ML. Для доказательства достаточно дважды
повторить рассуждения предыдущего пункта.
52
2.3. Простейшие аксиоматические модели пространства
Очевидно, что все модели линейной структуры различны по
сложности их графической реализации. Также очевидно, что про-
с гейшей моделью будет та, у которой проективные соотношения за-
менены перспективными. То, что при этом увеличивается число эле-
ментов модели, не сказывается на сложности модели. Поэтому про-
стейшей моделью «-мерного пространства на двумерной плоскости
будет: исключенная точка О, множество прямых, проходящих через
О и несущих (п-1) точек.
Таким образом, модель точки А есть {Л,} с: а, О е a, i = 2, п.
Модель прямой АВ ecxb{A
i
]cia,{B
i
}czb,0&a, Osb,i = 2,n,
l. !../>'.) А
(,!..«,).
i*j,j
= 2^i. _
Модель 2-илоскости А ВС есть {A
t
}аа, \B
i
} <= Ь, {С,- }сс,/'=2,я;
Оеа,ОеЬ,Оес; (А
1
,В
1
)л(А
]
,В
/
), (A
i
,C
I
)A(A
J
,C
J
), (Я„С,)л
л (В,, Сj), i* j, и так далее.
Рассмотрим простейшие графические модели трехмерного проек-
тивного пространства R.. Основным объектом пространства Я, выби-
раем точку. В качестве ее образа выберем пару точек на прямой пучка
прямых с собственной вершиной. Проверим выполнение условия ра-
венства размерностей исходного пространства и его модели. В
соответствии с формулой Грассмана (1.1) размерность множества
точек пространства Р
3
определится следующим образом:
D"' =(3-0)(0 + 1) = 3. Размерность множества пар точек, принадле-
жащих прямым линиям пучка, на основании формулы размерности
многообразия т - плоскостей [5]:
Q=lLa
l
-\m(m + \), (2.3)
/.=о 2
удовлетворяющего обобщенному условию инцидентности
е
'ч'"ч\' «1ао'
0П
Р
е
Д
елится в
символическом представлении следую-
щим образом: Q = Q(e
2
\l) + Q(2e°), где Q(e
2
°
0
)- размерность пучка
прямых, определяемая как <2(<4'о)
=
2-~1-(1 + 1) = 1; Q(2e
]
°)~ раз-
мерность пары точек на прямой пучка, определяемая как
53
Е(2е,°) = 2[1---0-(0 + 1)] = 2. Таким образом Q = 1 + 2 = 3 и условие
равенства размерностей выполнимо.
Рассмотрим выполнение условия соответствия линейности ис-
ходного пространства и его модели. Пространство Р
3
, как точечное
пространство, может быть рассмотрено в качестве грассманова мно-
гообразия. Порядок грассманова многообразия представляет собой
структурную характеристику пространства Р
3
и может быть опреде-
лен на основании формулы [5]:
_ 2\...т\({т + \)(п-т))\
т ко
\
e
n,...,n-m + l,n-m-l) ~ ,
ч|/
,
1Ч
, ,'
e
m,...A,U
(п-т)\уп — т + \)\..м\
следующим образом (при п-3,т-0): (е^У =е*о- Справедливость по-
следнего равенства следует также из его геометрического представ-
ления: е
2
-е
2
'
е
2 "'
Т
Р
И
плоскости пространства Р
2
пересекаются в од-
ной точке. Коэффициент при е% равен 1, что говорит о линейности
пространства Р
3
. Определим структурную характеристику рассматри-
ваемой модели пространства Р
3
. Проведем анализ размерности пар
точек в пучке прямых. Па прямой линии существует двухпараметри-
ческое множество пар точек. В пучке прямых существует трехпара-
метрическое множество пар точек. В центре пучка существует 0 пар
точек. Таким образом, получаем следующее обобщенное условие ин-
цидентности для множества пар точек пучка прямых: е
1
'4"о • Очевидно,
это условие инцидентности, имеющее место для пучка прямых, экви-
валентно обобщенному условию инцидентности для связки плоско-
стей пространства Р
3
. Поскольку пара точек на прямой линии пучка и
точка пространства Р
3
имеют одно и то же параметрическое число,
равное 3, то на основании формулы (2.4) получаем структурную ха-
рактеристику модели пространства Р
3
:
,2,1,0 ,(2+1)(3-2) _ ,2,1,0 ,3 _ 2,1,0 . 2,1,0 _ 2,1,0
V
e
3,2,0/
—
1^3,2,0^
—
^3,1,0
е
3,2,0
—
^2,1,0 '
при этом коэффициент в последнем символическом выражении равен
единице, то есть рассматриваемая модель также является линейной.
Отметим, что полученные структурные условия е\ и е\'\\ являются
единичными. Действительно, в соответствии с формулой (1.4) для
каждого из них получаем:
54
,
0
,_(2-3-0).(0+1)
-2
=
1;
6^.0)
=
,
2X0
(2-3-2).(2 + 1)
3,2,0-* ~
Рассмотрим на простейшей модели пространства Р
3
решения по-
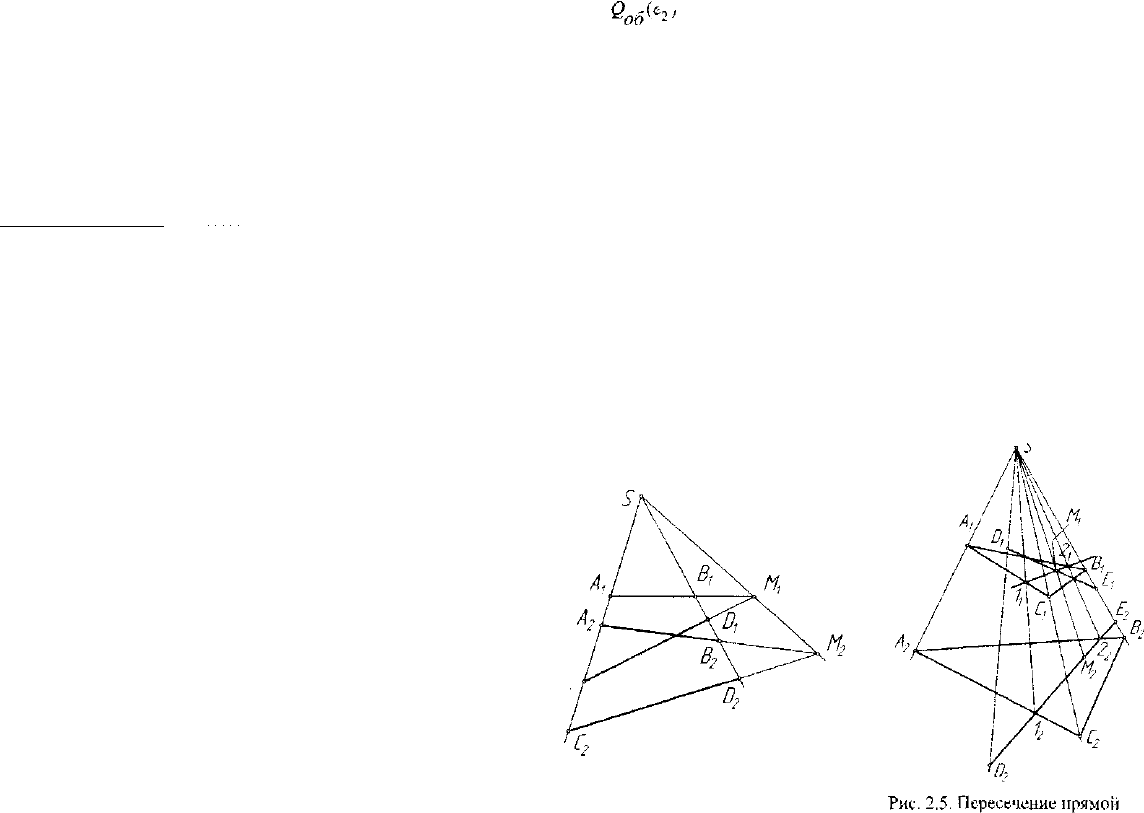
зициотшых задач, например, задач на принадлежность. На рассматри-
ваемой модели (рис. 2.4) заданы пересекающиеся в точке М(М
1
,М
2
)
две прямые линии АВ(А
1
В
1
,А
2
В
2
) и CD(C
]
D
]
,C
2
D
2
). Точка
М(М
Х
,М
2
) принадлежит этой модели, поскольку ее проекции М
х
и
М
2
принадлежат одной прямой пучка (5) прямых. На рисунке 2.5
приведено решение задачи определения точки пересечения прямой
DE и плоскости, заданной треугольником AABC(AA
l
B
l
C
l
,АА
2
В
2
С
2
).
Для этих целей применена конкурирующая прямая 1,2(1|,2,; 1
2
,2
2
) и
соответствующий алгоритм построений. Точка М(М
Х
,М
2
) является
решением задачи.
Выберем в качестве моделируемого аффинное трехмерное про-
странство. Из выбора следует, что возможная графическая модель
пространства должна быть определена как относительно позицион-
ных, так и относительно аффинных задач, то есть задач на параллель-
ность. В таком случае на модели должна быть указана несобственная
прямая, точки которой будут соответствовать несобственным точкам -
v
С,
Рис. 2.4. Модель пересекающихся
прямых
и плоскости
55
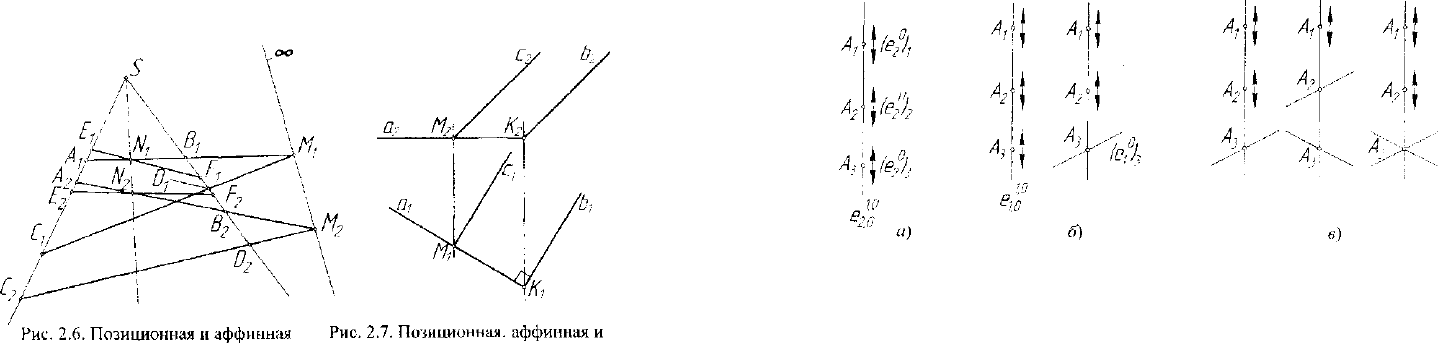
трехмерного аффинного пространства. На рисунке 2.6 приведено ре-
шение двух задач - позиционной и аффинной.
Прямые АВ(А
Х
В
Х
,А
2
В
2
) и EF(E
X
F
X
,E
2
F
2
) пересекаются в точке
N(N
X
,N
2
). Прямые АВ и CD(C
X
D
X
,C
2
D
2
) параллельны, так как их
точка пересечения М(М
Х
,М
2
) принадлежит несобственной прямой -
образу несобственной плоскости аффинного пространства.
Частным отучаем рассматриваемой графической модели является
модель трехмерного евклидова пространства, в котором выполняются
решения задач трех типов: позиционных, аффинных и метрических.
На рисунке 2.7 представлены задачи трех типов.
Прямые а(а
х
,а
2
) и b(b
x
,b
2
) пересекаются в точкеК(К
Х
,К
2
). Пря-
мые с(с
х
,с
2
) и Ъ параллельны. Прямые а и b в пространстве обра-
зуют прямой угол с вершиной в точке К .
задачи метрическая задачи
Обобщим эти модели на «мерное пространство и докажем их
линейность. Для этого представим модель частного вида с исключен-
ной прямой /°°, удаленной в бесконечность и точкой S
x
ef°. Тогда
образ точки АеР" будет множеством A
t
е ал = \,...,п — \,а ZD 5"°.
Символически это можно записать в виде условий:
56
Умножив это условие на единичное п кратное условие, получим
линейное условие нулевой размерности. Единичных «-кратных усло-
вий существует два вида: ((?,')" и el'lief)""
1
.
Получим:
4>2°), •.•••(е°
2
)п->х{е?Г=е
2
№)
1
•...-(,">., ,.(*oV. или
^2), ••..•(e°
2
)
n
_
i
хе^Г
1
-...-(ebV.-
И в том и в другом случае получена модель точки, которая явля-
ется пересечением п гиперплоскостей.
Например, пусть п = 4. Имеем модель точки (рис. 2.8, с/) в виде
1.0 / ,0ч /0
Л
/ 0ч
<?2,o(e
2
)i -(«2)2 '(е
2
)з-
Рис. 2.8. Модель точки пространства^
Если наложить одно линейное условие, т.е. условие принадлеж-
ности точки гиперплоскости, то получим (рис. 2.8, б):
).
•
(4)2
•
(4h или
е
2
>°
0
(е
2
\
-
(е°
2
)
2
•
(е
1
°)
3
.
При наложении двух условий, т.е. условий принадлежности двум
гиперплоскостям, получим (рис. 2.8, в): е\^(е
2
)
[
-(е
2
)
2
-(е
<
]
)
)
3
или
^о(^).
Mh М)ъ и™
е\1(е
й
2
\
.(е°
2
)
2
-{е°
0
)
3
.
И так далее.
57
ГЛАВА 3. МОДЕЛИРОВАНИЕ ТОЧКИ, ПРЯМОЙ,
ПЛОСКОСТИ И ГИПЕРПЛОСКОСТИ НА ПРОСТЕЙШЕЙ
ГРАФИЧЕСКОЙ МОДЕЛИ ЕВКЛИДОВА ПРОСТРАНСТВА
Вышерассмотренная простейшая графическая модель «—мерного
евклидова пространства, полученная аксиоматическим путем, по су-
ществу представляет собой обобщение известной в начертательной
геометрии модели Г. Монжа, которая была получена им конструктив-
ным путем. В проективной схеме метода двух изображений модель
Монжа рассматривается как его частный случай [6, 16J.
3.1. Моделирование точки
X-
ЛгЛз
/7/
и
ZA
О
Точка А на простейшей графической модели представлена своим
образом - «-1 точками А
х
, ...,А
п
_
х
,
принадлежащих одной прямой пучка с
несобственным центром (рис. 3.1). В /л
терминах модели Монжа точки ^
А], ...,А
п
, и прямая А
1
А
п
_
1
называются
соответственно проекциями точки А и
линией проекционной связи. Для мет-
ризации графической модели (то есть
возможности решения метрических за- /А
дач) и ее аналитического описания,
введем в плоскости модели оси коор- I у
динат X, Y,Z,T, где X 1 YZT и
А
}
А
п
, // YZ, и единичный отрезок на
осях, например, 1 мм. В таком случае
появляется возможность задания на рассматриваемой графической
модели декартовых координат точки А и ее проекций:
A(x
A
,y
A
,z
A
,t
A
), A,(x
A
,y
A
,0J)), A
2
(x
A
,0.z
A
,0), А
3
(х
А
. О, 0,t
A
). Отме-
тим, что в соответствии с конструктивным методом основным объек-
том пространства Е, является точка, основными плоскостями проек-
ции служат координатные плоскости: XxZ-lI
2
, X х Y - Я,,
X х z = Я j, а направление проецирования - ортогональное к плоско-
стям проекции (рис. 3.2). Если мысленно убрать основной объект -
точку А и линии проецирования АА
Х
, АА
2
и повернуть горизонталь-
*
Рис. 3.1. Модель точки
пространства Е
п
58
ную плоскость проекции я, относительно оси X до совмещения с
X-
п
2
Z
Z
п
2
'Пз
А
2
г
„
А
з
ZA
УА
п
Y
/7,
Л/
'/А
0
Y
Рис. 3.3. Модель точки
пространства Е
3
Рис. 3.2. Модель Монжа
пространства Е
3
фронтальной плоскостью проекции п
2
, то получим чертеж, пред-
ставленный на рисунке 3.1 (без учета П
3
, A
3
,t
A
nT).
Если ввести профильную плоскость проекции П
3
= Ух'/,, кото-
рой принадлежит ортогональная проекция А. точки А, то получим
дополнительно профильную проекцию A
3
(Q,y
A
,z
A
). После поворота
плоскости // j относительно оси Z до совмещения с плоскостью п
г
образуется чертеж, представ-
6
Х-
п
2
в
2
п,
#7
E
2
=Ei
Пз
О
Y
Рис. 3.4. Модели точек
пространства Е
ъ
, принадлежащих
плоскостям проекций
ленный на рисунке 3.3. Оче-
видно, точка А(х
А
,y
A
,z
A
),
изображенная на чертеже, за-
нимает общее положение в
пространстве относительно
плоскостей проекции п\, Л,
и П
3
, так как ни одна из ее
координат не равна нулю. Ес-
ли же одна из ее координат
равна нулю, то точка принад-
лежит плоскости проекции,
например, точки В(х, у, 0);
С(х, 0,z); D(0,y,z), принад-
лежат плоскостям проекции
59
