Волков В.Я. и др. Курс начертательной геометрии на основе геометрического моделирования

Подождите немного. Документ загружается.

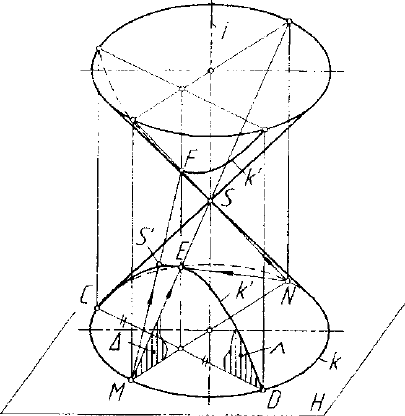
изображение эллипса в плоскости, параллельной плоскости Р, малая

ось которого совпадает с диаметром окружности п'; пара линий - ок-

ружность ri и эллипс с изображением В'

, D'

, принадлежат одному

наклонному цилиндру с образующими, параштельными направлению

s(s

), совпадающему с направлением В'В(В\ В

,В'

), при этом

направление s

совпадает с обратным направлением оси х; прямые

В\ В

и D

D\ - это линии фронтального очерка этого цилиндра. Эл-

липс mczP отображается по направлению проецирования s(s

) на

плоскость 77, в окружность m'(m'

2) с центром 0'(0[,(Х) и диа-

метром l'j.2'

. Учитывая направление s

и наличие линий щ и т\,

строим изображение п\ искомого эллипса т = РГ\Г. Пара точек

(А\,С,) € п\ строится таким образом: (А

= С

) -» (А\ - С

) ->

{т(т

,т

) с Р} -> {m'(m\,iri

) cz с Я,}.

Рассмотрим подробнее геометрический смысл свойства 4 квадри-

ки для удобства последующего его применения в решениях задач на

220

-+{А\,С\)^>(А

,С{).

Очевидно, при вы-

бранных направлении

s проецирующей связ-

ки Ф

2[[>

и плоскости

отображения 77 = /7,,

поверхность 7', пред-

ставляемая как непре-

рывное однопарамет-

рическое множество

подобных и подобно

расположенных эллип-

сов с центром на линии

/(./i>i

)

и в

плоскостях,

параллельных плоско-

сти Р, отображается на

плоскость 77( в непре-

рывное однопарамет-

рическое множество

окружностей с центра-

ми на линии у,, то есть

Рис. 7.12. Перспективное соответствие

кривых второго порядка

пересечение рассматриваемого типа. Пусть на конусе второго порядка

(рис. 7.12), например, на прямом эллиптическом, имеются два раз-

личных конических сечения: одно к - в плоскости И _1_ г, другое к' -

в плоскости ЛИ7, где /' - ось конуса. Для определенности ука-жем,

что к - эллипс, к' - гипербола, причем CD - их общая хорда.

Проведем через середину хорды CD и ось i конуса плоскость А,

которая отсекает на гиперболе к' две точки - ее вершины Е и F, а на

эллипсе к - две точки М и N. Для хорды CD можно указать два

соответствующих ей сопряженных диаметра. Один - ЕЕ, у линии к'

и другой, MN, - у линии к . Напомним, что сопряженность

диаметров есть аффинное свойство кривой второго порядка и состоит

в том, что каждый из сопряженных диаметров делит пополам хорды

кривой, проведенные параллельно другому диаметру. Очевидно,

кривые к и к' являются перспективно соответственными, а вершина

S конуса перспекивности представляет собой точку пересечения

прямых MEf]NF. На рисунке 7.12 дано построение еще одного

центра 5" перспективности линий к и к': S'-NEC\MF. Эта

особенность конических сечений отражена в свойстве 5 квадрики и

может быть использована для решения задач рассматриваемого типа

пересечений. Для определения центра S перспективности

необходимо для кривой второго порядка на квадрике найти

перспективно соответственную ей другую кривую второго порядка

этой квадрики. Затем при помощи двух пар перспективно

соответственных точек этих линий найти центр перспективности,

который представляет собой вершину конуса перспективности. Эта

вершина принимается в качестве центра проецирующей связки

прямых, служащей фактормножеством пространства £

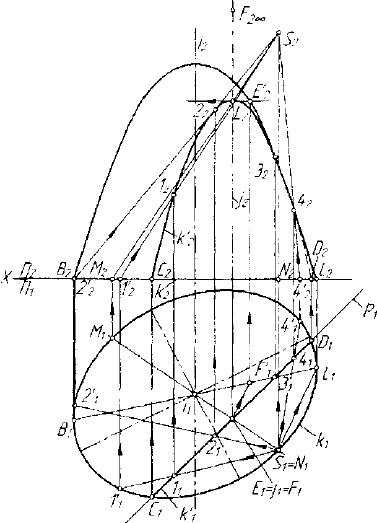
Пусть на графической модели заданы изображения фронтатьного

и горизонтального очерков отсека эллиптического параболоида и след

Р, плоскости Р ±77, (рис. 7.13). Определим сечение поверхности

плоскостью Р. Очевидно, искомым сечением является парабола.

Отрезок С,Д есть горизонтальная проекция К\ искомой параболы.

Построим се фронтальную проекцию к\. Для хорды С

Е\ проведем

соответствующий ей сопряженный диаметр Mj/Vj эллипса к

. Точка

Е\ - C

]

f]M

[

есть горизонтальная проекция вершины Е параболы

. Для построения ее проекции Е\ воспользуемся вышеприведенным

свойством 1 квадрики. В соответствии с ним две параболы в осевых

221

проецирующих плоскостях со следами и M

на плоскости 77]

являются родственными, то есть находятся в перспективном

соответствии с несобственным центром перспективности,

определяемым направлением прямой - направлением родства.

Это родство определено в пространстве Е$ плоскостью родства,

проходящей через ось / перпендикулярно направлению родства,

определяемому прямой NL, и парой родственно соответственных

точек N и L. Поэтому строим вначале прямую Е^Е^/ЩЦ, затем

строим

fs2, где (Е\е

T^TL,)

—» Е\, при

этом

принадлежит фронтальному очерку параболоида, а затем

—>Е

еу

> где прямая j(J],j

) есть ось симметрии параболы к'.

В соответствии с построениями на рисунке 7.12, хорда CD является

общей для соотвествующих ей сопряженных диаметров:

Рис. 7.13. Пример определения пересечения квадрики и плоскости

222

MN(M

]

) эллипса и EF

]

2oo

) параболы

k\k\,к'

), где F

2:0

) - несобственная точка оси симметрии j.

Поэтому точка s

= М

С\Ы

2х

есть фронтальная, а точка s

=N, -

горизонтальная проекции вершины 5 конуса перспективности линий

кик'. Па рисунке 7.13 показаны построения фронтальных проекций

и 4

точек 1, 2, 3 и 4 параболы к' по их горизонтальным

проекциям 1],2],3] и 4, на отрезке C

=k\. Как следует из

приведенного описания решения задачи, центр S(S

) является

центром проецирующей связки Ф

2<|)

, а плоскость П

— плоскостью

отображения. В этом отображении образом параболы к' является

эллипс k(k

,к?).

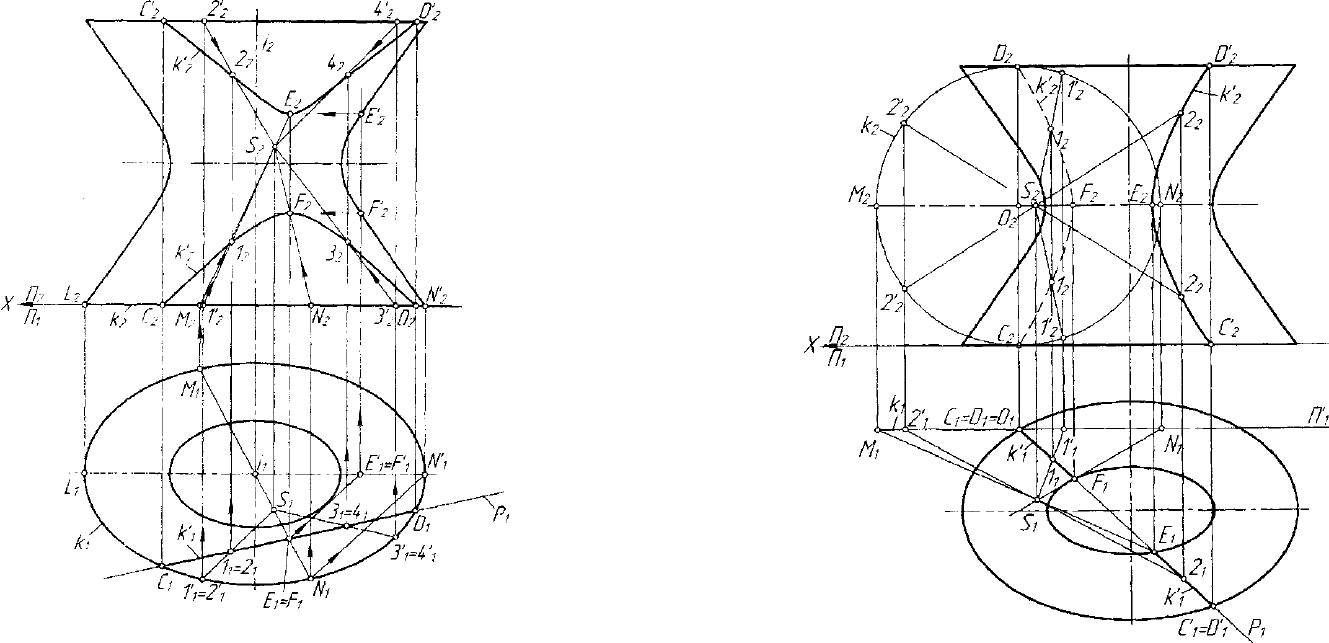
Рассмотрим еще пример. Пусть на графической модели заданы

очерки отсека однополостпого эллиптического гиперболоида Г и

след Р

проецирующей плоскости РА-П

(рис. 7.14). Требуется

построить линию пересечения ГГ]Р. Плоскость Р пересекает

поверхность Г по гиперболе к' с проекцией к\ = С

£\ на плоскости

. Как и в предыдущем примере, принимаем две кривые второго

порядка - эллипс к(к

,к

) и гиперболу к' в качестве перспективно

соответственных линий, у которых сопряженные диаметры

MN(M

) и EF(E

) соответствуют общей хорде

CLKC

E\,C

). Вершины Е(Е

,Е

) и F{F

) искомой гиперболы

к' определены в соответствии со свойством 1 квадрики на основе

родственного соответствия двух гипербол с проекциями Ц№

и M

N-

на горизонтальных следах проецирующих плоскостей, проходящих

через ось / поверхности Г, при этом направление родства

определено прямой ^JV,, то есть родство в пространстве E

определено плоскостью родства, проходящей через ось i поверхности

перпендикулярно прямой NN', и парой соответственных точек N и

/V. Последовательность построений вершин Е и F гиперболы к'

следующая: (Е, = F

)^(E

= F

)^>(E

= F

)-^>(E

). Центр

перспективности S(S

) определяется в соответствии с

построениями на рисунке 7.12 как точка пересечения двух прямых:

223

MEC\NF - S, при этом вначале определяется проекция

= M

f]N

затем S

{

Наличие конуса перспективности (S,k) позволяет построить

проекцию К2 искомой гиперболы сечения по множеству точек ее

проекции /с*,. В рассмотренном примере проецирующая связка Ф

определена вершиной S, а плоскостью отображения служит

плоскость проекций /7,.

Рис. 7.14. Пример определения пересечения квадрики и плоскости

224

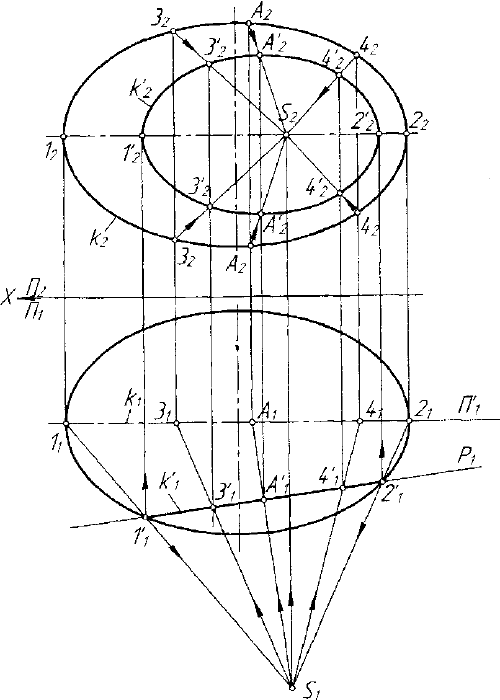
Рассмотрим еще один пример применения свойства 4 квадрики,

в котором одна из кривых второго порядка - окружность, не

принадлежит квадрике. Определим линию пересечения отсека

однополостного эллиптического гиперболоида Г с проецирующей

плоскостью PJ_/7j (рис. 7.15). Очевидно, плоскость Р пересекает

поверхность Г по гиперболе, которая отображается на плоскость Я,

в виде

двух

отрезков

и С\Е

{

. Отрезок СДС7

Д,С

) есть

хорда этой гиперболы. Примем CD в качестве диаметра окружности

&(/Cj,/C2), расположенной для удобства решения задачи в плоскости

777//7

, при этом iTj - горизонтальный след этой плоскости. Две

Рис. 7.15. Пример определения пересечения квадрики и плоскости

225

кривые второго порядка - к (окружность) и к' (гипербола), могут

быть приведены в перспективное соответствие. При этом их общей

хорде CD соответствуют два сопряженных диаметра - один,

MN(M

]

) у окружности к, другой - EF(E

]

) у

гиперболы к'. В таком случае вершина S(S

) конуса

перспективности определяется следующим образом:

NyF^MyNy =S

, S

-^S

e\M

. Конус перспективности (S, к) и

одна проекция к\ гиперболы на нем позволяют построить

недостающую проекцию к\ искомой гиперболы пересечения ГС\Р.

В этой задаче проецирующая связка Ф определена центром 5,

плоскостью отображения служит плоскость уровня 777/77

Воспользуемся теперь свойством 2 квадрики для решения другой

задачи о пересечении рассматриваемого типа. Определим линию

сечения трехосного эллипсоида Г проецирующей плоскостью Р J_ П

(рис. 7.16). Линией сечения РГ\Т является эллипс с проекцией

А.', = I*,2^ на плоскости П

. В соответствии со свойством 2 эллипсы

к(к

,к

) и к' перспективно соответственны. Вершина S(S

) конуса

перспективности может быть определена одним из двух способов в

следующей последовательности: 1,1', П2,2', = S

, S

-> S

е 1

. В

таком случае коническое сечение к' конуса (S,k) в плоскости Р

определеяется по его известной проекции к\ = \\2\ без затруднений.

В данной задаче проецирующая связка Ф

2(1>

определена центром

S, а плоскостью отображения служит плоскость уровня IPIIП

Выясним геометрический смысл свойства 6 квадрики для его

успешного применения в задачах рассматриваемого типа. Каждая

невырожденная квадрика, кроме гиперболического параболоида,

содержит два семейства окружностей. Окружности одного семейства

расположены в пучке параллельных плоскостей. Каждому пучку

плоскостей принадлежат две касательные плоскости (у эллипсоида и

двуполостного гиперболоида) или одна касательная плоскость (у

эллиптического параболоида). Точки касания этих плоскостей с

квадрикой называются омбилическими (точки округления

поверхности). Касательная плоскость в омбилической точке

пересекает квадрику по окружности нулевого радиуса, которая

представляет собой вещественную точку пересечения двух

изотропных прямых этой квадрики. Напомним, что плоскость

226

пересекает конус вращения перпендикулярно его оси по окружности,

радиус которой в вершине конуса принимает нулевое значение, то

есть х

+ у

= О. Откуда следует у - ±ix, i

= -1.

Таким образом сечение конуса рассматриваемого типа в его

вершине представляет собой две изотропные прямые,

пересекающиеся в этой вершине. Любое сечение квадрики

плоскостью А, отличной от пучка параллельных плоскостей,

содержащего касательную плоскость с омбилической точкой 5,

Рис. 7.16. Пример определения пересечения квадрики и плоскости

227

проецируется из точки S на произвольную плоскость 27 этого пучка

в окружность. Действительно, точки пересечения двух изотропных

прямых на поверхности квадрики с плоскостью А проецируется из

точки S на плоскость 27 в две циклические точки, принадлежащие

несобственной прямой плоскости 2\ Следовательно, линия сечения

квадрики в плоскости А, содержащая две точки изотропных прямых,

проецируется на плоскость 2 в линию второго порядка с двумя

циклическими точками. Этой линией является окружность, поскольку

только окружность пересекает несобственную прямую своей

плоскости в двух мнимых точках, которые называются циклическими.

У квадрик вращения два пучка параллельных плоскостей с

окружностями сечений совпадают, при этом плоскости пучка

перпендикулярны оси вращения квадрики. Несобственная точка оси

вращения параболоида служит точкой касания параболоида с

несобственной плоскостью пространства Е^, то есть является

несобственной омбилической точкой. Поэтому эллипсы наклонных

сечений параболоида вращения проецируются на плоскость,

перпендикулярную оси вращения параболоида в окружность.

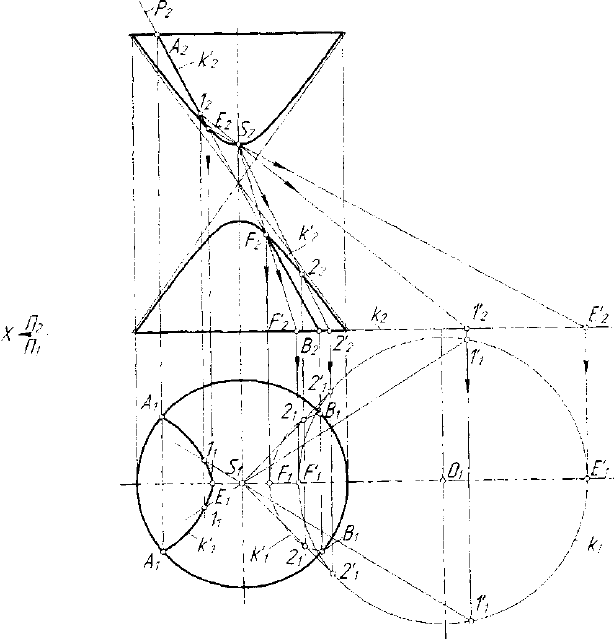
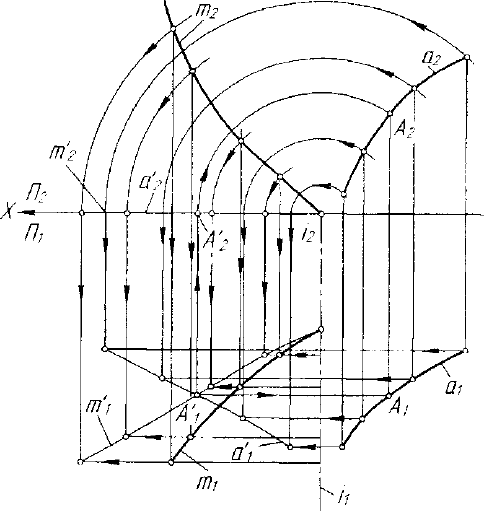
На рисунке 7.17 приведено решение задачи определения линии

пересечения двухполостного гиперболоида вращения Г с

проецирующей плоскостью Р±Л

. Проецирование линии сечения

k' = Pf)r из центра - омбилической точки S(S

) на плоскость /7,

приводит к окружности к(к

), диаметр которой определяется

точками Е'(Е\,Е'

) и F'(F\,F'

), полученными проецированием

вершин Е(Е

1У

) И F(F

) искомой гиперболы из центра S на

плоскость 77j. Наличие конуса перспективности (S.k) и одной

проекции к'

искомой гиперболы позволяет построить другую ее

проекцию к\. В этой задаче проецирующая связка Ф

2(,)

определена

центром S, а плоскостью отображения служит плоскость Я,.

Рассмотрим теперь примеры определения точек пересечения

прямой линии а и квадрики 0. Для этих целей воспользуемся

вышеописанными алгоритмами определения линии пересечения

квадрики плоскостью Р. Смысл и общий алгоритм решений новых

задач на пересечение состоит в следующем. Прямая линия а

заключается в проецирующую относительно плоскостей проекций Я,

или Я

плоскость Р. Очевидно, точки пересечения прямой а и

линии сечения к'= Pf]@ являются точками пересечения af]0. После

228

конструирования центра проецирующей связки Ф

20)

и выбора

плоскости отображения П для целесообразного отображения на нее

компланарных линий а и к', определяем образы искомых точек

пересечения прямой а и квадрики &, как точки пересечения образов

d и к линий а и к'. Точки - прообразы, соответствующие точкам -

образам пересечения a'f]k в построенном отображении, являются

результатом решения задачи. Рассмотрим несколько примеров.

Рис. 7.17. Пример определения пересечения квадрики и плоскости

229

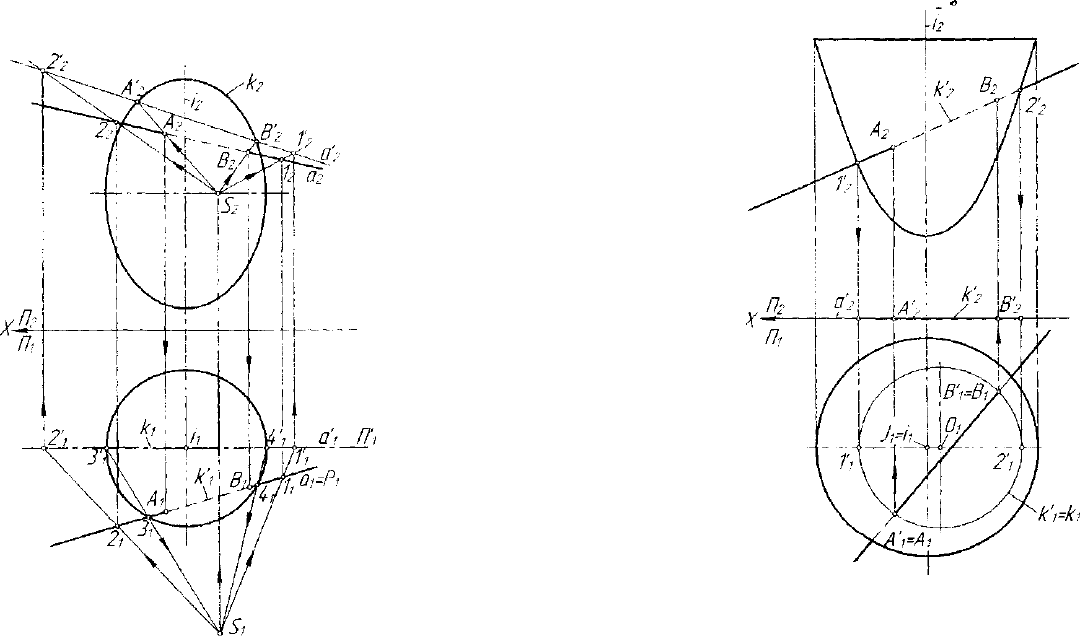
Определим точки пересечения эллипсоида вращения 0 и прямой

линии а (рис. 7.18). В соответствии с предложенным выше алго-

ритмом заключим прямую а в проецирующую плоскость 7*17/,.

Получим а

= Р\ (след проецирующей плоскости Р). Отрезки

34', = А;, и 3,4, = к\ представляют собой вырожденные проекции

двух конических сечений - эллипсов к' и к, где к'=РГ]0, к -

фронтальный очерк квадрики 0. На основании свойства 2 квадрики

определяем вначале проекцию S, =3'

3,П4',4,, а затем S

центра S

проецирующей связки Ф

"'. Отображая этой связкой компланарные

линии к' и а на плоскость отображения 77", которой принадлежит

линия к , получаем образы этих линий: к'—> к(к

,к

), а-*а'(и\,а\).

Рис. 7.18. Пример определения пересечения прямой и квадрики

230

Определяем проекции образов искомых точек a'

f]k

= (А'

,В'

), а

затем и сами прообразы: А\ —» А

еа

, В\ —> В

еа

; А

-» А

е сц,

-> В

еа

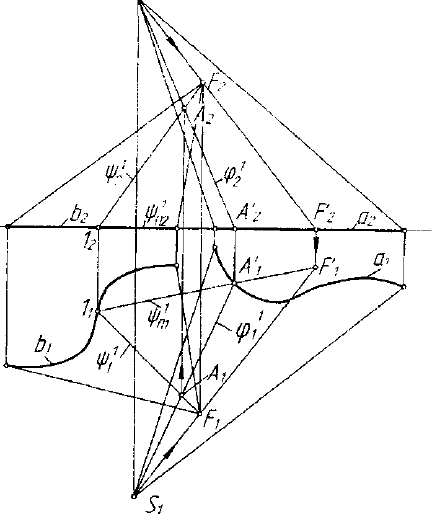
Рассмотрим другой пример. Определим точки пересечения

прямой а и параболоида вращения 0 (рис. 7.19). Решение задачи

выполним на основе использования омбилической точки. Как было

отмечено выше (при пояснении геометрического смысла и значения

омбилической точки),

сечения параболоида

проецирование

вращения ©

=Рг

1=d1

наклонного конического

из его несобственной

омбилической точки (несоб-

ственной точки j

оси вра-

щения /) на плоскость,

перпендикулярную оси вра-

щения i, дает окружность.

В таком случае отображение

компланарных линий аз Р

и к'= Pf\& проецирующей

связкой с несобственным

центром ./^ (У,,./.,,) на оси

; поверхности 0 на плос-

кость отображения п = Я,

дает образы этих линий:

прямую

ЛИНИЮ

а'(а\,а'

) И

окружность к(к

,к

), кото-

рые позволяют получить

искомые точки А(А

{

,А

) И

В{В

.в

) пересечения af) & .

На рисунке 7.20 приве-

дено решение задачи опре-

деления точек пересечения

прямой а и поверхности

эллипсоида вращения © с

этих

осью / _L 77,

Для

целей выбрана проецирую-

щая связка Ф

2(1)

с центром в

Рис. 7.19. Пример определения

пересечения прямой и квадрики

омбилической точке S(S

) и плоскость отображения П-П

Отображение компланарных линий асРи к'=РС\0 на плоскость /7,

231

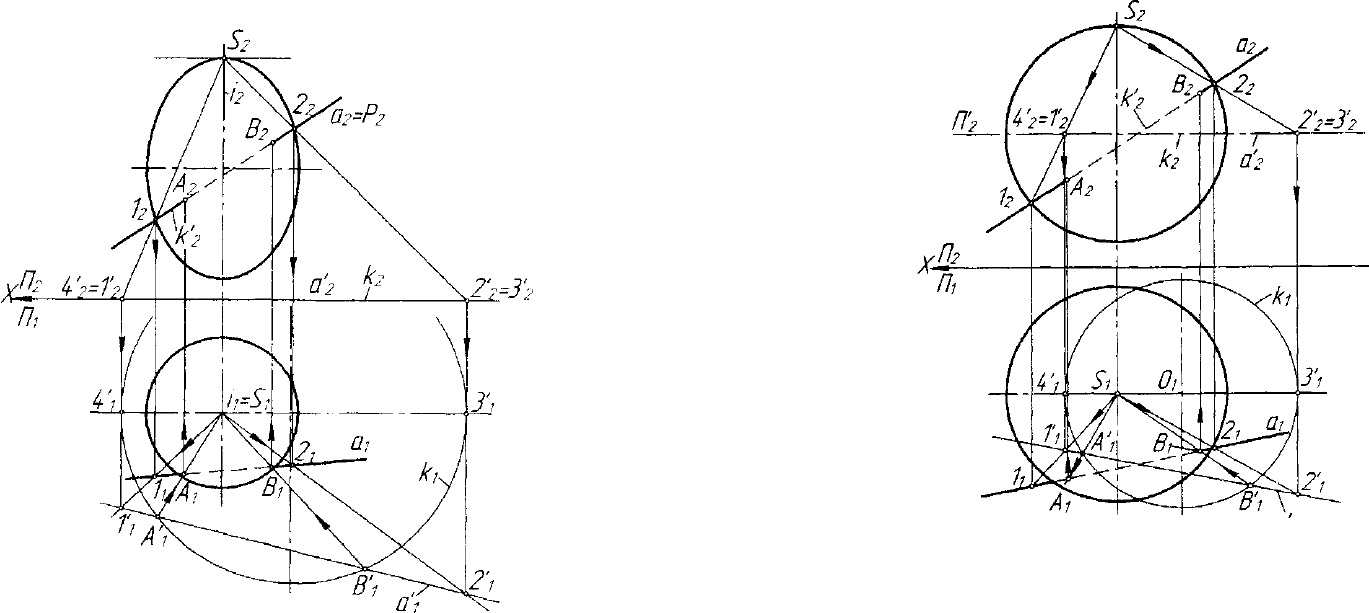
позволяет получить образы этих линий - прямую а'(а\,а'

) и окруж-

ность к(к

{

,к

). Точки пересечения А' и В' этих образов позволяет по-

строить их прообразы А и В в рассматриваемом отображении:

А'-* А(А

), В'-> В(В

). Точки А и В являются результатом

решения задачи.

Рис. 7.20. Пример определения пересечения прямой и квадрики

Т1а рисунке 7.21 приведены построения для определения точек

пересечения прямой а и поверхности сферы 0. Проецирующая

связка Ф

2(и

определена своим центром - омбилической точкой

S(S

) сферы , плоскостью отображения служит плоскость П'IIП,,

проходящая через центр сферы 0. Искомыми являются точки

А(А

) иВ(В,,Я

232

Для всех вышерассмотренных задач на пересечение, в условия,

которых была задана квадрика, решения выполнялись на основе кон-

струирования центра проецирующей связки Ф

2(,)

и выборе некоторой

плоскости отображения.

Рис. 7.21. Пример определения пересечения прямой и квадрики

В некоторых случаях для достижения наибольшей простоты в

построениях удобно применить некоторое линейное преобразование

пространства Ej, в результате которого исходная квадрика преобразу-

ется в квадрику вращения. Пусть, например, заданы эллиптический

параболоид 0, прямая а, и требуется определить точки пересечения

аГ\0 (рис, 7.22). Выполним родственное преобразование простран-

ства £

, в результате которого эллиптический параболоид 0 преобра-

зуется в параболоид вращения & с осью вращения /', которая служи-

ла для поверхности 0 линией центров непрерывного множества эл-

233

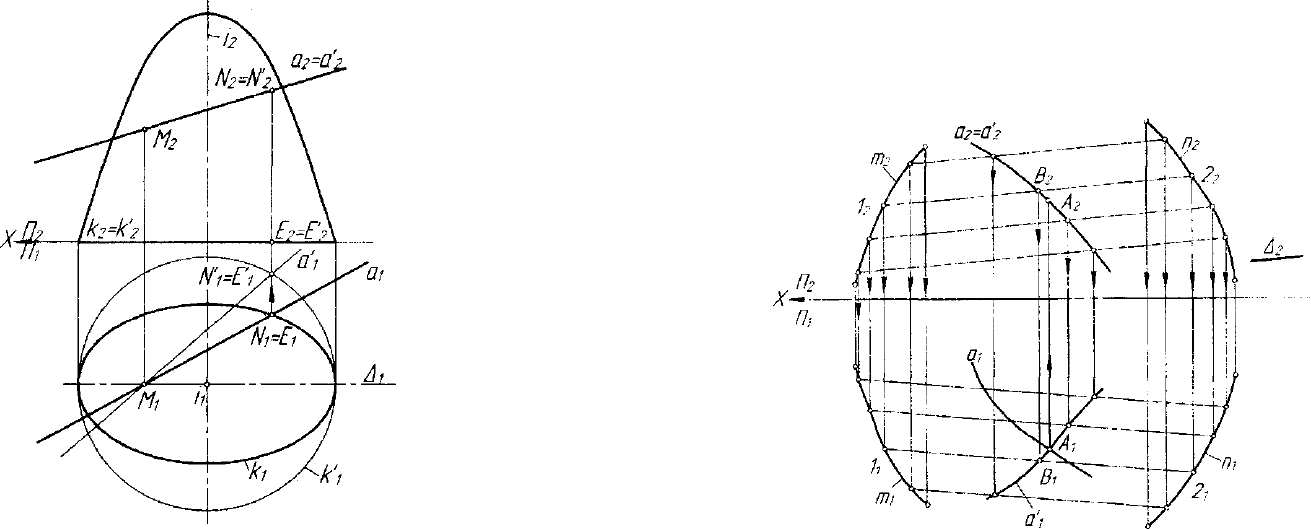
липсов в плоскостях, перпендикулярных линии i. Очевидно, гранич-

ный эллипс

AX^j,^)

отсека параболоида © преобразуется в окруж-

ность к\к\,к\). Введенное родственное преобразование определено

двойной плоскостью АНП

родства, проходящей через ось / поверх-

ности & и парой соответственных в родстве точек E^^EQ) и

Е(Е

,Е

) таких, что ЕЕ' J_ А. Прямой линии «(а,,^) соответствует

ее образ - прямая а'{а\ ,а\ ) во введенном родстве (А,Е,Е').

В результате применения родственного преобразования получаем

Рис. 7.22. Пример применения преобразования (родства)

задачу определения точек пересечения А'Г]&, решение которой было

рассмотрено выше (рис. 7.19). Полученные точки пересечения A'F)@'

являются образами искомых точек в родстве (А,Е,Е). Выполнив по-

234

строения прообразов точек пересечения а'Г\0' в родстве, тем самым

получим искомые точки пересечения af]0.

Рассмотрим применение алгоритма 7.3 для случая линейчатой

поверхности, не являющейся квадрикой. Определим пересечение про-

странственной кривой а и поверхности цилиндроида 0(т,п,А)

(рис. 7.23), у которого линии тип- направляющие линии, плос-

кость A JL П

- плоскость параллелизма. В соответствии с алгорит-

мом 7.3 примем связку проецирующих, относительно плоскости П

прямых в качестве фактормножества пространства

= Е

2{{)

={Jcr

]

. В этом случае заданной линией а выделяется из

связки {Ja

проецирующая поверхность Р(а,П

) = {Jcr

, где <г

]

- про-

2 I

ецирующая относительно п

прямая, пересекающая линию а.

Рис. 7.23. Пример определения пересечения кривой линии и цилиндроида

Линия пересечения а'±(а\,а'

)= РГ]0 есть образ линии а на

поверхности 0 в отображении связкой [ja

. Точка А(Ау,А

) пересе-

235

чения образа d и прообраза а является искомой точкой пересечения

аГ\в.

Рассмотрим пример применения алгоритма 7.4 для случая

поверхности вращения, также не являющейся квадрикой. Определим

пересечение пространственной кривой а и поверхности вращения

@(i,m), где /'(/,,/

) 1 П

~ ось вращения поверхности, т(т

,т

) - ее

образующая линия (рис. 7.24). Для решения задачи в соответствии с

алгоритмом 7.4 примем прямую i в качестве оси нормальной

циклической конгруэнции \Jiy

]

, плоскости окружностей ц/

]

которой

перпендикулярны оси /'. Рассматривая эту конгруэнцию в качестве

Рис. 7.24. Пример определения пересечения кривой линии

и поверхности вращения

проецирующего фактормножества пространства 7%, то есть

= *Р

2(1)

= Uv

' >

принимая плоскость П - П

в качестве плоскости

отображения, строим образ — вырожденное (поскольку поверхность

&(i,m) является проецирующей) отображение т'(т\,т'

)

поверхности 0(i,m) и образ а\а\,а'

) заданной линии а на

плоскости П

{

в этом проецирующем отображении. Точка А\А\,А\)

является образом искомой точки пересечения. Прообраз - точка

А(А

,А

), полученная по схеме А\ -> А

е а,; А'

-> А

е а

, есть

искомый результат решения задачи.

7.4. Алгоритмы конструктивного определения множества

пересечения двух двумерных нелинейных множеств

(поверхностей)

Одной из наиболее сложных в алгоритмическом построении и

конструктивной реализации задач, рассматриваемых в

начертательной геометрии, является задача о построении линии

пересечения двух поверхностей. Для ее решения применяются

различные способы: вспомогательных плоскостей, вспомогательных

поверхностей и др. |2, 15, 20, 22J. Покажем, используя различные

отображения пространства i% на плоскость, что эти способы

являются логическим следствием общего теоретико-множественного

подхода к решению задач на пересечение рассматриваемого типа.

Рассмотрим решения задач на основе применения линейного

фактормножества пространства Е^. Этот подход применяется в тех

случаях, когда одна из двух пересекающихся поверхностей является

конической или цилиндрической. Такая поверхность, представляемая

как линейное однопараметрическое множество Ф

1(1)

=U<p' линейных

классов <р

{

, в соответствии с алгоритмом 7.2, индуцирует

проецирующее фактормножество Ф

2(,)

= [jtp

- Е

. Это

фактормножество представляет собой проецирующую связку прямых

с собственным или несобственным центром - ядром проецирования,

которое исключается из фактормножества. В свете сказанного

покажем применение алгоритма 7.2 для двух пересекающихся

конических поверхностей &(S,а) и Q(F,b), где а(а

,а

) и b(b

)

направляющие линии этих поверхностей (рис. 7.25). Поверхность О

представляем следующим образом: 0 - Ф

ш)

= [)q>

, где tp

]

образующая прямая этой поверхности. Принимая вершину S в

237

236

качестве исключеного ядра проецирующей связки

2(1)

=и^\

пространство Е

представляем проецирующим фактормножеством:

= Ф

2(!)

- U^

. Поверхность Q представляем следующим образом:

О = = U^' , где (//' - образующая прямая этой поверхности.

Примем плоскость П = Я,, которой принадлежит обе линии а и b ,в

качестве плоскости отображения. В таком случае линию а(а

,а

)

можно рассматривать как образ поверхности 6> в ее отображении

связкой U<p' *>а плоскость 11

. Возьмем любую образующую

]

{y\,4/\)czQ и две точки F(F

) и l(l

) на ней. Используя

проецирующую связку, построим образ F'(F

,F'

) точки F на

/7;

Рис. 7.25. Пример определения точки линии пересечения

двух конических поверхностей

238

плоскости Я, : F

-» V\; F\-> F\eS

. Образом точки 1 будет сама

точка. В итоге получаем образ y

iWn\^w\ii)

[

ЯМ0И

принятом

отображении. Точка А'(А\,А'

) = у/

Г]а есть образ искомой точки

пересечения. Сама точка А - проообраз, определяется гак:

А\ -> А

е у/\, А'

-> А

ву/\. Очевидно, образом поверхности Q в

рассматриваемом отображении будет пучок прямых с центром

Рассмотрим еще пример применения в алгоритме 7.2

проецирующего фактормножества пространства Е

представля-

ющего собой связку

2(1)

=и^'

прямых ср . Определим несколько

точек линии персечения конической поверхности 0(S,m) и

поверхности вращения Q(a,t), где mat— соответственно

направляющая и образующая линии, а - ось вращения (рис. 7.26).

Последовательность алгоритмических действий и конструктивных

построений может быть нижеследующей.

1. Поверхность 0 представляем как непрерывное однопарамет-

рическое множество прямых линий: О - Ф

1(1)

= {jcp

, где <р$р\,(р$ -

образующая этой поверхности.

2. Пространство £, "заменяем" фактормножеством £

= Ф

2<1)

= [j(p

, представляющем собой проецирующую связку с исключен-

ным ядром 5(5,,5

3. В качестве плоскости отображения принимаем плоскость

Я = Л,, которой принадлежит направляющая линия Ш поверхности

0. В этом случае образом поверхности 0 в принятом отображении

будет ее направляющая т(т

,т

4. Поверхность Q(a,t) представляем как непрерывное однопара-

метрическое множество W

{Jy/

окружностей у/

(\{/\,уА),

принадлежащих нормальной циклической конгруэнции с осью а .

5. Строим отображение одной из линий - окружности у

на

плоскость 11-у. При этом центр 0(О

) окружности у/ отображается

в точку 0'(0\,0'

), одна из ее точек 1(

) - в точку I'O'i Д'г)-

239