Волков В.Я. и др. Курс начертательной геометрии на основе геометрического моделирования

Подождите немного. Документ загружается.

На основании вышеизложенного рассмотрим вначале моделиро-

вание на плоскости кривой линии пространства Е

5.1. Плоские кривые линии

Из аналитической геометрии известно, что если ввести на плос-

кости декартову систему координат X, Y, то одно уравнение между

текущими координатами точки F(x, у) = 0 в общем случае определя-

ет на плоскости геометрическое множество точек — кривую линию. В

начертательной геометрии, с точки зрения геометрического представ-

ления, кривая линия считается плоской, если все ее точки принадле-

жат плоскости.

5.1.1. Типы точек плоской кривой

Рис. 5.1. Простой отрезок кривой

Для выявления различных типов

точек плоской кривой линии рас-

сматриваются малые ее куски. Про-

стым отрезком кривой линии назы-

вается множество точек, координаты

которых в какой-нибудь декартовой

системе координат удовлетворяют

уравнению у- f(x), где л:, <х<х

При этом х

и х

- фиксированные

граничные значения переменной X;

функция f(x) является однознач-

ной, непрерывной и дифференцируемой [26]. Геометрический смысл

определения простого отрезка кривой ясен из рисунка 5.1. Функция

f(x) определяет взаимно однозначное отображение отрезка [х,,х

]

прямой линии на отрезок [Л,,^] кривой линии. Непрерывность и

дифференцируемость функции f(x) обеспечивают плавный ход кри-

вой линии на отрезке [А

{

,А

], исключающий появление точек само-

пересечения (точка М,) и других особых точек (рис. 5.2). Очевидно,

если поменять "ролями" оси X и Y , то есть рассматривать функцию

х~-<р(у), выполняющую отображение отрезка [урУ^] прямой У на

криволинейный отрезок [А,,А

], то функция х = ср(у) не будет одно-

значной и отображение [.УрУ^] на [А

] не будет биективным.

120

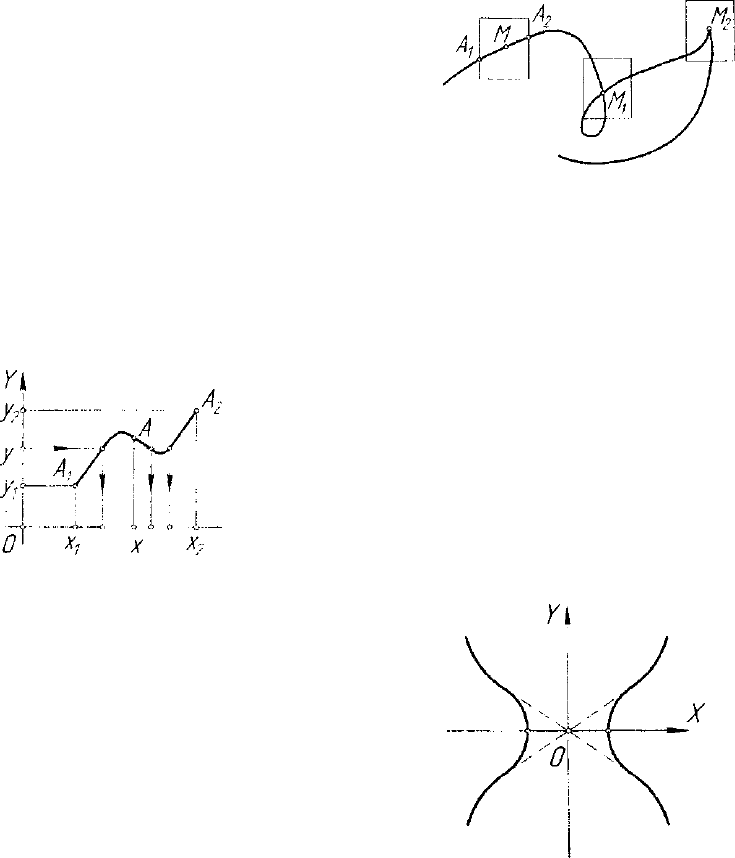
Рис. 5.2. Типы точек кривой

Уравнение F(x,y) = 0, где функ-

ция F(x,y) определена на всей

плоскости или в некоторой ее об-

ласти, определяет кривую линию.

Точка кривой называется обыкно-

венной, если вблизи нее кривая ли-

ния имеет вид простого отрезка, то

есть если точку М кривой можно

заключить в малый прямоугольник,

внутри которого попавшая часть

кривой линии имеет вид простого отрезка. В этом прямоугольнике

уравнение кривой F(x,y) = 0 может быть заменено эквивалентным

ему уравнением y-f(х). Точки, для которых этого добиться нельзя,

называются особыми. Точки М

и М

на рисунке 5.2 являются осо-

быми.

Особые точки кривой линии могут двойными, тройными и т.д.

гонками [26]. Укажем типы и примеры двойных особых точек пло-

ской кривой.

1. Изолированная точка, определяемая как точка самопересече-

ния мнимого продолжения кривой линии. На рисунке 5.3, а) приведен

пример такой точки О для кривой линии у

=-4х +х , а на рисун-

ке 5.3, 6) кривая линия х

+у

=0 состоит из одной изолированной

точки О. В последнем случае кривая линия может иметь следующую

а) б)

Рис. 5.3. Изолированная точка кривой

121

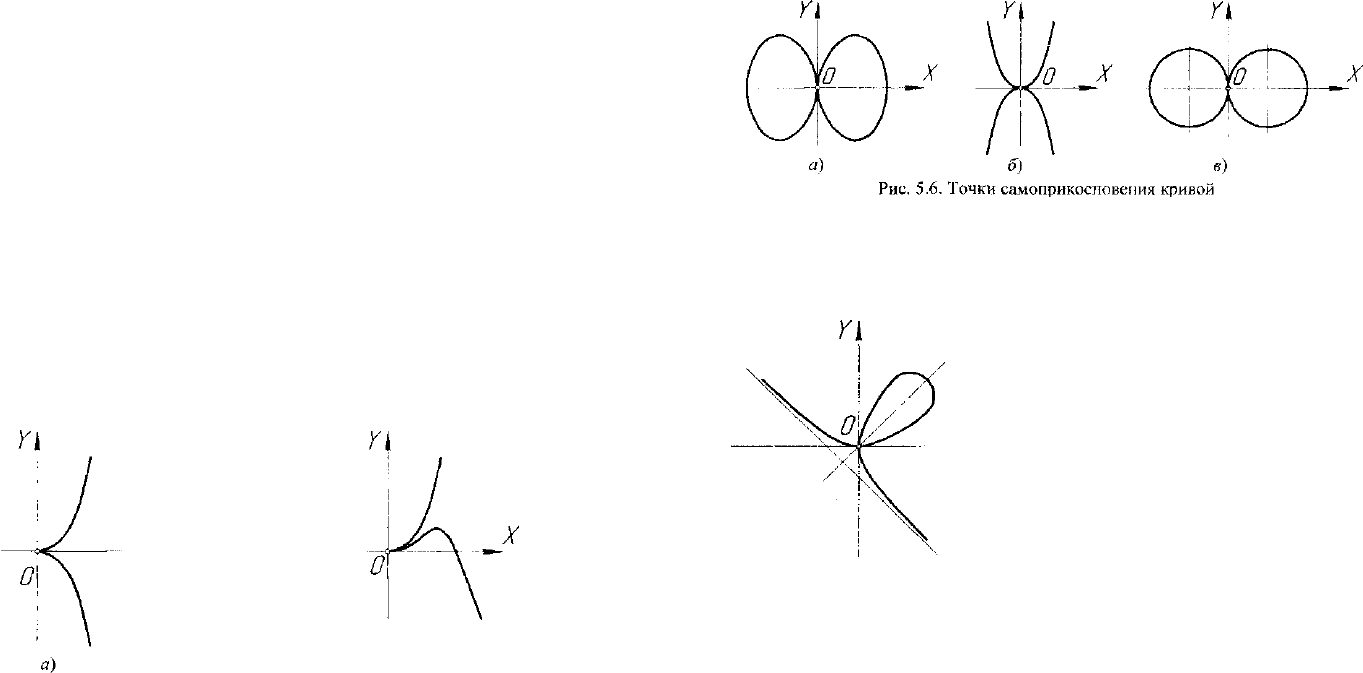
геометрическую интерпретацию - она представляет собой сечение

(нулевая окружность) кругового конуса плоскостью, проходящей че-

рез его вершину. Это сечение представляет собой пару мнимых (изо-

тропных) прямых у = гх и у--ix, где у

= -1, пересекающихся в действи-

тельной точке.

2. Узловая точка, определяемая

как точка самопересечения кривой. На

рисунке 5.4 этому случаю соответству-

ет лемниската Бернулли, имеющая

ОЮ-

2 2 ^ 2 2 2

уравнение (х + у )" -2а (х -у )-0.

Рис. 5.4. Узловая точка кривой

3. Точки возврата или точки заострения. К таким относятся точ-

ки возврата первого рода (рис. 5.5, а)) и точки возврата второго рода

(рис. 5.5, 6)). На первом рисунке изображена полу кубическая парабо-

ла у

-х

=0, на втором - кривая (у-х

)

-х

=0.

б)

Рис. 5.5. Точки возврата кривой

4. Точка самоприкосновения. Такая точка содержится у кривой

+>>

-х

=0 (рис. 5.6, а)), у кривой у

-х

=0, представляющей

собой две касающиеся параболы (рис. 5.6, б)), у кривой, состоящей из

двух касающихся окружностей, и представляющей собой осевое се-

чение поверхности тора, образующая окружность которого касается

оси Y вращения тора (рис. 5.6, в)).

122

В зависимости от вида уравнения, записанного в декартовой сис-

теме координат, кривая линия может быть алгебраической или транс-

цендентной [16]. Нераспадающаяся алгебраическая кривая порядка п

не может

(л-1)-(л-2)

иметь больше

двойных точек [16].

Рис. 5.7. Лист Декарта

Отсюда следует вывод, что кривые

второго порядка не могут иметь осо-

бых точек. Кривая третьего порядка

может иметь только одну двойную

особую точку, например, лист Декар-

та, описываемый уравнением

+у -Ъаху и содержащий особую

точку - точку самопересечения (рис. 5.7).

5.1.2. Элементы дифференциальной геометрии плоской кривой

Известно, что вблизи обыкновенной точки /1

(х

,у

) кривая ли-

ния имеет вид простого отрезка и может быть выражена уравнением

v = /(х). Точка А на простом отрезке кривой определяет ее секущую

с угловым коэффициентом, равным tgcp — ~ , где Дх и Ау - при-

Ах

ращения координат, определяемые точкой А (рис. 5.8). При стремле-

нии точки А с любой стороны к точке А

по кривой секущая t

за-

нимает предельное положение I, которое называется касательной.

123

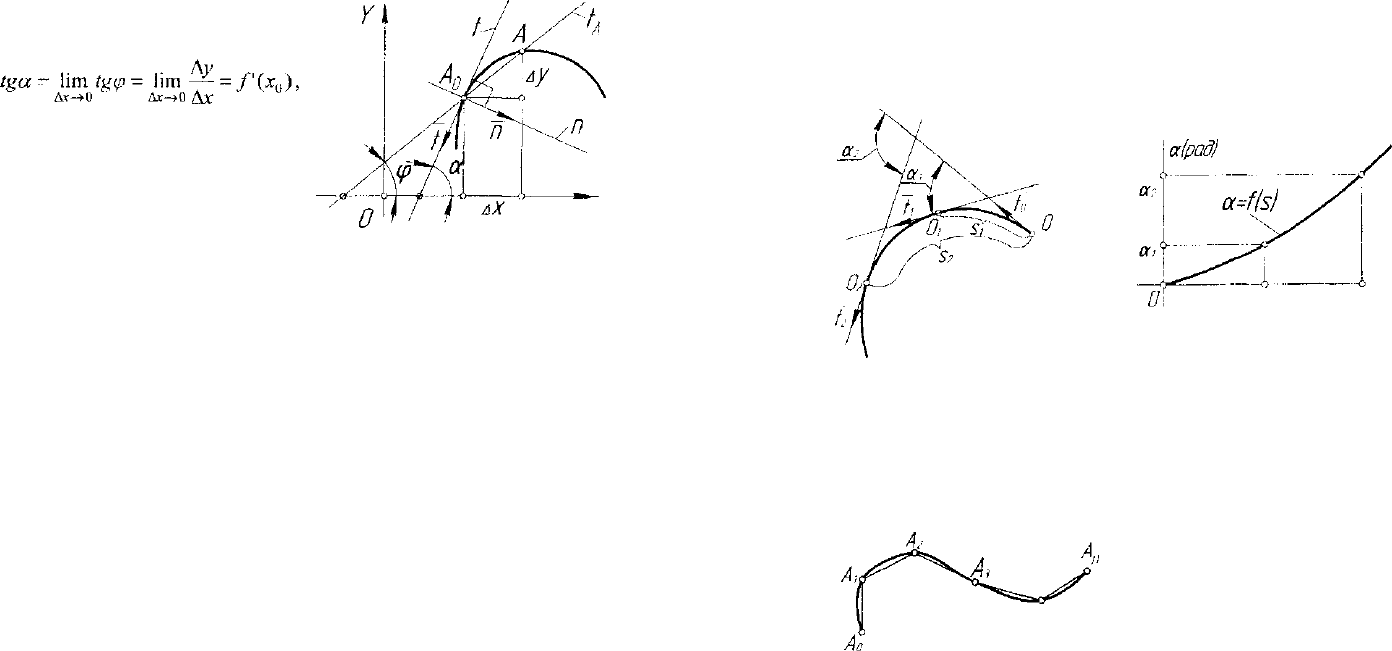
Угловой коэффициент касатель-

ной t в точке А

равен:

где f'(x

) - значение производ-

ной функции f(x) в точке А

Значение углового коэффициента

tga = /'(А'О) в точке А

позволя-

ет записать уравнение касатель-

ной / и нормали и J. t к кривой в

Рис. 5.8. Касательная и нормаль

кривой

ее точке А„: y^y

+f'(x

)-(x-x

) и у = у

- -(х-х

). При

/Ч*о)

этом текущие координаты X и у в первом и во втором уравнении оп-

ределяют положение точки соответственно на касательной и на нор-

мали. Таким образом, в каждой обыкновенной точке плоской кривой

линии существуют единственные касательная и нормаль. Единичные

векторы f и п этих прямых образуют некоторую подвижную ло-

кальную систему декартовых координат с началом в точке А

. Эта

система координат в дифференциальной геометрии называется репе-

ром Френе и имеет важное значение для изучения геометрии плоской

кривой в окрестности ее точки [26J. При смене направления переме-

щения точки вдоль кривой вектор касательной t меняется на проти-

воположный, а вектор нормали п не меняет своего направления.

Отметим, что в рассмотренных выше двойных особых точках кривой

также существуют касательные и нормали.

Если на кривой линии выбрать направление перемещения точки

и начало отсчета О и относительно него определять положение лю-

бой точки Oj кривой линии длиной дуги Sj (расстоянием, измерен-

ным по кривой), а угловое положение касательной t

, определять уг-

лом a

= tj At

(рис. 5.9, а)), то можно представить в декартовой сис-

теме естественных координат а и s (рис. 5.9, б)) график функции

a- f(s), описывающей изменения этих координат по длине дуги

124

кривой [2]. Очевидно, для окружности радиуса R таким графиком

оудет прямая линия a = — s.

О, 0

а) б)

Рис. 5.9. Естественные координаты точки кривой

S(MM)

Рис. 5.10. Длина дуги кривой

Если выбрать на кривой линии множество точек А

, А

, Л,,

, то получим разбиение кривой на множество п кусков кривой, ко-

торое приводит к образованию ломаной линии из п звеньев - хорд

кривой (рис. 5.10). Продолжая про-

цесс бесконечного измельчения

разбиения кривой, мы будем полу-

чать приближение суммы длин

звеньев ломаной, то есть периметр,

к длине кривой от точки А.

до точ-

ки А

. Таким образом, длина дуги кривой есть предел, к которому

стремится периметр ломаной, вписанной в кривую линию, при таком

неограниченном возрастании числа звеньев ломанной, когда длина

наибольшего из звеньев стремиться к нулю.

Как следует из рисунка 5.9, а) при движении точки по кривой

происходит непрерывное изменение величин s (удаление движущей-

ся точки по кривой от ее начального положения) и а (угол поворота

касательной относительно ее начального положения). Степень ис-

кривленности кривой линии характеризуется ее кривизной к , опре-

125

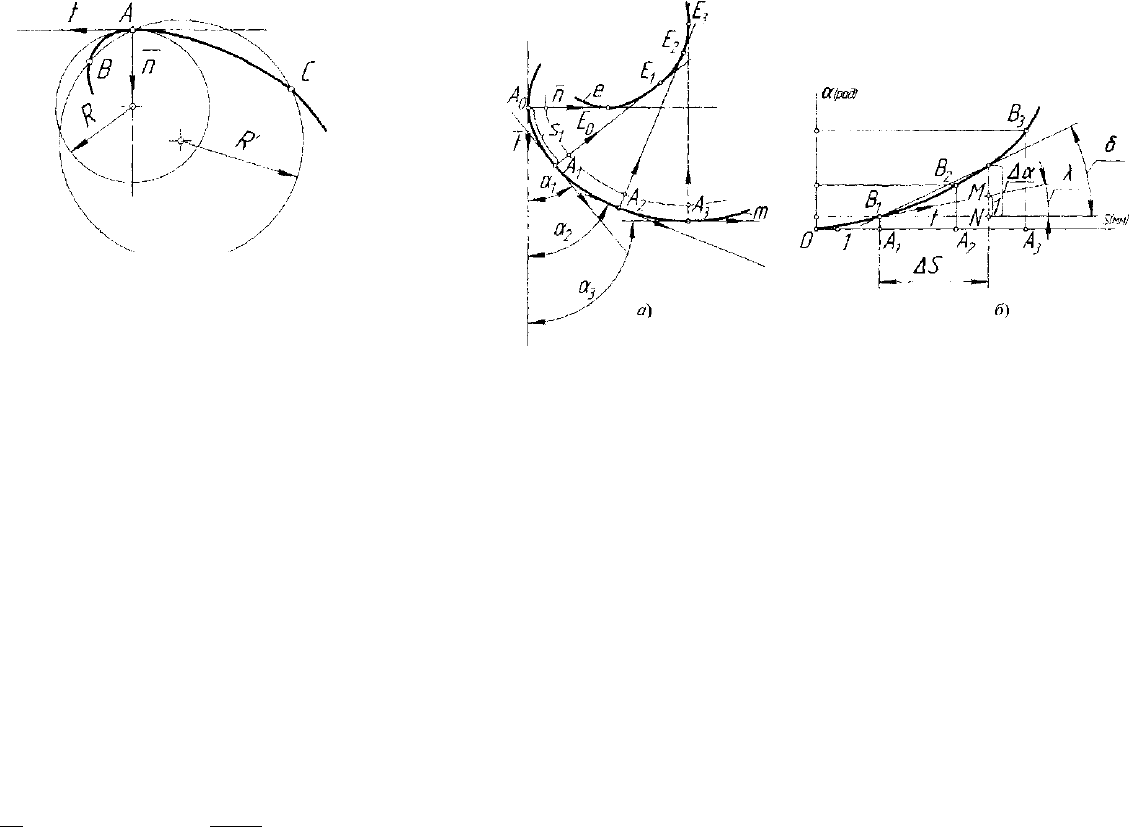
Рис. 5.11. Окружность кривизны

кривой

дсляемой как lim ^—. Величина

л?->о As

R= — называется радиусом кри-

визны кривой в данной ее точке.

Понятие кривизны имеет сле-

дующую геометрическую интер-

претацию (рис. 5.11). Через три

точки А, В и С кривой линии

проведем секущую окружность

некоторого радиуса R'. При

стремлении точек В и С по кри-

вой к совпадению со средней

точкой А окружность R' стремится к своему предельному положению

- окружности радиуса R, при этом R-+R. Предельная окружность

R имеет с кривой в точке А общую касательную с единичным векто-

ром / и общую нормаль с единичным вектором п. Радиус R пре-

дельной касательной окружности называется радиусом кривизны

кривой в ее точке касания с этой окружностью, а сама окружность на-

зывается окружностью кривизны. Взаимное расположение окружно-

сти кривизны и кривой в точке их касания таково, что окружность

кривизны в этой точке одновременно пересекает кривую и касается

ее, то есть имеет место касательное пересечение [26].

Если построить график функции а = f (s) изменения параметров

а и s кривой т, то можно определить кривизну кривой в любой ее

обыкновенной точке (рис. 5.12, а, б). Определим, например, кривизну

кривой в ее точке А

. На графике функции а - f(s) ей соответствует

точка /3,. Проведем в этой точке касательную / к графику. Прира-

щению As параметра S по графику соответствует приращение Лог

^ , MN „ ,. Аа , 1

параметра а. Очевидно, что tgA -----= lira tgd = lim = к = —.

N л*->о

л*->о As R

Следовательно, B

{

N = R-MN. Если принять MN = l (единичный

масштабный отрезок), то R = BjN .

Рис. 5.12. Изменение кривизны кривой линии и эволюта кривой

5.7.3. Эволюта и эвольвента. Касание кривых

Геометрическое место центров кривизны плоской кривой линии

представляет собой кривую линию е, которую называют эволютой

данной кривой т (рис. 5.12, а)). Эволюту определяют также как оги-

бающую нормалей данной кривой. Первоначальная кривая относи-

тельно своей эволюты называется эвольвентой. Из геометрической

схемы образования эволюты следует известное в дифференциальной

геометрии [26, 34] равенство, определяющее взаимосвязь эвольвенты

и эволюты: 77,Е

- R

-R

, где Е

- длина дуги кривой между точ-

ками Е

и Е

эволюты; 7?,, R

- радиусы кривизны эвольвенты т в

се точках Л

{

и А

соответственно. Приведенное равенство может

быть представлено следующим образом: E

= (R

+с)-(Л, + с), где

с - действительное число. Из последнего равенства следует, что, во-

первых, через каждую точку касательной к эволюте проходит единст-

венная эвольвента, во-вторых, для одной и той же эволюты существу-

ет однопараметрическое множество эвольвент. Поскольку касатель-

ные к эвольвентам этого множества в их соответствующих точках

127

126

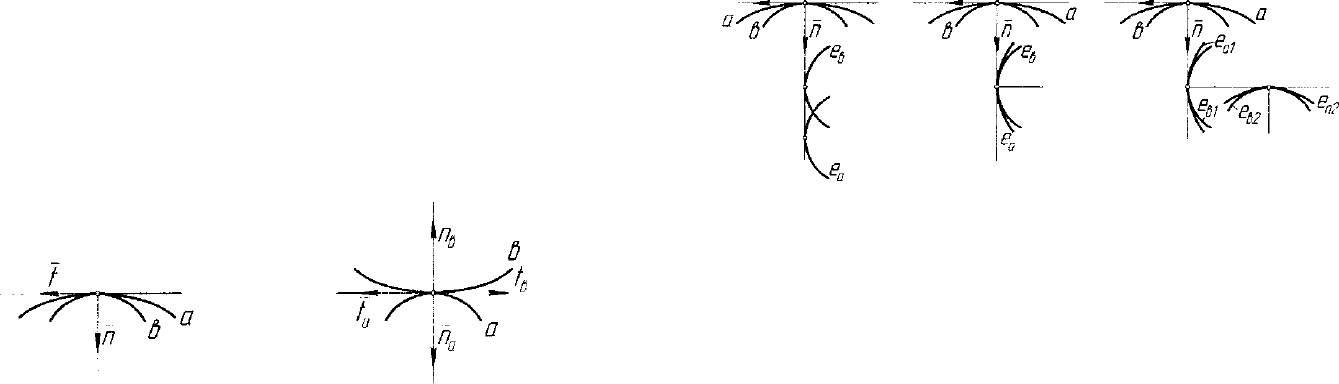
(точках, принадлежащих одной общей нормали эвольвент множества)

параллельны, то эвольвенты множества представляют собой парал-

лельные кривые.

Взаимосвязь геометрий эвольвенты и эволюты позволяет подойти

к важному, с точки зрения теории и практики, понятию касания (со-

прикосновения) кривых линий. Касание двух кривых линий характе-

ризуется наличием у них в общей точке общей касательной и общей

нормали (рис. 5.13).

а) б)

Рис. 5.13. Касание кривых: а) - внутреннее, б) внешнее

Вели у касающихся кривых а и в в их общей обыкновенной

точке имеется только общая касательная, то кривые имеют касание

первого порядка (рис. 5.14, а)), для которого характерно несовпадение

точек касания эволют е

и е

с общей нормалью п линий а и в со-

ответственно.

Если у касающихся кривых а и в в их общей точке совпадают

касательные и их эволюты е

и е

имеют касание первого порядка, то

первоначальные кривые а ж в имеют касание второго порядка, то

есть у них имеются общая касательная в общей точке и один радиус

кривизны (рис. 5.14, б)).

Если у касающихся кривых а и в в их общей точке совпадают

касательные, их эволюты е

а1

и е

в1

первого порядка имеют касание

второго порядка, то есть эволюты е

а2

и е

в2

второго порядка имеют

касание первого порядка, то первоначальные линии айв имеют ка-

сание третьего порядка и т.д. (рис. 5.14, в)).

/ / /

а) б) в)

Рис. 5.14. Порядки касания кривых

Таким образом, если у двух касающихся кривых линий порядок

их касания равен п, то в их общей точке касания первый порядок ка-

сания имеют эволюты (и-1) порядка, второй порядок касания имеют

эволюты (и-2) порядка, (я-1) порядок касания имеют эволюты

первого порядка.

В технике нашли различные применения эвольвенты окружности.

Так, например, профили зубьев колеса и шестерни в зубчатой переда-

че в сечении плоскостью, перпендикулярной их осям, очерчены по

дуге эвольвенты окружности, вследствие чего такая зубчатая переда-

ча называется эвольвентой. Впервые она была предложена Л. Эйле-

ром в 1767 году.

5.1.4. Способы образования ппоских кривых линий

При решении множества различных теоретических и практиче-

ских задач возникает необходимость в получении информации о

форме и геометрии плоской кривой линии, определяемой условиями

задачи. Одна и та же кривая линия может быть определена различны-

ми условиями, каждое из которых выводит на определенный способ

образования (конструирования) этой кривой. Из множества способов,

различающихся теоретическим обоснованием и конструктивной реа-

лизацией, можно выделить основные, наиболее часто применяемые. К

ним относится нижеследующие способы образования кривых линий.

129

128

1. Кривая линия определяется как линия сечения поверхности

плоскостью. Например, кривые второго порядка издревле определя-

лись греками как сечения кругового конуса различными плоскостями.

2. Кривая линия рассматривается как проекция (линейная: цен-

тральная, параллельная, ортогональная, или нелинейная: косая, ок-

ружностная, винтовая и др.) пространственной или плоской кривой

линии на плоскость, например, центральные проекции окружности -

это кривые второго порядка. Кривая может быть рассмотрена как вы-

рожденная проекция (след) поверхности на плоскости, например, ок-

ружностная проекция кругового тора на его осевую плоскость - две

окружности.

3. Кривая линия определяется как геометрическое множество

точек, подчиненных определенному метрическому условию. Напри-

мер, Евклид рассматривай конические сечения (эллипс, гипербола,

парабола) как геометрические места точек, сохраняющихся постоян-

ное отношение расстояний от данной точки (фокуса) и от данной

прямой (директрисы).

4. Кинематический способ. В этом случае плоская кривая рас-

сматривается как траектория движения точки по определенному зако-

ну. Например, циклоидальные кривые представляют собой траекто-

рии точки, жестко связанной с окружностью некоторого круга, кото-

рая катится без скольжения по окружности другого круга. Кинемати-

ческий способ образования кривых был положен Декартом в основу

определения кривых методом координат. В кинематической геомет-

рии изучаются различные кинематические способы образования кри-

вых линий [8].

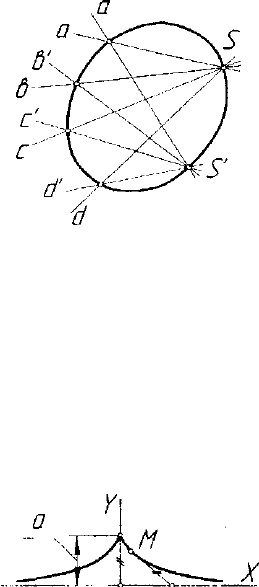
5. Кривая рассматривается как множество точек пересечения

линий двух проективных пучков. Например, в проективной геометрии

известна теорема Штейнера [10, 37], согласно которой кривая второго

порядка представляет собой множество точек пересечения соответст-

вующих прямых двух проективных пучков прямых первого порядка

(рис. 5.15), включая центры пучков. В частности, если угол в паре лу-

чей первого пучка равен углу в паре соответствующих им лучей вто-

рого пучка, то получаем проективное образование окружности, если

при этом вращение лучей в обоих проективных пучках имеет одно

направление. Если вращение разное, то получаем гиперболу [37J.

Кривая третьего порядка, применяемая в синтезе плоских механизмов

[8], определяется как множество точек пересечения соответствующих

элементов двух проективных пучков:

пучка прямых первого порядка и пучка

кривых второго порядка. Два проек-

тивных пучка кривых второго порядка

определяют кривую четвертого поряд-

ка и т.д., то есть кривые высших по-

рядков образуются при помощи проек-

тивных пучков кривых низших поряд-

ков.

6. Кривая определяется заданием

ее дифференциально-геометрических

свойств, то есть свойств, определяю-

щих геометрию кривой в матом. По

условию задачи составляется соотношение между бесконечно маты-

ми элементами линии в виде дифференциального уравнения, после-

дующее интегрирование которого приводит к обычному уравнению

кривой [29]. Например, трактриса представляет' собой кривую, у ко-

торой длина отрезка полукасательной есть постоянная величина а

(рис. 5.16). Изначальное дифференци-

альное уравнение этой кривой имеет

Из

Рис. 5.15. Проективное

образования кривой второго

порядка

вид:

-\\Н~)

]-а

=0.

него

О Р

Рис. 5.16. Трактриса

кривой: х-

а-1п-

•V«

-У

после интегрирования, параметриче-

ской подстановки и исключения пара-

метра получается обычное уравнения

131

130

7. Кривая рассматривается как образ линии в заданном преобра-

зовании плоскости (аффинном, проективном, центральном нелиней-

ном и др.) [16]. Например, в квадратичном преобразовании плоскости

образом прямой линии является кривая второго порядка [8, 16]; обра-

зом окружности в родстве является эллипс [37].

8. Кривая линия представляет собой график некоторой функции,

которая может быть задана аналитически, то есть уравнением. На-

пример, к кривым, которые первоначально определялись уравнения-

ми, относится декартов лист - трафик функции х

+ у

- Заху - О

(рис. 5.7).

5.1.5. Общие свойства плоских алгебраических кривых

Множеству уравнений, связывающих две переменные координа-

ты в декартовой системе координат, соответствует множество пло-

ских кривых. В зависимости от вида уравнения (алгебраическое или

трансцендентное), записанного в декартовой системе координат, кри-

вые подразделяются на алгебраические и трансцендентные. В п. 1.6

было приведено общее уравнение кривой m—vo порядка. В теории

плоских алгебраических кривых [16, 29] известны теоремы, опреде-

ляющие общие свойства этих кривых. Приведем основные из них.

1. Порядок алгебраической кривой не зависит от положения

этой кривой относительно системы координат. Действительно. Урав-

нения преобразования системы координат, описывающих комбина-

цию поворота и параллельного переноса, имеют вид:

х = а

+ b

+ с,; у = а

+ Ь

+с

, где X, у и х

- соответст-

венно старые и новые координаты. Подстановка этих линейных урав-

нений в общее уравнение плоской алгебраической кривой (п. 1.6) не

увеличивает и не уменьшает степень этого уравнения.

2. Алгебраическая кривая т-то порядка определяется заданием

m(m

ее точек. Несложное доказательство этого утверждения

представлено в п. 1.6.

132

3. Две неприводимые алгебраические кривые порядков от, и т

пересекаются не более чем в от,-от

точках. Приводимой считается

кривая, левая часть уравнения которой может быть представлена в

виде произведения алгебраических функций f

(x,y)• f

(x,у)•... = 0.

В таком случае кривая представляется системой линий: f

(x,y) = 0,

(

, у) = 0, ... В основу доказательства приведенной теоремы поло-

жена известная в алгебре теорема о числе корней системы из двух ал-

гебраических уравнений степени т

и т

. Если одна из линий явля-

ется прямой, например, т

-\, то от,-от

=от,, и порядок плоской

кривой представляет собой число точек се пересечения с прямой в

плоскости кривой.

4. / -кратная точка алгебраической кривой эквивалентна зада-

нию —~—- простых ее точек. Помещая начало декартовой системы

координат в t -кратную точку, мы тем самым превращаем общее

уравнение кривой (п. 1.6) т-го порядка в уравнение без последних t

строк, поскольку только в этом случае t -кратная точка (х - 0,у = 0)

будет превращать t раз уравнение кривой в тождество ОеО. Оче-

t-(t + l)

видно, количество коэффициентов в этих t строках равно —- • - - .

Применительно к кривой 3-го порядка можно сделать вывод о том,

что определяемая девятью простыми точками, она может быть опре-

делена также одной двойной и шестью простыми точками.

5. У неприводимой алгебраической кривой от-ro порядка может

(w-l)-(w-2) „ _ .

быть не более -- двойных точек. Если бы кривая имела,

(т-\)-(т-2) ,

предположим, —- ~ - + I двойных точек, то через эти точки и

(т - 3) других точек этой кривой можно было бы провести, на осно-

вании теоремы 2, другую алгебраическую кривую (от-2) порядка.

^ (от-1)-(от-2)

Это следует из того, что сумма точек \-\ + (т — 3) =

133

(m-2)-(m + i)

определяет по теореме 2 кривую линию (ли - 2) по-

рядка. Но поскольку каждая двойная точка первой кривой считается

как две точки ее пересечения с другой кривой, то получаем число то-

= т • (т - 2) + ], что противоречит тому, что у кривых порядков т и

(т - 2) число общих точек по теореме 3 равно т-{т-2).

Алгебраические кривые классифицируются не только по их по-

рядку, но и по классу и роду (жанру). Класс алгебраической кривой

определяется степенью ее уравнения в тангенциальных координатах.

Пусть линия f(x,у) = 0 пересечена прямой u-x + v-y + \ = 0. Условие

совпадения двух точек ее пересечения с кривой, записанное в виде

равенства, связывающего коэффициенты и и V, приводит к уравне-

нию кривой в тангенциальных координатах U и V. Например, исклю-

чая из уравнений окружности х

+у

-1 = 0 и прямой u-x + v- у +

+ 1 = 0координату у , получим (и

)x* +2ux + (\-v

) - 0. Условие

касания прямой и окружности представляет собой равенство корней

этого квадратного уравнения, что приводит к равенству

v • (1 - и" - v ) - 0. Если выполнить исключение координаты х, то по

аналогичной схеме получим и

• (1 -и

- v

) = 0. Очевидно, в обоих

случаях имеет место условие 1-гг -v

=0, которое и представляет

собой тангенциальное уравнение окружности. Геометрически класс

плоской кривой определяется числом касательных к кривой линии,

проведенных из точки вне кривой. Порядок т и класс к плоской ат-

гебраической кривой в общем случае не совпадают, лишь в случае

кривой второго порядка имеет место т = к. Если принять обозначе-

ния: т - порядок кривой, к - класс кривой, d - число двойных то-

чек (узловых и изолированных), г - число точек возврата, t - число

двойных касательных (прямых, касающихся кривой в двух точках), w

- число точек перегиба, то между этими числовыми характеристика-

чек пересечения двух кривых, равное 2 • [

(т-1)-(т- 2)

+ 1] + (|и-3) =

134

ми можно установить следующие соотношения, так называемые фор-

мулы Плюккера, полученные им в 1834 году:

•

(т -1) - 2d - Зг; т = к

•

(к -1) - 2/ - 3w;

w = Зт

•

(т - 2) - 6d - 8r

;

г = Зк

•

(к - 2) - Ы - 8w.

Род или жанр алгебраической кривой равен числу р, представ-

ляющим собой разность между наибольшим числом двойных точек,

которые могут быть у кривой порядка W, и их фактическим числом у

данной кривой. Род определяется следующим образом:

(m-l)-(

^)_

Jk-l).(k-2)_

2 2

Если кривая линия содержит наибольшее число двойных точек,

возможных для кривой данного порядка, то она называется рацио-

нальной (кривая нулевого рода). Кривые этого типа обладают сле-

дующим важным свойством: координаты точки, совершающей пере-

мещение по такой кривой, могут быть выражены рациональными

функциями некоторого параметра.

Важное теоретическое и практическое значение имеют цирку-

лярные кривые. Если в уравнение окружности (х-а)~ +{у-Ь)

- R

= 0 подставить координаты х - у = ~

-, где х

{

,х

- одно-

родные декартовы координаты, то получим уравнение

(х, -ах

)

+(x

-bx

)

-R

=0. Решая его совместно с уравнени-

ем несобственной прямой х

= 0 плоскости этой кривой, получим

точки: J, (1, /, 0) и J

(1, - с, 0), где г

= -1. Очевидно, координаты этих

точек не зависят от коэффициентов в уравнении окружности. Поэто-

му можно ут верждать, что любая окружность в плоскости пересекает

ее несобственную прямую в двух мнимых точках, которые назы-

ваются циклическими. Алгебраические кривые, проходящие через

циклические точки, называются циркулярными. К циркулярным

относятся кривая Бурместера, характеризуемая уравнением

(х

+ у

)-(тх + 1у)~1тху = 0. Если в это уравнение ввести однород-

135

ные координаты х = —, У-~,

то

получим уравнение

х, х

(х,

+ х

) • (/их, + /х

) - 1тх

• х

= 0. Если в нем положить х

- 0,

— -к, то приходим к уравнению, из которого можно получить к:

(1 + к )-(Ы + т) = 0. Из уравнения следует: к, =i, к

=-i, к

=—

Следовательно, кривая Бурместера является циркулярной кривой. По-

скольку она третьего порядка, то в пересечении с окружностью обра-

зует шесть точек, из которых две точки - циклические, а четыре точки

- вещественные. Кривые второго порядка могут быть получены цен-

тральным проецированием окружности на соответствующую каждой

кривой плоскость. Центральным проецированием определенного се-

мейства циркулярных кривых m-го порядка на плоскость также

можно получить любую кривую т-го порядка. Рациональные цирку-

лярные кривые нашли множественные практические применения. Па-

пример, кривая Бурместера - в теории синтеза плоских механизмов,

лемниската Бернулли - в профилировании лопаток турбин, теорети-

ческие профили Жуковского, Чаплыгина в авиастроении и др.

В завершении обзора способов образования плоских кривых от-

метим, что мир этих кривых бесконечно велик [29]. Гак, например,

известно более 70 видов алгебраических кривых третьего порядка.

Классификация кривых четвертого порядка связана с именем Варинга

(1792 г.) и насчитывает 84551 кривых частных видов. Алгебраические

кривые более высоких порядков изучены недостаточно и не имеют

сколь-нибудь законченной их классификации. Многообразие плоских

трансцендентных кривых также велико [29], но оно менее изучено в

геометрии, по сравнению с алгебраическими кривыми, ввиду сложно-

сти их геометрической природы. Если исследования метрических

свойств (кривизна, квадратура, спрямление) у трансцендентных кри-

вых выполнены достаточно основательно, то, например, проективные

свойства этих линий не изучены. Нет достаточно удовлетворительной

классификации трансцендентных кривых линий.

136

5.1.6. Кинематическая геометрия плоских кривых

Рассмотрим подробнее упомянутый ранее кинематический спо-

соб образования плоских кривых. В основу одного из применяемых в

начертательной геометрии методов преобразований - метода плоско-

параллельного перемещения, положено предложение о том, что вся-

кое перемещение плоской фигуры в ее плоскости из одного конечного

положения в другое конечное положение может быть достигнуто по-

воротом фигуры относительно некоторого центра в этой плоскости.

Это предложение имеет место и для бесконечно малого перемещения

плоской фигуры в ее плоскости. В этом случае траекторией любой

точки плоской фигуры является бесконечно малая дуга окружности и

с точностью первого порядка малости бесконечно малое перемещение

этой точки может быть заменено перемещением по касательной к

бесконечно малой дуге, а перпендикуляр к касательной в этой точке

занимает положение нормали. Точка пересечения подобных норма-

лей, каждая их которых определяется траекторией мгновенного пере-

мещения соответствующей точки плоской фигуры при ее мгновенном

плоскопараллельном перемещении, является мгновенным центром

вращения плоской фигуры. Множество мгновенных центров враще-

ния плоской фигуры в неподвижной декартовой системе координат в

плоскости фигуры представляет собой кривую - неподвижную цен-

троиду движения плоской фигуры. Множество мгновенных центров

вращения в подвижной системе декартовых координат, неизменно

связанной с подвижной плоской фигурой, представляет собой под-

вижную центроиду. Точка, неизменно связанная с фигурой, совер-

шающей непрерывное плоскопараллельное перемещение, описывает

некоторую плоскую кривую. Эту кривую можно рассматривать также

как образованную той же точкой, неизменно связанной с подвижной

центроидой, при качении без скольжения последней по неподвижной

центроиде. Кривые описанной кинематической схемы образования

называются рулеттами [2, 8].

137

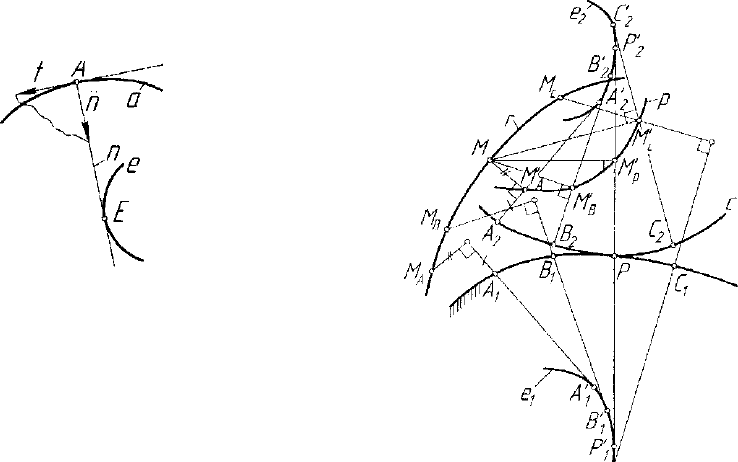
В свете сказанного рассмотрим в качестве примера кинематиче-

ское образование эволюты плоской кривой (рис. 5.17). В каждой

обыкновенной точке А кривой а су-

ществует репер Френе, образованный

единичными векторами касательной t

и нормали п. Рассматривая репер как

плоскую фигуру, совершающую не-

прерывное плоскопараллельнос пере-

мещение при движении его вершины

А вдоль линии а, на основании вы-

шеизложенного можно сделать вывод о Рис. 5.17. Эволюта -

том, что мгновенным центром враще- неподвижная центроида

ния репера при смещении его из точки А служит точка Е эволюты е

кривой О.. Следовательно, неподвижной центроидой непрерывного

плоскопараллельного перемещения репера кривой служит ее эволюта.

Очевидно, подвижной центроидой движения репера служит нормаль-

ная прямая п. В таком случае кривая линия а представляет собой

траекторию движения точки А, неизменно принадлежащей прямой

линии т?, когда, последняя обкатывает кривую е, то есть линия а есть

рулетта точки А, принадлежащей подвижной центроиде п, обкаты-

вающей неподвижную центроиду е. Это как раз соответствует ранее

изложенному кинематическому образованию эвольвенты а по ее

эволюте е.

Рассмотрим образование рулетты. Для получения рулетты необ-

ходимо, как следует из вышесказанного, задать неподвижную цен-

троиду с

, подвижную центроиду с

и точку М, образующую рулет-

ту. Точка М неизменно связана с подвижной центроидой с

(рис. 5.18). Центроиду с

представим как дискретный ряд точек

, В

, Р,С

,..., которому отвечает по условию равенства длин соот-

ветствующих дуг центроид с

и с

ряд точек

,В

,Р,

,...,

то

есть = А$

, В

1*=Ё

1Р,Рс:

=РС

, ...

138

Для каждого ряда точек

на линиях с

и с

проведем

их нормали, огибающими

которых являются эволюты

и е

. Из точки М опус-

-2

тим перпендикуляр на нор-

мали центроиды с

, осно-

вания которых М'

,М'

М'р , М'

, ... принадлежат

линии р подере эволюты

. На нормалях неподвиж-

ной центроиды с*| отложим

отрезки, измеренные на со-

ответствующих нормалях

подвижной центроиды с

' между линиями р и с

, за-

тем к полученным точкам

добавим под прямым углом

Рис. 5.18. Схема образования рулетга отрезки соответствующих

перпендикуляров, измерен-

ные от точки М до оснований построенных перпендикуляров к нор-

малям центроиды с

. Множество полученных точек принадлежит ру-

летте г. Очевидно, по характеру построения рулетга г принадлежит

неподвижной плоскости центроиды с

{

Рассмотрим теперь вопрос определения кривизны рулетты. Пусть

точка М образует рулетту г при качении подвижной центроиды с

по неподвижной с

(рис. 5.19). Пусть точка М

е г бесконечно близ-

ко расположена к начальной точке М е г и ей соответствуют точки

.4, е с, и А

е с

касания центроид с

и с

, бесконечно близко распо-

ложенные к начальной точке Р касания центроид. Введем обозначе-

ния углов: а = п

л п

- угол между нормалью п

рулетты г, про-

139