Волков В.Я. и др. Курс начертательной геометрии на основе геометрического моделирования

Подождите немного. Документ загружается.

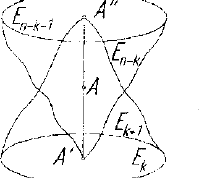
подпространство Е

в Е

есть однозначное отображение точек А е Е

на точки А'е Е

, осуществляемое к -мерным

(А--параметрическим) множеством подпро-

странств Е

, принадлежащих заданному

подпространству Е

кл

Первое, что необходимо отметить, это то,

что это отображение не взаимно однознач-

ное. Действительно, выбрав произвольно об-

раз А'е Е

, получим проецирующее подпро-

странство Е

, любая точка которого, не Рис. 1.12. Операция

принадлежащая Е

}

, может служить про- проецирования

образом точки Л.

пространстве Е„

Второе, что необходимо учесть, это то, что не все точки про-

странства Е

имеют образы в подпространстве Е

. Так, точки

А е Е

не имеют образов на Е

Третье обстоятельство заключается в том, что если рассматривать

графические модели, которые составляют предмет изучения начерта-

тельной геометрии, то необходимо ограничиваться размерностью

пространства образов, то есть необходимо принять к. = 2.

Рассмотрим в общем виде некоторые свойства операции проеци-

рования в пространстве Е

. Рассмотрим проецирование из Е

пря-

мой АВ и точечного ряда А, В, С... на ней. Пусть АВпЕ

= 0. То-

гда линейным расширением < АВ, Е

> является Е

п Е

= Е

- А' #'. В дальнейшем плоскость проекций всегда бу-

дем обозначать /7

, а (п - 3)-мерный центр проекций как S

. Таким

образом, АВ -> А'В'с П

. Проецирующую (и 2)-плоскость будем

обозначать Р

п 2

. Тогда отображение А —» А'е П

будет выполняться

проецирующей (п- 2) -плоскостью -Р„1

, 5->5'е77

- проецирую-

щей (и 2) плоскостью Р„-2- И

так

Далее. Следовательно, точечный

ряд А, В,С,... прямой АВ проецируется пучком (и- 2)-плоскостей

Р,?-2,

Pn-2' К-2'

•••

центром S

в точечный ряд

А\В\С\...

пря-

мой А'В'.

Если окажется, что АВ n S„_

= S

, то проекция всей прямой АВ

на П

будет точкой.

Аналогичными рассуждениями можно показать, что проек-

цией плоскости АВСсЕ

, ABCC\S

=0, является плоскость

А'В'С'=П

. Если же ABCr\S

, то проекцией плоскости ABC

будет прямая, так как <АВС, S„_

> = Р„

и Р

_, п П

- //,. В этом

случае, тоже нарушается однозначность обратного отображения, ибо

прообразом любой точки на П

будет прямая плоскости ABC, прохо-

дящая через S

. Если ABCr\S

= S,, то проекцией плоскости ABC,

будет точка, так как <ABC,S

> = Р

и P

п Я

= П

. Однознач-

ности обратного отображения нет, так как прообразом точки Я

е 17

будет вся плоскость ABC .

Что касается подпространств Е

,Е

,... с: Е

, то в самом общем

случае можно утверждать, что их проекциями на П

будет вся плос-

кость П

и что обратное отображение будет неоднозначным. Дейст-

вительно, пусть даны: Е

с Е„, Е

r)S

. Точка S

не имеет об-

раза на П

. Для любой другой точки А&Е

существует образ

А'еПт. Но проецирующая точку А плоскость имеет размерность

(л - 2) и, следовательно, пересекается с Е

по прямой. Поэтому про-

образом точки А' е П

будет прямая A'S

а Е

Если Е

r\S

_, = 5,, то проекцией Е

на П

будет прямая, а про-

образом каждой точки А' этой прямой будет 2-плоскость

<A',S

>c:E

Если Е

- S

, то проекцией Е

на П

будет одна точка А',

а ее прообразом будет вся 3-плоскость Е

. И так далее.

Все рассмотренные выше операции проецирования можно на-

звать центральными, имея в виду S„_

как (и - 3)-мерный центр про-

ецирования. Известно, что я-мерное пространство имеет бесконечно

удаленную гиперплоскость Е™

. Следовательно, центр S„

можно

целиком погрузить в Е™

{

, удалив его в бесконечность (сделать не-

собственным) и обозначив как S™_

. Задать такой несобственный

центр проецирования можно собственной (п - 2)-плоскостью, кото-

рая пересечет П

в точке. Следовательно, можно на П

выбрать про-

извольную точку и задать в ней (п - 2) различных прямых, направле-

ния которых будут определять положение несобственного центра

5,7-з • Операция проецирования станет параллельной. При параллель-

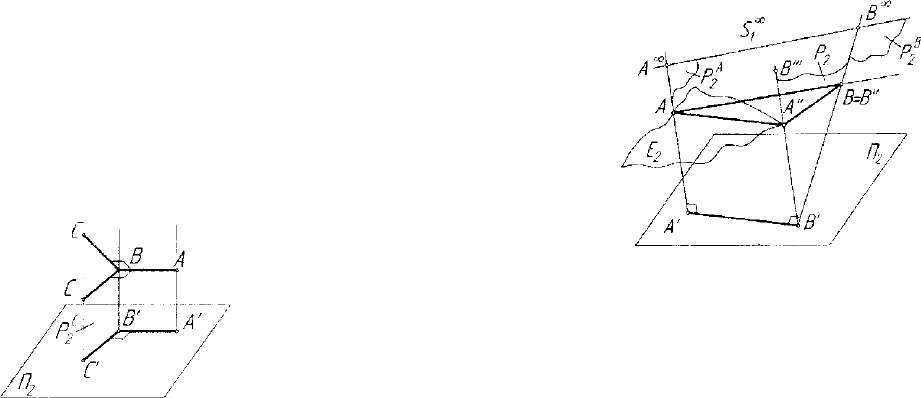
ном проецировании сохраняются все линейные свойства центрально-

го проецирования. Но появляются новые свойства, характерные толь-

ко для параллельного проецирования. К ним относятся нижеследую-

щие свойства.

1. Образами параллельных прямых АВII CD являются парат-

лельньте прямые А'В' II CD'.

2. Сохраняется простое отношение коллинеарных точек

(АВС)^(А'В'С).

3. Если АВIIП

, то \Щ = \А'В\.

Примем эти свойства без доказательств.

Пусть теперь центр S™_

задан так, что (п - 2) различные прямые,

задающие {п-2) направлений, не произвольны, а перпендикулярны

плоскости П

. В этом случае параллельное проецирование становится

ортогональным проецированием. Ортогональное проецирование со-

храняет все свойства параллельного, но появляются некоторые новые

свойства, которые называются метрическими. К ним относятся ниже-

следующие свойства.

1. Проекциями двух ортогональных прямых АВ и ВС являются

ортогональные прямые А'В' и В'С ,

если одна из прямых параллельна

плоскости проекций, а другая ей не

перпендикулярна.

2. Длина отрезка АВ произволь-

ной прямой пространства Е

равна ги-

потенузе прямоугольного треугольни-

ка, один катет которого равен длине

ортогональной проекции А'В' на П

, а

второй - ортогональной проекции

А"В" отрезка АВ на П

, П

1 П

Рис. 1.13. Проекция

прямого угла

П„-2

Рассмотрим доказательство свойства 1 для пространства Е

Пусть ZABC = 90° и пусть АВ IIП

(рис. 1.13). Докажем, что

ZA' В'С =90°. Согласно свойствам параллельных проекций

А'В' II АВ и |/4 7?j=|.<4B|. Вследствие ортогональности проецирования

пространственные линии проекционной связи А'А и В'В ортогональ-

ны П

, поэтому А В В'А' - прямоугольник и А'В' ± ВВ'. Проецирую-

щая 2-плоскость Р

перпендикулярна П

и перпендикулярна А'В' .

А так как АВ II А'В', то Р

перпендикулярна АВ и АВ 1 СС . Пря-

мая ВС проецируется на П

3-плоскостью Р

= <BC,S ™>,

5С В'С . При этом BB'czP

и СС'с Pf

. Поскольку АВ 1 ВС ,

АВ 1 В В', АВ 1 СС , то 451 Pf

. Следовательно, Z^'i?'C = 90°.

Докажем свойство 2 для пространства £

. Пусть Р^ и Pf - про-

ецирующие 2-плоскости точек А, В - концов отрезка АВ

(рис, 1.14). При этом Р$ Ы1

, Р

1П

, А*АА'±П

, В

ВВ'±П

Рис. 1.14. Проекционное представление длины отрезка прямой

Но АЛ' не параллельна В В', так как A

* 5

е0

. Проведем из точки В'

прямую В'В'" II А'А , а через А проведем 2-плоскость Е

IIИ

. Полу-

чим Р

=<ВВ',В'В'

>, Р

±П

, Е

1П

и Е

глР

=А". Имеем:

ортогональная проекция В" точки В на Р

совпадает с В. Можно

заметить, что А'В'А"А - прямоугольник, и что АА"В" - прямоуголь-

ный треугольник с гипотенузой АВ и катетами АА" и А"В". При

этом \АА" \ = \А'В' |. Свойство 2 доказано.

1.6. Размерность множеств элементов евклидова пространства

В геометрии известна формула Грассмана расчета размерности

или параметрического числа линейного объекта:

£%=(п-т)(т+1), (1.1)

где п - размерность объемлющего пространства; т - размерность

плоскости, которая принадлежит объемлющему пространству. Спра-

ведливость формулы (1.1) можно доказать, основываясь на следую-

щих рассуждениях.

Три точки, задающие 2-плоскость, не должны принадлежать од-

ной прямой. Четыре точки, определяющие 3 плоскость, не должны

принадлежать одной 2—плоскости и три точки из них не должны при-

надлежать одной прямой. Пять точек, определяющих 4-плоскость,

не должны принадлежать одной 3-плоскости, четыре точки из них не

должны принадлежать одной 2-плоскости, три точки из них не долж-

ны принадлежать одной прямой. И так далее. В результате получаем,

что (т + 1) точки определяют т плоскость, если никакие q точек из

них, где q<m, не принадлежать одной (д-2)-плоскости. Следова-

тельно, для задания от—плоскости необходимы (т + 1) точки. Каждая

из (т + 1) точек имеет в пространстве Е

параметрическое число,

равное п. Параметрическое число множества (т + 1) точек будет рав-

но п(т + 1). Но каждая из (т + 1) точек в га-плоскости имеет пара-

метрическое число, равное т, а все множество (т + 1) точек - пара-

метрическое число т(т + \). Поэтому, параметрическое число т—

плоскости в пространстве Е

определиться следующим образом:

п(т

+1)

- т(т

+1) =

(п - т)(т +1).

Поскольку формула (1.1) справедлива для евклидова многомер-

ного пространства Е

, то под плоскостью понимается: точка

(О-плоскость), прямая (1-плоскость), обычная плоскость (2-

плоскость), трехмерное пространство (3-плоскость) и т.д. Гиперпло-

скость - это подпространство, размерность которого на единицу

меньше размерности объемлющего (операционного) пространства.

Рассмотрим примеры применения формулы (1.1). Размерность

множества точек в пространстве Е

будет следующей:

£)? = (3 — 0)(0 +1) = 3. То есть точек в пространстве Е

— трехпарамет-

рическое множество, что соответствует известному определению по-

ложения точки в пространстве £

тройкой чисел - координат х, у, z.

Размерность множества прямых линий в пространстве Е

определяет-

ся таким образом: D\ = (3 —1)(1 +1) = 4. Следовательно, прямые линии

в пространстве £, образуют четырехлараметрическое множество.

Размерность множества плоскостей в пространстве Е

имеет сле-

дующее значение: D

=(3-2)(2 + 1) = 3, то есть плоскости этого про-

странства образуют трех параметрическое множество. Объекты с рав-

ными параметрическими числами называют двойственными. Предпо-

ложим, что в пространстве Е„ имеются две плоскости: &-мерная и

(п-к-1) мерная. По формуле (1.1) для первой плоскости можно за-

писать: D„ ~(п-к)(к + Х). Для второй плоскости запишем:

D"~

= {п-п + к + Х)(п-к-\ + Х)~(к + \)(п - к). Следовательно, по

определению, А:-мерная и (и-£-1)-мерная плоскости являются

двойственными объектами пространства Е

Кроме линейных элементов в пространстве Е

существуют и не-

линейные, то есть криволинейные элементы. Рассмотрим из них ал-

гебраические плоские кривые и алгебраические поверхности. Подсчет

параметрических чисел указанных элементов можно выполнить, ис-

пользуя их уравнения. Так, например, общее уравнение кривых в го-

рого порядка (коник) имеет вид: Ах + Ву + Cxy+Dx+Ey+F = 0.

Это уравнение можно привести к виду:

А'х

+В'у

+ Cxy + D'x+E'y + l = Q,

ABC D Е

где А'= - ; В'- —; С'= —; D' = —; Е'- — ; F Ф 0. Очевидно, приня-

F F F F F

тие коэффициентов A',B',C',D',E' переменными приводит к образо-

ванию пятипараметрического множества кривых второго порядка на

плоскости. Обобщая этот факт можно утверждать, что параметриче-

ское число плоской алгебраическое кривой равно числу коэффициен-

тов ее уравнения, уменьшенному на единицу. Плоская алгебраическая

кривая т -го порядка может быть представлена уравнением, которое

запишем построчно с одинаковыми степенями переменных коорди-

нат:

+А

-'у

...

х{т+})

+ A

}

y + ...+ A

+ +

+ Vi)i

x2+

4-i)2*y

^ лузУ

+ А

т1

Х + А

т2У +

+ А

= 0.

(от+1)1

Сумма коэффициентов этого уравнения в парах "симметрично"

расположенных строк равна (т + 2). Исходя из того, что всего число

строк равно (т + 1), можно получить параметрическое число плоской

алгебраической кривой т-го порядка. Оно определится следующим

образом:

(т + 1)(т + 2)

_ т(т + 3)

Аналогичным образом рассуждая, можно получить параметриче-

ское число алгебраической поверхности m-го порядка в пространстве

(т

\){т + 2)(т

3) _

Обобщая рассуждения для алгебраической гиперповерхности

я?-го порядка в пространства Е„, получим формулу параметрическо-

го числа этой поверхности:

т _ (т + \)(т + 2)...(т + п) ,

или в конечном виде:

С1=-,-л(/"+о-1. (1.2)

Если в формуле (1.2) принять п = 2 и т - 2, то получим парамет-

рическое число множества плоских кривых второго порядка на плос-

кости, то есть:

4-i=|'(2+l)(2 + 2)-l=5.

Этот результат подтверждают ранее приведенные рассуждения

относительно определения параметрического числа по уравнению

кривой второго порядка.

Если в формуле (1.2) принять п - 3 и т = 2, то получим:

It, =|-(2

1)(2

2)(2

3)-1

Следовательно, параметрическое число множества алгебраиче-

ских поверхностей второго порядка (квадрик) в пространстве E

рав-

но девяти и поверхность второго порядка определяется девятью па-

раметрами.

Из этого можно заключить следующее. Во-первых, то, что раз-

мерность множества квадрик в пространстве Е

равна девяти означа-

ет, что квадрику общего вида можно задать девятью точками общего

положения. Следовательно, можно найти алгоритм построения любой

точки квадрики по девяти заданным. Можно найти уравнение квадри-

ки, если в уравнение квадрики общего вида подставить координаты

девяти заданных точек и решить систему девяти линейных уравнений

с девятью неизвестными. В качестве неизвестных величин будут вы-

ступать коэффициенты уравнения.

Аналогичный вывод можно сделать и для коник. Но в таком слу-

чае вместо девяти точек в Е

, нужно задать пять точек общего поло-

жения в Е

•

Во-вторых, необходимо иметь в виду существование, так назы-

ваемого собственного пространства алгебраических кривых и поверх-

ностей, в частности коник и квадрик. Собственным пространством

данного геометрического объекта называется пространство мини-

мальной размерности, в котором может быть расположен данный

объект. В этом смысле следует понимать общеизвестный факт, что

коники являются плоскими кривыми. Другими словами, собственное

пространство коник есть плоскость - двумерное пространство. Точно

так же собственным пространством двумерных квадрик является

трехмерное пространство.

Для подтверждения этого вывода поступим следующим образом.

Возьмем на квадрике четыре произвольные точки, не лежащие по три

ни на какой образующей. Через одну пару точек и через другую пару

•1очск проведем две прямые. Эти две прямые будут лежать в трехмер-

ном пространстве, определенном четырьмя выбранными точками.

Можно доказать, что любая точка квадрики будет принадлежать это-

му же трехмерному пространству, а также, что прямая, проведенная

через любые две точки квадрики, тоже будет принадлежать этому же

трехмерному пространству. Следовательно, трехмерное линейное

пространство есть собственное пространство квадрики.

Таким образом, формула (1.2) задает размерность множества ги-

перповерхностей в их собственном пространстве.

(Возникает вопрос, какова будет размерность множества алгеб-

раических поверхностей в пространстве, размерность которого боль-

ше размерности собственного пространства этого множества. Ответ

на него дает теорема: размерность множества в пространстве, раз-

мерность которого больше размерности собственного пространства

этого множества, равна сумме размерности множества в его собст-

венном пространстве и размерности множества собственного про-

странства в данном пространстве. Поэтому для коник будем иметь

размерность их множества в пространстве размерности п>2 в виде

5 + (2 + 1)(/?-2) = 5 + 3(я — 2). Для квадрик при л>3 - в виде

9 + (3 + \)(п - 3) = 9 + 4(п - 3). И так далее.

В третьих. Размерность множества нелинейных геометрических

объектов можно найти конструктивным подсчетом числа параметров

для представителя общего вида этого множества. Поясним это на

примерах. Пусть требуется определить размерность множества коник

на плоскости. В качестве представителя общего вида множества ко-

ник выберем эллипс. Будем рассуждать следующим образом. Чтобы

построить эллипс, необходимо знать координаты его центра точку,

определяемую двумя координатами (два параметра). Кроме этого,

нужно знать направление какой-либо оси - угол между осью эллипса

и осью координат (один параметр). Наконец, нужно задать величины

осей эллипса (два параметра). Таким образом, множество эллипсов на

плоскости пятипараметрично или имеет размерность равную пяти.

Следовательно, размерность множества всех коник на плоскости рав-

на пяти. Однако размерность множества всех парабол на плоскости

равна четырем. Это потому, что парабола не является коникой общего

вида, так как один параметр уже использован на условие касания с

несобственной прямой плоскости. Множество всех окружностей на

плоскости имеет размерность три, так как два параметра потрачены

па условие прохождения коники через две циклические точки плоско-

сти. Множество коник, вырожденных в пары пересекающихся пря-

мых, тоже имеет размерность, равную четырем, так как оно не явля-

ется множеством общего вида.

Аналогичные примеры можно привести для квадрик. К квадри-

кам общего вида относятся трехосные эллипсоиды и эллиптические

гиперболоиды. Для построения трехосного эллипсоида необходимо

знать координаты центра (три параметра), ориентацию любой оси

(два параметра), ориентацию других двух осей относительно первой

(один параметр), длины трех осей (три параметра). В сумме получаем

девять параметров. Эллиптический конус есть вырожденная квадрика.

Множество эллиптических конусов имеет размерность, равную вось-

ми. Действительно, для его задания необходимо иметь эллипс и точ-

ку, не лежащую в плоскости эллипса. Множество эллипсов имеет

размерность равную пяти, а множество точек - трехмерно. Поэтому

множество конусов - восьмимерно. И так далее.

Предположим, что в пространстве Е

ш-плоскость проходит че-

рез q + 1 заданные точки. Для полного определения т -плоскости не-

обходимо дополнительно задать еще (m + l~(q +1) = m-q) точек.

Поэтому параметрическое число т-плоскости в пространстве Е„,

проходящей через заданную q-плоскость, определится следующим

образом:

n(q)

=(n-m)(m-q). (1.3)

1.7. Геометрические условия

/. 7.1. Условия инцидентности

Обобщенным условием инцидентности называется условие, гра-

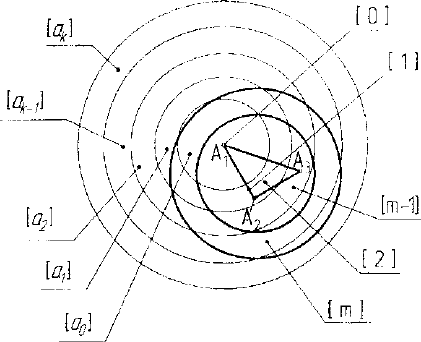
фически пред ставимое так, как показано на рисунке 1.15.

В алгебраической геометрии существует понятие флага. Флаг -

это ряд последовательно вложенных плоскостей разных размерно-

стей.

Предположим, что заданы два флага - полный и неполный. У

полного флага плоскости меньшей размерности принадлежат плоско-

стям большей размерности, то есть 0-плоскость (точка) принадлежит

1-плоскости (прямой), 1-плоскость принадлежит плоскости и т.д. Ус-

ловие последовательной принадлежности для полного флага можно

выразить следующим образом:

101 d 11J с 121 с [3] с... с [т -1] с [т].

Условие принадлежности для неполного флага можно выразить

так:

К-il

[«*]>

где [а

],[а,],[а

],...,[а

кА

],[а

] - плоскости разной размерности, при-

чем разность размерностей соседних плоскостей в ряду последова-

тельных вложений может отличаться от единицы. При этом выполня-

ется инцидентность: [0]с[а

]; [1]с=[а,]; [2]с[а

]; ... ;

[т-Цс[а

_,\; {т\а[а

На рисунке 1.15 имеет место: [0] = ^; Щ-А

, то есть 1-

плоскости принадлежат точки А

,А

; [2] = А

, то есть плоскости

принадлежат точки А

,А

. Для обозначения обобщенного условия

инцидентности и обозначения соответствующих множеств применя-

ется буква е:

т, ml,...,1, 0

,а

,...,щ,а

В приведенной формуле число верхних и нижних индексов рав-

но, а величины т,т-],...,\,0;а

,а

- принимают значения

Рис. 1.15. Геометрическое представление обобщенного

условия инцидентности

чисел натурального ряда. Число т определяет размерность искомого

элемента (т-плоскость), а нижний или нижние индексы - размер-

ность пространства или подпространства, которому принадлежит ис-

комый элемент. Рассмотрим принадлежность (инцидентность) точки

к плоскости в трехмерном пространстве. В этом случае т - флаг со-

стоит из одной точки, то есть т = 0, а а

- флаг состоит из одной

плоскости размерности а

=2. В таком случае получаем е?. Другой

пример. Определим в четырехиараметрическом многообразии прямых

пространства Е

те прямые, которые пересекают заданную прямую. В

этом случае получаем, что т = 1 и т-флаг состоит из прямой и точки,

ей принадлежащей, а а^-флаг состоит из трехмерного пространства и

прямой в нем. Следовательно, прямая флага принадлежит простран-

ству Е

, а ее точка принадлежит заданной в этом пространстве пря-

мой. Таким образом, получаем е

\\ Если т-флаг состоит из плоско-

сти, инцидентной ей прямой и инцидентной этой прямой точки, а а

флаг состоит из пространства Е

, плоскости и точки, то условием ин-

цидентности е

\ определяется множество плоскостей пространства

, проходящих через заданную точку, то есть связку.

Приведем простейшие условия инцидентности для точек, прямых

и плоскостей пространства Е

. Для точек это следующие условия:

0 0 0 0 о

,е

, где е§- условие совпадения точки пространства с задан-

ной точкой; ef- условие принадлежности точки заданной прямой

пространства; е^

условие принадлежности точки заданной плоско-

сти пространства; условие принадлежности точки пространству

Для прямых линий имеют место следующие условия инцидент-

ности: e[§;e

j/,e

j\elf

;el'°-,el'2. Расшифруем некоторые из этих усло-

вий.

Условие

определяет пучок прямых,

связку прямых,

®— поле прямых.

•л- •• 2,1,0 2,1,0 2,1,0 2.1,0 лг„

Для плоскостей имеют место условия: ^'iJ^AO^.i.o^y.o-

Уо

ловие е

'\'® определяет пучок плоскостей, условие ej'i'o определяет

совпадение плоскости пространства с заданной в нем плоскостью.

Обобщенное условие инцидентности характеризуется размерно-

стью, которая определяется по формуле [5]:

.№^!S±J)_f;

„ (,.4)

где п - размерность объемлющею пространства; т - размерность

плоскости, которая удовлетворяет обобщенному условию инцидент-

ности; а, - "нижние" коэффициенты обобщенного условия инцидент-

ности.

Определим на основе формулы (1.4) размерности условий инци-

дентности для точки, прямой и плоскости прострапства Е

(e°) = 2; QJ&) = b О#

°) = 3;

(Ч?) =1; а

(4;°о) = 2; QoM") = 2; = 3; О* (eft) = 4;

Qo6(4$)

= i;

QoMii)

з.

Рассмотрим подробное получение некоторых из указанных ре-

зультатов вычислений по формуле (1.4):

1.7.2. Аффинные условия

Для рассмотрения аффинных условий требуется введение поня-

тия несобственных (бесконечно удаленных) элементов. Прямая линия

а дополняется несобственной точкой А

, плоскость В- несобствен-

ной прямой b о» пространство Е

— несобственной плоскостью А

пространство Е„ - несобственной гиперплоскостью /Г," ".Тома па-

раллельными будем считать такие две прямые, точка пересечения ко-

торых принадлежит несобственной прямой плоскости этих прямых.

Прямая и плоскость параллельны, если их точка пересечения принад-

лежит несобственной прямой этой плоскости. Две плоскости парал-

лельны, если их линия пересечения принадлежит несобственной

плоскости А,, пространства Е

. Понятие "параллельность" является

понятием аффинной геометрии. Не всякие два линейных элемента

пространства могут быть параллельными. Например, в общем случае

две прямые пространства Е

являются скрещивающимися, также как

прямая и плоскость в четырехмерном пространстве. Следовательно,

параллельность двух линейных элементов пространства возможна

при выполнении двух условий: линейные элементы должны пересе-

каться в этом пространстве, элемент их пересечения должен быть не-

собственным. Предположим, что в пространстве Е

пересекаются два

подпространства размерностей т и q. Каждое из них определяется

множеством (т + \) и (q + \) точек соответственно. Пусть их общая

часть пересечения будет пространством размерности s , определяе-

мом (s+1) точкой. В таком случае подпространство размерности т,

определяемом (т +1) независимыми точками, кроме (s +1) точек со-

держит еще (т - s) независимых точек, а подпространство размерно-

сти q, определяемое (q + \) независимыми точками, кроме (.? + !) со-

держит еще (q — s) независимых точек. Суммарное число независи-

мых точек (s +1 + т — s + q — s) равно числу (п + \) независимых то-

чек, определяющих объемлющее пространство п, то сеть

n + \-s + \ + m-s + q- s. Таким образом, получаем формулу:

s - т + q - п, которая позволяет определять размерность простран-

ства пересечения. Из этой формулы следует, что две прямые в про-

странстве Е

в общем случае действительно не пересекаются:

+ 1-3 = -1.

Две гиперплоскости в пространстве Е

пересекаются по плоско-

сти, поскольку 3 + 3-4 = 2. Если эта плоскость несобственная, то две

гиперплоскости параллельны в этом пространстве. Гиперплоскость и

плоскость в пространстве Е

пересекаются по прямой линии, по-

скольку 3 + 2-4 = 1. Если эта прямая несобственная, то названные

элементы параллельны в рассматриваемом пространстве. Исходя из

числа независимых точек, определяющих несобственный элемент пе-

ресечения, можно сформулировать условие параллельности исходных

элементов. Так в последнем случае несобственная прямая определяет-

ся двумя точками. Поэтому гиперплоскость и плоскость в простран-

стве Е

параллельны, если две пересекающиеся прямые плоскости

параллельны каким-либо двум прямым гиперплоскости.

Условия параллельности одних и тех же элементов, но принад-

лежащих разным объемлющим пространствам, существенно разли-

чаются. Например, две плоскости в пространстве Е

пересекаются в

точке (2 + 2 — 4 = 0), следовательно, они будут параллельными, если

прямая в одной плоскости будет параллельна какой-либо прямой в

другой плоскости. В пространстве Е

две плоскости пересекаются по

прямой, так как 2 + 2-3 = 1. Если она несобственная, то получаем из-

вестный в школьном курсе стереометрии признак параллельности

этих плоскостей. Различие параллельностей одних и тех же элементов

в разных пространствах характеризуется степенью параллельности,

которая определяется формулой [16]:

£+1 П ч~\

Рц= . С

)

где к — размерность общего несобственного элемента двух парал-

лельных элементов (прямых, плоскостей, гиперплоскостей), т и q -

размерности параллельных элементов, при этом m<q. Рассмотрим

применение этой формулы. Для плоскостей пространства Е

получа-

ем: Рц~~^

^- Следовательно, две плоскости пространства Е

вполне параллельны. Те же две плоскости в пространстве Е

имеют

степень параллельности, равную Рц

^~^-

\- Следовательно, две

плоскости в пространстве Е

полупараллельны. Две гиперплоскости

в пространстве Е

обладают степенью параллельности, равной

зз

Рц = —у- = 1, то есть гиперплоскости в этом пространстве вполне па-

раллельны.

Для определения размерности условия параллельности существу-

ет формула [4]:

Qjj= p

-m(n-m-q + рц-т). (1.6)

Согласно формуле размерность условия параллельности прямой

и плоскости в пространстве £

определится следующим образом:

=l-J(3-l-2 + l-l) = l.

Размерность условия параллельности двух плоскостей в про-

странстве Е

определится так: = 1 • 2(3 - 2 - 2+1 • 2) = 2.

Условие параллельности подпространств Е

и Е , т < q, можно

сформулировать следующим образом. Подпространства Е

и Е

пространства Е

будут вполне параллельны, если одно из них можно

перенести в другое параллельным переносом. Или, если для любых

т прямых пространства Е

, проходящих через одну точку, в про-

странстве Е найдутся т параллельных им прямых, не обязательно

проходящих через одну точку, то подпространства Е

и Е вполне

параллельны. При этом их линейным расширением будет подпро-

странство £ , с: Е

, размерности (q + l).

Если же для любых т прямых пространства Е

, проходящих

через одну точку, в пространстве Е найдутся (/и-1) нарачлельных

им прямых, то пространства Е

и Е будут не вполне параллельны.

П ^

W_1

ТА

Степень их параллельности будет равна . Их линейным расши-

рением будет подпространство E

q+2

<zz Е

. И так далее.

Если же для любых т прямых пространства Е

в пространстве

не найдется ни одной параллельной им прямой, то это означает,

что пространства Е

и Е

не параллельны. Степень их параллельно-

сти равна нулю. Их линейным расширением будет подпространство

1.7.3. Условия перпендикулярности

В трехмерном пространстве £

через произвольную точку О не-

которой прямой можно провести плоскость А, перпендикулярную

данной прямой. Все прямые этой плоскости, проходящие через точку

О, то есть пучок прямых (0), перпендикулярны данной прямой. В

пучке (0) прямых всегда найдутся две взаимноперпендикулярные

прямые. Следовательно, в любой точке пространства Е

существует

тройка взаимно перпендикулярных прямых. В пространстве Е

на

некоторой его прямой выберем точку О. Проведем через эту точку

все возможные прямые, плоскости и 3 -плоскости, перпендикулярные

исходной прямой. Параметрическое число прямой пространства £

проходящей через точку О, по формуле (1.3) равно:

(0)

= (4 -1)(1 - 0) = 3. Введение условия перпендикулярности этой

прямой к заданной прямой уменьшает на единицу ее параметрическое

число. Поэтому множество прямых пространства £

, проходящих че-

рез точку О перпендикулярно заданной прямой, двухпараметрично,

то есть образует связку. В пучке прямых этой связки существует' две

взаимноперпендикулярные прямые, перпендикулярные заданной

прямой. В связке прямых существует прямая вне плоскости этих вза-

имноперпендикулярных прямых, перпендикулярная этой плоскости.

То есть, через точку О заданной прямой пространства £

проходит

тройка взаимноиерпендикулярных прямых, перпендикулярных задан-

ной прямой. Эта тройка прямых определяет подпространство £

, ко-

торое проходит через точку О перпендикулярно заданной прямой.

Очевидно, все прямые подпространства £

, проходящие через точку

О, также перпендикулярны заданной прямой. Обобщая на простран-

ство Е„, можно утверждать о том, что через точку О заданной пря-

мой этого пространства проходит (и —1) независимых прямых, пер-

пендикулярных данной прямой, при этом никакая тройка таких пря-

мых не принадлежит одной плоскости. Следовательно, через точку О

заданной прямой пространства Е

проходит единственное подпро-

странство Е

,, перпендикулярное этой прямой.

Очевидно, обратное утверждение также имеет место: через точку

О подпространства £„_, в пространстве Е„ проходит единственная

прямая пространства, перпендикулярная к подпространству Е

, то

есть перпендикулярная к его 1-плоскости, плоскости, 3 -плоскости,

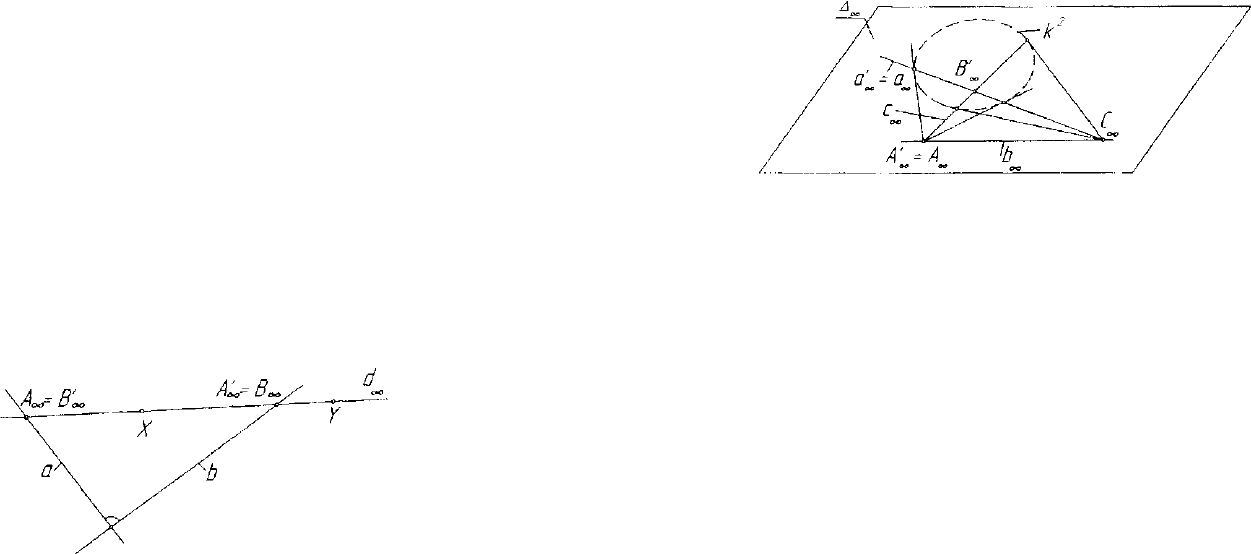
... , проходящих через точку О. Таким образом, через произвольную

точку пространства Е

проходят п взаимноперпендикулярных пря-

мых. Рассмотрим подробнее свойство перпендикулярности этих п

прямых.

Выберем из п взаимноперпендикулярных прямых q прямых.

Они определяют q -плоскость E

. Тогда любая прямая q -плоскости

, проходящая через точку О, будет перпендикулярна оставшимся

n-q прямым, следовательно, перпендикулярна (и-^-плоскости

определяемой (n-q) прямыми и любой прямой (n-q)-

плоскости Е , проходящей через точку О.

(/-плоскость Е и (п-q)—плоскость E

, пересекающиеся в

точке О, на основании вышеизложенною, характеризуются тем, что

любая прямая одной из них, проходящая через точку О, перпендику-

лярна всем прямым другой, также проходящим через точку О. Такие

две су-плоскость Е и (л — ^)—плоскость E

, или два подпростран-

ства Е и Е

. называются вполне перпендикулярными.

Строгое определение понятия перпендикулярности может быть

дано на основе абсолютов расширенных плоскости и пространства,

которые дополнены несобственными элементами. Абсолют плоскости

представляет собой несобственную прямую d

этой плоскости с ус-

тановленной па ней эллиптической (абсолютной) инволюцией точек,

определяемой парой циклических (мнимых) точек X и Y пересечения

окружности этой плоскости с прямой d,

(рис. 1.16).

Рис. 1.16. Абсолют расширенной евклидовой плоскости

С проективной точки зрения, две прямые а и Ь в плоскости

перпендикулярны, если их точки пересечения 4»

являются со-

ответственными в абсолютной инволюции: А

++А'

, В

<->В'

А'

= В

, В^=А

[10,16,37].

Абсолютом расширенного пространства £

называется мнимая

окружность к

в несобственной плоскости А

и полярное соответст-

вие в плоскости А,„, устанавливаемое этой окружностью (рис. 1.17).

Мнимая окружность к

представляется как линия пересечения сферы

пространства Е

я его плоскости А«>-

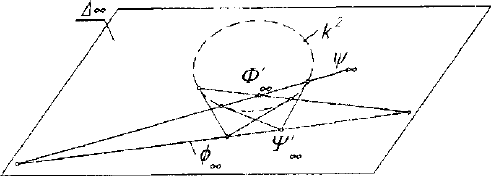
Рис. 1.17. Интерпретации перпендикулярности

прямой и плоскости

В проективной интерпретации прямая а и плоскость О будут

перпендикулярными, если точка А^= а(\А

я прямая а

~ Q Г]А

1Х1

соответственны в полярном соответствии относительно мнимой ок-

ружности к

<г>

о ж, а

<->

сс

, а

= а

, А

сг

. = А

Две плоскости Ф и W в пространстве Е

будут перпендикуляр-

ными, если образ А'^ несобственной прямой а

= Фр|4» в полярном

соответствии относительно мнимой окружности к

принадлежит не-

собственной прямой b

= WC\A

. Или же: обр*аз В'^ несобственной

прямой Ь

— !РП4»

8 том же

полярном соответствии принадлежит не-

собственной прямой а

= ФГ)4» .

Выполним обобщение понятия перпендикулярности на простран-

ство Е

. Абсолютом этого пространства является мнимая (п — 2)-

сфера К

, полученная в пересечении гиперсферы К пространства

с его несобственной гиперплоскостью А

, и полярное соответст-

вие, устанавливаемое («-2)-сферой К

в гиперплоскости 4

. В

этом полярном соответствии точке соответствует (п -2)-плоскость

£„°°2> прямой линии Ej

соответствует («-3)-плоскость Е™_

, ... , т

-плоскости Е™ соответствует (п -т -2) -плоскость Е™_

т 2

Предположим, что в расширенном евклидовом пространстве Е

заданы т-плоскость Ф

и q-плоскость 4

, при этом m>q. Пусть

их общей частью будет р-илоскость 1

, определяемая (р + 1) неза-

висимыми точками. В таком случае /и плоскость Ф

кроме (р + 1)

точек будет содержать (т - р) независимых точек, a q -плоскость У

кроме (р + 1) точек будет содержать еще (q-р) независимых точек.

Следовательно, общее число независимых точек будет равно

р + \ + т-p + q-p = m + q-р + \, и оно равно 0 + 1) независимых

точек, определяющих пространство Е

. В итоге получаем формулу:

p = m + q-n. (1.7)

w-плоскость Ф

и (/-плоскость !? в пересечении с гиперпло-

скостью A

образуют элементы: Ф

Г\Л«,= <&Z-\ \ ^Л\Л^=^_

. В по-

лярпом соответствии относительно мнимой (я-2)-сферы К

в ги-

перплоскости

А,, (т-1)

плоскости

Ф'°.-\

соответствует (п-т-1)

плоскость Ф*4„^у.2~Ф2-т-[- Очевидно, в общем случае элементы

Ф^-

'Уд'-]* принадлежащие несобственной гиперплоскости A

между собой не пересекаются, поскольку согласно формуле (1.7) по-

лучаем: $n-m-$ + (q-])-(n-Y)] = ~m + q-\<Q. Это говорит о

том, что исходные /и-плоскость Ф

и плоскость W не перпен-

дикулярны в пространстве Е

. Если же элементы Ф"

-\ и пе-

ресекаются по г-плоскости Е?, то они считаются вполне перпенди-

кулярными и степень их перпендикулярности определяется по фор-

муле [16]:

г +

Р. = (1.8)

где q - меньшая из размерностей т и q исходных плоскостей Ф и

Рассмотрим несколько примеров. Две прямые а и Ъ в плоскости

при условии А'

= В

или В'

= А

(рис. 1.16) имеют степень

перпендикулярности, равную р

= —j—= 1, то есть они вполне пер-

пендикулярны. Прямая а и плоскость в в пространстве Е

при усло-

вии а'

= а

или /г" =4* (рис. 1.17) имеют степень перпендикуляр-

ности, равную р

=^у-^- = 1, то есть они также вполше перпендику-

лярны. Две плоскости Ф и W пространства Е

при условии Ф' е <//

или У,» еф

, где ф

<в

=ФГ\Л

а>

, ^

=!Р

П^« (рис. 1.18) имеют степень

0 + 1 1

перпендикулярности, равную/?

== -, то есть две плоскости

этого пространства лишь полуперпендикулярны.

Рис. 1.18. Интерпретации перпендикулярности двух плоскостей

Для определения размерности условия перпендикулярности при-

меняется формула [4]:

-q(m-q + p

-q), (1.9)

в которой т и q - размерности взаимно перпендикулярных элемен-

тов (m>q). Размерность условия перпендикулярности двух прямых в

плоскости Е

в соответствии с формулой (1.9) равна:

=1-1(1 -1 + 1-1) = 1. Размерность условия перпендикулярности

прямой и плоскости в пространстве Е

равна: Q

-1 • 1(2 -1 +1 • 1) = 2.

Размерность условия перпендикулярности двух плоскостей в про-

странстве Е

равна: Q

- — • 2(2 - 2 + — • 2) = 1.